Динамическое программирование.ppt
- Количество слайдов: 51
 Динамическое программирование
Динамическое программирование
 Содержание • • • Основные понятия Немного истории Критерии использования Подходы к решению задач в ДП Задача об оптимального пути – – «Фишки» «Черепашка» «Штраф» «Робот»
Содержание • • • Основные понятия Немного истории Критерии использования Подходы к решению задач в ДП Задача об оптимального пути – – «Фишки» «Черепашка» «Штраф» «Робот»
 Содержание (продолжение) • Задача о наибольшей общей подпоследовательности • Задача о загрузке (о распределении ресурсов – Задача о загрузке судна – Задача о рюкзаке • Задачи для самостоятельного решения • Источники
Содержание (продолжение) • Задача о наибольшей общей подпоследовательности • Задача о загрузке (о распределении ресурсов – Задача о загрузке судна – Задача о рюкзаке • Задачи для самостоятельного решения • Источники
 Основные понятия Динамическое программирование (ДП) — это метод решения задач с оптимальной подструктурой и перекрывающимися подзадачами, который намного эффективнее, чем решение «в лоб»
Основные понятия Динамическое программирование (ДП) — это метод решения задач с оптимальной подструктурой и перекрывающимися подзадачами, который намного эффективнее, чем решение «в лоб»
 Основные понятия (продолжение) • Оптимальная подструктура в динамическом программировании означает, что оптимальное решении подзадач меньшего размера может быть использовано для решения исходной задачи. Подзадачи решаются делением их на подзадачи ещё меньшего размера и т. д. , пока не дойдем до тривиального случая задачи, решаемой за константное время (ответ можно сказать сразу).
Основные понятия (продолжение) • Оптимальная подструктура в динамическом программировании означает, что оптимальное решении подзадач меньшего размера может быть использовано для решения исходной задачи. Подзадачи решаются делением их на подзадачи ещё меньшего размера и т. д. , пока не дойдем до тривиального случая задачи, решаемой за константное время (ответ можно сказать сразу).
 Основные понятия (продолжение) • Перекрывающиеся подзадачи в динамическом программировании означают подзадачи, которые используются для решения некоторого количества задач (не одной) большего размера (то есть мы несколько раз проделываем одно и то же). Ярким примером является вычисление последовательности Фибоначчи
Основные понятия (продолжение) • Перекрывающиеся подзадачи в динамическом программировании означают подзадачи, которые используются для решения некоторого количества задач (не одной) большего размера (то есть мы несколько раз проделываем одно и то же). Ярким примером является вычисление последовательности Фибоначчи
 Основные понятия (продолжение) Мы будем сохранять решения подзадач, которые мы уже решали, и когда нам снова потребуется решение подзадачи, мы вместо того, чтобы вычислять его заново, просто достанем его из памяти. Этот подход называется кэширование. Можно проделывать и дальнейшие оптимизации — например, если мы точно уверены, что решение подзадачи нам больше не потребуется, можно выкинуть его из памяти, освободив её для других нужд, или если процессор простаивает и мы знаем, что решение некоторых, ещё не посчитанных подзадач, нам понадобится в дальнейшем, мы можем решить их заранее.
Основные понятия (продолжение) Мы будем сохранять решения подзадач, которые мы уже решали, и когда нам снова потребуется решение подзадачи, мы вместо того, чтобы вычислять его заново, просто достанем его из памяти. Этот подход называется кэширование. Можно проделывать и дальнейшие оптимизации — например, если мы точно уверены, что решение подзадачи нам больше не потребуется, можно выкинуть его из памяти, освободив её для других нужд, или если процессор простаивает и мы знаем, что решение некоторых, ещё не посчитанных подзадач, нам понадобится в дальнейшем, мы можем решить их заранее.
 Немного истории Словосочетание динамическое программирование впервые было использовано в 1940 -х годах Р. Беллманом для описания процесса нахождения решения задачи, где ответ на одну задачу может быть получен только после решения задачи, «предшествующей» ей. В 1953 г. он уточнил это определение до современного. Первоначально эта область была основана, как системный анализ и инжиниринг, которая была признана IEEE. Вклад Беллмана в динамическое программирование был увековечен в названии уравнения Беллмана, центрального результата теории динамического программирования, который переформулирует оптимизационную задачу в рекурсивной форме.
Немного истории Словосочетание динамическое программирование впервые было использовано в 1940 -х годах Р. Беллманом для описания процесса нахождения решения задачи, где ответ на одну задачу может быть получен только после решения задачи, «предшествующей» ей. В 1953 г. он уточнил это определение до современного. Первоначально эта область была основана, как системный анализ и инжиниринг, которая была признана IEEE. Вклад Беллмана в динамическое программирование был увековечен в названии уравнения Беллмана, центрального результата теории динамического программирования, который переформулирует оптимизационную задачу в рекурсивной форме.
 Критерии использования Динамическое программирование пользуется следующими свойствами задачи: • Перекрывающиеся подзадачи. • Оптимальная подструктура. • Возможность запоминания решения часто встречающихся подзадач.
Критерии использования Динамическое программирование пользуется следующими свойствами задачи: • Перекрывающиеся подзадачи. • Оптимальная подструктура. • Возможность запоминания решения часто встречающихся подзадач.
 Подходы к решению задач в ДП • Нисходящее ДП: задача разбивается на подзадачи меньшего размера, они решаются и затем комбинируются для решения исходной задачи. Используется запоминание для решений часто встречающихся подзадач. • Восходящее ДП: Все подзадачи, которые впоследствии понадобятся для решения исходной задачи просчитываются заранее и затем используются для построения решения исходной задачи. Этот способ лучше нисходящего ДП в смысле размера необходимого стека и количества вызова функций, но иногда бывает нелегко заранее выяснить решение каких подзадач нам потребуется в дальнейшем.
Подходы к решению задач в ДП • Нисходящее ДП: задача разбивается на подзадачи меньшего размера, они решаются и затем комбинируются для решения исходной задачи. Используется запоминание для решений часто встречающихся подзадач. • Восходящее ДП: Все подзадачи, которые впоследствии понадобятся для решения исходной задачи просчитываются заранее и затем используются для построения решения исходной задачи. Этот способ лучше нисходящего ДП в смысле размера необходимого стека и количества вызова функций, но иногда бывает нелегко заранее выяснить решение каких подзадач нам потребуется в дальнейшем.
 Задача об оптимального пути «Фишка» Фишка может двигаться по полю длины N только вперед. Длина хода фишки не более K. Найти число различных путей, по которым фишка может пройти поле от начала до конца. Пример. N=3, K=2 Возможные пути: 1, 1, 1 1, 2 2, 1 Ответ: 3.
Задача об оптимального пути «Фишка» Фишка может двигаться по полю длины N только вперед. Длина хода фишки не более K. Найти число различных путей, по которым фишка может пройти поле от начала до конца. Пример. N=3, K=2 Возможные пути: 1, 1, 1 1, 2 2, 1 Ответ: 3.
 «Фишка» (продолжение) Решение задачи Очевидное решение задачи предполагает разложение числа N на всевозможные суммы таким образом, чтобы каждое слагаемое в сумме не превосходило k. Очевидно, что таких разложений очень много, особенно если учитывать, порядок слагаемых в разложении существенен, так как он соответствует различной последовательности ходов фишки.
«Фишка» (продолжение) Решение задачи Очевидное решение задачи предполагает разложение числа N на всевозможные суммы таким образом, чтобы каждое слагаемое в сумме не превосходило k. Очевидно, что таких разложений очень много, особенно если учитывать, порядок слагаемых в разложении существенен, так как он соответствует различной последовательности ходов фишки.
 «Фишка» (продолжение) • Обозначим через S(i) количество различных путей, по которым фишка может пройти поле от начала до позиции с номером i. Предположим теперь, что для любого j от 1 до i известны значения величин S(j). Задача состоит в определении правила вычисления значения S(i+1), используя значения известных величин. Легко заметить, что в позицию с номером i+1 фишка может попасть из позиций i, i-1, . . . , i-k. Следовательно, S(i+1)=S(i)+S(i-1)+. . . +S(i-k).
«Фишка» (продолжение) • Обозначим через S(i) количество различных путей, по которым фишка может пройти поле от начала до позиции с номером i. Предположим теперь, что для любого j от 1 до i известны значения величин S(j). Задача состоит в определении правила вычисления значения S(i+1), используя значения известных величин. Легко заметить, что в позицию с номером i+1 фишка может попасть из позиций i, i-1, . . . , i-k. Следовательно, S(i+1)=S(i)+S(i-1)+. . . +S(i-k).
 «Фишка» (продолжение) • Таким образом, вычисляя последовательно значения величин S(1), S(2), . . . , S(N) по описанному выше правилу, получаем значение S(N), которое и указывает общее количество различных путей, по которым фишка может пройти поле от начала до позиции с номером N.
«Фишка» (продолжение) • Таким образом, вычисляя последовательно значения величин S(1), S(2), . . . , S(N) по описанному выше правилу, получаем значение S(N), которое и указывает общее количество различных путей, по которым фишка может пройти поле от начала до позиции с номером N.
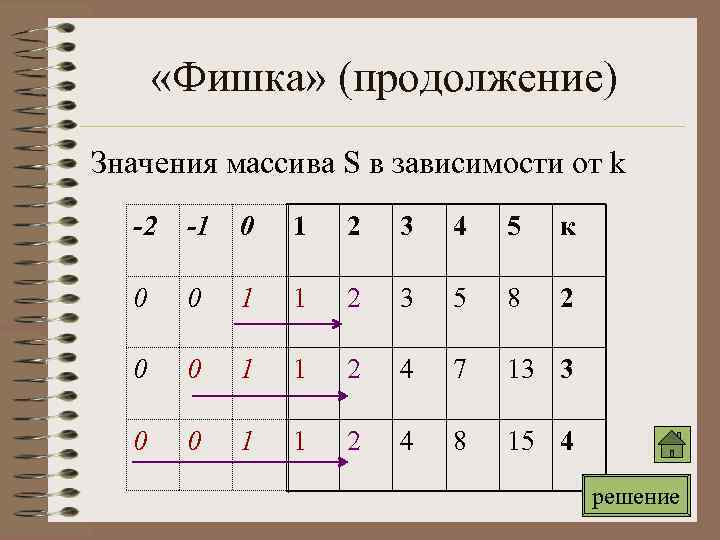 «Фишка» (продолжение) Значения массива S в зависимости от k -2 -1 0 1 2 3 4 5 к 0 0 1 1 2 3 5 8 2 0 0 1 1 2 4 7 13 3 0 0 1 1 2 4 8 15 4 решение
«Фишка» (продолжение) Значения массива S в зависимости от k -2 -1 0 1 2 3 4 5 к 0 0 1 1 2 3 5 8 2 0 0 1 1 2 4 7 13 3 0 0 1 1 2 4 8 15 4 решение
 «Черепашка» В таблице размером N*N, где N<13, клетки заполнены случайным образом цифрами от 0 до 9. Предложить Черепашке алгоритм, позволяющий найти маршрут из клетки (1, 1) в клетку (N, N) и удовлетворяющий следующим условиям: 1 любые две последовательные клетки в маршруте имеют общую сторону; 2. количество клеток маршрута минимально; 3. сумма цифр в клетках маршрута максимальна.
«Черепашка» В таблице размером N*N, где N<13, клетки заполнены случайным образом цифрами от 0 до 9. Предложить Черепашке алгоритм, позволяющий найти маршрут из клетки (1, 1) в клетку (N, N) и удовлетворяющий следующим условиям: 1 любые две последовательные клетки в маршруте имеют общую сторону; 2. количество клеток маршрута минимально; 3. сумма цифр в клетках маршрута максимальна.
 «Черепашка» (продолжение) Будем искать наилучшие пути, идущие из клетки (1, 1) во все остальные клетки таблицы, в частности и в клетку (N, N). Для этого в некоторой вспомогательной таблице B того же размера, что и А, будем отмечать суммы цифр оптимальных путей, ведущих в соответствующие клетки. Так в клетке(1, 1) таблицы В окажется число А(1, 1), потому что путь, ведущий в нее , состоит из одной клетки. Так же легко заполняются клетки (1, 2) и (2, 1) таблицы В. В них тоже ведут единственные пути. и суммы цифр вдоль них равны А(1, 1)+А(1, 2) и А(1, 1)+А(2, 1) соответственно.
«Черепашка» (продолжение) Будем искать наилучшие пути, идущие из клетки (1, 1) во все остальные клетки таблицы, в частности и в клетку (N, N). Для этого в некоторой вспомогательной таблице B того же размера, что и А, будем отмечать суммы цифр оптимальных путей, ведущих в соответствующие клетки. Так в клетке(1, 1) таблицы В окажется число А(1, 1), потому что путь, ведущий в нее , состоит из одной клетки. Так же легко заполняются клетки (1, 2) и (2, 1) таблицы В. В них тоже ведут единственные пути. и суммы цифр вдоль них равны А(1, 1)+А(1, 2) и А(1, 1)+А(2, 1) соответственно.
 «Черепашка» (продолжение) Поясним сказанное на конкретном примере. Пусть таблица А размером 5*5 имеет вид, представленный на рис. 2. Нумерация клеток идет от левого верхнего угла. Проследим за заполнением таблицы В. О клетках (1, 2) и (2, 1) уже говорилось. Чтобы заполнить клетку (2, 2), заметим, что в нее можно попасть либо из клетки (1, 2), либо из клетки (2, 1). Следовательно, в клетку (2, 2) таблицы В надо записать либо число В(1, 2)+А(2, 2), либо число В(2, 1)+А(2, 2), в зависимости от того, какое из них больше. Заполнение остальных клеток таблицы В аналогично.
«Черепашка» (продолжение) Поясним сказанное на конкретном примере. Пусть таблица А размером 5*5 имеет вид, представленный на рис. 2. Нумерация клеток идет от левого верхнего угла. Проследим за заполнением таблицы В. О клетках (1, 2) и (2, 1) уже говорилось. Чтобы заполнить клетку (2, 2), заметим, что в нее можно попасть либо из клетки (1, 2), либо из клетки (2, 1). Следовательно, в клетку (2, 2) таблицы В надо записать либо число В(1, 2)+А(2, 2), либо число В(2, 1)+А(2, 2), в зависимости от того, какое из них больше. Заполнение остальных клеток таблицы В аналогично.
 «Черепашка» (продолжение) Если путь, ведущий в эту клетку один, то в клетку вписывается сумма цифр вдоль этого пути. Такими клетками являются клетки вида (1, J) и (J, 1). Если же в клетку (I, J) можно попасть из клеток для которых подсчитаны значения В, то необходимо выбрать М=мах{B(I, J-1), B(I-1, J} и записать в клетку B(I, J) число М+А(I, J).
«Черепашка» (продолжение) Если путь, ведущий в эту клетку один, то в клетку вписывается сумма цифр вдоль этого пути. Такими клетками являются клетки вида (1, J) и (J, 1). Если же в клетку (I, J) можно попасть из клеток для которых подсчитаны значения В, то необходимо выбрать М=мах{B(I, J-1), B(I-1, J} и записать в клетку B(I, J) число М+А(I, J).
 «Черепашка» (продолжение)
«Черепашка» (продолжение)
 «Черепашка» (продолжение) Клетку B(I, J) соединим чертой с той клеткой, где был достигнут максимум М. Для нахождения искомого маршрута достаточно пройти из клетки (N, N) в клетку (1, 1) по черточкам. решение
«Черепашка» (продолжение) Клетку B(I, J) соединим чертой с той клеткой, где был достигнут максимум М. Для нахождения искомого маршрута достаточно пройти из клетки (N, N) в клетку (1, 1) по черточкам. решение
 «Штраф» Задана матрица натуральных чисел A(n, m). За каждый проход через клетку (i, j) взымается штраф A(i, j). Необходимо минимизировать штраф и а) Пройти из какой-либо клетки 1 -ой строки в n-ую строчку, при этом из текущей клетки можно перейти 1) в любую из 3 -х соседних, стоящих в стpоке с номеpом на 1 -цу большем; 2) в любую из 8 соседних клеток; б) Реализовать пункт a) для перехода из клетки (1, 1) в (n, m).
«Штраф» Задана матрица натуральных чисел A(n, m). За каждый проход через клетку (i, j) взымается штраф A(i, j). Необходимо минимизировать штраф и а) Пройти из какой-либо клетки 1 -ой строки в n-ую строчку, при этом из текущей клетки можно перейти 1) в любую из 3 -х соседних, стоящих в стpоке с номеpом на 1 -цу большем; 2) в любую из 8 соседних клеток; б) Реализовать пункт a) для перехода из клетки (1, 1) в (n, m).
![«Штраф» (продолжение) для i от 1 до n Штраф[i, 1]: =A[i, 1] для «Штраф» (продолжение) для i от 1 до n Штраф[i, 1]: =A[i, 1] для](https://present5.com/presentation/3/102677620_388896621.pdf-img/102677620_388896621.pdf-23.jpg) «Штраф» (продолжение) для i от 1 до n Штраф[i, 1]: =A[i, 1] для i от 2 до n для j от 1 до m нц Штраф[i, j]: =Штраф[i-1, j]+A[i, j]; если j>1 и Штраф[i, j] < Штраф[i-1, j 1]+A[i, j]; то Штраф[i, j]: =Штраф[i-1, j 1]+A[i, j]; если j
«Штраф» (продолжение) для i от 1 до n Штраф[i, 1]: =A[i, 1] для i от 2 до n для j от 1 до m нц Штраф[i, j]: =Штраф[i-1, j]+A[i, j]; если j>1 и Штраф[i, j] < Штраф[i-1, j 1]+A[i, j]; то Штраф[i, j]: =Штраф[i-1, j 1]+A[i, j]; если j
 «Робот» • • • В исследовательской лаборатории фирмы Robots&Co разработали новую модель робота. Главной особенностью данной модели робота является то, что он работает по заранее заданной программе, в которой могут присутствовать команды: сделать шаг на Юг, на Север, на Восток или на Запад. Робот исполняет программу строго последовательно и, дойдя до конца программы, останавливается. Специалисты из Robots&Co заинтересовались вопросом, сколько существует различных программ, состоящих из K инструкций, таких, что робот, выйдя из начала координат, придет в точку с координатами (X, Y). Оси координат располагаются параллельно сторонам света, и единица измерения, соответствует одному шагу робота. Напишите программу, которая дает ответ на этот вопрос. Формат входных данных Во входном файле находятся три числа K, X и Y (0 <= K <= 16, |X|, |Y| <= 16), разделенные пробелами. Формат выходных данных В выходной файл ваша программа должна поместить одно число — количество программ для робота.
«Робот» • • • В исследовательской лаборатории фирмы Robots&Co разработали новую модель робота. Главной особенностью данной модели робота является то, что он работает по заранее заданной программе, в которой могут присутствовать команды: сделать шаг на Юг, на Север, на Восток или на Запад. Робот исполняет программу строго последовательно и, дойдя до конца программы, останавливается. Специалисты из Robots&Co заинтересовались вопросом, сколько существует различных программ, состоящих из K инструкций, таких, что робот, выйдя из начала координат, придет в точку с координатами (X, Y). Оси координат располагаются параллельно сторонам света, и единица измерения, соответствует одному шагу робота. Напишите программу, которая дает ответ на этот вопрос. Формат входных данных Во входном файле находятся три числа K, X и Y (0 <= K <= 16, |X|, |Y| <= 16), разделенные пробелами. Формат выходных данных В выходной файл ваша программа должна поместить одно число — количество программ для робота.
 «Робот» (продолжение) В этой задаче мы впервые сталкиваемся с функцией трех переменных: F(X, Y, Z) - показывает количество маршрутов длины Z, приводящих в клетку (X, Y). К сожалению, такая структура данных как Array [-16. . 16, 0. . 16] of Long. Int; в память не помещается. Забудем пока об этой трудности и напишем рекурсивную часть. Для ответа на поставленный в задаче вопрос можно посчитать число маршрутов длины Z - 1 в четыре клетки, смежных с заданной, а результаты сложить, не забывая случаи клеток на границе. Граничными условиями будут F(X, Y, 0) = 0, если хотя бы одна из координат X или Y отлична от нуля, и F(0, 0, 0) = 1. Действительно, если робота не двигать, то он может оказаться только в начале координат. Теперь вспомним о проблеме хранения данных. Выхода существует два. Первый, чисто программистский, заключается в разбиении большой структуры на несколько меньших и размещении их в динамической памяти. Сделать это можно, например, так Type T 1 = array[-16. . 16, -16. . 16] of Long. Int; T 2 = array [0. . 16] of ^T 1; Var D : T 2;
«Робот» (продолжение) В этой задаче мы впервые сталкиваемся с функцией трех переменных: F(X, Y, Z) - показывает количество маршрутов длины Z, приводящих в клетку (X, Y). К сожалению, такая структура данных как Array [-16. . 16, 0. . 16] of Long. Int; в память не помещается. Забудем пока об этой трудности и напишем рекурсивную часть. Для ответа на поставленный в задаче вопрос можно посчитать число маршрутов длины Z - 1 в четыре клетки, смежных с заданной, а результаты сложить, не забывая случаи клеток на границе. Граничными условиями будут F(X, Y, 0) = 0, если хотя бы одна из координат X или Y отлична от нуля, и F(0, 0, 0) = 1. Действительно, если робота не двигать, то он может оказаться только в начале координат. Теперь вспомним о проблеме хранения данных. Выхода существует два. Первый, чисто программистский, заключается в разбиении большой структуры на несколько меньших и размещении их в динамической памяти. Сделать это можно, например, так Type T 1 = array[-16. . 16, -16. . 16] of Long. Int; T 2 = array [0. . 16] of ^T 1; Var D : T 2;
 «Робот» (продолжение) Это, конечно, решение, но оно далеко не оптимальное (с точки зрения расходования памяти). Действительно, для вычислений в некий момент времени необходимы данные только за предыдущий, что же происходило ранее, нас не интересует - с этим мы уже справились. Значит, достаточно хранить только 2 квадратные матрицы размером 31, - одна несет данные в предыдущий момент времени, а вторая вычисляется для текущего с использованием первой матрицы. После окончания расчета данные первой уже не нужны, ей присваиваем значение второй матрицы, увеличиваем счетчик времени и т. д. Ясно, что такую идею можно реализовать только итеративно.
«Робот» (продолжение) Это, конечно, решение, но оно далеко не оптимальное (с точки зрения расходования памяти). Действительно, для вычислений в некий момент времени необходимы данные только за предыдущий, что же происходило ранее, нас не интересует - с этим мы уже справились. Значит, достаточно хранить только 2 квадратные матрицы размером 31, - одна несет данные в предыдущий момент времени, а вторая вычисляется для текущего с использованием первой матрицы. После окончания расчета данные первой уже не нужны, ей присваиваем значение второй матрицы, увеличиваем счетчик времени и т. д. Ясно, что такую идею можно реализовать только итеративно.
 «Робот» (продолжение) Program robot; Var Way 1, Way 2: array [-16. . 16, 16. . 16] of longint; X, Y, K, i, j, z: shortint; s: longint; begin readln(K, X, Y); for i: =-16 to 16 do for j: =-16 to 16 do Way 1[i, j]: =0; Way 1[0, 0]: =1; for z: =1 to k do begin Way 2: =Way 1; for i: =-16 to 16 do for j: =-16 to 16 do begin s: =0; if i<>-16 then s: =s+Way 2[i-1, j]; if i<>16 then s: =s+Way 2[i+1, j]; if j<>-16 then s: =s+Way 2[i, j-1]; if j<>16 then s: =s+Way 2[i, j+1]; Way 1[i, j]: =s; end; writeln(way 1[x, y]); end.
«Робот» (продолжение) Program robot; Var Way 1, Way 2: array [-16. . 16, 16. . 16] of longint; X, Y, K, i, j, z: shortint; s: longint; begin readln(K, X, Y); for i: =-16 to 16 do for j: =-16 to 16 do Way 1[i, j]: =0; Way 1[0, 0]: =1; for z: =1 to k do begin Way 2: =Way 1; for i: =-16 to 16 do for j: =-16 to 16 do begin s: =0; if i<>-16 then s: =s+Way 2[i-1, j]; if i<>16 then s: =s+Way 2[i+1, j]; if j<>-16 then s: =s+Way 2[i, j-1]; if j<>16 then s: =s+Way 2[i, j+1]; Way 1[i, j]: =s; end; writeln(way 1[x, y]); end.
![«Робот» (продолжение) Program robot; Type T 1=array [-16. . 16, -16. . 16] «Робот» (продолжение) Program robot; Type T 1=array [-16. . 16, -16. . 16]](https://present5.com/presentation/3/102677620_388896621.pdf-img/102677620_388896621.pdf-28.jpg) «Робот» (продолжение) Program robot; Type T 1=array [-16. . 16, -16. . 16] of longint; T 2=array [0. . 16] of ^T 1; Var X, Y, K, i, j, z: shortint; s: longint; D: T 2; Function F(X, Y, Z: integer): longint; var s: longint; begin if D[Z]^[X, Y]=-1 then begin s: =0; if X<>-16 then s: =s+F(X-1, Y, Z-1); if X<>16 then s: =s+F(X+1, Y, Z-1); if Y<>-16 then s: =s+F(X, Y-1, Z-1); if Y<>16 then s: =s+F(X, Y+1, Z-1); D[Z]^[X, Y]: =s; end; F: =D[Z]^[X, Y]; end; Begin for i: =0 to 16 do New(D[i]); readln(K, X, Y); for i: =-16 to 16 do for j: =-16 to 16 do D[0]^[i, j]: =0; D[0]^[0, 0]: =1; for i: =-16 to 16 do for j: =-16 to 16 do for z: =1 to 16 do D[z]^[i, j]: =-1; writeln(F(x, y, k)); for i: =0 to 16 do Dispose(D[i]); end.
«Робот» (продолжение) Program robot; Type T 1=array [-16. . 16, -16. . 16] of longint; T 2=array [0. . 16] of ^T 1; Var X, Y, K, i, j, z: shortint; s: longint; D: T 2; Function F(X, Y, Z: integer): longint; var s: longint; begin if D[Z]^[X, Y]=-1 then begin s: =0; if X<>-16 then s: =s+F(X-1, Y, Z-1); if X<>16 then s: =s+F(X+1, Y, Z-1); if Y<>-16 then s: =s+F(X, Y-1, Z-1); if Y<>16 then s: =s+F(X, Y+1, Z-1); D[Z]^[X, Y]: =s; end; F: =D[Z]^[X, Y]; end; Begin for i: =0 to 16 do New(D[i]); readln(K, X, Y); for i: =-16 to 16 do for j: =-16 to 16 do D[0]^[i, j]: =0; D[0]^[0, 0]: =1; for i: =-16 to 16 do for j: =-16 to 16 do for z: =1 to 16 do D[z]^[i, j]: =-1; writeln(F(x, y, k)); for i: =0 to 16 do Dispose(D[i]); end.
 Задача о наибольшей общей подпоследовательности (НОП) В различных биологических задачах часто необходимо сравнивать ДНК двух или нескольких организмов. Моделью молекулы ДНК можно считать строку, над алфавитом из четырех символов (А, Г, Ц, Т). Тогда поставить задачу можно следующим образом: даны две строки, требуется найти подпоследовательность наибольшей длины, входящую в оба слова. Теперь формализуем задачу в несколько более общем случае. Пусть у нас есть последовательность X = {x 1, x 2, …, xm}, тогда другая последовательность Z = {z 1, z 2, …, zk} будет подпоследовательностью X, если существует такая возрастающая последовательность индексов I = {i 1, i 2, …, im}, что для всех j = 1, 2, …, k, будет верно равенство xij = zj. Пример. Z = {B, C, D, B} — подпоследовательность X = {A, B, C, B, D, A, B} с набором индексов {2, 3, 5, 7}.
Задача о наибольшей общей подпоследовательности (НОП) В различных биологических задачах часто необходимо сравнивать ДНК двух или нескольких организмов. Моделью молекулы ДНК можно считать строку, над алфавитом из четырех символов (А, Г, Ц, Т). Тогда поставить задачу можно следующим образом: даны две строки, требуется найти подпоследовательность наибольшей длины, входящую в оба слова. Теперь формализуем задачу в несколько более общем случае. Пусть у нас есть последовательность X = {x 1, x 2, …, xm}, тогда другая последовательность Z = {z 1, z 2, …, zk} будет подпоследовательностью X, если существует такая возрастающая последовательность индексов I = {i 1, i 2, …, im}, что для всех j = 1, 2, …, k, будет верно равенство xij = zj. Пример. Z = {B, C, D, B} — подпоследовательность X = {A, B, C, B, D, A, B} с набором индексов {2, 3, 5, 7}.
 НОП (продолжение) Говорят, что Z — общая подпоследовательность X и Y, если она является подпоследовательностью для X и Y. Тогда определим наибольшую общую подпоследовательность (НОП) двух данных последовательностей как общую подпоследовательность с максимальной длиной.
НОП (продолжение) Говорят, что Z — общая подпоследовательность X и Y, если она является подпоследовательностью для X и Y. Тогда определим наибольшую общую подпоследовательность (НОП) двух данных последовательностей как общую подпоследовательность с максимальной длиной.
 НОП (продолжение) Нахождения НОП двух заданных последовательностей X = {x 1, x 2, …, xn} и Y = {y 1, y 2, …, ym}: Если xn = ym, то мы должны искать НОП для Xn-1 и Ym -1 и, присоединив к этому результату xn = ym, мы получим НОП для X и Y. Если же xn ≠ ym, то мы должны решить две подзадачи: первая НОП Xn-1 и Y, вторая найти НОП X и Ym-1. Затем выбрать наибольший из двух результатов, это и будет НОП X и Y. Заметим, что каждая из двух подзадач потребует решения вновь появившихся подзадач, которые в свою очередь будут выявлять все новые подзадачи.
НОП (продолжение) Нахождения НОП двух заданных последовательностей X = {x 1, x 2, …, xn} и Y = {y 1, y 2, …, ym}: Если xn = ym, то мы должны искать НОП для Xn-1 и Ym -1 и, присоединив к этому результату xn = ym, мы получим НОП для X и Y. Если же xn ≠ ym, то мы должны решить две подзадачи: первая НОП Xn-1 и Y, вторая найти НОП X и Ym-1. Затем выбрать наибольший из двух результатов, это и будет НОП X и Y. Заметим, что каждая из двух подзадач потребует решения вновь появившихся подзадач, которые в свою очередь будут выявлять все новые подзадачи.
 НОП (продолжение) Остается только выбрать какой из двух алгоритмов прогонки здесь больше подходит, прямой или обратной. С вычислительной точки зрения наиболее рациональным будет алгоритм прямой прогонки, вычисляющий НОП снизу вверх. В случае вычисления очень удобно организовать в виде таблицы c[0…n, 0…m], где c[i][j] соответствует длине НОП префиксов Xi и Yj. Значение c[i][j] можем вычислять по следующим правилам: · 0, если i = 0 или j = 0; · c[I-1][j-1] + 1, если i, j > 0 и xi = yj; · max(c[i][j-1], c[I-1][j]), если i, j > 0 и xi ≠ yj.
НОП (продолжение) Остается только выбрать какой из двух алгоритмов прогонки здесь больше подходит, прямой или обратной. С вычислительной точки зрения наиболее рациональным будет алгоритм прямой прогонки, вычисляющий НОП снизу вверх. В случае вычисления очень удобно организовать в виде таблицы c[0…n, 0…m], где c[i][j] соответствует длине НОП префиксов Xi и Yj. Значение c[i][j] можем вычислять по следующим правилам: · 0, если i = 0 или j = 0; · c[I-1][j-1] + 1, если i, j > 0 и xi = yj; · max(c[i][j-1], c[I-1][j]), если i, j > 0 и xi ≠ yj.
 НОП (продолжение) Таким образом, мы можем найти длину НОП, а для того чтобы найти саму НОП, необходимо хранить некоторую дополнительную информацию. Удобно хранить информацию, о том, по какому условию осуществляется переход. На примере это можно проиллюстрировать с помощью стрелочек, тогда, возвращаясь назад по стрелочкам, мы найдем все символы, которые входят в НОП. На псевдокоде это будет выглядеть так LCS-LENGTH(X, Y) 1 m = length[X] 2 n = length[Y] 3 for i = 1 to n 4 do c[i, 0] = 0 5 for i = 1 to m 6 do c[0, j] = 0 7 for i = 1 to m do 8 do for j = 1 to n 9 do if xi = yj 10 then c[i, j] = c[i - 1, j - 1] + 1; 11 b[i, j] = «↖» 12 else if c[i - 1, j] ≥ c[i, j - 1] 13 then c[i, j] = c[i - 1, j] 14 b[i, j] = «↑» 15 else c[i, j] = c[i, j - 1] 16 b[i, j] = «←» 17 return b, c
НОП (продолжение) Таким образом, мы можем найти длину НОП, а для того чтобы найти саму НОП, необходимо хранить некоторую дополнительную информацию. Удобно хранить информацию, о том, по какому условию осуществляется переход. На примере это можно проиллюстрировать с помощью стрелочек, тогда, возвращаясь назад по стрелочкам, мы найдем все символы, которые входят в НОП. На псевдокоде это будет выглядеть так LCS-LENGTH(X, Y) 1 m = length[X] 2 n = length[Y] 3 for i = 1 to n 4 do c[i, 0] = 0 5 for i = 1 to m 6 do c[0, j] = 0 7 for i = 1 to m do 8 do for j = 1 to n 9 do if xi = yj 10 then c[i, j] = c[i - 1, j - 1] + 1; 11 b[i, j] = «↖» 12 else if c[i - 1, j] ≥ c[i, j - 1] 13 then c[i, j] = c[i - 1, j] 14 b[i, j] = «↑» 15 else c[i, j] = c[i, j - 1] 16 b[i, j] = «←» 17 return b, c
 НОП (продолжение) На следующем рисунке показана работа алгоритма для X = {A, B, C, B, D, A, B} и Y = {B, D, C, A, B, A}
НОП (продолжение) На следующем рисунке показана работа алгоритма для X = {A, B, C, B, D, A, B} и Y = {B, D, C, A, B, A}
 НОП (продолжение) Теперь покажем, как непосредственно найти саму НОП. PRINT_LCS(b, X, i, j) 1 if i = 0 or j = 0 2 then return 3 if b[i, j] = «↖» 4 then PRINT_LCS(b, X, i - 1, j - 1) 5 print xi 6 else if b[im, j] = «↑» 7 then PRINT_LCS(b, X, i - 1, j) 8 else PRINT_LCS (b, X, i, j - 1) решение
НОП (продолжение) Теперь покажем, как непосредственно найти саму НОП. PRINT_LCS(b, X, i, j) 1 if i = 0 or j = 0 2 then return 3 if b[i, j] = «↖» 4 then PRINT_LCS(b, X, i - 1, j - 1) 5 print xi 6 else if b[im, j] = «↑» 7 then PRINT_LCS(b, X, i - 1, j) 8 else PRINT_LCS (b, X, i, j - 1) решение
 Задача о загрузке (об оптимальном распределении ресурсов) Задача о загрузке — это задача о рациональной загрузке судна (самолета, автомашины, и т. п. ), которое имеет ограничения по объему или грузоподъемности. Каждый помещенный на судно груз приносит определенную прибыль. Задача состоит в том, чтобы определении загрузки, такими грузами которые приносят наибольшую прибыль. Задача о загрузке является типичным представителем задачи распределения ресурсов, в которой ограниченный ресурс распределяется между конечным числом видов (экономической) деятельности. В таких моделях определения состояния на каждом этапе будет аналогично приведенному для задачи о загрузке : состоянием на этапе i является суммарное количество ресурса, распределяемого на этапах i, i+1, …, n.
Задача о загрузке (об оптимальном распределении ресурсов) Задача о загрузке — это задача о рациональной загрузке судна (самолета, автомашины, и т. п. ), которое имеет ограничения по объему или грузоподъемности. Каждый помещенный на судно груз приносит определенную прибыль. Задача состоит в том, чтобы определении загрузки, такими грузами которые приносят наибольшую прибыль. Задача о загрузке является типичным представителем задачи распределения ресурсов, в которой ограниченный ресурс распределяется между конечным числом видов (экономической) деятельности. В таких моделях определения состояния на каждом этапе будет аналогично приведенному для задачи о загрузке : состоянием на этапе i является суммарное количество ресурса, распределяемого на этапах i, i+1, …, n.
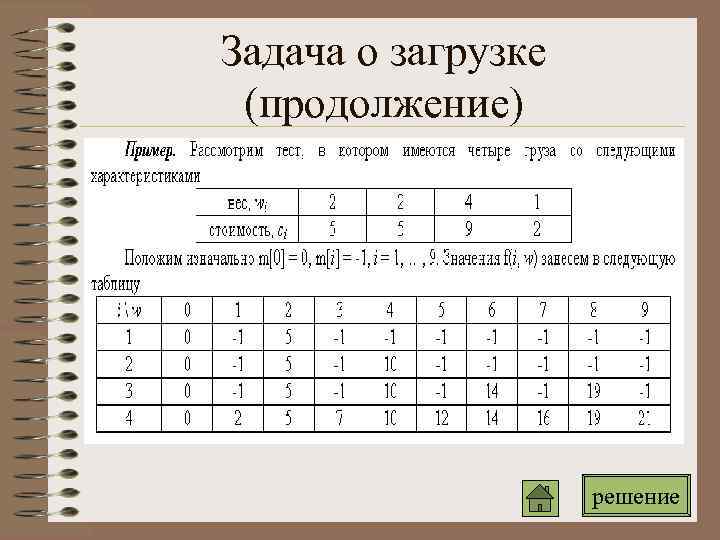
 Задача о загрузке (продолжение) Имеется судно грузоподъемностью w и n предметов. Известно, что i - ый предмет имеет вес wi и ценность ci. Необходимо загрузить судно предметами так, чтобы получить максимальную прибыль. Вход. Первая строка содержит количество предметов n и грузоподъемность судна w. Следующие n строк содержат характеристики грузов: в i - ой строке находится вес wi и ценность ci i - го груза. Выход. Максимальная суммарная ценность грузов, которыми можно загрузить судно. Пример входа Пример выхода 4 9 21 2 5 4 9 1 2
Задача о загрузке (продолжение) Имеется судно грузоподъемностью w и n предметов. Известно, что i - ый предмет имеет вес wi и ценность ci. Необходимо загрузить судно предметами так, чтобы получить максимальную прибыль. Вход. Первая строка содержит количество предметов n и грузоподъемность судна w. Следующие n строк содержат характеристики грузов: в i - ой строке находится вес wi и ценность ci i - го груза. Выход. Максимальная суммарная ценность грузов, которыми можно загрузить судно. Пример входа Пример выхода 4 9 21 2 5 4 9 1 2
 Задача о загрузке (продолжение) Обозначим через f(i, w) максимальную стоимость, которую можно получить имея лишь первые i грузов и грузоподъемность w. Если i - ый груз не использовался при подсчете f(i, w), то f(i, w) = f(i – 1, w). Иначе значение f(i, w) равно f(i – 1, w - wi) + ci. Отсюда получаем рекуррентное соотношение: f(i, w) = max( f(i – 1, w), f(i – 1, w - wi) + ci), i > 1 f(1, wi) = ci
Задача о загрузке (продолжение) Обозначим через f(i, w) максимальную стоимость, которую можно получить имея лишь первые i грузов и грузоподъемность w. Если i - ый груз не использовался при подсчете f(i, w), то f(i, w) = f(i – 1, w). Иначе значение f(i, w) равно f(i – 1, w - wi) + ci. Отсюда получаем рекуррентное соотношение: f(i, w) = max( f(i – 1, w), f(i – 1, w - wi) + ci), i > 1 f(1, wi) = ci
 Задача о загрузке (продолжение) решение
Задача о загрузке (продолжение) решение
 Задача о рюкзаке состоит в том, чтобы определить наиболее ценную выборку из n предметов, подлежащих упаковке в рюкзак, имеющий ограничение по весу, равное W килограмм. При этом i-ый предмет характеризуется стоимостью сi и весом wi. Итак, необходимо выбрать из этих предметов такой набор, чтобы суммарная масса не превосходила заданной величины W, а суммарная стоимость была максимальна.
Задача о рюкзаке состоит в том, чтобы определить наиболее ценную выборку из n предметов, подлежащих упаковке в рюкзак, имеющий ограничение по весу, равное W килограмм. При этом i-ый предмет характеризуется стоимостью сi и весом wi. Итак, необходимо выбрать из этих предметов такой набор, чтобы суммарная масса не превосходила заданной величины W, а суммарная стоимость была максимальна.
 Задача о рюкзаке (продолжение) Обозначим через T(n, W) функцию, значение которой соответствует решению нашей задачи. Аргументами функции является количество предметов n, по которому можно определить стоимость и массу каждого предмета, и ограничение по весу W. Определим подзазачи, решением которых будут функции T(i, j), а именно, определим максимальную стоимость предметов, которые можно уложить в рюкзак с ограничением по весу j килограмм, если можно использовать только первые i предметов из заданных. Здесь i и j по-прежнему целые числа и 0 ≤ i ≤ n, 0 ≤ j ≤ n. Определим начальные значения функции T следующим образом. T(0, 0) = 0, T(0, j) = 0 при j ≥ 1 (нет предметов, максимальная стоимость равна 0), T(i, 0) = 0 при i ≥ 1 (можно брать любые из первых i предметов, но ограничение по весу равно 0).
Задача о рюкзаке (продолжение) Обозначим через T(n, W) функцию, значение которой соответствует решению нашей задачи. Аргументами функции является количество предметов n, по которому можно определить стоимость и массу каждого предмета, и ограничение по весу W. Определим подзазачи, решением которых будут функции T(i, j), а именно, определим максимальную стоимость предметов, которые можно уложить в рюкзак с ограничением по весу j килограмм, если можно использовать только первые i предметов из заданных. Здесь i и j по-прежнему целые числа и 0 ≤ i ≤ n, 0 ≤ j ≤ n. Определим начальные значения функции T следующим образом. T(0, 0) = 0, T(0, j) = 0 при j ≥ 1 (нет предметов, максимальная стоимость равна 0), T(i, 0) = 0 при i ≥ 1 (можно брать любые из первых i предметов, но ограничение по весу равно 0).
 Задача о рюкзаке (продолжение) Для решения подзадачи, соответствующей функции T(i, j), рассмотрим два случая. Если i-ый предмет не упаковывается в рюкзак, то решение задачи с i предметами сводится к решению задачи с i – 1 предметом, т. е. T(i, j) = T(i - 1, j). Если же i-ый предмет упаковывается в рюкзак, то масса оставшихся предметов уменьшается на величину wi, а от добавления i-го предмета стоимость выборки увеличивается на ci. Следовательно, T(i, j) = T(i -1, j wi) + ci. При этом нужно учитывать, что эта ситуация возможна только тогда, когда масса i-го предмета не больше значения j.
Задача о рюкзаке (продолжение) Для решения подзадачи, соответствующей функции T(i, j), рассмотрим два случая. Если i-ый предмет не упаковывается в рюкзак, то решение задачи с i предметами сводится к решению задачи с i – 1 предметом, т. е. T(i, j) = T(i - 1, j). Если же i-ый предмет упаковывается в рюкзак, то масса оставшихся предметов уменьшается на величину wi, а от добавления i-го предмета стоимость выборки увеличивается на ci. Следовательно, T(i, j) = T(i -1, j wi) + ci. При этом нужно учитывать, что эта ситуация возможна только тогда, когда масса i-го предмета не больше значения j.
 Задача о рюкзаке (продолжение) Теперь для оптимального решения из двух возможных вариантов упаковки рюкзака нужно выбрать наилучший. Рекурентное соотношение при i ≥ 1 и j ≥ 1 имеет следующий вид: T(i, j)= T(i -1, j) при j < wi T(i, j)= max (T(i -1, j), T(i -1, j - wi) + ci) при j ≥ wi.
Задача о рюкзаке (продолжение) Теперь для оптимального решения из двух возможных вариантов упаковки рюкзака нужно выбрать наилучший. Рекурентное соотношение при i ≥ 1 и j ≥ 1 имеет следующий вид: T(i, j)= T(i -1, j) при j < wi T(i, j)= max (T(i -1, j), T(i -1, j - wi) + ci) при j ≥ wi.
 Задача о рюкзаке (продолжение) Пример. Пусть заданы следующие значения стоимости и массы для 5 предметов и ограничение веса 16 кг. : c 1 = 5, w 1 = 4; c 2 = 7, w 2 = 5; c 3 = 4, w 3 = 3; c 4 = 9, w 4 = 7; c 5 = 8, w 5 = 6.
Задача о рюкзаке (продолжение) Пример. Пусть заданы следующие значения стоимости и массы для 5 предметов и ограничение веса 16 кг. : c 1 = 5, w 1 = 4; c 2 = 7, w 2 = 5; c 3 = 4, w 3 = 3; c 4 = 9, w 4 = 7; c 5 = 8, w 5 = 6.
 Задача о рюкзаке (продолжение) Таблица значений функции T выглядит следующим образом.
Задача о рюкзаке (продолжение) Таблица значений функции T выглядит следующим образом.
 Задача о рюкзаке (продолжение) Как определить тот набор предметов, которые подлежат упаковке в рюкзак? Сравним значение T[n, W] со значением T[n-1, W]. Если T[n-1, W] ≠ T[n-1, W], то предмет c номером n обязательно упаковывается в рюкзак, после чего переходим к сравнению элементов T[n-1, W - wn] и T[n-2, W- wn] и т. д. Если-же T[n-1, W] = T[n-1, W], то n-ый предмет можно не упаковывать в рюкзак, так максимальная стоимость набрана без него. В этом случае следует перейти к рассмотрению элементов T[n-1, W] и T[n-2, W].
Задача о рюкзаке (продолжение) Как определить тот набор предметов, которые подлежат упаковке в рюкзак? Сравним значение T[n, W] со значением T[n-1, W]. Если T[n-1, W] ≠ T[n-1, W], то предмет c номером n обязательно упаковывается в рюкзак, после чего переходим к сравнению элементов T[n-1, W - wn] и T[n-2, W- wn] и т. д. Если-же T[n-1, W] = T[n-1, W], то n-ый предмет можно не упаковывать в рюкзак, так максимальная стоимость набрана без него. В этом случае следует перейти к рассмотрению элементов T[n-1, W] и T[n-2, W].
![Задача о рюкзаке (продолжение) В нашем примере T[5, 16] = T[4, 16], поэтому 5 Задача о рюкзаке (продолжение) В нашем примере T[5, 16] = T[4, 16], поэтому 5](https://present5.com/presentation/3/102677620_388896621.pdf-img/102677620_388896621.pdf-47.jpg) Задача о рюкзаке (продолжение) В нашем примере T[5, 16] = T[4, 16], поэтому 5 -ый предмет в рюкзак не упаковывается. Переходим к сравнению элементов таблицы T[4, 16] и T[3, 16]. Их значения не равны, следовательно, четвертый предмет должен быть включен в искомый набор, а ограничение на вес становится равным 16 - w 5 = 16 – 7 =9. Далее сравним элементы T[3, 9] и T[2, 9], они равны, следовательно третий предмет в рюкзак не упаковывается. Переходим к сравнению T[2, 9] и T[1, 9], они не совпадают, следовательно, второй предмет должен быть взят в рюкзак, а ограничение на вес становится равным 9 - w 2 = 9 – 5 =4. И последнее: сравниваем элементы T[1, 4] и T[0, 4], они не равны, поэтому второй предмет включатся в искомый набор, при этом, ограничение по весу становится равным 0. Итак, для нашего примера в рюкзак упакуются предметы с номерами 1, 2, 4.
Задача о рюкзаке (продолжение) В нашем примере T[5, 16] = T[4, 16], поэтому 5 -ый предмет в рюкзак не упаковывается. Переходим к сравнению элементов таблицы T[4, 16] и T[3, 16]. Их значения не равны, следовательно, четвертый предмет должен быть включен в искомый набор, а ограничение на вес становится равным 16 - w 5 = 16 – 7 =9. Далее сравним элементы T[3, 9] и T[2, 9], они равны, следовательно третий предмет в рюкзак не упаковывается. Переходим к сравнению T[2, 9] и T[1, 9], они не совпадают, следовательно, второй предмет должен быть взят в рюкзак, а ограничение на вес становится равным 9 - w 2 = 9 – 5 =4. И последнее: сравниваем элементы T[1, 4] и T[0, 4], они не равны, поэтому второй предмет включатся в искомый набор, при этом, ограничение по весу становится равным 0. Итак, для нашего примера в рюкзак упакуются предметы с номерами 1, 2, 4.
 Задача о рюкзаке (продолжение) Ниже описана процедура, которая печатает номера предметов, подлежащие упаковке в рюкзак: procedure print_item(i, j: integer); begin if t[i, j]<>0 then if t[i-1, j]=t[i, j] then print_item(i-1, j) else begin print_item(i-1, j-w[i]); write(i, ' '); end; В программе нужно вызвать процедуру м параметрами (n, wes) решение
Задача о рюкзаке (продолжение) Ниже описана процедура, которая печатает номера предметов, подлежащие упаковке в рюкзак: procedure print_item(i, j: integer); begin if t[i, j]<>0 then if t[i-1, j]=t[i, j] then print_item(i-1, j) else begin print_item(i-1, j-w[i]); write(i, ' '); end; В программе нужно вызвать процедуру м параметрами (n, wes) решение
 Задачи для самостоятельного решения 1. Монеты. Имеются монеты достоинством v 1, v 2, …, vn копеек. Необходимо найти наименьшее количество монет, которыми можно выдать сумму S. Рассмотрим подзадачу, в которой требуется найти наименьшее количество монет, которыми можно выдать сумму i , i £ S. Обозначим решение этой подзадачи через f(i). Если известны все значения f(j), 1 ≤ j ≤ i, то легко найти f(i + 1): f(i + 1) = min f(i + 1 – vj) + 1, i + 1 ≥ vj 1 ≤ j ≤ n По умолчанию положим f(0) = 0, так как сумму в 0 копеек можно выдать 0 монетами. Значения решений для подзадач f(i) храним в некотором числовом массиве m. Пример. Пусть имеются монеты достоинством 1, 2 и 5 копеек. Значение искомой суммы равно S = 9. Значение элементов массива m имеет вид: Сумму в 9 копеек можно выдать так: 9 = 5 + 2. решение
Задачи для самостоятельного решения 1. Монеты. Имеются монеты достоинством v 1, v 2, …, vn копеек. Необходимо найти наименьшее количество монет, которыми можно выдать сумму S. Рассмотрим подзадачу, в которой требуется найти наименьшее количество монет, которыми можно выдать сумму i , i £ S. Обозначим решение этой подзадачи через f(i). Если известны все значения f(j), 1 ≤ j ≤ i, то легко найти f(i + 1): f(i + 1) = min f(i + 1 – vj) + 1, i + 1 ≥ vj 1 ≤ j ≤ n По умолчанию положим f(0) = 0, так как сумму в 0 копеек можно выдать 0 монетами. Значения решений для подзадач f(i) храним в некотором числовом массиве m. Пример. Пусть имеются монеты достоинством 1, 2 и 5 копеек. Значение искомой суммы равно S = 9. Значение элементов массива m имеет вид: Сумму в 9 копеек можно выдать так: 9 = 5 + 2. решение
 Задачи для самостоятельного решения • Документ1 «Динамическое программирование (Вальядолид, Топкодер)» • Документ2 «Е. В. Брызгалов Динамическое программирование»
Задачи для самостоятельного решения • Документ1 «Динамическое программирование (Вальядолид, Топкодер)» • Документ2 «Е. В. Брызгалов Динамическое программирование»
 Источники • Кормен Т. , Лейзерсон Ч. , Ривест Р. Алгоритмы: построение и анализ. — М. : МЦНМО, • 1999. • Ахо А. , Хопкрофт Д. , Ульман Д. Структуры данных и алгоритмы. — М. : Издательский • дом «Вильямс» , 2001. • Таха Х. Введение в исследование операций. — М. : Издательский дом «Вильямс» , 2001. • Беров В. И. , Лапунов А. В. , Матюхин В. А. , Пономарев А. Е. Особенности национальных • задач по информатике. — Киров: Триада-С, 2000. • http: //rain. ifmo. ru/cat/view. php/theory • [Вальядолид] acm. uva. es/problemset • [Топкодер] www. topcoder. com
Источники • Кормен Т. , Лейзерсон Ч. , Ривест Р. Алгоритмы: построение и анализ. — М. : МЦНМО, • 1999. • Ахо А. , Хопкрофт Д. , Ульман Д. Структуры данных и алгоритмы. — М. : Издательский • дом «Вильямс» , 2001. • Таха Х. Введение в исследование операций. — М. : Издательский дом «Вильямс» , 2001. • Беров В. И. , Лапунов А. В. , Матюхин В. А. , Пономарев А. Е. Особенности национальных • задач по информатике. — Киров: Триада-С, 2000. • http: //rain. ifmo. ru/cat/view. php/theory • [Вальядолид] acm. uva. es/problemset • [Топкодер] www. topcoder. com


