Динамические структуры данных Динамические структуры характеризуются отсутствием физической

Динамические структуры данных Динамические структуры характеризуются: отсутствием физической смежности элементов структуры в памяти; непостоянством и непредсказуемостью размера (числа элементов) структуры в процессе ее обработки. 1

Указатели • Поскольку элементы динамической структуры располагаются по непредсказуемым адресам памяти, адрес элемента такой структуры не может быть вычислен из адреса начального или предыдущего элемента. • Для установления связи между элементами динамической структуры используются указатели, через которые устанавливаются явные связи между элементами. Такое представление данных в памяти называется связным 2

Элемент динамической структуры • Элемент динамической структуры состоит из двух полей: – информационного поля или поля данных, в котором содержатся те данные, ради которых и создается структура; в общем случае информационное поле может быть интегрированной структурой - вектором, массивом, другой динамической структурой и т. п. ; – поле связок, в котором содержатся один или несколько указателей, связывающий данный элемент с другими элементами структуры; 3

Достоинства динамических структур данных – возможность обеспечения значительной изменчивости структур; – размер структуры ограничивается только доступным объемом машинной памяти; – при изменении логической последовательности элементов структуры требуется не перемещение данных в памяти, а только коррекция указателей. 4

недостатки динамических структур данных – на поля связок расходуется дополнительная память; – доступ к элементам связной структуры может быть менее эффективным по времени. • Последний недостаток является наиболее серьезным и именно им ограничивается применимость связного представления данных. • Дескриптор связной структуры содержит один или несколько указателей, позволяющих войти в структуру, далее поиск требуемого элемента выполняется следованием по цепочке указателей от элемента к элементу. Поэтому связное представление практически никогда не применяется в задачах, где логическая структура данных имеет вид вектора или массива - с доступом по номеру элемента, но часто применяется в задачах, где логическая структура требует другой исходной информации доступа (списки, деревья и т. д. ). 5

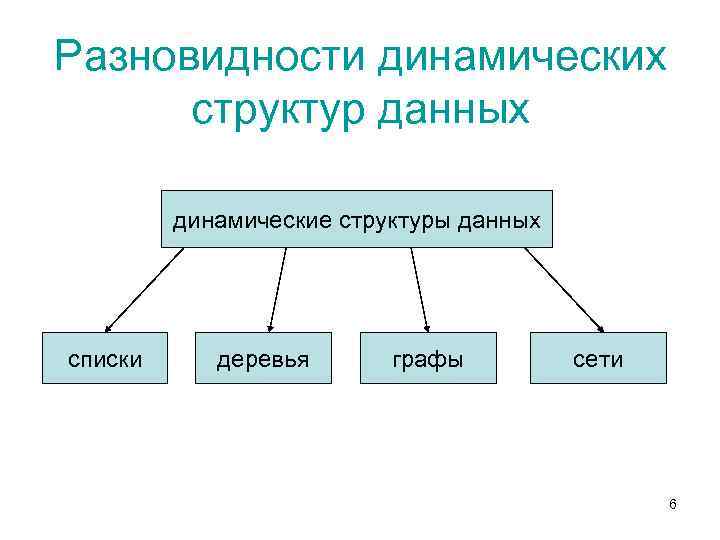Разновидности динамических структур данных динамические структуры данных списки деревья графы сети 6

Списки • Списком называется упорядоченное множество, состоящее из переменного числа элементов, к которым применимы операции включения, исключения. • Список, отражающий отношения соседства между элементами, называется линейным. • Длина списка равна числу элементов, содержащихся в списке, • Список нулевой длины называется пустым списком. • Линейные связные списки являются простейшими динамическими структурами данных. 7

односвязный список • На рисунке приведена структура односвязного списка. На нем поле INF - информационное поле, данные, NEXT - указатель на следующий элемент списка. • Каждый список должен иметь особый элемент, называемый указателем начала списка или головой списка, который обычно по формату отличен от остальных элементов. • В поле указателя последнего элемента списка находится специальный признак nil, свидетельствующий о конце списка. 8

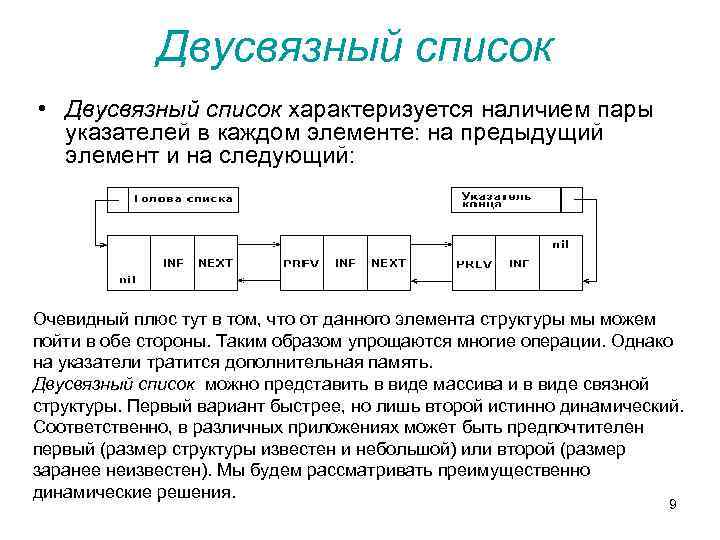Двусвязный список • Двусвязный список характеризуется наличием пары указателей в каждом элементе: на предыдущий элемент и на следующий: Очевидный плюс тут в том, что от данного элемента структуры мы можем пойти в обе стороны. Таким образом упрощаются многие операции. Однако на указатели тратится дополнительная память. Двусвязный список можно представить в виде массива и в виде связной структуры. Первый вариант быстрее, но лишь второй истинно динамический. Соответственно, в различных приложениях может быть предпочтителен первый (размер структуры известен и небольшой) или второй (размер заранее неизвестен). Мы будем рассматривать преимущественно динамические решения. 9

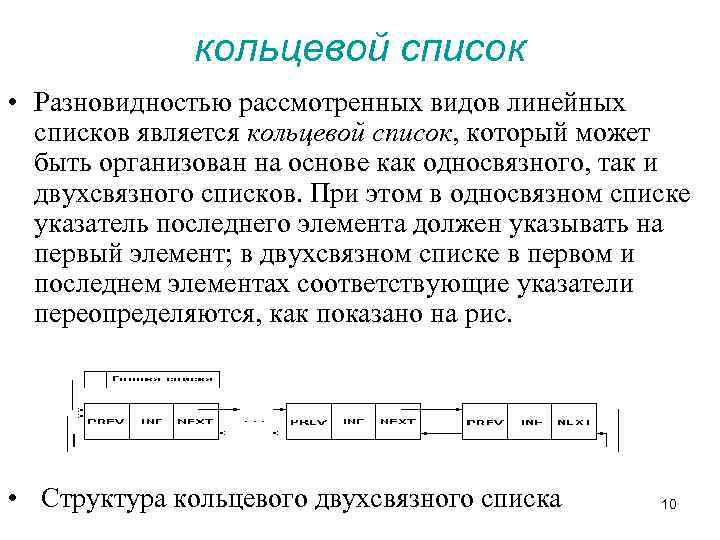кольцевой список • Разновидностью рассмотренных видов линейных списков является кольцевой список, который может быть организован на основе как односвязного, так и двухсвязного списков. При этом в односвязном списке указатель последнего элемента должен указывать на первый элемент; в двухсвязном списке в первом и последнем элементах соответствующие указатели переопределяются, как показано на рис. • Структура кольцевого двухсвязного списка 10

Особенности кольцевого списка • При работе с такими списками несколько упрощаются некоторые процедуры. Просмотр кольцевого списка можно начинать с любого места, а не только с головы списка, т. е. в качестве головы списка может служить любой из его элементов. • Однако, при просмотре такого списка следует принять некоторые меры предосторожности, чтобы не попасть в бесконечный цикл. 11

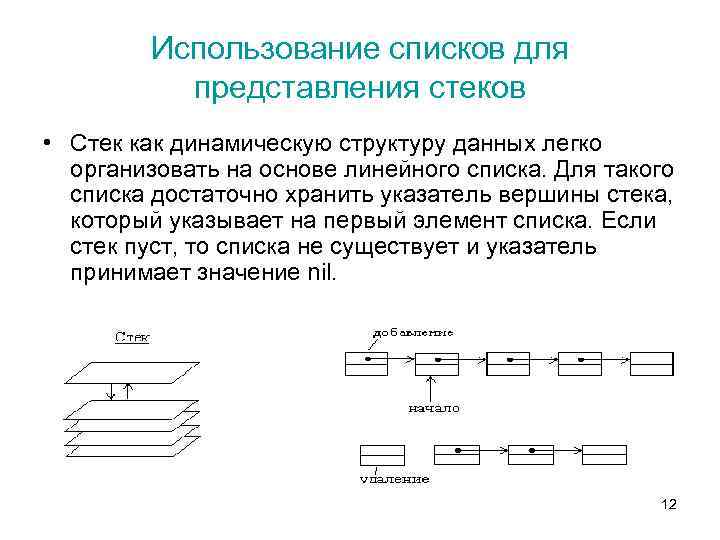Использование списков для представления стеков • Стек как динамическую структуру данных легко организовать на основе линейного списка. Для такого списка достаточно хранить указатель вершины стека, который указывает на первый элемент списка. Если стек пуст, то списка не существует и указатель принимает значение nil. 12

Использование списков для представления очередей • Представление очереди с помощью линейного связного списка позволяет достаточно просто обеспечивать любые желаемые дисциплины включения элементов в очередь и исключения их из очереди и достигать высокой гибкости в управлении памятью. По этой причине очереди с трудно предсказуемым числом элементов или очереди со специальными дисциплинами обработки, возникающие в ОС, при имитационном моделировании систем массового обслуживания, в задачах управления ресурсами и другие реализуются с помощью линейных связных списков. • Динамическая реализация очереди аналогична реализации стека. 13

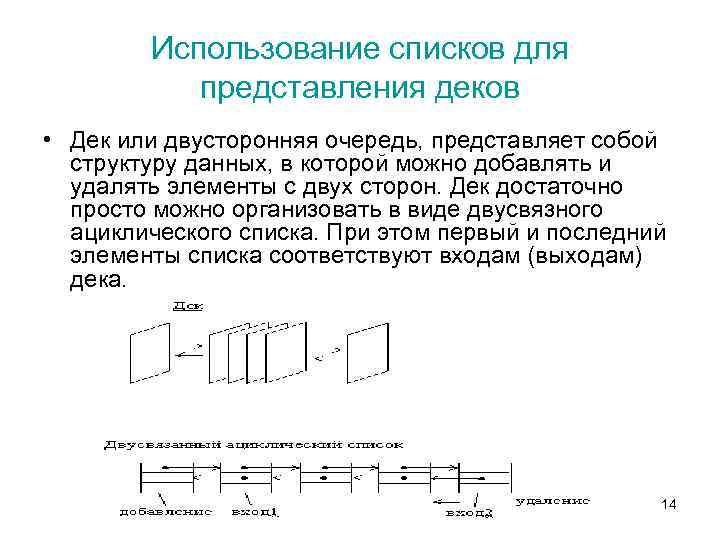Использование списков для представления деков • Дек или двусторонняя очередь, представляет собой структуру данных, в которой можно добавлять и удалять элементы с двух сторон. Дек достаточно просто можно организовать в виде двусвязного ациклического списка. При этом первый и последний элементы списка соответствуют входам (выходам) дека. 14

Нелинейные связные структуры • Односвязный список всегда линейный. • Двусвязный список может и не быть линейным, если второй указатель каждого элемента списка задает порядок произвольного вида, не являющийся обратным по отношению к порядку, устанавливаемому первым указателем элемента. • Если у элемента имеется более двух связей, то эта структура всегда нелинейная. 15

Свойства многосвязной структуры • Каждый элемент структуры содержит произвольное число направленных связок с другими (или ссылкой на другие элементы ) • С каждым элементом может связываться произвольное число других элементов ( т. е. каждый элемент может быть объектом ссылки произвольного числа других элементов ). • Каждая связка в структуре может иметь не только направление, но и вес. 16

Многосвязные списки (мультисписки) • В общем случае каждый элемент связного списка может содержать произвольное конечное число связок, одинаковое или разное в различных элементах. • В результате такого обобщения получается многосвязный список, каждый элемент которого входит одновременно во столько разных односвязных списков, сколько имеется связок в соответствующем элементе. • Иногда многосвязные списки называют прошитыми списками, плексами или мультисписками. 17

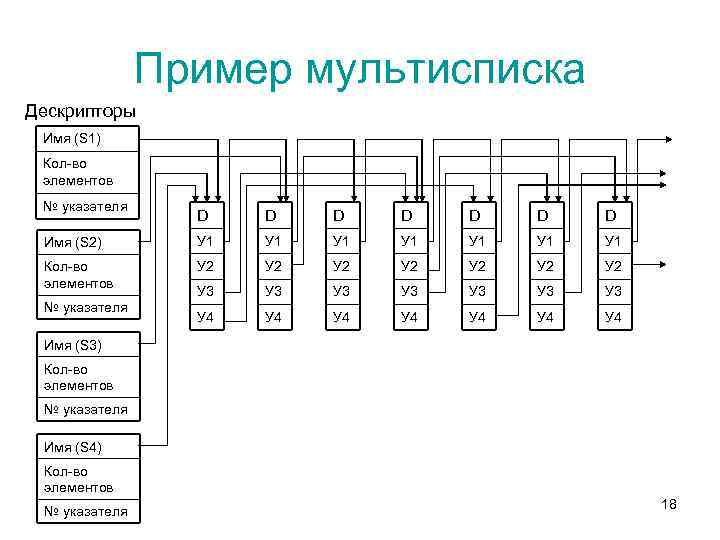Пример мультисписка Дескрипторы Имя (S 1) Кол-во элементов № указателя D D D D Имя (S 2) У 1 У 1 Кол-во элементов У 2 У 2 У 3 У 3 У 4 У 4 № указателя Имя (S 3) Кол-во элементов № указателя Имя (S 4) Кол-во элементов № указателя 18

Особенности мультисписков • К достоинствам мультисписков помимо экономии памяти (при множестве списков информационная часть существует в единственном экземпляре) следует отнести также целостность данных - в том смысле, что все подзадачи работают с одной и той же версией информационной части и изменения в данных, сделанные одной подзадачей немедленно становятся доступными для другой подзадачи. • Каждая подзадача работает со своим подмножеством как с линейным списком, используя для этого определенное поле связок. Исключение элемента из какого-либо одного списка еще не означает необходимости удаления элемента из памяти, так как элемент может оставаться в составе других списков. Обычно задача удаления упрощается тем, что один из частных списков является главным - в него обязательно входят все имеющиеся элементы. Тогда исключение элемента из любого неглавного списка состоит только в переопределении указателей, но не в освобождении памяти. Исключение же из главного списка требует не только освобождения памяти, но и переопределения указателей как в главном списке, так и во всех неглавных списках, в которые удаляемый элемент входил. 19

Другие виды многосвязных структур • Деревья - отношения одного ко многим • Графы - отношения многих ко многим • Сети - отношения многих ко многим имеют содержание. В зависимости от этого они разделяются: – Если отношения имеют вес, то сеть называется взвешенной; – Если отношения имеют смысл, то сеть называется семантической; – Если отношения отражают знания, то сеть называется фреймовой; – Если отношения носят вероятностный характер, то сеть называется Байесовской сетью; – И т. д. • Фреймы 20

Семантические сети • Семантическая сеть — это ориентированный граф, вершины которого — понятия, а дуги — отношения между ними. • Термин семантическая означает «смысловая» , а сама семантика — это наука, определяющая отношения между символами и объектами, которые они обозначают, то есть наука, определяющая смысл знаков. • В качестве понятий обычно выступают абстрактные или конкретные объекты, а отношения — это связи типа: «это» ( «АКО — A-Kind-Of>>, «is» ), «имеет частью» ( «has part» ), «принадлежит» , «любит» . 21

отношения в семантических сетях • класс — элемент класса (цветок — роза); • свойство — значение (цвет — желтый); • пример элемента класса (роза — чайная). 22

классификаций семантических сетей, по типам отношений. • По количеству типов отношений: 1. Однородные (с единственным типом отношений). 2. Неоднородные (с различными типами отношений). • По типам отношений: 1. Бинарные (в которых отношения связывают два объекта). 2. N-арные (в которых есть специальные отношения, связывающие более двух понятий). 23

частые отношения в семантических сетях • связи типа «часть — целое» ( «класс — подкласс» , «элемент -—множество» , и т. п. ); • функциональные связи (определяемые обычно глаголами «производит» , «влияет» . . . ); • количественные (больше, меньше, равно. . . ); • пространственные (далеко от, близко от, за, под, над. . . ); • временные (раньше, позже, в течение. . . ); • атрибутивные связи (иметь свойство, иметь значение); • логические связи (И, ИЛИ, НЕ); • лингвистические связи и др. 24

Поиск в семантической сети • Проблема поиска решения в базе знаний типа семантической сети сводится к задаче поиска фрагмента сети, соответствующего некоторой подсети, отражающей поставленный запрос к базе. 25

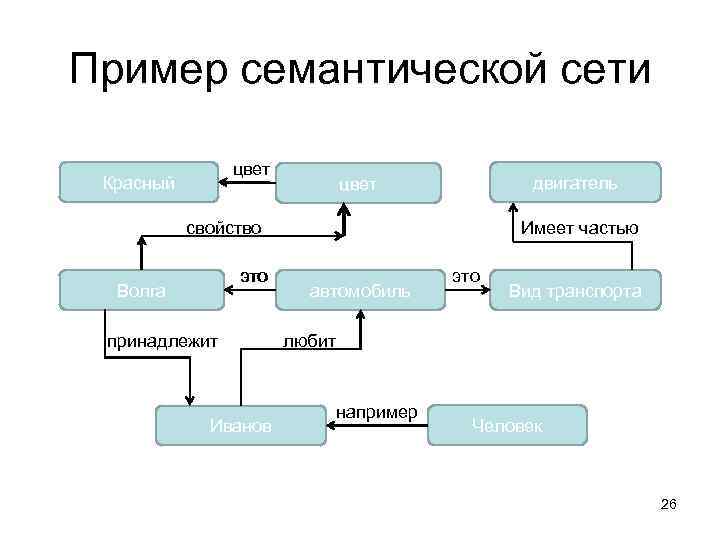Пример семантической сети цвет Красный двигатель цвет свойство это Волга принадлежит Иванов Имеет частью автомобиль это Вид транспорта любит например Человек 26

Инструменты для реализации семантических сетей • Для реализации семантических сетей существуют специальные сетевые языки, например NET [Цейтин, 1985], язык реализации систем SIMER+MIR [Осипов, 1997] и др. Широко известны экспертные системы, использующие семантические сети в качестве языка представления знаний — PROSPECTOR, CASNET, TORUS [Хейес-Рот и др. , 1987; Durkin, 1998]. 27

Фреймы • Термин фрейм (от английского frame, что означает «каркас» или «рамка» ) был предложен Маренном Минским для обозначения структуры знаний для восприятия пространственных сцен. Эта модель, как и семантическая сеть, имеет глубокое психологическое обоснование. • Фрейм — это абстрактный образ для представления некоего стереотипа восприятия. 28

понятие абстрактного образа • Например, произнесение вслух слова «комната» порождает у слушающих образ комнаты: «жилое помещение с четырьмя стенами, полом, потолком, окнами и дверью, площадью 6 -20 м 2» . Из этого описания ничего нельзя убрать (например, убрав окна, мы получим уже чулан, а не комнату), но в нем есть «дырки» или «слоты» — это незаполненные значения некоторых атрибутов — например, количество окон, цвет стен, высота потолка, покрытие пола и др. • В теории фреймов такой образ комнаты называется фреймом комнаты. • Фреймом также называется и формализованная модель для отображения образа 29

Разновидности фреймов • Различают фреймы-образцы, или прототипы, хранящиеся в базе знаний, и фреймы-экземпляры, которые создаются для отображения реальных фактических ситуаций на основе поступающих данных. 30

Разновидности фреймов • Модель фрейма является достаточно универсальной, поскольку позволяет отобразить все многообразие знаний о мире через: • фреймы-структуры, использующиеся для обозначения объектов и понятий • фреймы-роли; • фреймы-сценарии; • фреймы-ситуации. 31

структура фрейма • Традиционно структура фрейма может быть представлена как список свойств: (ИМЯ ФРЕЙМА: • (имя 1 -го слота: значение 1 -го слота), • (имя 2 -го слота: значение 2 -го слота), • ………… • (имя N-гo слота: значение N-гo слота)). 32

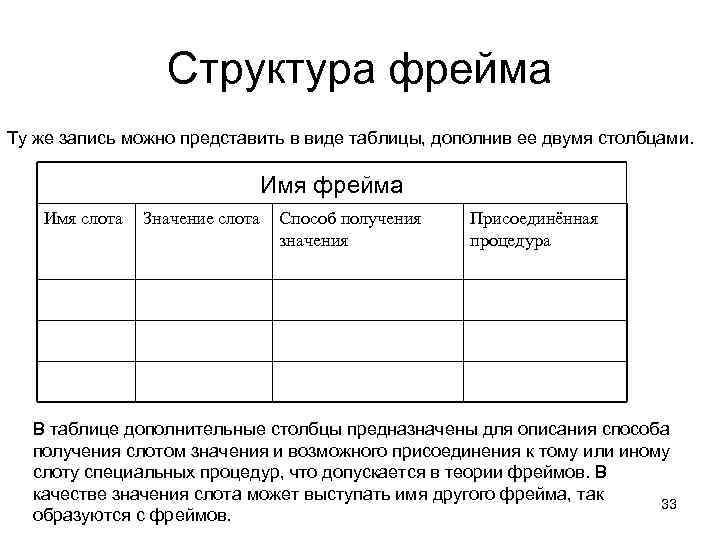Структура фрейма Ту же запись можно представить в виде таблицы, дополнив ее двумя столбцами. Имя фрейма Имя слота Значение слота Способ получения значения Присоединённая процедура В таблице дополнительные столбцы предназначены для описания способа получения слотом значения и возможного присоединения к тому или иному слоту специальных процедур, что допускается в теории фреймов. В качестве значения слота может выступать имя другого фрейма, так 33 образуются с фреймов.

способы получения слотом значений во фрейме-экземпляре • по умолчанию от фрейма-образца (Default-значение); • через наследование свойств от фрейма, указанного в слоте АКО; • по формуле, указанной в слоте; • через присоединенную процедуру; • явно из диалога с пользователем; • из базы данных. 34

• Важнейшим свойством теории фреймов является заимствование из теории семантических сетей — называемое наследование свойств. И во фреймах, и в семантических сетях наследование происходит по Ai связям (A-Kind-Of = это). Слот АКО указывает на фрейм более высокого уровня иерархии, откуда неявно наследуются, то есть переносятся, значения аналогичных слотов. 35

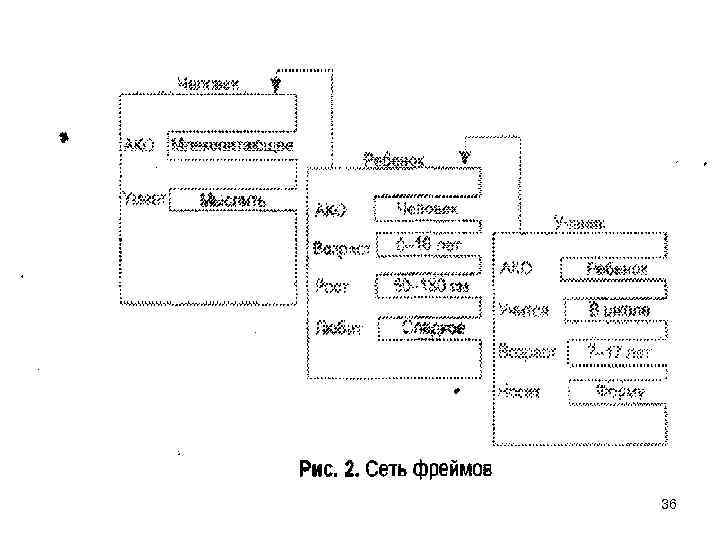36

языки представления знаний в сетях фреймов • Основным преимуществом фреймов как модели представления знаний является то, что она отражает концептуальную основу организации памяти человека [Шенк, Хантер, 1987], а также ее гибкость и наглядность. • Специальные языки представления знаний в сетях фреймов FRL (Frame Representation Language) [Байдун, Бунин, 1990], KRL (Knowledge Representation Language) [Уотермен, 1989], фреймовая «оболочка» Kappa [Стрельников, Борисов, 1997] и другие программные средства позволяют эффективно строить промышленные ЭС. Широко известны такие фрейм-ориентированные экспертные системы, как ANALYST, МОДИС, TRISTAN, ALTERID [Ковригин, Перфильев, 1988; Николов, 1988; Sisodia, Warkentin, 1992]. 37