ДИНАМИЧЕСКИЕ СТРУКТУРЫ ДАННЫХ Деревья Деревья Основные

ДИНАМИЧЕСКИЕ СТРУКТУРЫ ДАННЫХ

Деревья

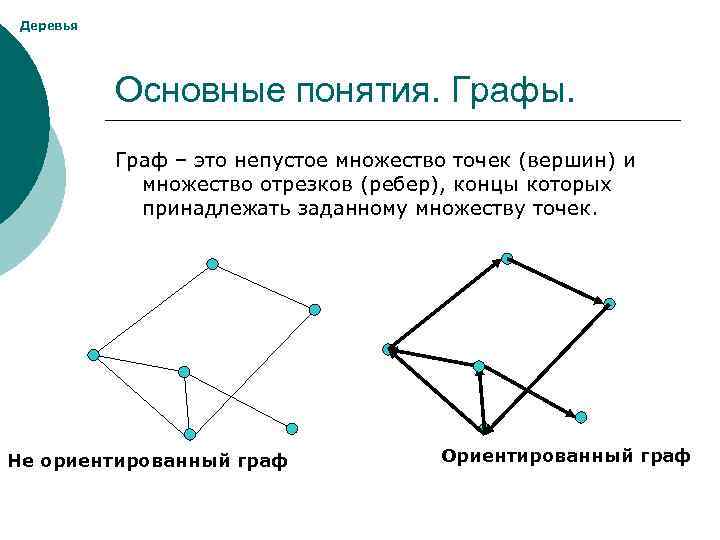Деревья Основные понятия. Графы. Граф – это непустое множество точек (вершин) и множество отрезков (ребер), концы которых принадлежать заданному множеству точек. Не ориентированный граф Ориентированный граф

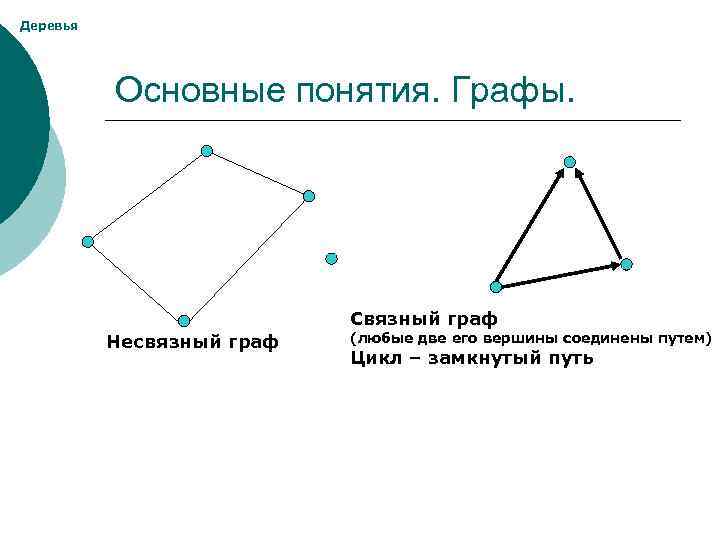Деревья Основные понятия. Графы. Связный граф Несвязный граф (любые две его вершины соединены путем) Цикл – замкнутый путь

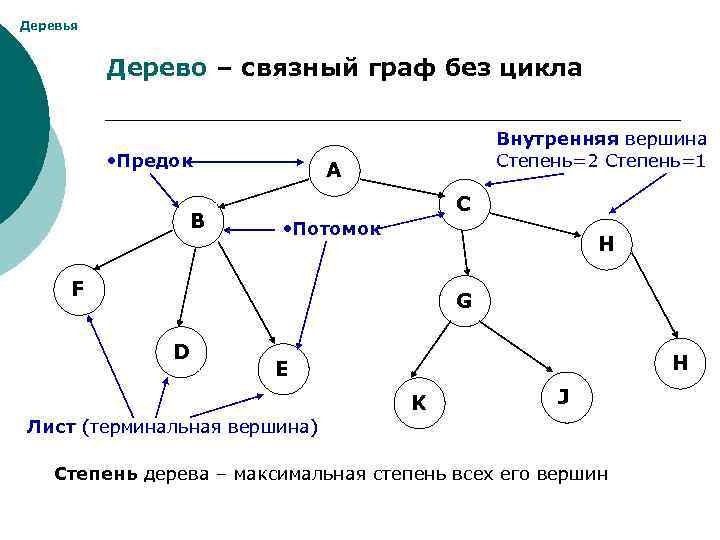Деревья Дерево – связный граф без цикла • Предок B Внутренняя вершина Степень=2 Степень=1 А C • Потомок H F G D H E K J Лист (терминальная вершина) Степень дерева – максимальная степень всех его вершин

Деревья Дерево – это сложная динамическая структура данных, применяющаяся для эффективного хранения и поиска информации

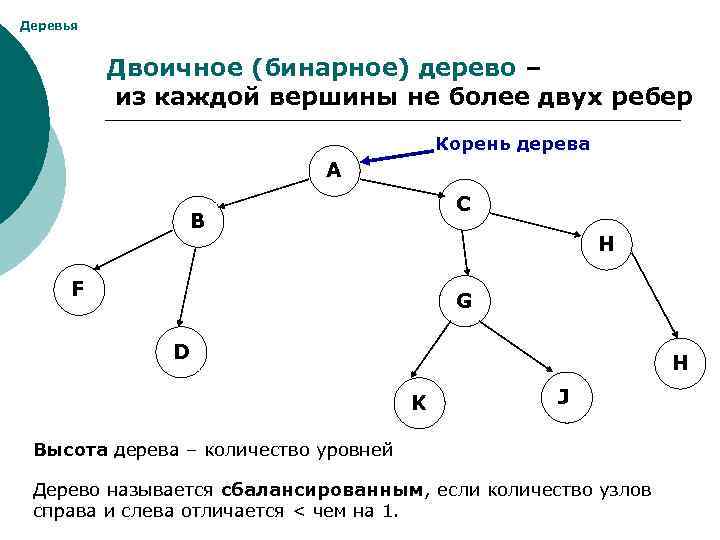Деревья Двоичное (бинарное) дерево – из каждой вершины не более двух ребер Корень дерева А C B H F G D H K J Высота дерева – количество уровней Дерево называется сбалансированным, если количество узлов справа и слева отличается < чем на 1.

Деревья Описание дерева Type Tree. Link=^Tree; Tree=Record Data: <тип данных> Left, Right: Tree. Link; End; Var kd: Tree. Link; {описание корня дерева}

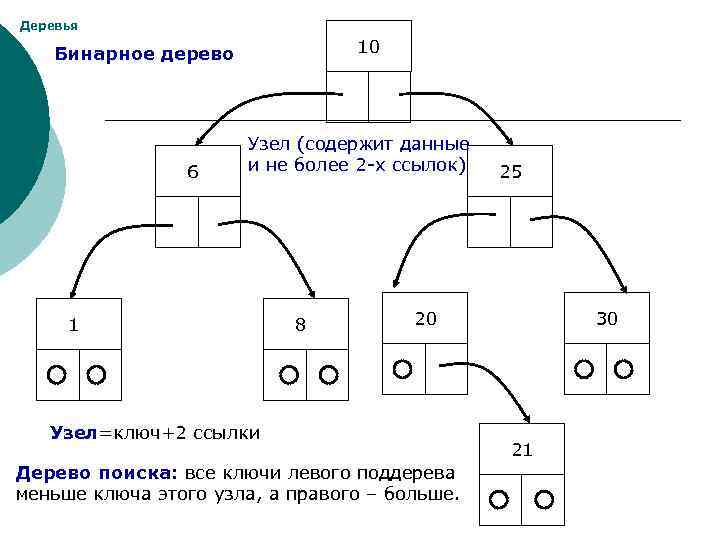Деревья 10 Бинарное дерево 6 Узел (содержит данные и не более 2 -х ссылок) 1 8 25 20 Узел=ключ+2 ссылки Дерево поиска: все ключи левого поддерева меньше ключа этого узла, а правого – больше. 30 21

Деревья Основные операции над деревьями Занесение элемента в дерево; ¡ Обход дерева; ¡ Удаление элемента из дерева. ¡

Деревья Создать и вывести на экран дерево поиска, элементы которого вводятся с клавиатуры и имеют целый тип. При вставке в дерево вершина вставляется: q как поддерево уже существующей вершины; q как единственная вершина дерева. Выводы: • и левая, и правая связи новой вершины должны быть равны Nil; • когда дерево пусто, значение передаваемой в виде параметра ссылки равно Nil. В этом случае нужно изменить ее так, чтобы она указывала на новую вершину, которая была вставлена как корневая. • при вставке второго элемента переданный из основной программы параметр t уже не будет равен Nil, и надо принимать решение о том, в какое поддерево необходимо вставить новую вершину.

Деревья Процедура вставки в дерево новой вершины Procedure Ins. Tree(n: Integer; Var t: treelink); Begin If t=NIL Then Begin new(t); With t^ Do Begin left: =Nil; t^. left: =Nil; right: =Nil; t^. data: =n End; End Else If n<=t^. data Then Ins. Tree(n, t^. left) Else Ins. Tree(n, t^. right); End;

Деревья Процедура вывода значений элементов двоичного дерева на экран (полный обход дерева) При обходе дерева его отдельные вершины посещаются в определенном порядке. Вывод двоичного дерева можно производить рекурсивно, выполняя для каждой вершины три действия: • вывод числа, хранящегося в узле; • обход левого поддерева; • обход правого поддерева. Порядок выполнения этих действий определяет способ обхода. Способы вывода: • прямой вывод (сверху вниз); • обратный вывод (слева направо); • концевой вывод (снизу вверх).

Деревья Процедура вывода значений элементов двоичного дерева на экран (полный обход дерева) Procedure Print. Tree(t: treelink); Begin If t<>NIL Then Begin Print. Tree(t^. left); Write(t^. data: 3); Print. Tree(t^. right) End; Задание Написать процедуры прямого и концевого вывода значений элементов дерева.

Деревья Основная программа Begin Writeln( 'окончание ввода — О'); kd: =Nil; Read(Digit); While Digit<>0 Do Begin Ins. Tree(Digit, kd); Writeln('введите очередное число'); Read(Digit); End; Print. Tree(kd); End. Переменные 1) nd: treelink — значение указателя на корень дерева; 2) Digit: integer - для хранения очередного введенного числа.

Деревья Задачи 1. 2. 3. 4. 5. Описать рекурсивную логическую функцию, проверяющую наличие заданного числа в сформированном дереве. Описать рекурсивную числовую функцию, подсчитывающую сумму элементов дерева. Описать функцию, которая находит наибольший элемент непустого дерева. Описать рекурсивно и нерекурсивно логическую Функцию, входными параметрами которой являются Два дерева, проверяющую на равенство эти деревья. Описать логическую функцию, проверяющую, есть ли в непустом дереве хотя бы два одинаковых элемента.

Деревья ¡ ¡ В дереве поиска можно найти место каждого элемента, двигаясь от корня и переходя на левое или правое поддерево в зависимости от значений встречающихся данных. Использование деревьев поиска значительно сокращает время решения задачи. В среднем для нахождения элемента в списке нужно просмотреть половину списка, то есть если в списке N элементов, то надо выполнить N2 сравнений. Для поиска же заданного элемента в дереве при его правильной организации может потребоваться не более log 2 N сравнений.

Деревья Сформировать идеально сбалансированное дерево, элементами которого являются N чисел, вводимых с клавиатуры (для каждой его вершины количество вершин в левом и правом поддереве различаются не более чем на 1) Идеально сбалансированное дерево: узлы в процессе построения должны распределяться равномерно. Правило равномерного распределения узлов при известном их числе: ¡ ¡ ¡ Взять один узел в качестве корня. Построить левое поддерево с числом узлов n 1=N div 2 тем же способом. Построить правое поддерево с числом узлов n 2=N—n 1— 1 тем же способом.

Деревья Формирование идеально сбалансированного дерева {описание типов и переменных} Program Example_85; Uses Crt; Type Pt=^Node; Node=Record Data: Integer; Left, Right: Pt; End; Var n: Integer; kd: Pt; f: text;

Деревья Формирование идеально сбалансированного дерева {подпрограмма-функция формирования дерева} Function Tree(n: Integer): pt; Var newnode: pt; x, n 1, n 2: Integer; Begin If n=0 Then Tree: =nil Else Begin n 1: =n Div 2; n 2: =n—n 1 -1; Read({f, }x); New(newnode); With newnode^ Do Begin Data: =x; Left: =Tree(n 1); Right: =Tree(n 2); End; Tree: =newnode; End;

Деревья Формирование идеально сбалансированного дерева {подпрограмма – процедура вывода дерева} Procedure Print. Tree(t: pt; h: Integer); Var i: Integer; Begin If t<> Nil Then With t^ Do Begin Print. Tree(left, h+1); For i: = 1 To h Do Write(' Writeln(Data: 6); Print. Tree(Right, h+1); End; ‘);

Деревья Формирование идеально сбалансированного дерева {основная программа} Begin {Clrscr; Assign(f, ‘. f. txt'); Reset(f); } Write('n='); Readln(n); kd: =tree(n); printtree(kd, 0); Readln; End.

Деревья Результат работы программы

Деревья Результат работы программы

Деревья Поиск и включение элемента в дерево Задана последовательность слов. Определить частоту вхождения каждого из слов в последовательность. Для решения задачи любое слово ищется в дереве, которое на начальном этапе пусто. Если слово найдено, то счетчик его вхождений увеличивается на единицу, если нет, то слово включается в дерево с единичным значением счетчика. Эта задача называется задачей поиска по дереву с включением. ¡

Деревья Задача поиска по дереву с включением {описание типов и переменных} Program Example_85; Type Words=^Wordtree; Wordtree=Record data: String; k: Integer; left, right: Words; End; Var n: integer; kd: Words; x: String; f: text;

Деревья Задача поиска по дереву с включением {подпрограмма-процедура формирования дерева } Procedure Tree(x: String; Var p: Words); Begin If p=Nil Then Begin New(p); With p^ Do Begin k: =1; Data: =x; Left: =Nil; Right: =Nil; End Else If x>p^. Data Then Tree(x, p^. Left) Else If x

Деревья Формирование идеально сбалансированного дерево {подпрограмма – процедура вывода дерева} Procedure Print. Tree(t: Words; h: Integer); Var i: Integer; Begin If t<> nil Then With t^ Do Begin Print. Tree(Left, h + 1); For i: =1 To h Do Write(' '); Writeln(data, ', (', k, ')'); Print. Tree(Right, h+ 1); End;

Деревья Формирование идеально сбалансированного дерево {основная программа} Begin Assign(f, 'f. dan'); Reset(f); Write('n='); Readln(n); kd: =Nil; While n>0 Do Begin Read. Ln(f, x); Tree(x, kd); dec(n); End; Close(f); Print. Tree(kd, 0); Readln; End. Назначение n ?

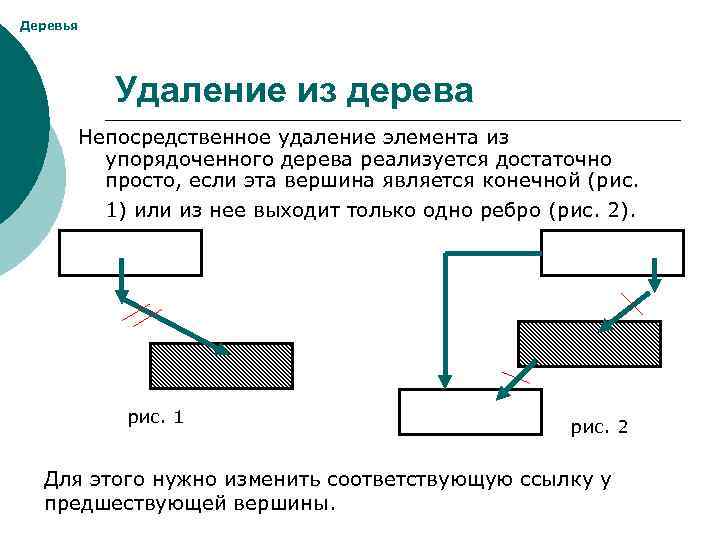Деревья Удаление из дерева Непосредственное удаление элемента из упорядоченного дерева реализуется достаточно просто, если эта вершина является конечной (рис. 1) или из нее выходит только одно ребро (рис. 2). рис. 1 рис. 2 Для этого нужно изменить соответствующую ссылку у предшествующей вершины.

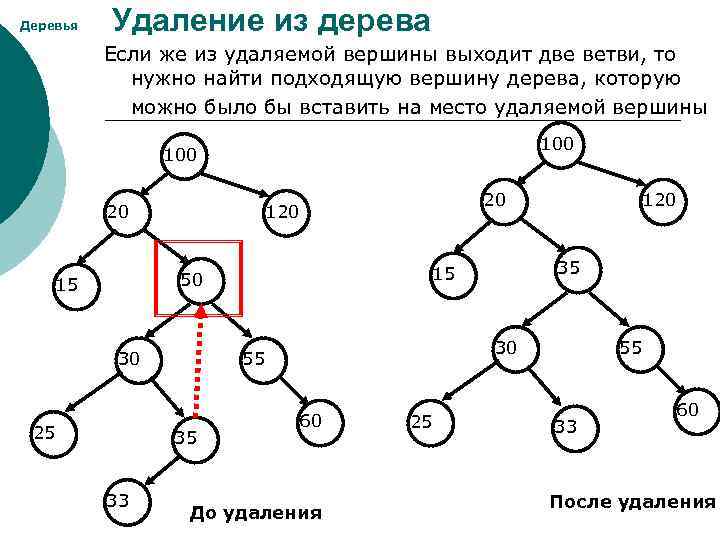Деревья Удаление из дерева Если же из удаляемой вершины выходит две ветви, то нужно найти подходящую вершину дерева, которую можно было бы вставить на место удаляемой вершины 100 20 30 25 33 30 55 35 120 35 15 50 15 20 120 60 До удаления 25 55 33 60 После удаления

Деревья Вывод Процедура удаления элемента из дерева должна различать три случая: 1. удаляемая вершина имеет два поддерева (В этом случае удаляемый элемент нужно заменить либо на самый правый элемент его левого поддерева, либо на самый левый элемент его правого поддерева. При этом они должны иметь не больше одного потомка); 2. удаляемая вершина имеет не более одного поддерева (0 или 1); 3. удаляемой вершины в дереве нет.

Деревья Удаление из дерева ¡ ¡ ¡ Рекурсивная процедура deltree, решающая поставленную задачу. Она отыскивает элемент с заданным ключом и удаляет его. В процедуре deltree описана вспомогательная процедура dl, которая работает только в первом из трех перечисленных случаев. Вспомогательная процедура dl "движется" по правой ветви левого поддерева исключаемого элемента q^ и заменяет значение ключа в q^ на соответствующее значение из самого правого элемента r^ левого поддерева.

Деревья Удаление из дерева Type Pt=^Node; Node = Record Data : Integer; Left, Right: Pt; End; Procedure Del. Tree(x: Integer; Var p: Pt); Var q: Pt; Procedure Dl(Var r: Pt); Begin If r^. Right<>Nil Then dl(r^. Right) Else Begin q^. Data: =r^. Data; q: =r; r: =r^. Left; Dispose(q); End;

Деревья Удаление из дерева Begin If p=Nil Then Writeln (' Элемента с ключом ‘x, ‘в дереве нет. ') Else If x< p^. Data Then Del. Tree(x, p^. Left) Else If x>p^. Data Then Del. Tree(x, p^. Right) Else Begin g: =p; If q^. Right=Nil Then Begin p: =q^. Left; Dispose(q) End Else If q^. Left=Nil Then Begin p: =q^. Right; Dispose(q) End Else Dl(q^. Left) End;

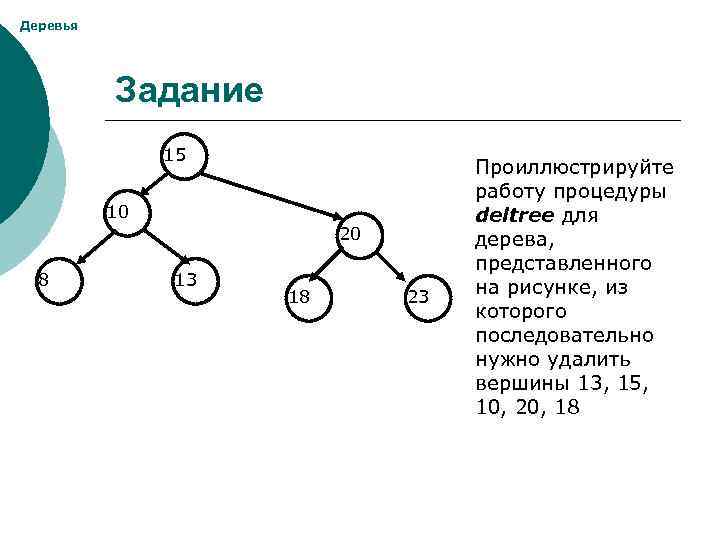Деревья Задание 15 10 20 8 13 18 23 Проиллюстрируйте работу процедуры deltree для дерева, представленного на рисунке, из которого последовательно нужно удалить вершины 13, 15, 10, 20, 18

Деревья Самостоятельно: Реализация стека при помощи массива ¡ Реализация очереди при помощи массива ¡