8d31a2888d6ece1a61f0e778a2530c2d.ppt
- Количество слайдов: 65
 DIGITAL SIGNATURES Fred Piper Codes & Ciphers Ltd 12 Duncan Road Richmond Surrey TW 9 2 JD Information Security Group Royal Holloway, University of London Egham, Surrey TW 20 0 EX Digital Signatures
DIGITAL SIGNATURES Fred Piper Codes & Ciphers Ltd 12 Duncan Road Richmond Surrey TW 9 2 JD Information Security Group Royal Holloway, University of London Egham, Surrey TW 20 0 EX Digital Signatures
 Outline 1. Brief Introduction to Cryptography 2. Public Key Systems 3. Basic Principles of Digital Signatures 4. Public Key Algorithms 5. Signing Processes 6. Arbitrated Signatures 7. Odds and Ends NOTE: We will not cover all the sections Digital Signatures 2
Outline 1. Brief Introduction to Cryptography 2. Public Key Systems 3. Basic Principles of Digital Signatures 4. Public Key Algorithms 5. Signing Processes 6. Arbitrated Signatures 7. Odds and Ends NOTE: We will not cover all the sections Digital Signatures 2
 The Essence of Security – Recognition of those you know – Introduction to those you don’t know – Written signature – Private conversation Digital Signatures 3
The Essence of Security – Recognition of those you know – Introduction to those you don’t know – Written signature – Private conversation Digital Signatures 3
 The Challenge • Transplant these basic social mechanisms to the telecommunications and/or business environment. Digital Signatures 4
The Challenge • Transplant these basic social mechanisms to the telecommunications and/or business environment. Digital Signatures 4
 The Security Issues • Sender – Am I happy that the whole world sees this ? – Am I prepared to pay to stop them ? – Am I allowed to stop them ? • Recipient – Do I have confidence in : – the originator – the message contents and message stream – no future repudiation. • Network Manager – Do I allow this user on to the network ? – How do I control their privileges ? Digital Signatures 5
The Security Issues • Sender – Am I happy that the whole world sees this ? – Am I prepared to pay to stop them ? – Am I allowed to stop them ? • Recipient – Do I have confidence in : – the originator – the message contents and message stream – no future repudiation. • Network Manager – Do I allow this user on to the network ? – How do I control their privileges ? Digital Signatures 5
 Cryptography is used to provide: 1. Secrecy 2. Data Integrity 3. User Verification 4. Non-Repudiation Digital Signatures 6
Cryptography is used to provide: 1. Secrecy 2. Data Integrity 3. User Verification 4. Non-Repudiation Digital Signatures 6
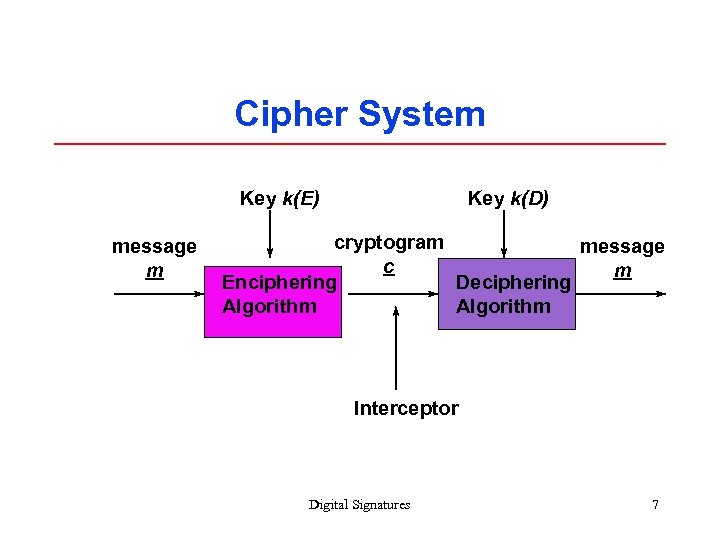 Cipher System Key k(E) message m Key k(D) cryptogram message c m Enciphering Deciphering Algorithm Interceptor Digital Signatures 7
Cipher System Key k(E) message m Key k(D) cryptogram message c m Enciphering Deciphering Algorithm Interceptor Digital Signatures 7
 The Attacker’s Perspective Unknown Key k(D) Known c Deciphering Wants m Algorithm Note: k(E) is not needed unless it helps determine k(D) Digital Signatures 8
The Attacker’s Perspective Unknown Key k(D) Known c Deciphering Wants m Algorithm Note: k(E) is not needed unless it helps determine k(D) Digital Signatures 8
 Two Types of Cipher System • Conventional or Symmetric – k(D) easily obtained from k(E) • Public or Asymmetric – Computationally infeasible to determine k(D) from k(E) Digital Signatures 9
Two Types of Cipher System • Conventional or Symmetric – k(D) easily obtained from k(E) • Public or Asymmetric – Computationally infeasible to determine k(D) from k(E) Digital Signatures 9
 • THE SECURITY OF THE SYSTEM IS DEPENDENT ON THE SECURITY OF THE KEYS Digital Signatures 10
• THE SECURITY OF THE SYSTEM IS DEPENDENT ON THE SECURITY OF THE KEYS Digital Signatures 10
 Public Key Systems • Original Concept • For a public key system an enciphering algorithm is agreed and each would-be receiver publishes the key which anyone may use to send a message to him. • Thus for a public key system to be secure it must not be possible to deduce the message from a knowledge of the cryptogram and the enciphering key. Once such a system is set up, a directory of all receivers plus their enciphering keys is published. However, the only person to know any given receiver’s deciphering key is the receiver himself. Digital Signatures 11
Public Key Systems • Original Concept • For a public key system an enciphering algorithm is agreed and each would-be receiver publishes the key which anyone may use to send a message to him. • Thus for a public key system to be secure it must not be possible to deduce the message from a knowledge of the cryptogram and the enciphering key. Once such a system is set up, a directory of all receivers plus their enciphering keys is published. However, the only person to know any given receiver’s deciphering key is the receiver himself. Digital Signatures 11
 Public Key Systems • For a public key system, encipherment must be a ‘one-way function’ which has a ‘trapdoor’. The trapdoor must be a secret known only to the receiver. • A ‘one-way function’ is one which is easy to perform but very difficult to reverse. A ‘trapdoor’ is a trick or another function which makes it easy to reverse the function Digital Signatures 12
Public Key Systems • For a public key system, encipherment must be a ‘one-way function’ which has a ‘trapdoor’. The trapdoor must be a secret known only to the receiver. • A ‘one-way function’ is one which is easy to perform but very difficult to reverse. A ‘trapdoor’ is a trick or another function which makes it easy to reverse the function Digital Signatures 12
 Some Mathematical One-Way Functions 1. 2. 3. 4. Multiplication of two large primes. Exponentiation modulo n ( n = pq ). x ax in GF(2 n) or GF(p). k Ek(m) for fixed m where Ek is encryption in a symmetric key system which is secure against known plaintext attacks. 5. x a. x where x is an n-bit binary vector and a is a fixed n-tuple of integers. Thus a. x is an integer. Digital Signatures 13
Some Mathematical One-Way Functions 1. 2. 3. 4. Multiplication of two large primes. Exponentiation modulo n ( n = pq ). x ax in GF(2 n) or GF(p). k Ek(m) for fixed m where Ek is encryption in a symmetric key system which is secure against known plaintext attacks. 5. x a. x where x is an n-bit binary vector and a is a fixed n-tuple of integers. Thus a. x is an integer. Digital Signatures 13
 Public Key Cryptosystems – Enable secure communications without exchanging secret keys – Enable 3 rd party authentication ( digital signature ) – Use number theoretic techniques – Introduce a whole new set of problems – Are extremely ingenious. Digital Signatures 14
Public Key Cryptosystems – Enable secure communications without exchanging secret keys – Enable 3 rd party authentication ( digital signature ) – Use number theoretic techniques – Introduce a whole new set of problems – Are extremely ingenious. Digital Signatures 14
 Digital Signatures • According to ISO, the term Digital Signature is used: ‘to indicate a particular authentication technique used to establish the origin of a message in order to settle disputes of what message (if any) was sent’. Digital Signatures 15
Digital Signatures • According to ISO, the term Digital Signature is used: ‘to indicate a particular authentication technique used to establish the origin of a message in order to settle disputes of what message (if any) was sent’. Digital Signatures 15
 Digital Signatures A signature on a message is some data that • validates a message and verifies its origin • a receiver can keep as evidence • a third party can use to resolve disputes. It should be It depends on u easy to compute • the message (by one person only) • a secret parameter only u easy to verify available to the sender u difficult to forge Digital Signatures 16
Digital Signatures A signature on a message is some data that • validates a message and verifies its origin • a receiver can keep as evidence • a third party can use to resolve disputes. It should be It depends on u easy to compute • the message (by one person only) • a secret parameter only u easy to verify available to the sender u difficult to forge Digital Signatures 16
 Digital Signature • • Cryptographic checksum Identifies sender Provides integrity check for data Can be checked by third party Digital Signatures 17
Digital Signature • • Cryptographic checksum Identifies sender Provides integrity check for data Can be checked by third party Digital Signatures 17
 Hand-Written Signatures • • Intrinsic to signer Same on all documents Physically attached to message Beware plastic cards. Digital Signatures • Use of secret parameter • Message dependent. Digital Signatures 18
Hand-Written Signatures • • Intrinsic to signer Same on all documents Physically attached to message Beware plastic cards. Digital Signatures • Use of secret parameter • Message dependent. Digital Signatures 18
 Principle of Digital Signatures • • There is a (secret) number which: Only one person can use Is used to identify that person ‘Anyone’ can verify that it has been used NB: Anyone who knows the value of a number can use that number. Digital Signatures 19
Principle of Digital Signatures • • There is a (secret) number which: Only one person can use Is used to identify that person ‘Anyone’ can verify that it has been used NB: Anyone who knows the value of a number can use that number. Digital Signatures 19
 Attacks on Digital Signature Schemes To impersonate A, I must either • obtain A’s private key • substitute my public key for A’s NB: Similar attacks if A is receiving secret data encrypted with A’s public key Digital Signatures 20
Attacks on Digital Signature Schemes To impersonate A, I must either • obtain A’s private key • substitute my public key for A’s NB: Similar attacks if A is receiving secret data encrypted with A’s public key Digital Signatures 20
 Obtaining a Private Key · Mathematical attacks · Physical attacks NB: It may be sufficient to obtain a device which contains the key. Knowledge of actual value is not needed. Digital Signatures 21
Obtaining a Private Key · Mathematical attacks · Physical attacks NB: It may be sufficient to obtain a device which contains the key. Knowledge of actual value is not needed. Digital Signatures 21
 Certification Authority AIM : To guarantee the authenticity of public keys. METHOD : The Certification Authority guarantees the authenticity by signing a certificate containing user’s identity and public key with its secret key. REQUIREMENT : All users must have an authentic copy of the Certification Authority’s public key. Digital Signatures 22
Certification Authority AIM : To guarantee the authenticity of public keys. METHOD : The Certification Authority guarantees the authenticity by signing a certificate containing user’s identity and public key with its secret key. REQUIREMENT : All users must have an authentic copy of the Certification Authority’s public key. Digital Signatures 22
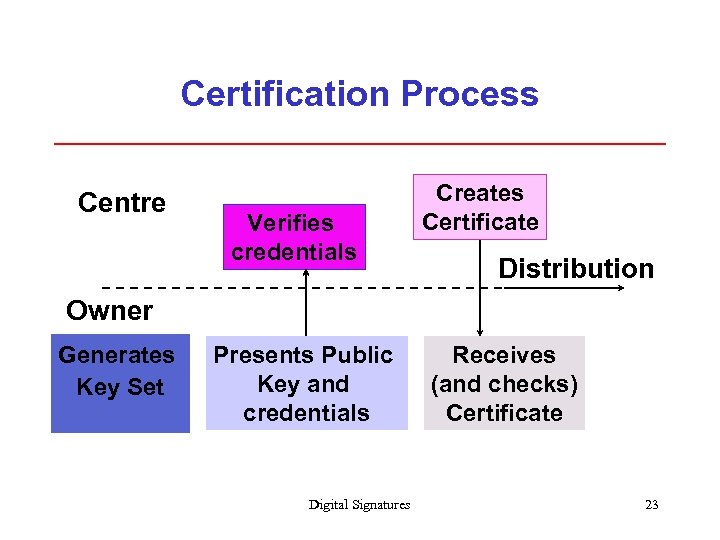 Certification Process Centre Verifies credentials Creates Certificate Distribution Owner Generates Key Set Presents Public Key and credentials Digital Signatures Receives (and checks) Certificate 23
Certification Process Centre Verifies credentials Creates Certificate Distribution Owner Generates Key Set Presents Public Key and credentials Digital Signatures Receives (and checks) Certificate 23
 How Does it Work? The CA certifies that Fred Piper’s public key is………. . Electronically signed by the CA • The Certificate can accompany all Fred’s messages • The recipient must directly or indirectly: • Trust the CA • Validate the certificate Digital Signatures 24
How Does it Work? The CA certifies that Fred Piper’s public key is………. . Electronically signed by the CA • The Certificate can accompany all Fred’s messages • The recipient must directly or indirectly: • Trust the CA • Validate the certificate Digital Signatures 24
 User Authentication Certificates • Ownership of certificate does not establish identity • Need protocols establishing use of corresponding secret keys Digital Signatures 25
User Authentication Certificates • Ownership of certificate does not establish identity • Need protocols establishing use of corresponding secret keys Digital Signatures 25
 WARNING • Identity Theft • You ‘are’ your private key • You ‘are’ the private key corresponding to the public key in your certificiate Digital Signatures 26
WARNING • Identity Theft • You ‘are’ your private key • You ‘are’ the private key corresponding to the public key in your certificiate Digital Signatures 26
 Certification Authorities • • • Problems/Questions Who generates users’ keys? How is identity established? How can certificates be cancelled? Any others? Digital Signatures 27
Certification Authorities • • • Problems/Questions Who generates users’ keys? How is identity established? How can certificates be cancelled? Any others? Digital Signatures 27
 Fundamental Requirement Internal infrastructure to support secure technological implementation Digital Signatures 28
Fundamental Requirement Internal infrastructure to support secure technological implementation Digital Signatures 28
 Is everything OK? Announcement in Microsoft Security Bulletin MS 01 -017 “Veri. Sign Inc recently advised Microsoft that on January 29 -30 2001 it issued two Veri. Sign Class 3 codesigning digital certificates to an individual who fraudulently claimed to be a Microsoft employee. ” Digital Signatures 29
Is everything OK? Announcement in Microsoft Security Bulletin MS 01 -017 “Veri. Sign Inc recently advised Microsoft that on January 29 -30 2001 it issued two Veri. Sign Class 3 codesigning digital certificates to an individual who fraudulently claimed to be a Microsoft employee. ” Digital Signatures 29
 RSA System • Publish integers n and e where n = pq (p and q large primes) and e is chosen so that (e, (p-1)(q-1)) = 1. • If message is an integer m with 0 < m < n the cryptogram c = me (mod n). • The primes p and q are ‘Secret’ (i. e. known only to the receiver) and the system’s security depends on the fact that knowledge of n will not enable the interceptor to work out p and q. Digital Signatures 30
RSA System • Publish integers n and e where n = pq (p and q large primes) and e is chosen so that (e, (p-1)(q-1)) = 1. • If message is an integer m with 0 < m < n the cryptogram c = me (mod n). • The primes p and q are ‘Secret’ (i. e. known only to the receiver) and the system’s security depends on the fact that knowledge of n will not enable the interceptor to work out p and q. Digital Signatures 30
 RSA System Since (e, (p-1)(q-1)) = 1 there is an integer d such that ed = 1(mod(p-1)(q-1)). [NOTE: without knowing p and q it is ‘impossible’ to determine d. ] To decipher raise c to the power d. Then m=cd (=med) (mod n). System works because if n=pq, ak(p-1)(q-1) + 1 = a (mod n) for all a, k. Digital Signatures 31
RSA System Since (e, (p-1)(q-1)) = 1 there is an integer d such that ed = 1(mod(p-1)(q-1)). [NOTE: without knowing p and q it is ‘impossible’ to determine d. ] To decipher raise c to the power d. Then m=cd (=med) (mod n). System works because if n=pq, ak(p-1)(q-1) + 1 = a (mod n) for all a, k. Digital Signatures 31
 RSA Summary and Example Theory n = p. q e. d 1(mod(p-1) (q-1)) Public key is (e, n) Private key is (d, n) Message M (0 < M < n) Choice 2773 = 47. 59 p=47 q=59 17. 157 ≡ 1(mod 2668) e=17 d=157 (17, 2773) (157, 2773) M = 31 NB : Knowledge of p and q is required to compute d. Encryption using Private Key : C ≡ Me (mod n) 587 ≡ 3117 (mod 2773) Decryption using Private Key : M ≡ Cd (mod n) 31 ≡ 587157 (mod 2773) Digital Signatures 32
RSA Summary and Example Theory n = p. q e. d 1(mod(p-1) (q-1)) Public key is (e, n) Private key is (d, n) Message M (0 < M < n) Choice 2773 = 47. 59 p=47 q=59 17. 157 ≡ 1(mod 2668) e=17 d=157 (17, 2773) (157, 2773) M = 31 NB : Knowledge of p and q is required to compute d. Encryption using Private Key : C ≡ Me (mod n) 587 ≡ 3117 (mod 2773) Decryption using Private Key : M ≡ Cd (mod n) 31 ≡ 587157 (mod 2773) Digital Signatures 32
 El Gamal Cipher – Work in GF(q) – For practical systems • q = large prime • q = 2 n – Note: We will not define GF(2 n). For a prime q arithmetic in GF(q) is arithmetic modulo q. Digital Signatures 33
El Gamal Cipher – Work in GF(q) – For practical systems • q = large prime • q = 2 n – Note: We will not define GF(2 n). For a prime q arithmetic in GF(q) is arithmetic modulo q. Digital Signatures 33
 El Gamal Cipher System wide parameters : integers g, p NB: p is a large prime and g is a primitive element mod p. A chooses private key x such that 1 < x < p - 1 A’s public key is y = gx mod p. Note: x is called the discrete logarithm of y modulo p to the base g. Digital Signatures 34
El Gamal Cipher System wide parameters : integers g, p NB: p is a large prime and g is a primitive element mod p. A chooses private key x such that 1 < x < p - 1 A’s public key is y = gx mod p. Note: x is called the discrete logarithm of y modulo p to the base g. Digital Signatures 34
 El Gamal Encryption If B wants to send secret message m to A then 1. B obtains A’s public key y plus g and p 2. B generates random integer k. 3. B sends gk (mod p) and c = myk (mod p) to A. A uses x to compute yk from gk and then evaluates m. Digital Signatures 35
El Gamal Encryption If B wants to send secret message m to A then 1. B obtains A’s public key y plus g and p 2. B generates random integer k. 3. B sends gk (mod p) and c = myk (mod p) to A. A uses x to compute yk from gk and then evaluates m. Digital Signatures 35
 El Gamal Cipher Important facts from last slide • g is special type of number • sender needs random number generator • cryptogram is twice as long as message Digital Signatures 36
El Gamal Cipher Important facts from last slide • g is special type of number • sender needs random number generator • cryptogram is twice as long as message Digital Signatures 36
 El Gamal - Encryption - Worked Example Prime p = 23 Primitive element a = 11 Private key x = 6 Public key y = 116(mod 23) = 9 To encipher m = 10 Assume random value k = 3 ak = 113 mod 23 = 20 yk = 1118 mod 23 = 16 myk = 10. 16 mod 23 = 22 Thus transmit (20, 22) Digital Signatures 37
El Gamal - Encryption - Worked Example Prime p = 23 Primitive element a = 11 Private key x = 6 Public key y = 116(mod 23) = 9 To encipher m = 10 Assume random value k = 3 ak = 113 mod 23 = 20 yk = 1118 mod 23 = 16 myk = 10. 16 mod 23 = 22 Thus transmit (20, 22) Digital Signatures 37
 El Gamal - Worked Example To decrypt 20, 22 yk = (ak)x = 206 = 16 mod 23 To find m: solve c = myk mod p i. e. solve 22 = m 16 mod 23 Solution m = 10 Digital Signatures 38
El Gamal - Worked Example To decrypt 20, 22 yk = (ak)x = 206 = 16 mod 23 To find m: solve c = myk mod p i. e. solve 22 = m 16 mod 23 Solution m = 10 Digital Signatures 38
 Modular Exponentiation • Both RSA and El Gamal involve computing xa (mod N) for large x, a and N • To speed up process need: • Fast multiplication algorithm • Avoid intermediate values becoming too large • Limit number of modular multiplications Digital Signatures 39
Modular Exponentiation • Both RSA and El Gamal involve computing xa (mod N) for large x, a and N • To speed up process need: • Fast multiplication algorithm • Avoid intermediate values becoming too large • Limit number of modular multiplications Digital Signatures 39
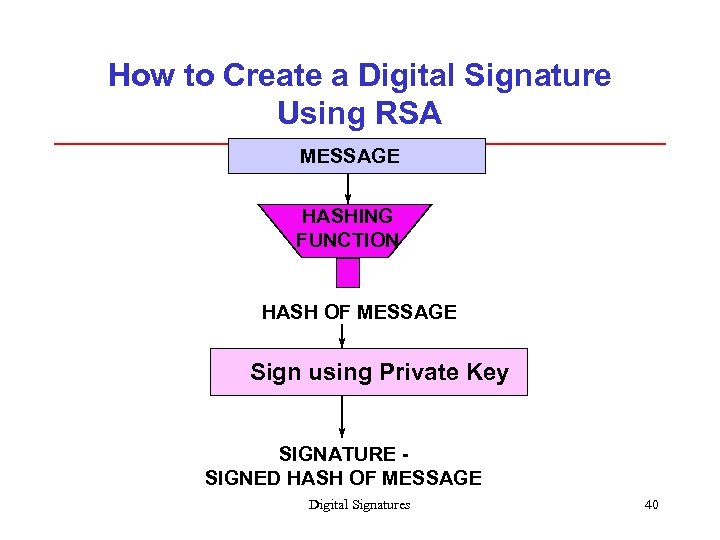 How to Create a Digital Signature Using RSA MESSAGE HASHING FUNCTION HASH OF MESSAGE Sign using Private Key SIGNATURE SIGNED HASH OF MESSAGE Digital Signatures 40
How to Create a Digital Signature Using RSA MESSAGE HASHING FUNCTION HASH OF MESSAGE Sign using Private Key SIGNATURE SIGNED HASH OF MESSAGE Digital Signatures 40
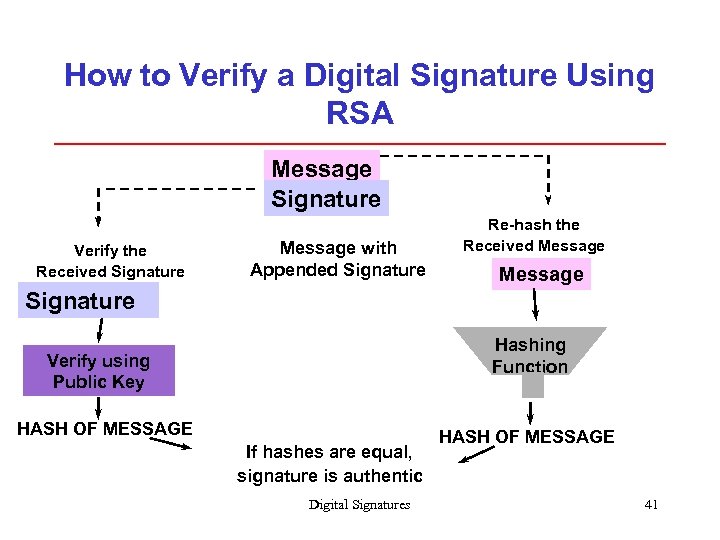 How to Verify a Digital Signature Using RSA Message Signature Verify the Received Signature Message with Appended Signature Re-hash the Received Message Signature Hashing Function Verify using Public Key HASH OF MESSAGE If hashes are equal, signature is authentic Digital Signatures HASH OF MESSAGE 41
How to Verify a Digital Signature Using RSA Message Signature Verify the Received Signature Message with Appended Signature Re-hash the Received Message Signature Hashing Function Verify using Public Key HASH OF MESSAGE If hashes are equal, signature is authentic Digital Signatures HASH OF MESSAGE 41
 Requirements for Hash Function h (H 1) condenses message M of arbitrary length into a fixed length ‘digest’ h(M) (H 2) is one-way (H 3) is collision free - it is computationally infeasible to construct messages M, M' with h(M) = h(M') H 3 implies a restriction on the size of h(M). Digital Signatures 42
Requirements for Hash Function h (H 1) condenses message M of arbitrary length into a fixed length ‘digest’ h(M) (H 2) is one-way (H 3) is collision free - it is computationally infeasible to construct messages M, M' with h(M) = h(M') H 3 implies a restriction on the size of h(M). Digital Signatures 42
 DSA • Proposed by NIST in 1991 • Explicitly requires the use of a hash function – SHA-1 • Very different set of functional capabilities than RSA Digital Signatures 43
DSA • Proposed by NIST in 1991 • Explicitly requires the use of a hash function – SHA-1 • Very different set of functional capabilities than RSA Digital Signatures 43
 DSA Set Up • System parameters – select a 160 -bit prime q – choose a 1024 -bit prime p so that q | p-1 – choose g Zp* and compute a = g(p-1)/q mod p – if a=1 repeat with different g • User keys – select random secret key x (1 x q-1) – compute public key y = ax mod p Digital Signatures 44
DSA Set Up • System parameters – select a 160 -bit prime q – choose a 1024 -bit prime p so that q | p-1 – choose g Zp* and compute a = g(p-1)/q mod p – if a=1 repeat with different g • User keys – select random secret key x (1 x q-1) – compute public key y = ax mod p Digital Signatures 44
 Signing with DSA • To sign message m – hash message m to give h(m) (1 h(m) q-1) – generate random secret k (1 k q 1) – compute r = (ak mod p) mod q – compute k-1 mod q – compute s = k-1{h(m) + ar} mod q – signature on m is (r, s) Digital Signatures 45
Signing with DSA • To sign message m – hash message m to give h(m) (1 h(m) q-1) – generate random secret k (1 k q 1) – compute r = (ak mod p) mod q – compute k-1 mod q – compute s = k-1{h(m) + ar} mod q – signature on m is (r, s) Digital Signatures 45
 DSA Signature Verification • To verify (r, s) – check that 1 r q-1 and 1 s q-1 – compute w = s-1 mod q – compute u 1 = wh(m) mod q – compute u 2 = rw mod q – accept signature if – (au 1 yu 2 mod p) mod q = r Digital Signatures 46
DSA Signature Verification • To verify (r, s) – check that 1 r q-1 and 1 s q-1 – compute w = s-1 mod q – compute u 1 = wh(m) mod q – compute u 2 = rw mod q – accept signature if – (au 1 yu 2 mod p) mod q = r Digital Signatures 46
 Security of DSA • Depends on – taking discrete logarithms in GF(p) (GNFS) – the logarithm problem in the cyclic subgroup of order q • algorithms for this take time proportional to q 1/2 • we choose q 2160 and p 21024 – other concerns follow the case of El Gamal signatures Digital Signatures 47
Security of DSA • Depends on – taking discrete logarithms in GF(p) (GNFS) – the logarithm problem in the cyclic subgroup of order q • algorithms for this take time proportional to q 1/2 • we choose q 2160 and p 21024 – other concerns follow the case of El Gamal signatures Digital Signatures 47
 Performance of DSA • Using the subgroup of order q gives good improvements over El Gamal signatures – for signature – one (partial) exponentiation mod p, all other operations less significant – also there are opportunities for pre-computation – for verification – two (partial) exponentiations mod p, all other operations less significant Digital Signatures 48
Performance of DSA • Using the subgroup of order q gives good improvements over El Gamal signatures – for signature – one (partial) exponentiation mod p, all other operations less significant – also there are opportunities for pre-computation – for verification – two (partial) exponentiations mod p, all other operations less significant Digital Signatures 48
 DSA and RSA • set a unit of time to be that required for one 1024 -bit multiplication • use e=216+1 and CRT for RSA • pre-computation with DSA not included • also a difference in the sizes of the signatures Digital Signatures 49
DSA and RSA • set a unit of time to be that required for one 1024 -bit multiplication • use e=216+1 and CRT for RSA • pre-computation with DSA not included • also a difference in the sizes of the signatures Digital Signatures 49
 Signing and Verifying • Which is more important - signature or verification performance? – depends on the application! • certificates: sign once but verify very often • secure E-mail: perhaps sign and verify once • document storage: sign once but maybe never verify Digital Signatures 50
Signing and Verifying • Which is more important - signature or verification performance? – depends on the application! • certificates: sign once but verify very often • secure E-mail: perhaps sign and verify once • document storage: sign once but maybe never verify Digital Signatures 50
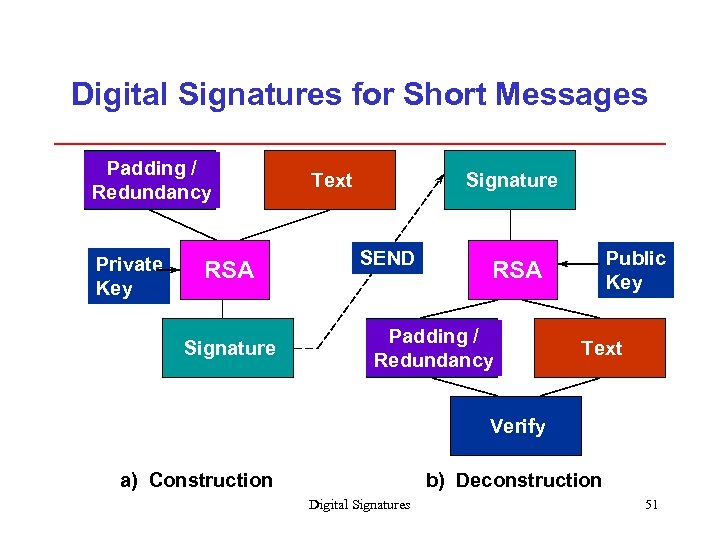 Digital Signatures for Short Messages Padding / Redundancy Private Key RSA Signature Text Signature SEND Public Key RSA Padding / Redundancy Text Verify a) Construction b) Deconstruction Digital Signatures 51
Digital Signatures for Short Messages Padding / Redundancy Private Key RSA Signature Text Signature SEND Public Key RSA Padding / Redundancy Text Verify a) Construction b) Deconstruction Digital Signatures 51
 Types of Digital Signature 1. Arbitrated Signatures Mediation by third party, the arbitrator u signing u verifying u resolving disputes 2. True Signatures Direct communication between sender and receiver Third party involved only in case of dispute Digital Signatures 52
Types of Digital Signature 1. Arbitrated Signatures Mediation by third party, the arbitrator u signing u verifying u resolving disputes 2. True Signatures Direct communication between sender and receiver Third party involved only in case of dispute Digital Signatures 52
 Arbitrated Signatures Require trusted arbitrator • Arbitrator is involved in – Signing process – Settlement of all disputes – No one else can settle disputes – Potential bottleneck Digital Signatures 53
Arbitrated Signatures Require trusted arbitrator • Arbitrator is involved in – Signing process – Settlement of all disputes – No one else can settle disputes – Potential bottleneck Digital Signatures 53
 Example of Arbitrated Signature Scheme (1) Requirement: A wants to send B message B wants assurance of contents, that A was originator and that A cannot deny either fact. Assumption: A and B agree to trust an arbitrator (ARB) and to accept ARB’s decision as binding. Digital Signatures 54
Example of Arbitrated Signature Scheme (1) Requirement: A wants to send B message B wants assurance of contents, that A was originator and that A cannot deny either fact. Assumption: A and B agree to trust an arbitrator (ARB) and to accept ARB’s decision as binding. Digital Signatures 54
 Example of Arbitrated Signature Scheme (2) Cryptographic Assumption 1. Will use symmetric Algorithm eg DES 2. Will use MACs 3. A has established a DES key KA shared with ARB 4. B has established a DES key KB shared with ARB Digital Signatures 55
Example of Arbitrated Signature Scheme (2) Cryptographic Assumption 1. Will use symmetric Algorithm eg DES 2. Will use MACs 3. A has established a DES key KA shared with ARB 4. B has established a DES key KB shared with ARB Digital Signatures 55
 Example of Arbitrated Signature Scheme (3) A wants to send ‘signed’ message M to B Simplified protocol 1) A ARB : M 1=M || MACKA 2) ARB uses KA to check MACKA 3) ARB B : M 2 = M 1|| MACKB 4) B uses KB to check MACKB Note: B has no way of checking MACKA is correct. May be necessary to include identities in messages. Digital Signatures 56
Example of Arbitrated Signature Scheme (3) A wants to send ‘signed’ message M to B Simplified protocol 1) A ARB : M 1=M || MACKA 2) ARB uses KA to check MACKA 3) ARB B : M 2 = M 1|| MACKB 4) B uses KB to check MACKB Note: B has no way of checking MACKA is correct. May be necessary to include identities in messages. Digital Signatures 56
 True Signature Requirement • Only one person can sign but anyone can verify the signature Public Key Requirement • Anyone can encrypt a message but only one person can decrypt the cryptogram. Digital Signatures 57
True Signature Requirement • Only one person can sign but anyone can verify the signature Public Key Requirement • Anyone can encrypt a message but only one person can decrypt the cryptogram. Digital Signatures 57
 True Signature It is ‘natural’ to try to adopt public key systems to produce signature schemes by using the secret key in the signing process Digital Signatures 58
True Signature It is ‘natural’ to try to adopt public key systems to produce signature schemes by using the secret key in the signing process Digital Signatures 58
 Digital Signatures Common Terminology identifies the terms Digital Signature and True Signature Digital Signatures 59
Digital Signatures Common Terminology identifies the terms Digital Signature and True Signature Digital Signatures 59
 The Decision Process • • Do I need Cryptography? Do I need Public Key Cryptography? Do I need PKI? How do I establish a PKI? Digital Signatures 60
The Decision Process • • Do I need Cryptography? Do I need Public Key Cryptography? Do I need PKI? How do I establish a PKI? Digital Signatures 60
 Often Heard • • PKI has never really taken off PKI is dead I’ve got a PKI, what do I do with it? Secure e-commerce needs PKI Digital Signatures 61
Often Heard • • PKI has never really taken off PKI is dead I’ve got a PKI, what do I do with it? Secure e-commerce needs PKI Digital Signatures 61
 Diffie Hellman Key Establishment Protocol General Idea: Use Public System A and B exchange public keys: PA and PB There is a publicly known function f which has 2 numbers as input and one number as output. A computes f (SA, PB) where SA is A’s private key B computes f (SB, PA) where SB is B’s private key f is chosen so that f (SA, PB) = f (SB, PA) So A and B now share a (secret) number Digital Signatures 62
Diffie Hellman Key Establishment Protocol General Idea: Use Public System A and B exchange public keys: PA and PB There is a publicly known function f which has 2 numbers as input and one number as output. A computes f (SA, PB) where SA is A’s private key B computes f (SB, PA) where SB is B’s private key f is chosen so that f (SA, PB) = f (SB, PA) So A and B now share a (secret) number Digital Signatures 62
 Diffie Hellman Key Establishment Protocol For the mathematicians: Agree: Prime p primitive element a A : chooses random r. A and sends B : chooses random r. B and sends Key: Clearly any interceptor who can find discrete logarithms can break the scheme In this case Note: Comparison with El Gamal Digital Signatures 63
Diffie Hellman Key Establishment Protocol For the mathematicians: Agree: Prime p primitive element a A : chooses random r. A and sends B : chooses random r. B and sends Key: Clearly any interceptor who can find discrete logarithms can break the scheme In this case Note: Comparison with El Gamal Digital Signatures 63
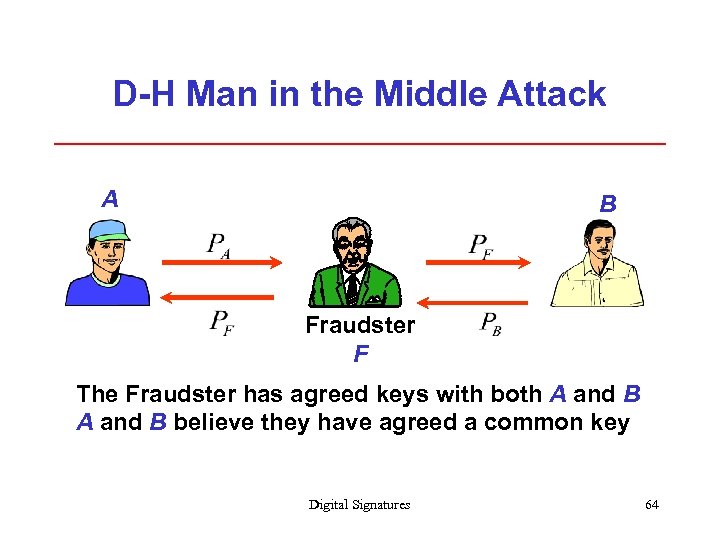 D-H Man in the Middle Attack A B Fraudster F The Fraudster has agreed keys with both A and B believe they have agreed a common key Digital Signatures 64
D-H Man in the Middle Attack A B Fraudster F The Fraudster has agreed keys with both A and B believe they have agreed a common key Digital Signatures 64
 D-H Man-in-the-Middle Attack For the mathematicians A B Fraudster F The Fraudster has agreed keys with both A and B believe they have agreed a common key Digital Signatures 65
D-H Man-in-the-Middle Attack For the mathematicians A B Fraudster F The Fraudster has agreed keys with both A and B believe they have agreed a common key Digital Signatures 65


