Digital Electronics Chap 1 The Start of

Digital Electronics Chap 1

The Start of the Modern Electronics Era Bardeen, Shockley, and Brattain at Bell Labs - Brattain and Bardeen invented the bipolar transistor in 1947. The first germanium bipolar transistor. Roughly 50 years later, electronics account for 10% (4 trillion dollars) of the world GDP.

Electronics Milestones 1874 1906 Braun invents the solid-state rectifier. De. Forest invents triode vacuum tube. 1907 -1927 1925 1947 1952 1956 First radio circuits developed from diodes and triodes. Lilienfeld field-effect device patent filed. Bardeen and Brattain at Bell Laboratories invent bipolar transistors. Commercial bipolar transistor production at Texas Instruments. Bardeen, Brattain, and Shockley receive Nobel prize. 1958 1961 1963 1968 1970 1971 1978 1974 1984 2000 Integrated circuit developed by Kilby and Noyce First commercial IC from Fairchild Semiconductor IEEE formed from merger or IRE and AIEE First commercial IC opamp One transistor DRAM cell invented by Dennard at IBM. 4004 Intel microprocessor introduced. First commercial 1 -kilobit memory. 8080 microprocessor introduced. Megabit memory chip introduced. Alferov, Kilby, and Kromer share Nobel prize

Evolution of Electronic Devices Vacuum Tubes Discrete Transistors SSI and MSI Integrated Circuits VLSI Surface-Mount Circuits

Microelectronics Proliferation n n The integrated circuit was invented in 1958. World transistor production has more than doubled every year for the past twenty years. Every year, more transistors are produced than in all previous years combined. Approximately 109 transistors were produced in a recent year. Roughly 50 transistors for every ant in the world. *Source: Gordon Moore’s Plenary address at the 2003 International Solid State Circuits Conference.

5 Commendments n n Moore’s Law : The number of transistors on a chip doubles annually Rock’s Law : The cost of semiconductor tools doubles every four years Machrone’s Law: The PC you want to buy will always be $5000 Metcalfe’s Law : A network’s value grows proportionately to the number of its users squared

5 Commandments(cont. ) Wirth’s Law : Software is slowing faster than hardware is accelerating n Further Reading: “ 5 Commandments”, IEEE Spectrum December 2003, pp. 31 -35. n

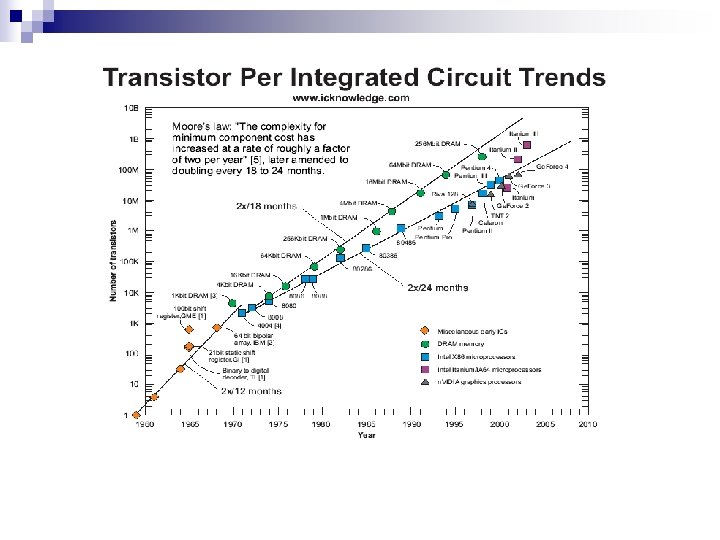
Moore’s law n n n Moore predicted that the number of transistors that can be integrated on a die would grow exponentially with time. Amazingly visionary – million transistor/chip barrier was crossed in the 1980’s. 16 M transistors (Ultra Sparc III) 140 M transistor (HP PA-8500) 1. 7 B transistor (Intel Montecito)

DEC PDP-11 CPU

HP PA 7000 RISC

Motorola 68020

Motorola 68040

Toshiba MIPS

Intel 8088

Intel 80386

80386 (cont. )

Intel 80486

Intel Pentium

Intel Pentium 4 Prescott

Penryn and Nehalem n n Penryn : 45 nm Core 2 Architecture : Core 2 Extreme QX 9650 Nehalem : Core i 7

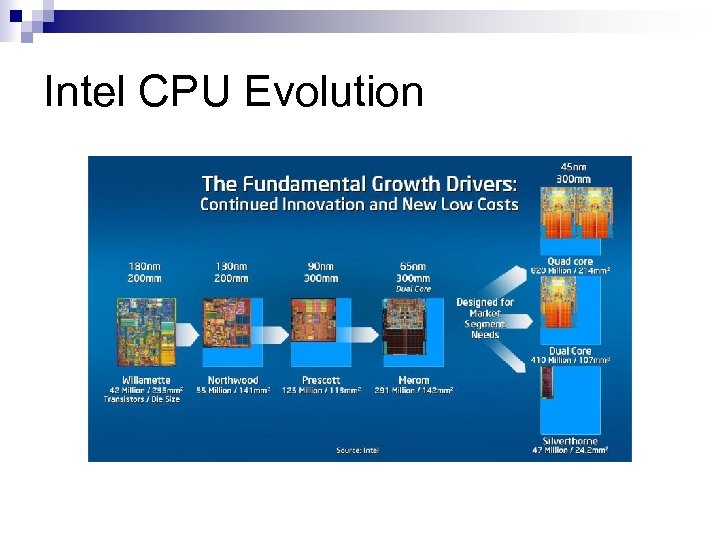Intel CPU Evolution

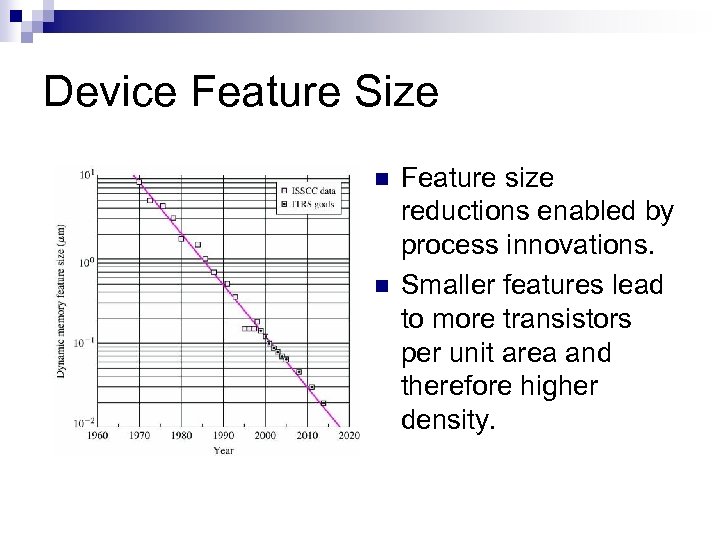Device Feature Size n n Feature size reductions enabled by process innovations. Smaller features lead to more transistors per unit area and therefore higher density.

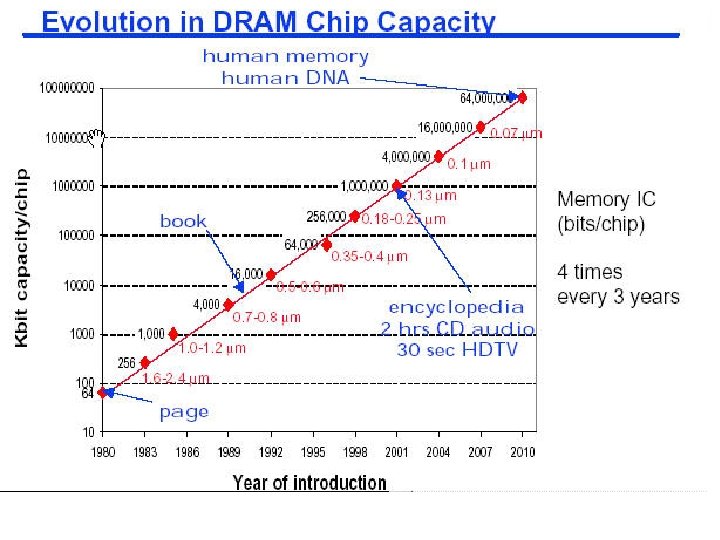
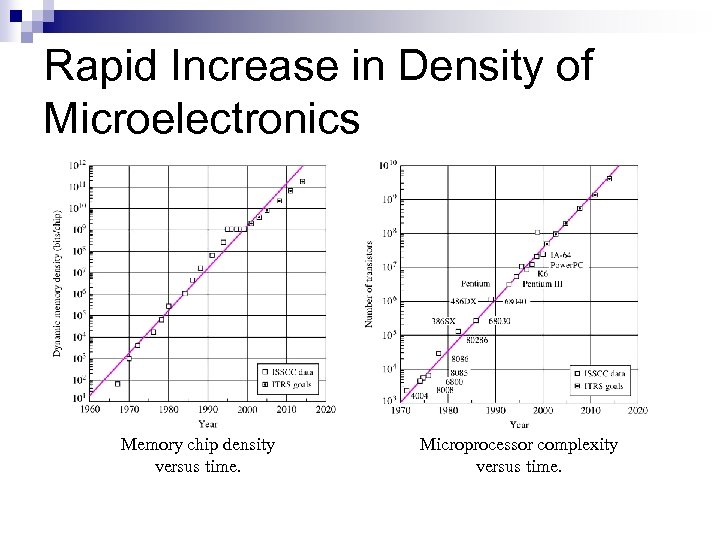Rapid Increase in Density of Microelectronics Memory chip density versus time. Microprocessor complexity versus time.

IC Design Step 1: RTL

IC Design 2 : Layout

IC Design 3 : Fabrication

IC Design 4 : Chip

IC Design 5 : System

IC design is mostly coding Hardware Description Language (Verilog, VHDL) are widely used in today’s IC design. n C programs need to obey rules set by OS. n HDL programs need to obey physical rules in the real world. n

Analog versus Digital Electronics Most observables are analog n But the most convenient way to represent and transmit information electronically is digital n Analog/digital and digital/analog conversion is essential n

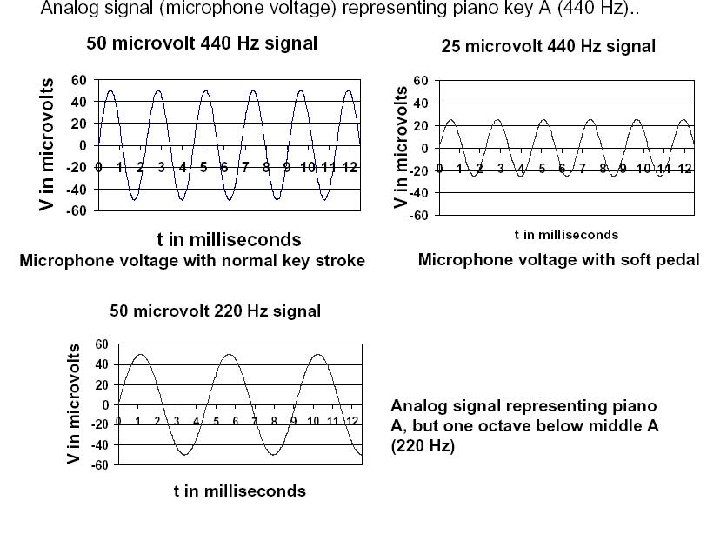
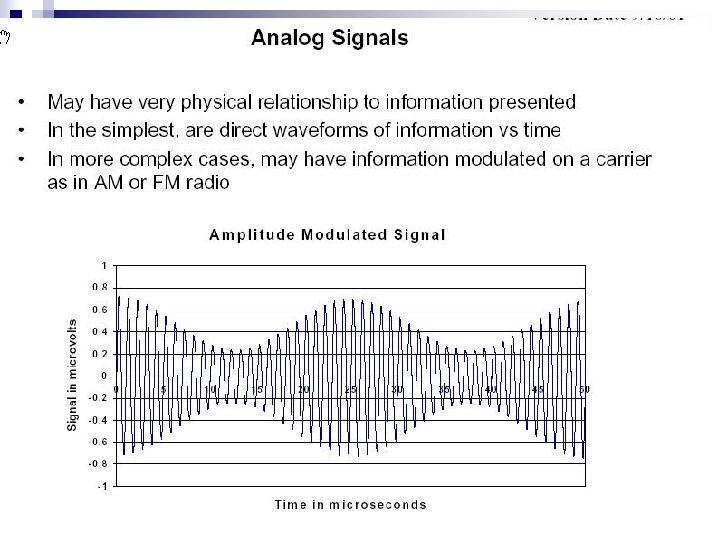
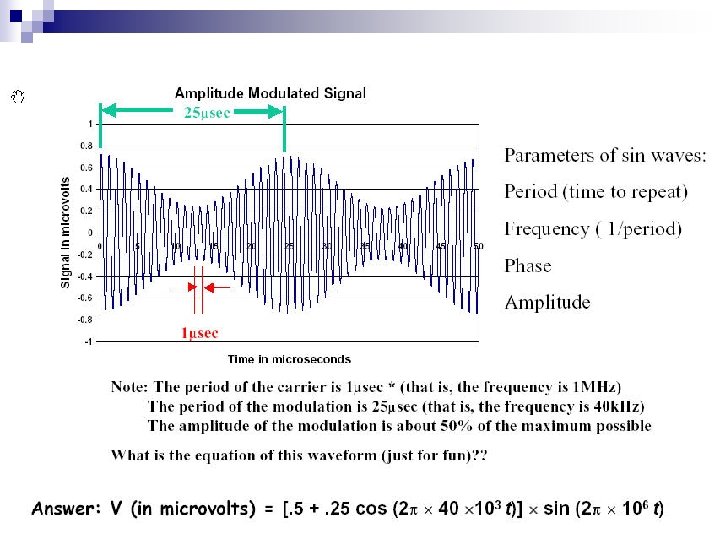
Digital signal representation n n By using binary numbers we can represent any quantity. For example a binary two (10) could represent a 2 volt signal. But we generally have to agree on some sort of “code” and the dynamic range of the signal in order to know the form and the minimum number of bits. Possible digital representation for a pure sine wave of known frequency. We must choose maximum value and “resolution” or “error, ” then we can encode the numbers. Suppose we want 1 V accuracy of amplitude with maximum amplitude of 50 V, we could use a simple pure binary code with 6 bits of information.

Digital representations of logical functions n n Digital signals also offer an effective way to execute logic. The formalism for performing logic with binary variables is called switching algebra or boolean algebra. Digital electronics combines two important properties: ¨ The ability to represent real functions by coding the information in digital form. ¨ The ability to control a system by a process of manipulation and evaluation of digital variables using switching algebra.

Digital Representations of logic functions (cont. ) n n n Digital signals can be transmitted, received, amplified, and retransmitted with no degradation. Binary numbers are a natural method of expressing logic variables. Complex logic functions are easily expressed as binary function. With digital representation, we can achieve arbitrary levels of “ dynamic range, ” that is, the ratio of the largest possible signal to the smallest than can be distinguished above the background noise. Digital information is easily and inexpensively stored

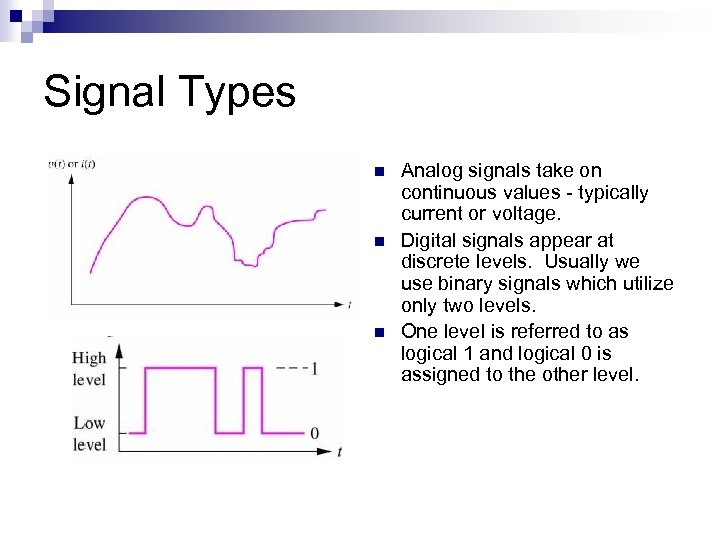Signal Types n n n Analog signals take on continuous values - typically current or voltage. Digital signals appear at discrete levels. Usually we use binary signals which utilize only two levels. One level is referred to as logical 1 and logical 0 is assigned to the other level.

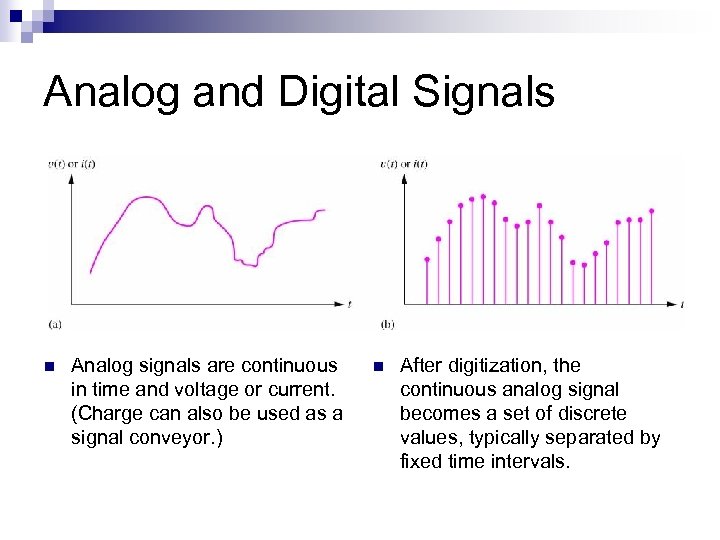Analog and Digital Signals n Analog signals are continuous in time and voltage or current. (Charge can also be used as a signal conveyor. ) n After digitization, the continuous analog signal becomes a set of discrete values, typically separated by fixed time intervals.

Digital-to-Analog (D/A) Conversion n For an n-bit D/A converter, the output voltage is expressed as: n The smallest possible voltage change is known as the least significant bit or LSB.

DAC TI’s 20 -bit sigma delta DAC

Analog-to-Digital (A/D) Conversion n Analog input voltage vx is converted to the nearest n-bit number. For a four bit converter, 0 -> vx input yields a 0000 -> 1111 digital output. Output is approximation of input due to the limited resolution of the n -bit output. Error is expressed as:

ADC Die Photo n Rockwell Scientific 4 Gsps ADC

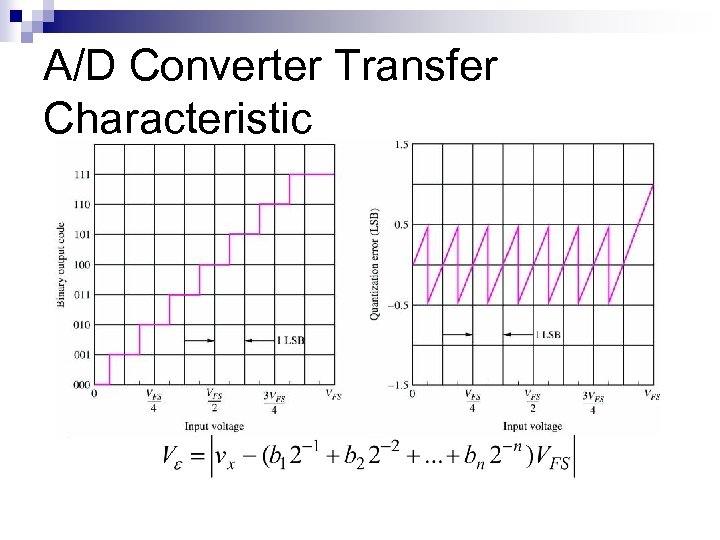A/D Converter Transfer Characteristic

Introduction to Circuit Theory n n Circuit theory is based on the concept of modeling. To analyze any complex physical system, we must be able to describe the system in terms of an idealized model that is an interconnection of idealized elements. By analyzing the circuit model, we can predict the behavior of the physical circuit and design better circuits.

Lumped Circuits Lumped circuits are obtained by connecting lumped elements. n Typical lumped elements are resistors, capacitors, inductors, and transformers. n The size of lumped circuit is small compared to the wavelength of their normal frequency of operation. n

Operating Frequency vs. Size Audio Circuit operate @ 25 Khz, the wavelength λ~=12 Km, which is much larger than the size of any elements n Computer Circuit @ 500 Mhz, λ=0. 6 m, the lumped approx. is not so good. n Microwave circuit, where λis between 10 cm to 1 mm, Kirchhoff’s laws do not apply for the cavity resonators. n

Lumped Circuit definition A lumped circuit is by definition an interconnecting lumped element. n The two terminal elements are called branches, the terminals of the elements are called nodes. n The branch voltage and branch current are the basic variables of interest in circuit theory. n

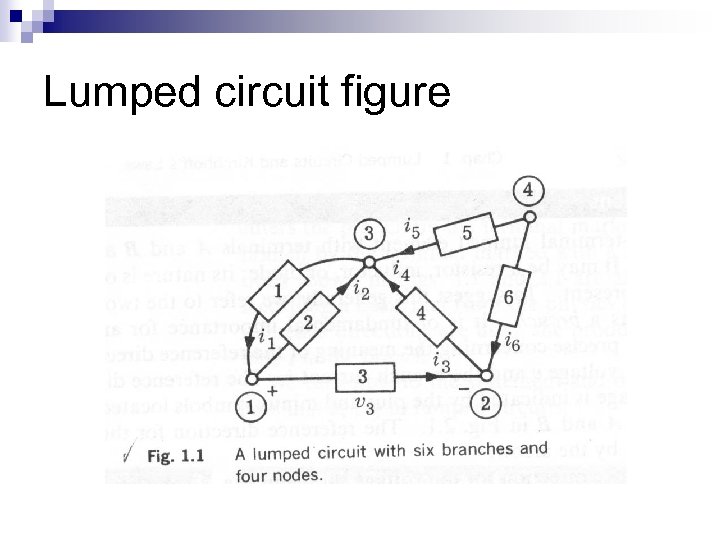Lumped circuit figure

Reference Directions n n n A two terminal lumped elements (branch) with nodes A and B. The reference directions for the branch voltage v and branch current i are shown in the graph. The reference direction is chosen arbitrarily.

Notational conventions Total quantities will be represented by lowercase letters with capital subscripts, such as v. T anf i. T. n The dc components are represented by capital letters with capital subscripts as VDC and IDC; changes or variations from the dc value are represented by vac and iac. n v. T = VDC + vac n i. T = IDC + iac n

Kirchhoff’s Current Law (KCL) n For any lumped electric circuit, for any of its nodes, and at any time, the algebraic sum of all branch currents leaving the node is zero.

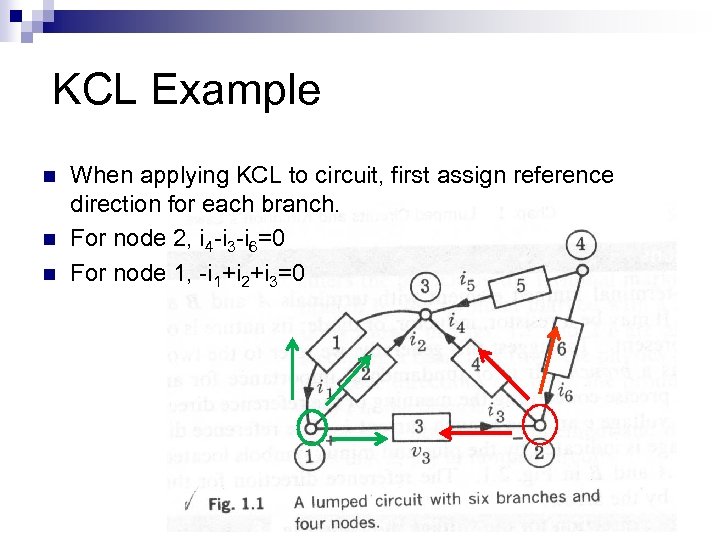KCL Example n n n When applying KCL to circuit, first assign reference direction for each branch. For node 2, i 4 -i 3 -i 6=0 For node 1, -i 1+i 2+i 3=0

Kirchhoff’s Voltage Law (KVL) n For any lumped electric circuit, for any of its loops, and at any time, the algebraic sum of the branch voltages around the loop is zero.

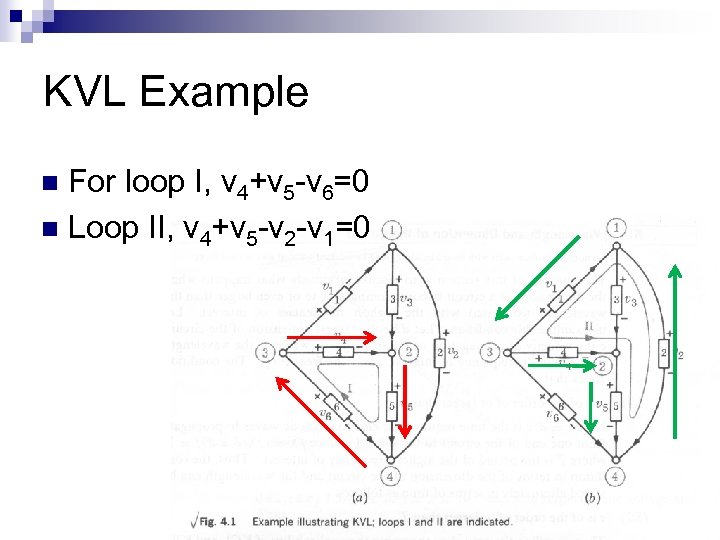KVL Example For loop I, v 4+v 5 -v 6=0 n Loop II, v 4+v 5 -v 2 -v 1=0 n

Properties of KCL and KVL KCL imposes a linear constraint on the branch currents. n KCL applies to any lumped electric circuit; it is independent of the nature of the elements. n KCL expresses the conservation of charge at any time. n

Properties of KVL and KCL (cont. ) An example where KCL doesn’t apply is the whip antenna. The antenna is about ¼ wavelength so it is not a lumped circuit. n KVL imposes a linear constraint between branch voltages of a loop. n KVL is independent of the natural of the elements. n

Circuit Elements Resistors n Independent sources n Capacitors n Inductors n

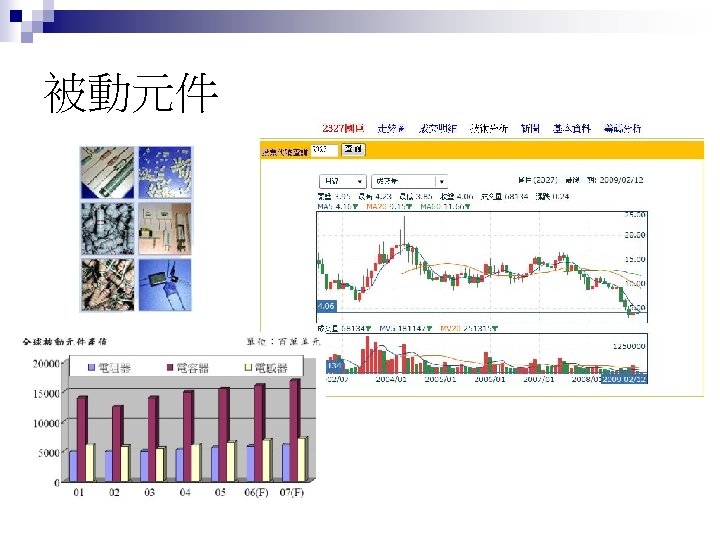被動元件

Resistors n n v(t) = Ri(t) or i(t)=Gv(t) R is the resistance G is called the conductance For linear time-invariant resistors, R and G are constants.

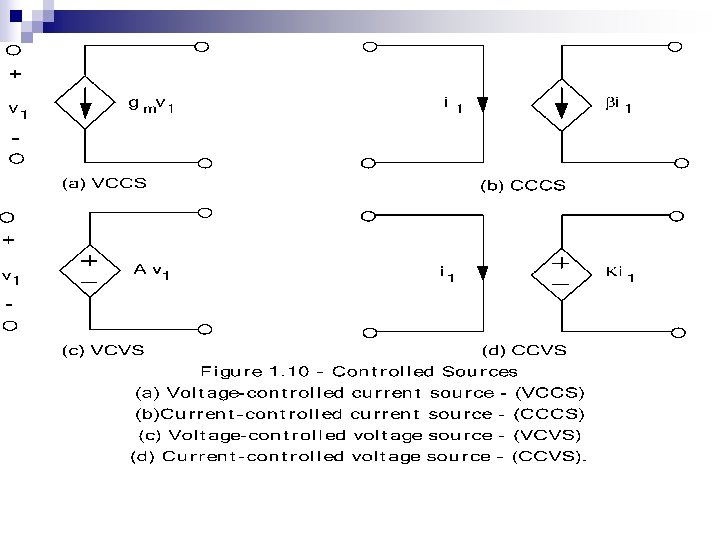
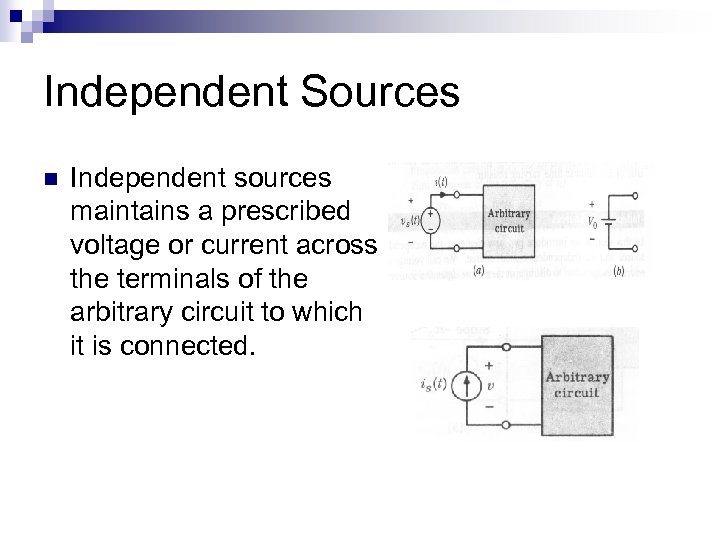Independent Sources n Independent sources maintains a prescribed voltage or current across the terminals of the arbitrary circuit to which it is connected.

Capacitors store electrical charges. n i(t) = dq/dt n q(t) = Cv(t) n i(t) = Cdv(t)/dt n

Parallel Plate Capacitance n n K = relative permittivity of the dielectric material in between two plates. K= 1 for free space, K=3. 9 for Si. O 2 High K (K > 3. 9)dielectric (e. g. (Ba. Sr)Ti. O 3, barium strontium titanate for K=160 -600 for storage capacitance; zirconium silicate, Zr. Si. O 4 with K=15 for next generation gate oxide) Low K (K < 3. 9)dielectric for ILD (interlayer dielectrics ) to insulate between metal lines (e. g. Porous Si. O 2 for K=1. 3)

Inductors store energy in their magnetic fields. n V(t) = dΦ/dt n Φ(t)=Li(t) n V(t) = L di/dt n

RLC Effects in Real Circuit Power (Thermal) n Time Delay n

Physical Componenets vs. Circuit Elements Range of Operation n Temperature Effect n Parasitic effect n Typical Element Size n ¨ Resistor : 1 ohm to Mohms ¨ Capacitor : femto Farad to micro Farad

Circuit Theory Review: Voltage Division and Applying KVL to the loop, and Combining these yields the basic voltage division formula:

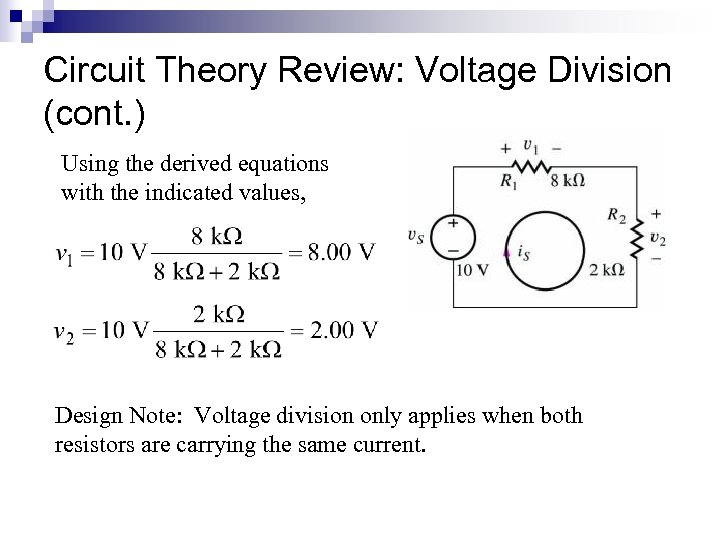Circuit Theory Review: Voltage Division (cont. ) Using the derived equations with the indicated values, Design Note: Voltage division only applies when both resistors are carrying the same current.

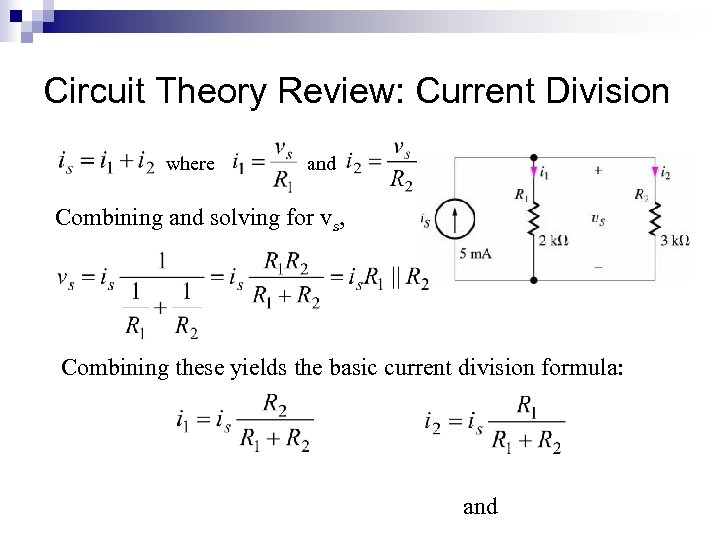Circuit Theory Review: Current Division where and Combining and solving for vs, Combining these yields the basic current division formula: and

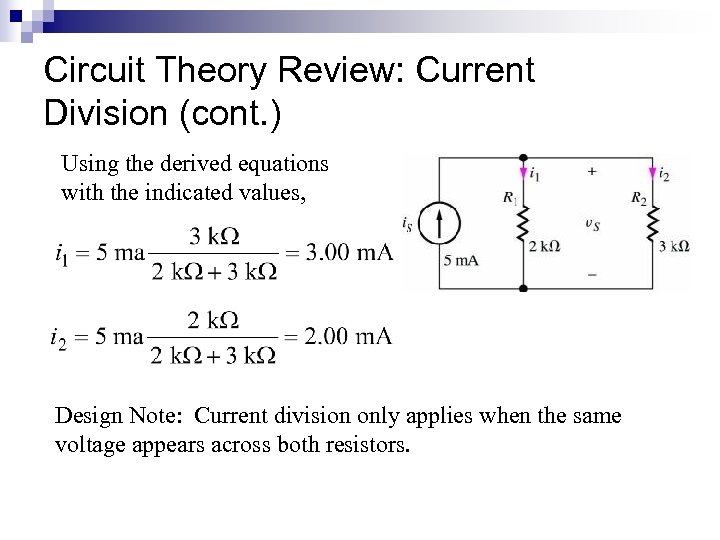Circuit Theory Review: Current Division (cont. ) Using the derived equations with the indicated values, Design Note: Current division only applies when the same voltage appears across both resistors.

Equivalent Circuit Thevenin and Norton Equivalent circuit represents real-world battery models. n Complex circuits can be simplified to these representation to help us understand the circuits. n

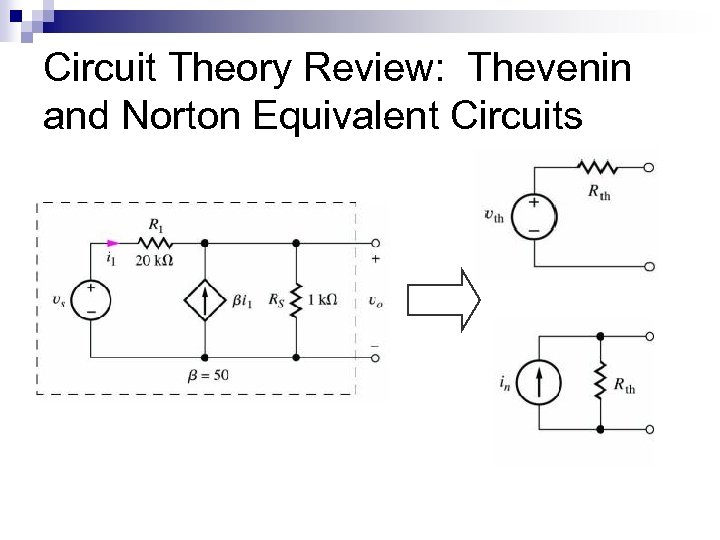Circuit Theory Review: Thevenin and Norton Equivalent Circuits

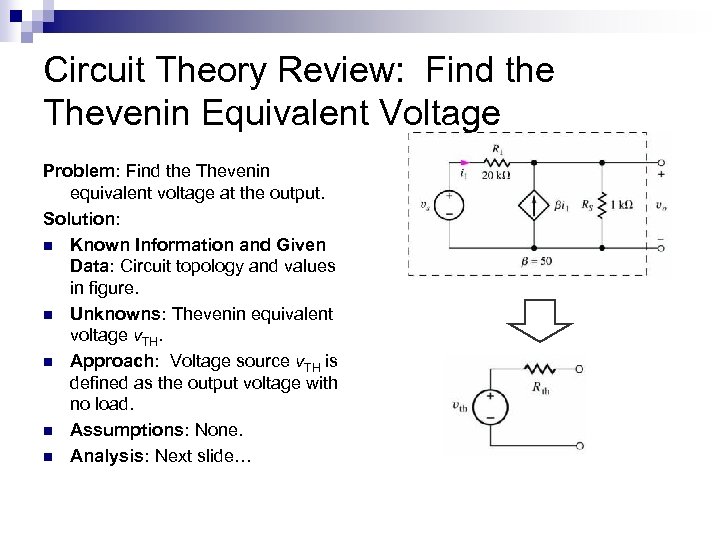Circuit Theory Review: Find the Thevenin Equivalent Voltage Problem: Find the Thevenin equivalent voltage at the output. Solution: n Known Information and Given Data: Circuit topology and values in figure. n Unknowns: Thevenin equivalent voltage v. TH. n Approach: Voltage source v. TH is defined as the output voltage with no load. n Assumptions: None. n Analysis: Next slide…

Circuit Theory Review: Find the Thevenin Equivalent Voltage Applying KCL at the output node, Current i 1 can be written as: Combining the previous equations

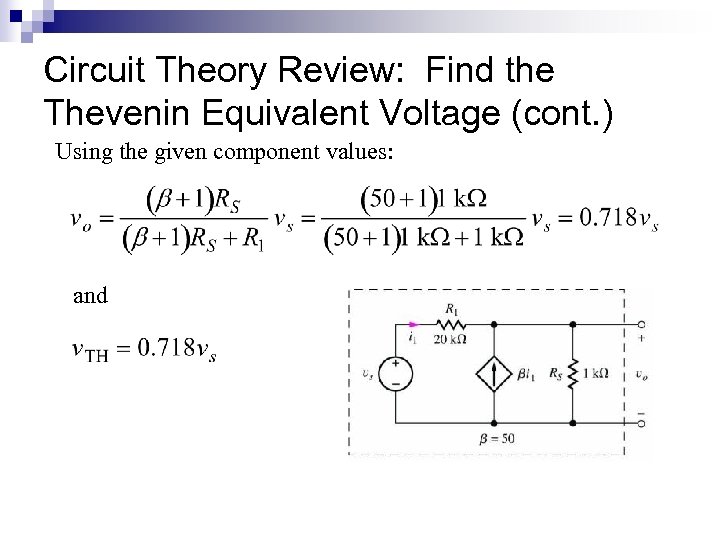Circuit Theory Review: Find the Thevenin Equivalent Voltage (cont. ) Using the given component values: and

Circuit Theory Review: Find the Thevenin Equivalent Resistance Problem: Find the Thevenin equivalent resistance. Solution: n Known Information and Given Data: Circuit topology and values in figure. n Unknowns: Thevenin equivalent resistance RTH. n Approach: RTH is defined as the equivalent resistance at the output terminals with all independent sources in the network set to zero. n Assumptions: None. n Analysis: Next slide… Test voltage vx has been added to the previous circuit. Applying vx and solving for ix allows us to find the Thevenin resistance as vx/ix.

Circuit Theory Review: Find the Thevenin Equivalent Resistance (cont. ) Applying KCL,

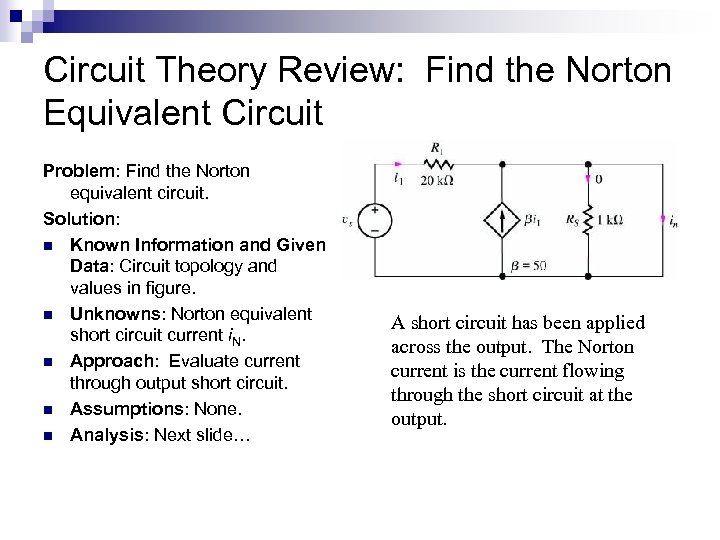Circuit Theory Review: Find the Norton Equivalent Circuit Problem: Find the Norton equivalent circuit. Solution: n Known Information and Given Data: Circuit topology and values in figure. n Unknowns: Norton equivalent short circuit current i. N. n Approach: Evaluate current through output short circuit. n Assumptions: None. n Analysis: Next slide… A short circuit has been applied across the output. The Norton current is the current flowing through the short circuit at the output.

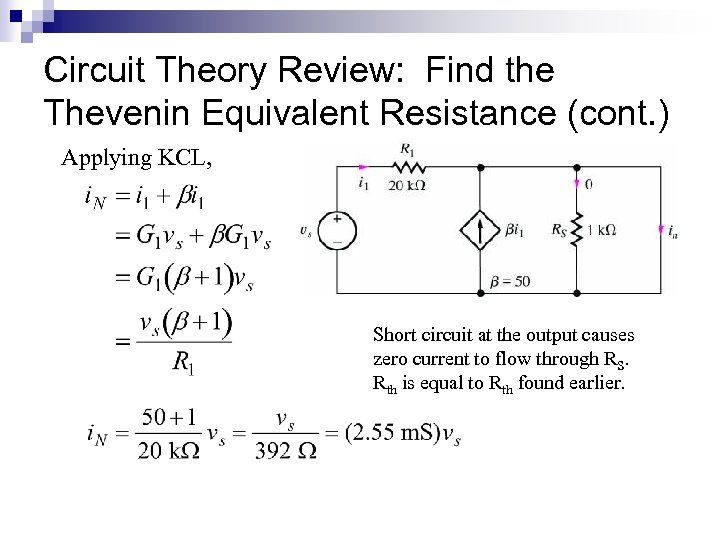Circuit Theory Review: Find the Thevenin Equivalent Resistance (cont. ) Applying KCL, Short circuit at the output causes zero current to flow through RS. Rth is equal to Rth found earlier.

Final Thevenin and Norton Circuits Check of Results: Note that v. TH=i. NRth and this can be used to check the calculations: i. NRth=(2. 55 m. S)vs(282 ) = 0. 719 vs, accurate within round-off error. While the two circuits are identical in terms of voltages and currents at the output terminals, there is one difference between the two circuits. With no load connected, the Norton circuit still dissipates power!

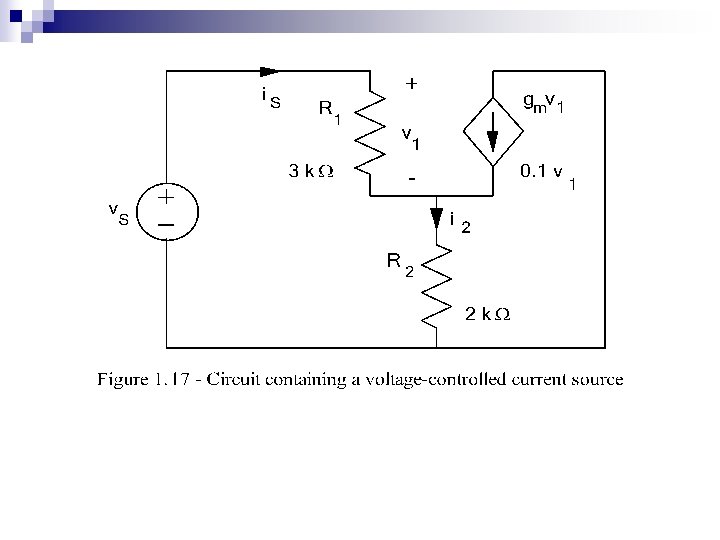
Example : Circuit with a controlled source n n n Applying KVL around the loop containing vs yields vs = is. R 1 + i 2 R 2 = is. R 1 + (is + gmv 1)R 2 (1. 33) v 1 = is. R 1 (1. 34) vs = is(R 1 + R 2 + gm. R 1 R 2) (1. 35) Req = vs / is = R 1 + R 2 (1+ gm. R 1) (1. 36) Req = 3 KΩ+2 KΩ[1+0. 1 S*3 KΩ] = 605 kΩ. This value is far larger than either R 1 or R 2.

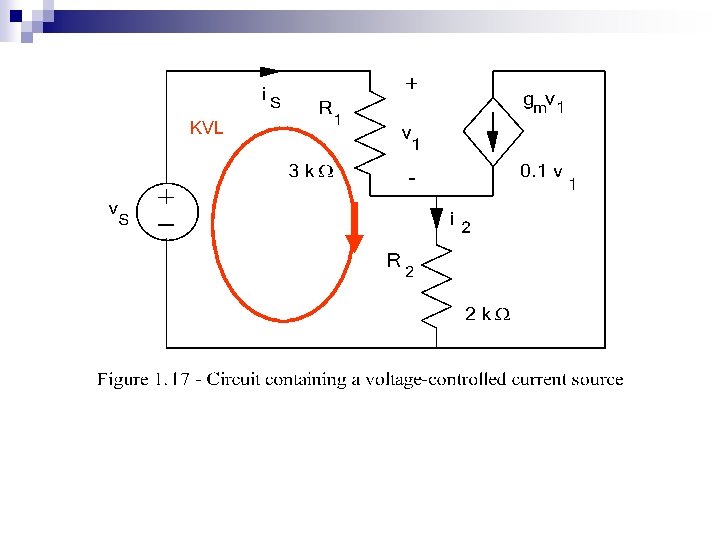KVL

Circuitry Snacks from : www. evilmadscientist. com

Joule Thief

555 LED Blink

Frequency Spectrum of Electronic Signals n n Nonrepetitive signals have continuous spectra often occupying a broad range of frequencies Fourier theory tells us that repetitive signals are composed of a set of sinusoidal signals with distinct amplitude, frequency, and phase. The set of sinusoidal signals is known as a Fourier series. The frequency spectrum of a signal is the amplitude and phase components of the signal versus frequency.

Frequencies of Some Common Signals n n n n Audible sounds Baseband TV FM Radio Television (Channels 2 -6) Television (Channels 7 -13) Maritime and Govt. Comm. Cell phones Satellite TV 20 Hz - 20 0 - 4. 5 88 - 108 54 - 88 174 - 216 - 450 1710 - 2690 3. 7 - 4. 2 KHz MHz MHz MHz GHz

Amplifier Basics n n n Analog signals are typically manipulated with linear amplifiers. Although signals may be comprised of several different components, linearity permits us to use the superposition principle. Superposition allows us to calculate the effect of each of the different components of a signal individually and then add the individual contributions to the output.

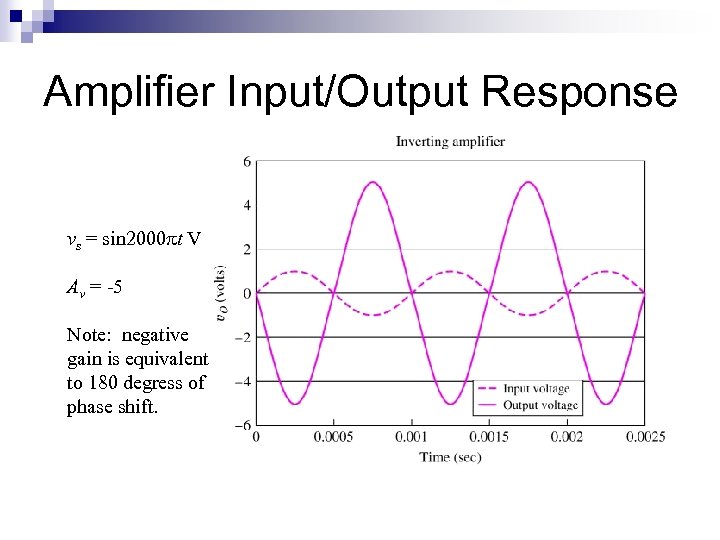Amplifier Input/Output Response vs = sin 2000 t V Av = -5 Note: negative gain is equivalent to 180 degress of phase shift.

Amplifier Frequency Response Amplifiers can be designed to selectively amplify specific ranges of frequencies. Such an amplifier is known as a filter. Several filter types are shown below: Low-Pass High-Pass Band-Reject All-Pass

Circuit Element Variations n All electronic components have manufacturing tolerances. Resistors can be purchased with 10%, 5%, and 1% tolerance. (IC resistors are often 10%. ) ¨ Capacitors can have asymmetrical tolerances such as +20%/-50%. ¨ Power supply voltages typically vary from 1% to 10%. ¨ n n n Device parameters will also vary with temperature and age. Circuits must be designed to accommodate these variations. We will use worst-case and Monte Carlo (statistical) analysis to examine the effects of component parameter variations.

Tolerance Modeling For symmetrical parameter variations PNOM(1 - ) P PNOM(1 + ) n For example, a 10 K resistor with 5% percent tolerance could take on the following range of values: 10 k(1 - 0. 05) R 10 k(1 + 0. 05) 9, 500 R 10, 500 n

Circuit Analysis with Tolerances n Worst-case analysis Parameters are manipulated to produce the worst-case min and max values of desired quantities. ¨ This can lead to over design since the worst-case combination of parameters is rare. ¨ It may be less expensive to discard a rare failure than to design for 100% yield. ¨ n Monte-Carlo analysis Parameters are randomly varied to generate a set of statistics for desired outputs. ¨ The design can be optimized so that failures due to parameter variation are less frequent than failures due to other mechanisms. ¨ In this way, the design difficulty is better managed than a worst-case approach. ¨

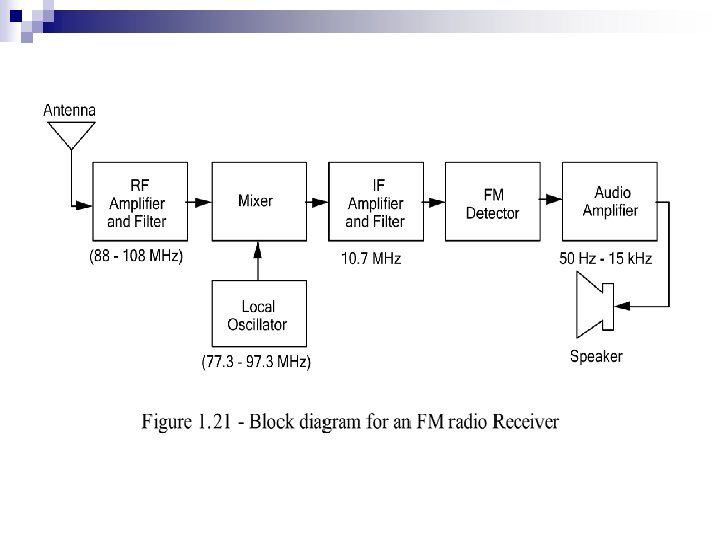
Amplifiers in a familiar electronic system The local oscillator, which tunes the radio receiver to select the desired station. n The mixer circuit actually changes the frequency of the incoming signal and is thus a nonlinear circuit. n

HW 1 1. 2 n 1. 11 n 1. 20 n 1. 22 n 1. 48 n