0e3d4b3f827cc13cb59f40c9a35572d4.ppt
- Количество слайдов: 70

Digital Design: Combinational Logic Principles Credits: Slides adapted from: J. F. Wakerly, Digital Design, 4/e, Prentice Hall, 2006 C. H. Roth, Fundamentals of Logic Design 5/e, Thomson, 2004 , A. B. Marcovitz, Intro. to Logic and Computer Design Mc. Graw Hill, 2008 , R. H. Katz, G. Borriello, Contemporary Logic Design 2/e, Prentice-Hall, 2005 , 1
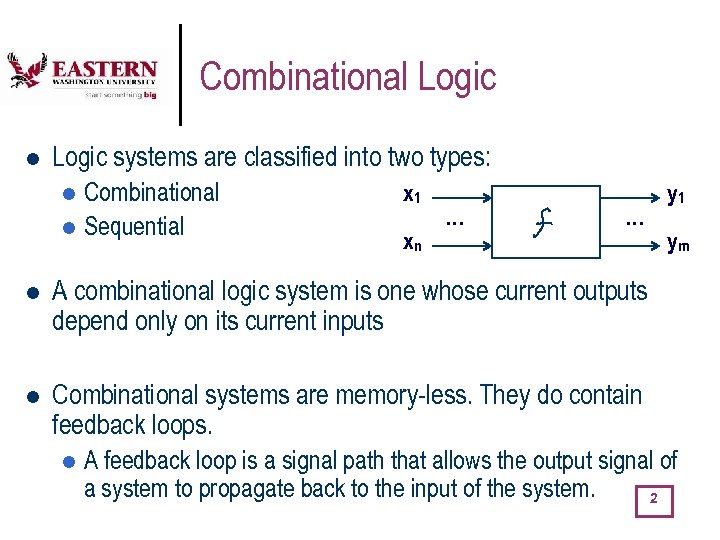
Combinational Logic systems are classified into two types: Combinational l Sequential l x 1 … … xn l ym A combinational logic system is one whose current outputs depend only on its current inputs l y 1 Combinational systems are memory-less. They do contain feedback loops. l A feedback loop is a signal path that allows the output signal of a system to propagate back to the input of the system. 2

Analysis and Design of combinational logic systems l Goal: analysis and design of logic functions whose current outputs depends only on their current inputs l Represent each of the inputs and outputs as binary patterns Formalize the function specification of the system in the form of a table or an algebraic expression l 3

Switching Algebra l Switching algebra is binary l l that is all variables and constants take on one of two values: {0, 1} Switching algebra is based on three elementary operations: l NOT, AND, OR 4
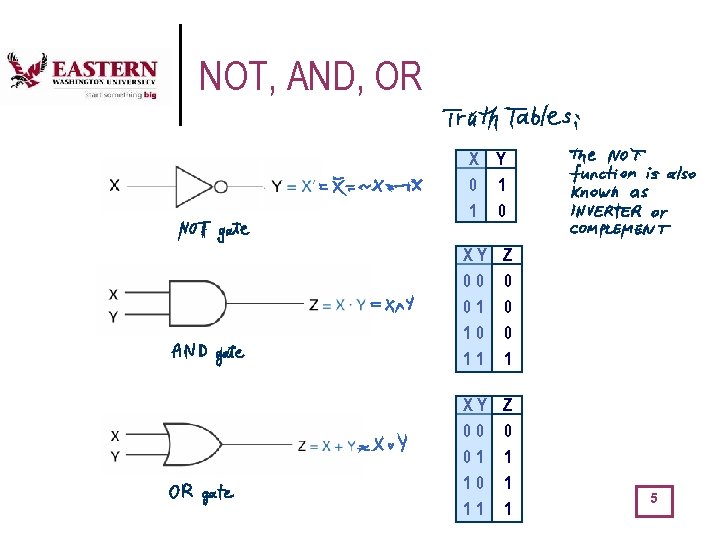
NOT, AND, OR X Y 0 1 1 0 XY 00 01 10 11 Z 0 0 0 1 XY 00 01 10 11 Z 0 1 1 1 5

NOT, AND, OR as switches X 0 Y=X’ 1 X 1 1 Y Z = X Y X Z = X + Y 6 Y

Switching Algebra Axioms l Axioms (= postulates) of a mathematical system: minimal set of basic definitions from which all other information can be derived 7

Principle of Duality Because of the duality of axioms any theorem in switching algebra remains true as far as 0 and 1 are swapped and + are swapped. 8

Useful Properties of Switching Algebra Operations with 0 and 1: 1. X + 0 = X 1 D. X • 1 = X 2. X + 1 = 1 2 D. X • 0 = 0 Idempotent Theorem: 3. X + X = X 3 D. X • X = X Involution Theorem: 4. (X' )' = X Theorem of Complementarity: 5. X + X' = 1 5 D. X • X' = 0 9

Useful Properties of Switching Algebra Commutative law: 6. X + Y = Y + X 6 D. X • Y = Y • X Associative law: 7. (X + Y) + Z = X + (Y + Z) = X + Y + Z 7 D. (X Y)Z = X(Y Z) = X Y Z Distributive law: 8. X(Y + Z) = XY + XZ 8 D. X + YZ = (X + Y)(X + Z) Simplification theorems: 9. XY + XY' = X 9 D. (X + Y)(X + Y' ) = X 10. X + XY = X 10 D. X(X + Y) = X 11. (X + Y' )Y = XY 11 D. XY' + Y = X + Y 10

Useful Properties of Switching Algebra De. Morgan's laws: 12. (X + Y + Z +. . . )' = X'Y'Z'. . . 12 D. (XYZ. . . )' = X' + Y' + Z' +. . . Shannon’s Expansion Theorem: 13. F(X, Y, Z, . . . ) = X • F(1, Y, Z, . . . ) + X' • F(0, Y, Z, . . . ) 13 D. F(X, Y, Z, . . . ) = [X + F(0, Y, Z, . . . ) ] • [X' + F(1, Y, Z, . . . )] Theorem for multiplying out and factoring: 14. (X + Y)(X' + Z) = XZ + X'Y 14 D. XY + X'Z = (X+Z)(X'+Y) Consensus theorem (muxing): 15. XY + YZ + X'Z = X Y + X'Z 11 15 D. (X+Y)(Y+Z)(X'+Z) = (X+Y)(X'+Z)
Representations of Logic Functions l Truth Tables Table that shows the output value for each combination of the inputs. The truth table for an n-variable (n-inputs) logic function has 2 n rows. Algebraic expressions l Karnaugh Maps l 12

Common Terminology l l l Literal The appearance of a variable or its complement Product Term One or more literals connected by AND operators Sum Term One or more literals connected by OR operators 13

Common Terminology (cont’d) l l l Sum of Products (SOP) One or more product terms connected by OR operator Product of Sums (POS) One or more sum terms connected by AND operator Standard (=Normal) Product Term also called minterm A product term that includes each variable of the problem either uncomplemented or complemented 14

Common Terminology (cont’d) l l l Canonical Sum (of products) Is a sum of minterms Standard (= Normal) Sum Term also calledmaxterm A sum term that include each variable of the problem, either uncomplemented or complemented Canonical Product (of sums) Is a product of maxterms 15

Truth tables, minterms, and maxterms l l l There is a close correspondence between the truth table and minterms and maxterms A minterm is a product term that is 1 in exactly one row of the truth table Similarly (by duality) a maxterm is a sum term that is 0 in exactly one row of the truth table An n-variable minterm can be represented by an n-bit integer. Thus, we we can use mi to denote the minterm corresponding row i of the truth table. For maxterm i (Mi), if the bit in the binary representation of i is 1, the corresponding variable is complemented 16
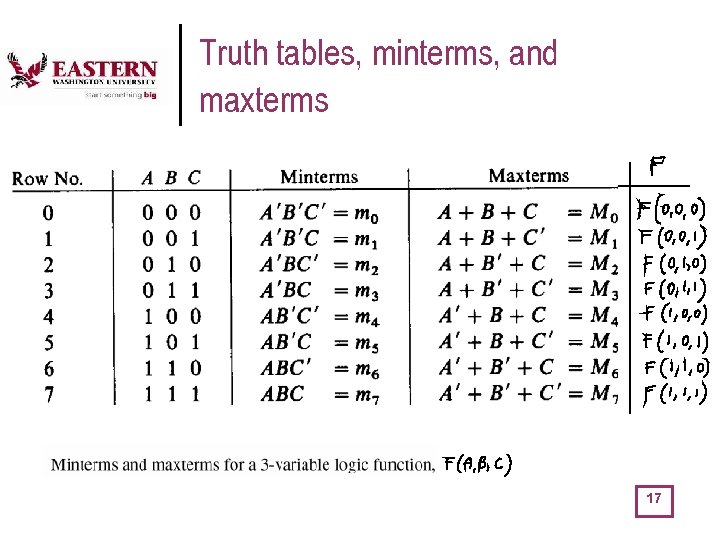
Truth tables, minterms, and maxterms 17

EXAMPLE 18

EXAMPLE 19

EXAMPLE 20

EXAMPLE … Lessons Learned … l l What is the best way (minimum) to express a logic function ? When can I stop with the algebraic manipulations ? 21

Logic functions representations So far, we have seen 3 ways for representing a logic function: l l Truth Table Canonical SOP • as algebraic sum of minterms or • as list of minterms using the notation Canonical POS • as algebraic product of maxterms or • as list of maxterms using the P notation … and soon we will see one more called K-maps 22

But, the issue is still there … how can we minimize logic functions ? l l The minimum logic expression for a function is the one with the fewest number of terms. If there are more than one expression with the same number of terms, the minimum is the one fewest number of literals. Since ultimately the goal of digital design is to come out with a circuit that implements the given logic function, let’s see what does minimization mean from a circuit perspective 23
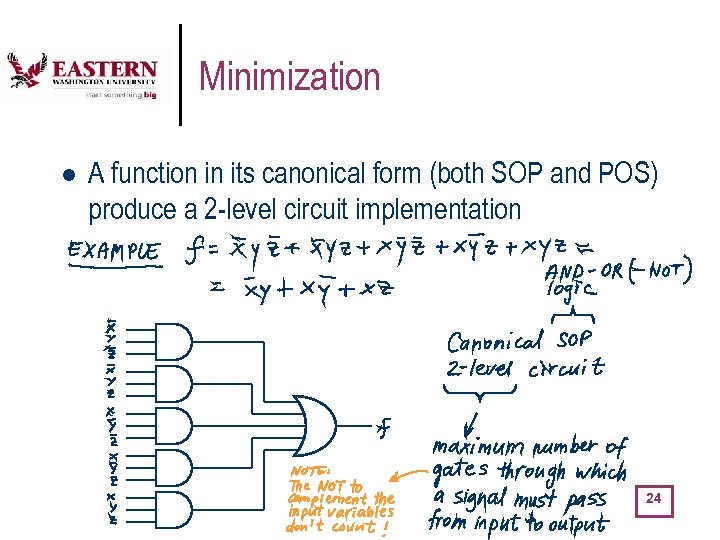
Minimization l A function in its canonical form (both SOP and POS) produce a 2 -level circuit implementation 24
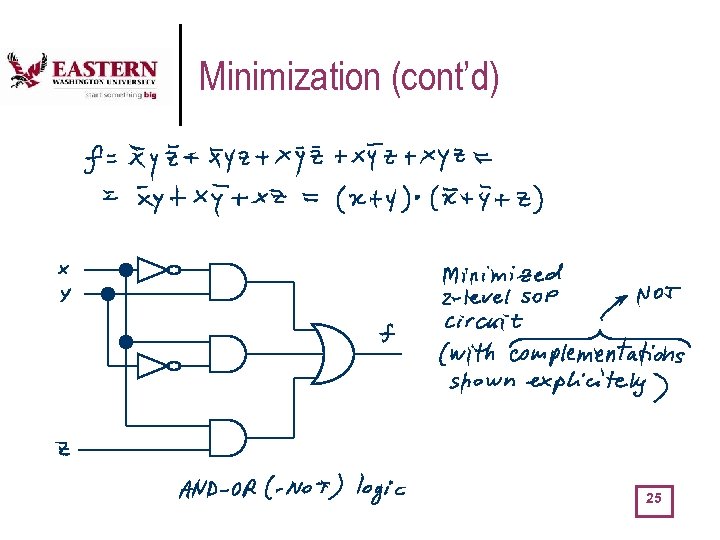
Minimization (cont’d) 25
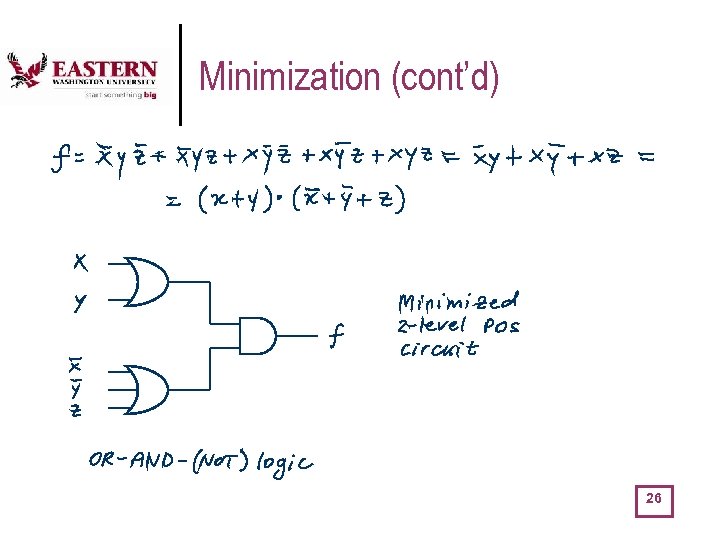
Minimization (cont’d) 26

Minimization (cont’d) l Minimization methods reduce the cost of a 2 -level circuit in two ways: l Minimizing the number of first-level gates • As a side effect the number of inputs on the second level gates results also minimized l Minimizing the number of inputs on each first level gate 27

Minimization (cont’d) l l Key tool to simplification is the uniting theorem: A (B’ + B) = A Essence of simplification of two-level logic l find two element subsets of the ON-set where only one variable changes its value – this single varying variable can be eliminated and a single product term used to represent both elements F = A’B’+AB’ = (A’+A)B’ = B’ A B F 0 0 1 0 1 1 1 0 B has the same value in both on-set rows B remains A has a different value in the two rows A is eliminated 28
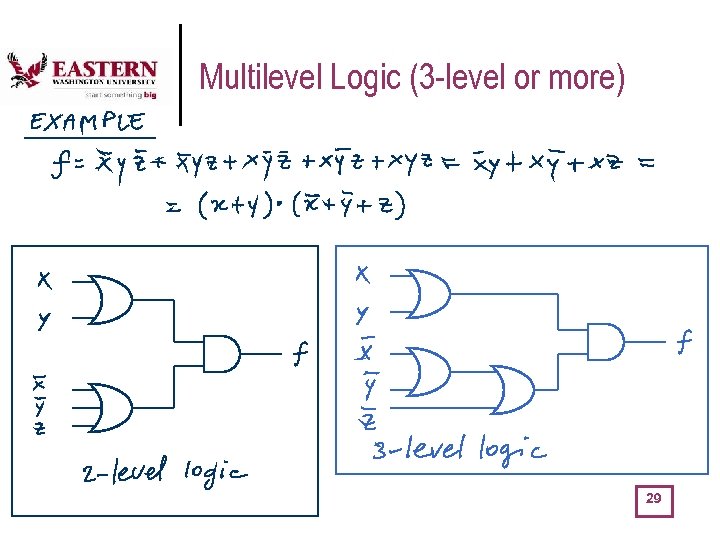
Multilevel Logic (3 -level or more) 29
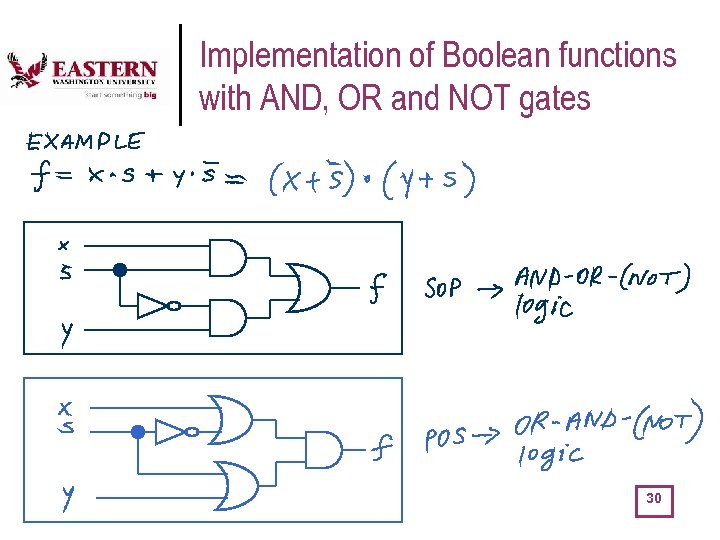
Implementation of Boolean functions with AND, OR and NOT gates 30
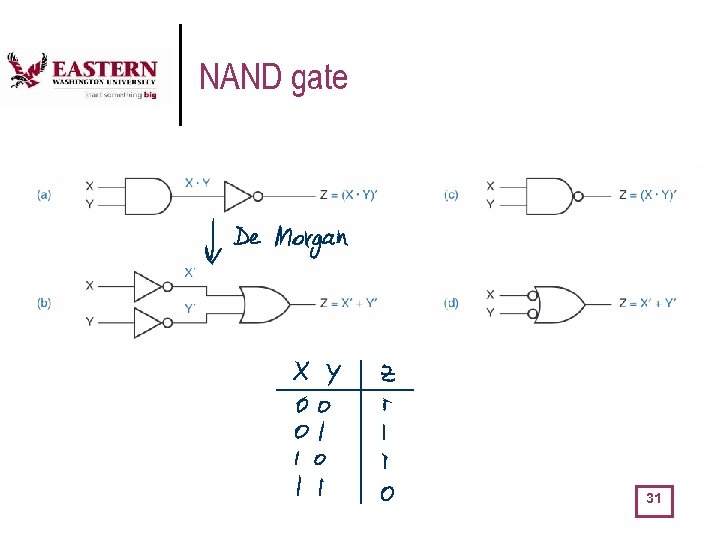
NAND gate 31
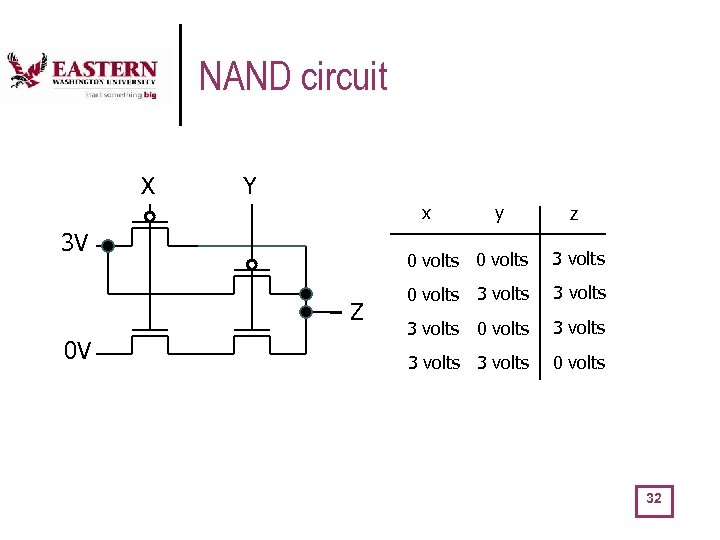
NAND circuit X Y x 3 V z 0 volts Z 0 V y 3 volts 0 volts 3 volts 3 volts 0 volts 32
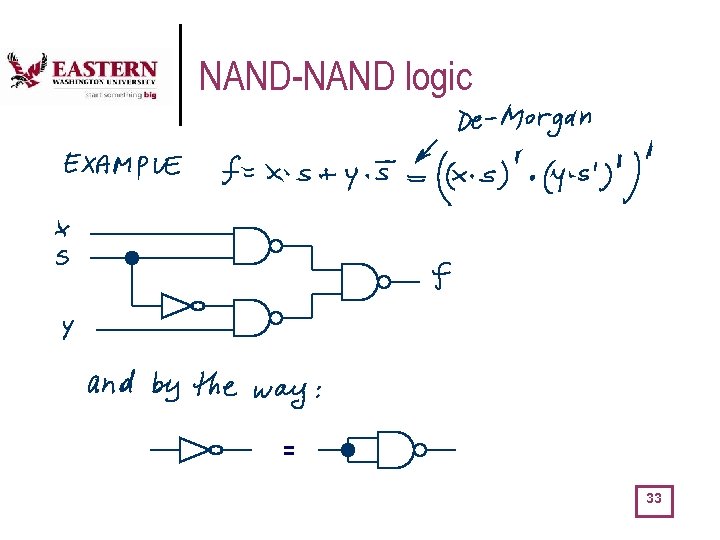
NAND-NAND logic = 33
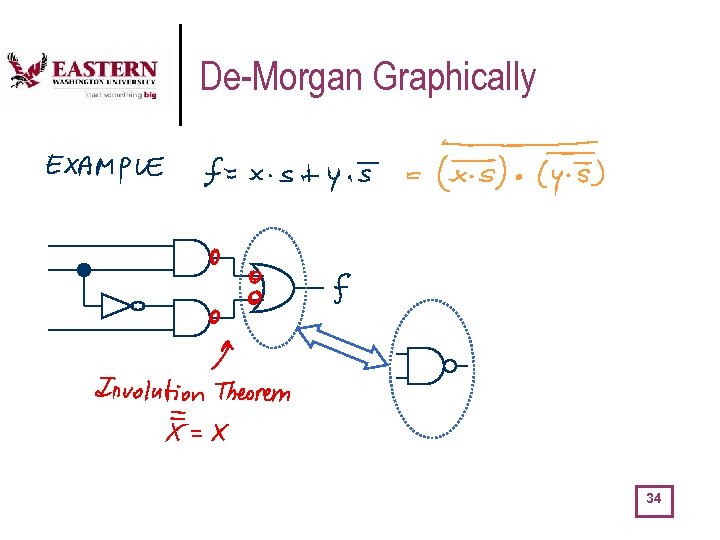
De-Morgan Graphically 34
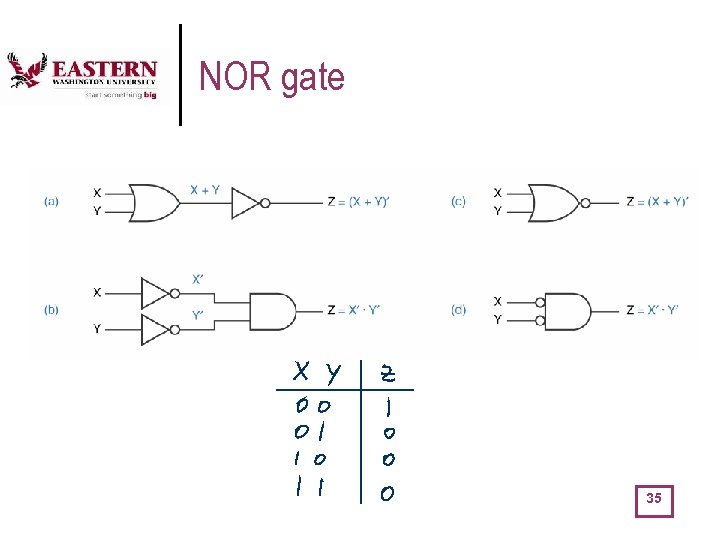
NOR gate 35
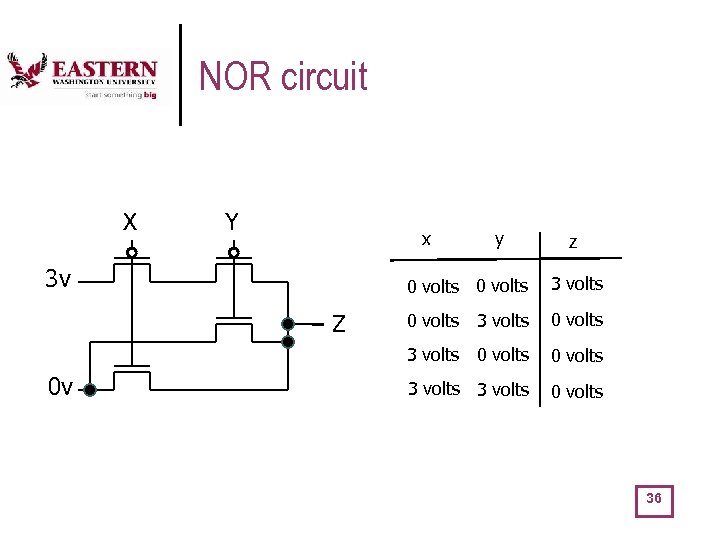
NOR circuit X Y x 3 v y z 0 volts 0 v 0 volts 3 volts 0 volts Z 3 volts 0 volts 36
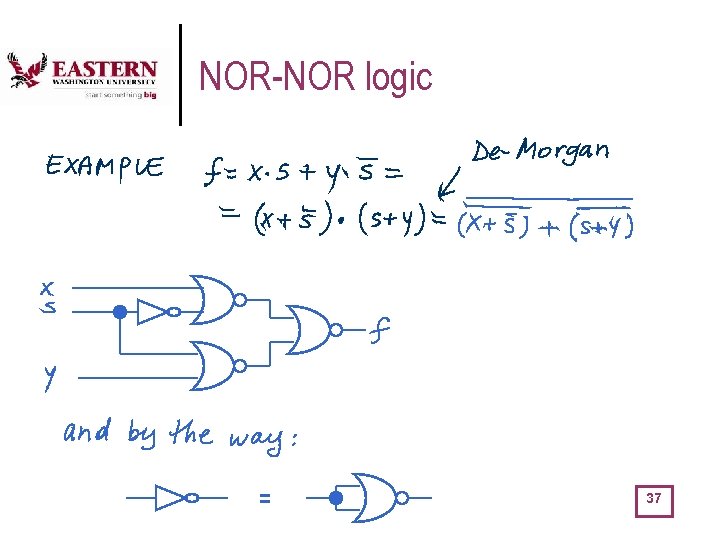
NOR-NOR logic = 37
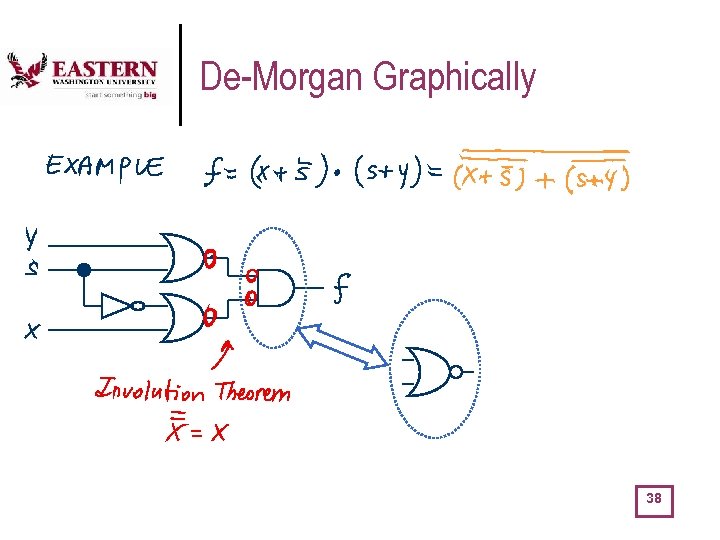
De-Morgan Graphically 38

Summarizing … OR is the same as NAND with complemented inputs l AND is the same as NOR with complemented inputs l NAND is the same as OR with complemented inputs l NOR is the same as AND with complemented inputs l 39

XOR and XNOR gates l XOR X Y Z X 0 0 1 1 Y 0 1 Z 0 1 1 0 X Y = X’ Y + X Y’ X Y expresses "inequality", "difference" (X Y) l XNOR X Y Z X 0 0 1 1 Y 0 1 Z 1 0 0 1 X Y = X Y + X’ Y’ X xnor Y expresses "equality", "coincidence" (X Y) 40

Exclusive OR Properties l l l l X 0 = X X 1 = X’ X X = X X X’= 0 X Y = Y X (commutative law) (X Y) Z = X (Y Z) =X Y Z (associative law) X(Y Z) = XY XZ (distributive law) (X Y)’ = X Y’ = X’ Y = XY + X’Y’ 41
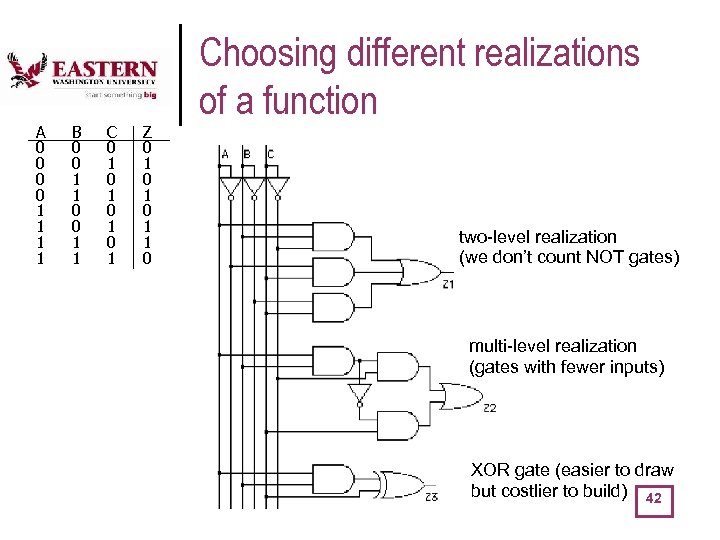
A 0 0 1 1 B 0 0 1 1 C 0 1 0 1 Z 0 1 0 1 1 0 Choosing different realizations of a function two-level realization (we don’t count NOT gates) multi-level realization (gates with fewer inputs) XOR gate (easier to draw but costlier to build) 42

Which realization is best? l l Reduce number of inputs l literal: input variable (complemented or not) • can approximate cost of logic gate as 2 transistors per literal • why not count inverters? l fewer literals means smaller gates • smaller gates means less transistors l fewer inputs implies faster gates • gates are smaller and thus also faster l fan-ins (# of gate inputs) are limited in some technologies Reduce number of gates l fewer gates (and the packages they come in) means smaller circuits 43 • directly influences manufacturing costs

Which realization is best? (cont’d) l Reduce number of levels of gates l l fewer level of gates implies reduced signal propagation delays How do we explore tradeoffs between increased circuit delay and size? automated tools to generate different solutions l logic minimization: reduce number of gates and complexity l logic optimization: reduction while trading off against delay l 44
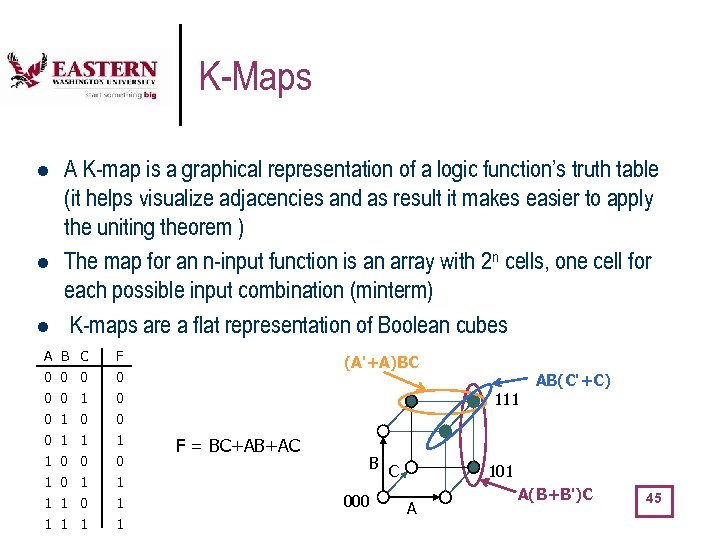
K-Maps l l l A K-map is a graphical representation of a logic function’s truth table (it helps visualize adjacencies and as result it makes easier to apply the uniting theorem ) The map for an n-input function is an array with 2 n cells, one cell for each possible input combination (minterm) K-maps are a flat representation of Boolean cubes A B C F 0 0 0 1 0 1 1 1 1 0 0 0 1 1 1 0 1 0 1 (A'+A)BC AB(C'+C) 111 F = BC+AB+AC B C 000 101 A A(B+B')C 45
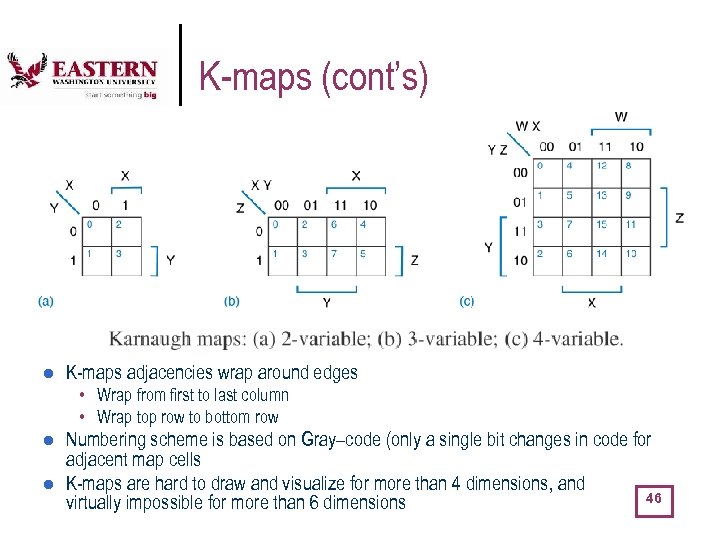
K-maps (cont’s) l K-maps adjacencies wrap around edges • Wrap from first to last column • Wrap top row to bottom row l l Numbering scheme is based on Gray–code (only a single bit changes in code for adjacent map cells K-maps are hard to draw and visualize for more than 4 dimensions, and 46 virtually impossible for more than 6 dimensions

K-maps (cont’d) TOOL: Apply over and over uniting theorem: a. XY + XY’ = X a-d. (X + Y)(X+Y’) = X RULE: find the smallest number of the largest possible subcubes (2 i adjacent cells) to cover the ON-set (fewer terms with fewer inputs per term) 47
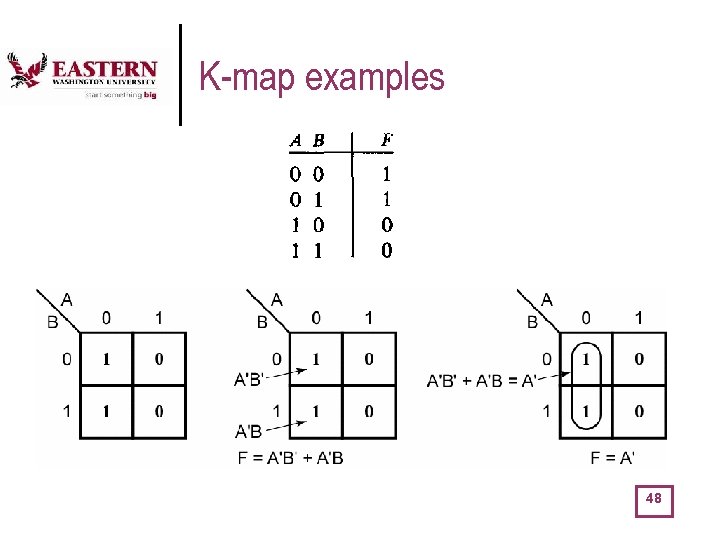
K-map examples 48
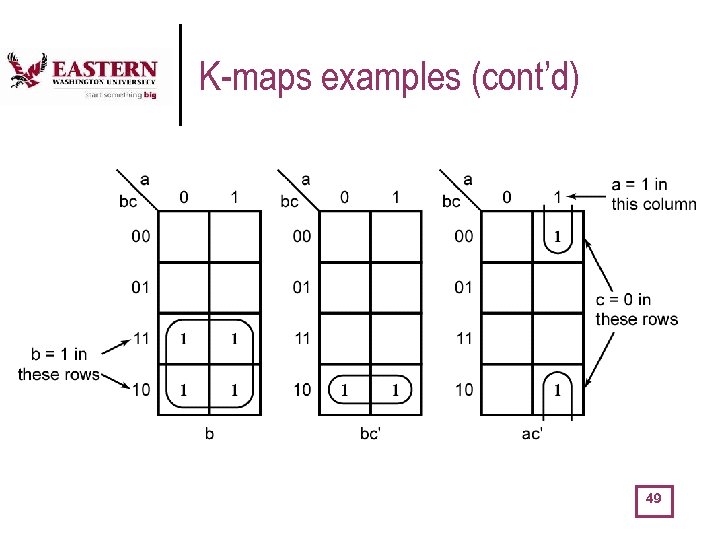
K-maps examples (cont’d) 49
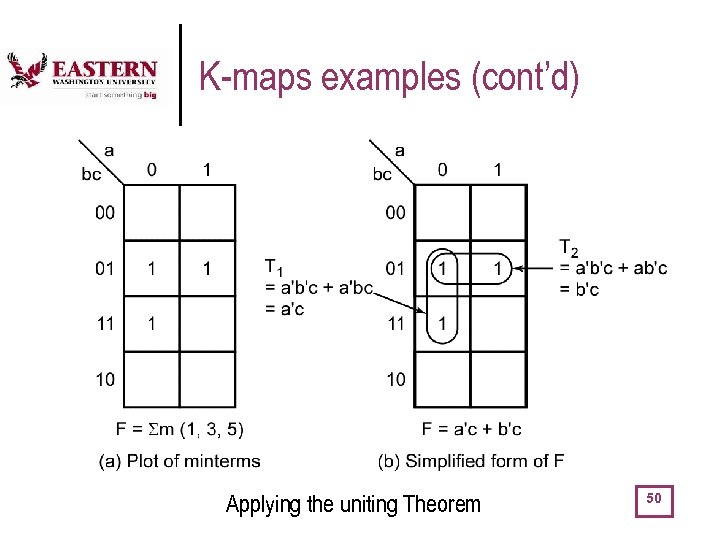
K-maps examples (cont’d) Applying the uniting Theorem 50
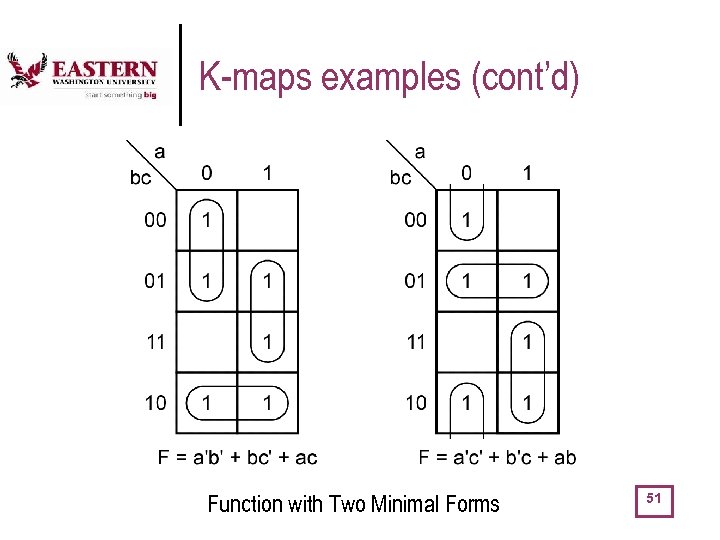
K-maps examples (cont’d) Function with Two Minimal Forms 51
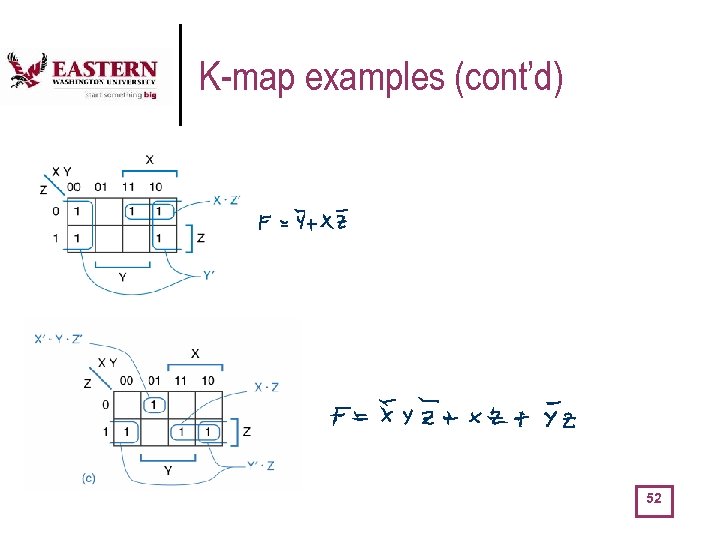
K-map examples (cont’d) 52
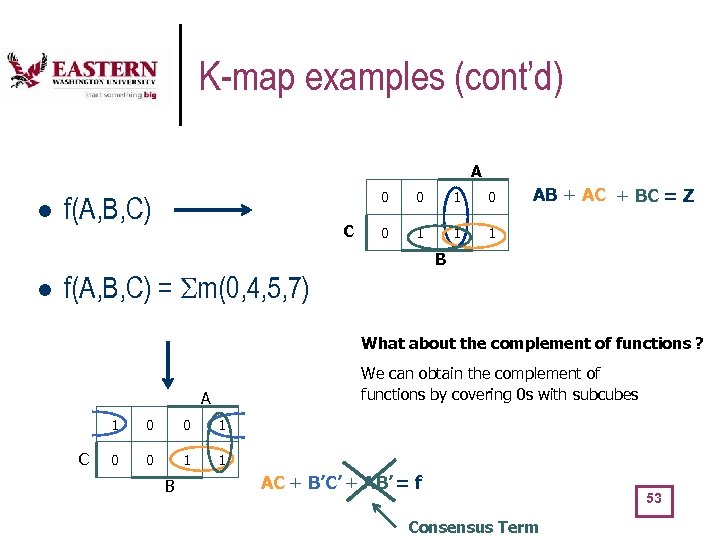
K-map examples (cont’d) A l 0 f(A, B, C) C 0 1 0 0 1 1 AB + AC + BC = Z 1 B l f(A, B, C) = m(0, 4, 5, 7) What about the complement of functions ? We can obtain the complement of functions by covering 0 s with subcubes A 1 C 0 0 1 1 B AC + B’C’ + AB’ = f Consensus Term 53
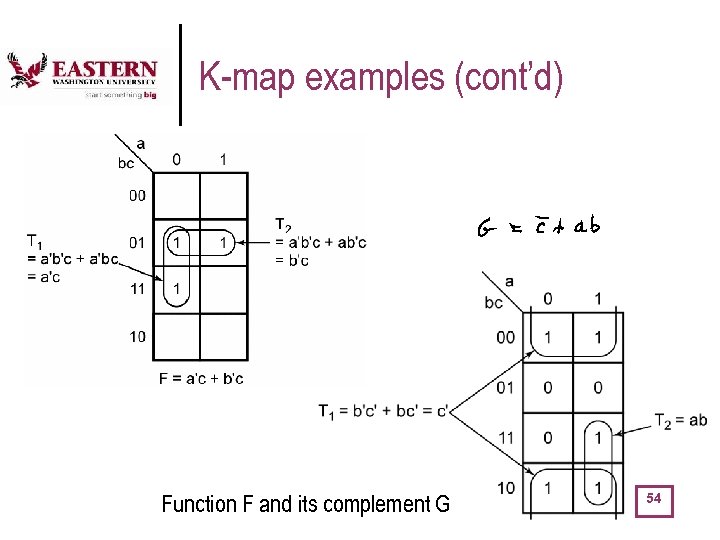
K-map examples (cont’d) Function F and its complement G 54
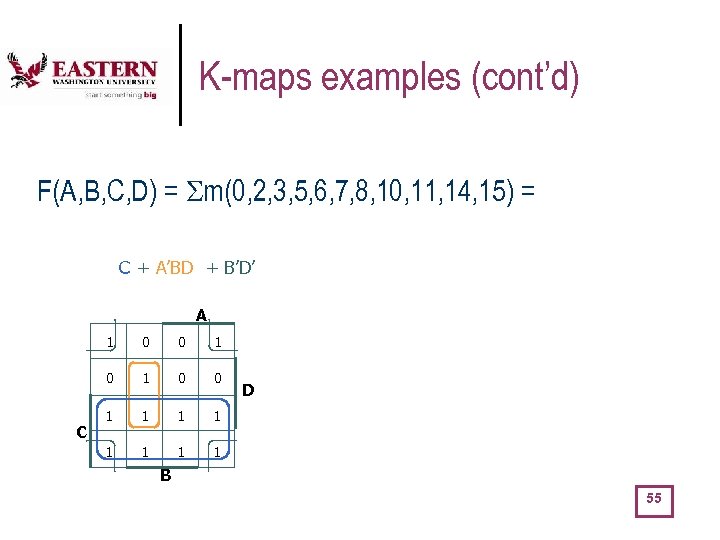
K-maps examples (cont’d) F(A, B, C, D) = m(0, 2, 3, 5, 6, 7, 8, 10, 11, 14, 15) = C + A’BD + B’D’ A 1 0 C 0 1 0 0 1 1 1 1 D B 55
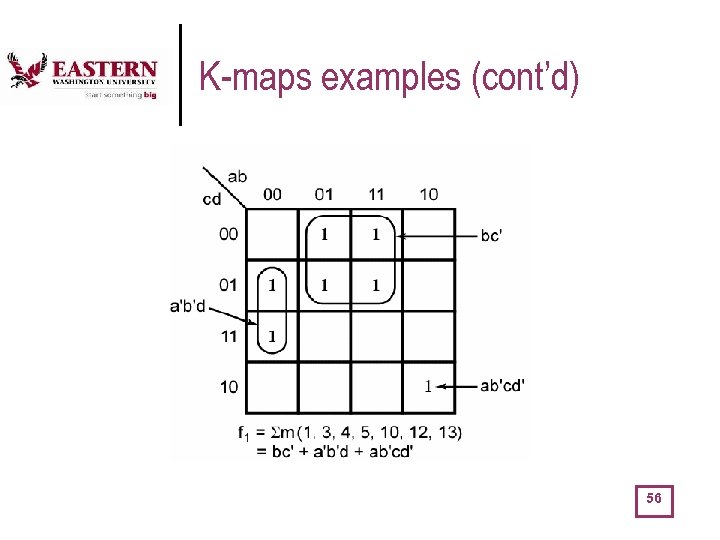
K-maps examples (cont’d) 56
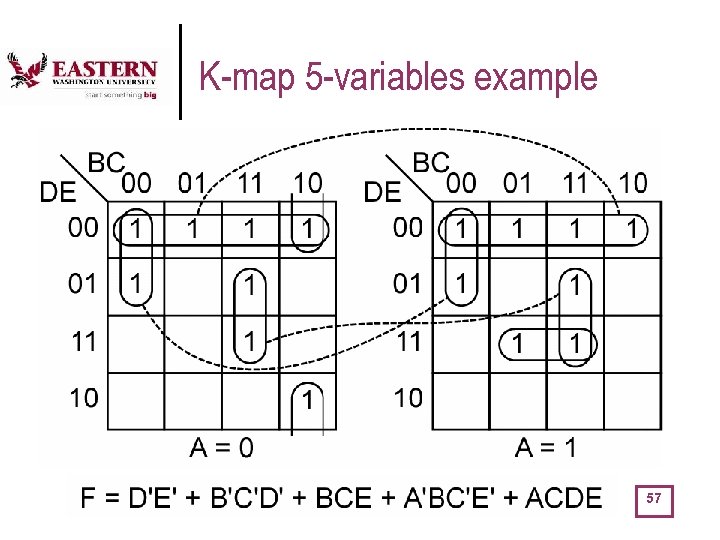
K-map 5 -variables example 57

Incompletely specified functions (don’t cares) l Sometime, not all input combinations are specified l f(A, B, C, D) = m(1, 3, 5, 7, 9) + d(6, 12, 13) l f= without don’t cares A’D + B’C’D A 0 - 0 1 C 0 1 - 1 1 1 0 0 0 - 0 0 B D 58

Karnaugh maps: don’t cares (cont’d) l f(A, B, C, D) = m(1, 3, 5, 7, 9) + d(6, 12, 13) f = A'D + B'C'D l f = A'D + C'D without don't cares with don't cares l A 0 - 0 1 C 0 1 - 1 1 1 0 0 0 - 0 0 B D by using don't care as a "1" a 2 -cube can be formed rather than a 1 -cube to cover this node don't cares can be treated as 1 s or 0 s depending on which is more advantageous 59
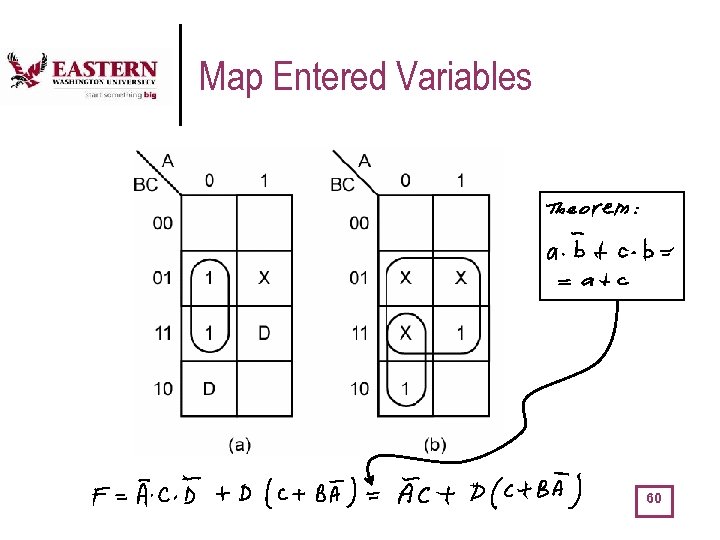
Map Entered Variables 60
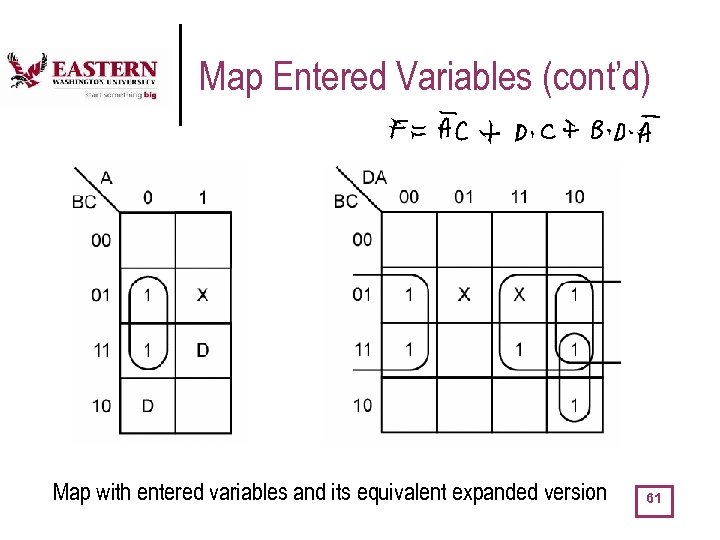
Map Entered Variables (cont’d) Map with entered variables and its equivalent expanded version 61
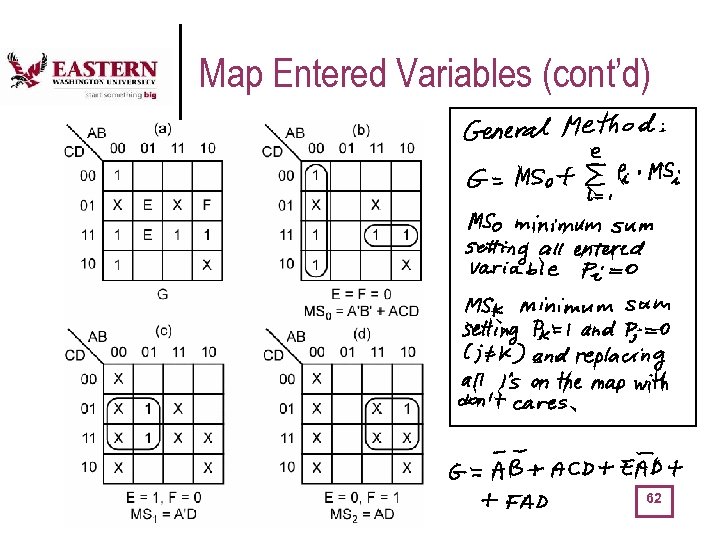
Map Entered Variables (cont’d) 62

More Terminology … l l l Implicant of a function F a single 1 (= minterm) or any group of 1’s which can be combined together in a K-map (i. e. , 1’s that are adjacent and which are grouped in a number that is always a power of 2). represents a product term which is called an implicant of a function F. An implicant represents a product term that can be used in a SOP expression for that function, that is, the function is 1 whenever the implicant is 1 (and maybe other times, as well …) Prime Implicant is an implicant that cannot be combined with another one to eliminate a literal. In other word each prime implicant corresponds to a product term in one of the minimum SOP expression for the function. A prime implicant is an implicant that is not fully contained in any other implicant. Essential prime implicant is a prime implicant that includes at least one 1 that is not included in any other prime implicant. In other words if a particular element of the on-set is covered by only one prime implicant, than that implicant is called an essential prime implicant. 63
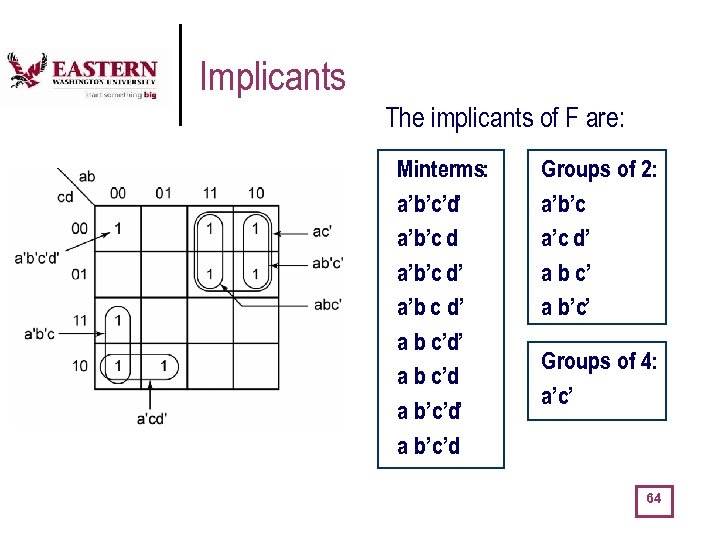
Implicants The implicants of F are: Minterms: a’b’c’d’ a’b’c d’ a’b c d’ a b c’d a b’c’d’ a b’c’d Groups of 2: a’b’c a’c d’ a b c’ a b’c’ Groups of 4: a’c’ 64
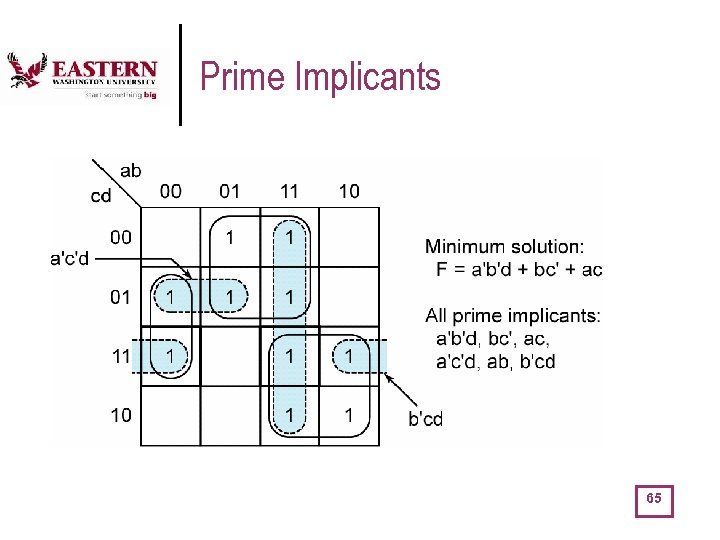
Prime Implicants 65
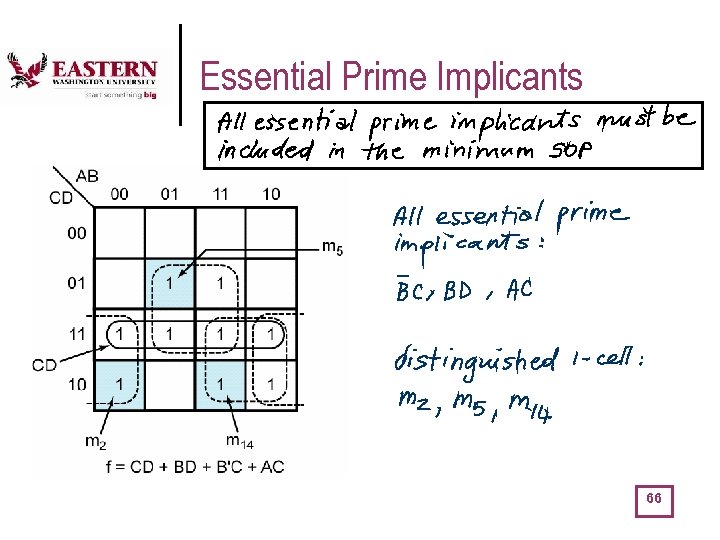
Essential Prime Implicants 66

Essential Prime Implicants (cont’d) 67
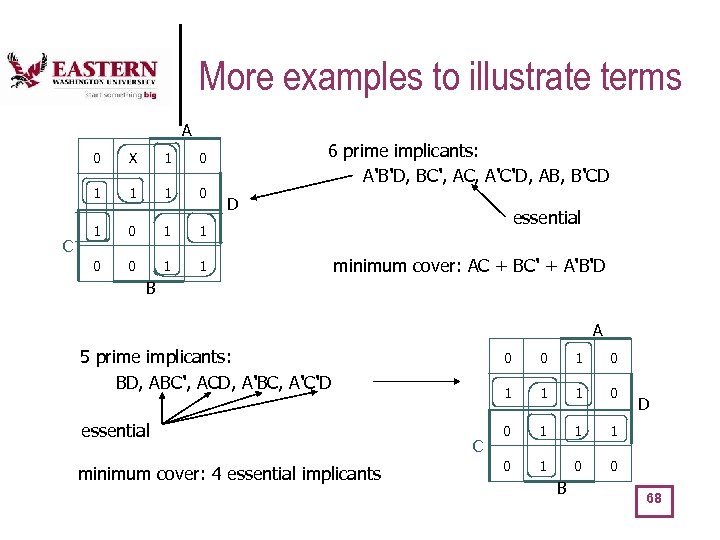
More examples to illustrate terms A 0 1 1 1 0 0 1 6 prime implicants: A'B'D, BC', AC, A'C'D, AB, B'CD 0 1 C X 1 D essential minimum cover: AC + BC' + A'B'D B A 5 prime implicants: BD, ABC', ACD, A'BC, A'C'D essential minimum cover: 4 essential implicants 0 1 C 0 1 1 0 0 1 1 1 0 0 B D 68
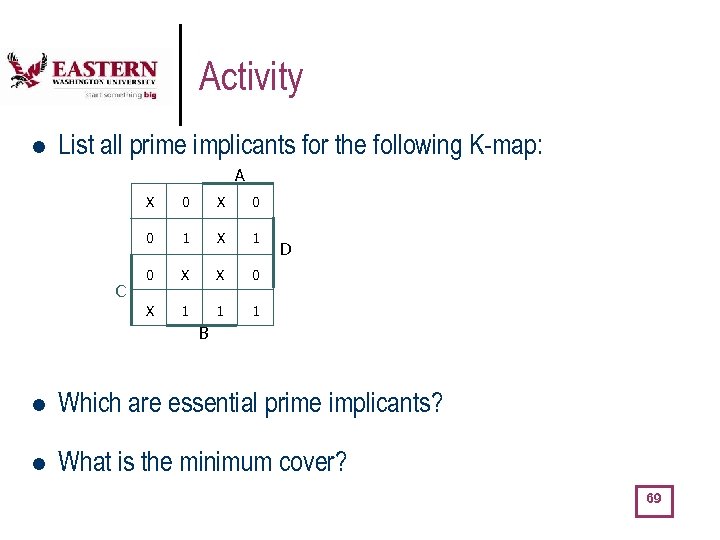
Activity l List all prime implicants for the following K-map: A X X 0 0 1 X 1 0 X X 0 X C 0 1 1 1 D CD’ BC BD AB AC’D B l Which are essential prime implicants? CD’ BD AC’D l What is the minimum cover? CD’ BD AC’D 69
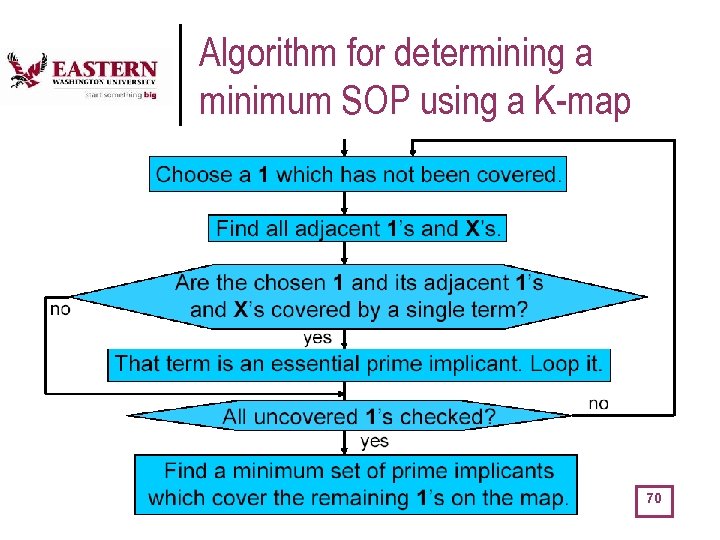
Algorithm for determining a minimum SOP using a K-map 70
0e3d4b3f827cc13cb59f40c9a35572d4.ppt