Digital Design: An Embedded Systems Approach Using Verilog Chapter 2 Combinational Basics Portions of this work are from the book, Digital Design: An Embedded Systems Approach Using Verilog, by Peter J. Ashenden, published by Morgan Kaufmann Chapter — Combinational Basics Digital Design — Publishers, 2 Copyright 2007 Elsevier Inc. All rights reserved.
Verilog Combinational Circuits n Circuits whose outputs depend only on current input values n no storage of past input values no state Can be analyzed using laws of logic n Boolean algebra, similar to propositional calculus Digital Design — Chapter 2 — Combinational Basics 2
Verilog Boolean Functions operating on two-valued inputs giving two-valued outputs n n n 0, implemented as a low voltage level 1, implemented as a high voltage level Function defines output value for all possible combinations of input value Digital Design — Chapter 2 — Combinational Basics 3
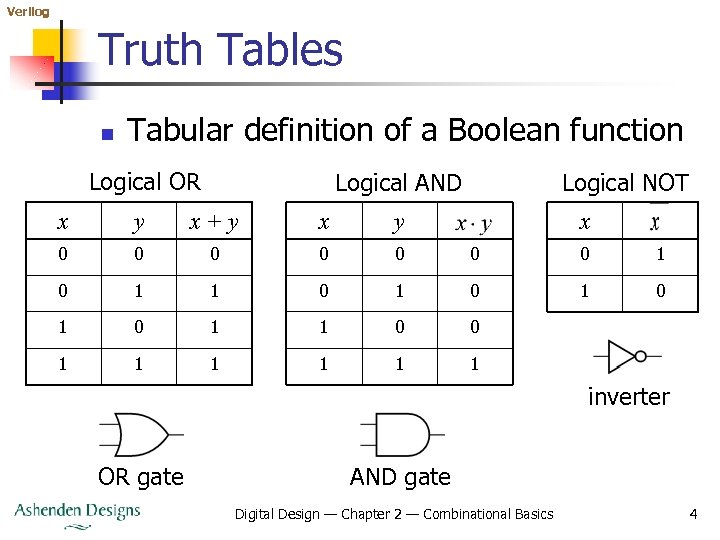
Verilog Truth Tables n Tabular definition of a Boolean function Logical OR Logical AND Logical NOT x y x+y x 0 0 0 0 1 1 0 1 0 1 1 0 0 1 1 1 inverter OR gate AND gate Digital Design — Chapter 2 — Combinational Basics 4
Verilog Boolean Expressions n n n Combination of variables, 0 and 1 literals, operators: Parentheses for order of evaluation Precedence: · before + Digital Design — Chapter 2 — Combinational Basics 5
Verilog Boolean Equations n Equality relation between Boolean expressions n n n Often, LHS is a single variable name The Boolean equation then defines a function of that name Implemented as a combinational circuit Digital Design — Chapter 2 — Combinational Basics 6
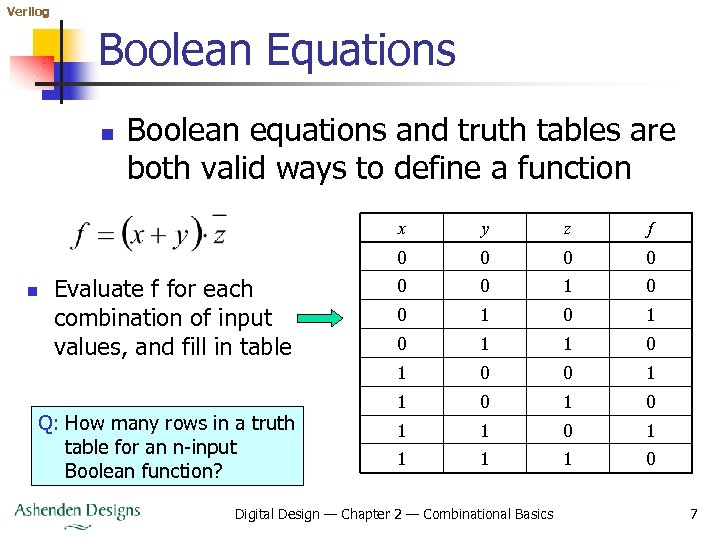
Verilog Boolean Equations n Boolean equations and truth tables are both valid ways to define a function x Q: How many rows in a truth table for an n-input Boolean function? f 0 0 0 1 0 1 0 1 Evaluate f for each combination of input values, and fill in table z 0 n y 0 0 1 1 1 1 0 Digital Design — Chapter 2 — Combinational Basics 7
Verilog Minterms n Given a truth table n For each rows where function value is 1, form a minterm: AND of n n n variables where input is 1 NOT of variables where input is 0 Form OR of minterms x y z f 0 0 0 1 0 1 1 0 1 1 0 Digital Design — Chapter 2 — Combinational Basics 8
Verilog P-terms n This is in sum-of-products form n n logical OR of p-terms (product terms) Not all p-terms are minterms n eg, the following also defines f Digital Design — Chapter 2 — Combinational Basics 9
Verilog Equivalence n n These expressions all represent the same Boolean function The expressions are equivalent n Consistent substitution of variable values gives the same values for the expressions Digital Design — Chapter 2 — Combinational Basics 10
Verilog Optimization n Equivalence allows us to optimize n n choose a different circuit that implements the same function more cheaply Caution: smaller gate count is not always better n choice depends on constraints that apply Digital Design — Chapter 2 — Combinational Basics 11
Verilog Complex Gates n All Boolean functions can be implemented using AND, OR and NOT n But other complex gates may meet constraints better in some fabrics NOR NAND XOR XNOR AND-ORINVERT 0 1 1 0 1 0 1 XNOR y 0 XOR x 0 0 1 1 0 0 0 1 Digital Design — Chapter 2 — Combinational Basics 12
Verilog Complex Gate Example n n These two expressions are equivalent: The NAND-NOR circuit is much smaller and faster in most fabrics! Digital Design — Chapter 2 — Combinational Basics 13
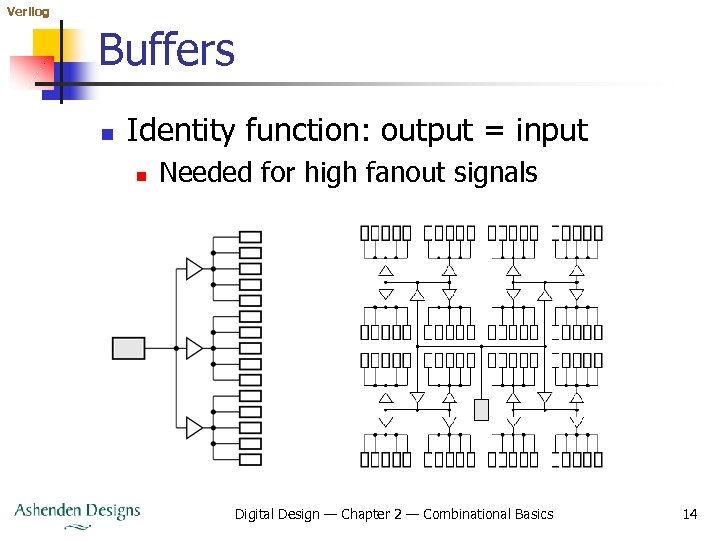
Verilog Buffers n Identity function: output = input n Needed for high fanout signals Digital Design — Chapter 2 — Combinational Basics 14
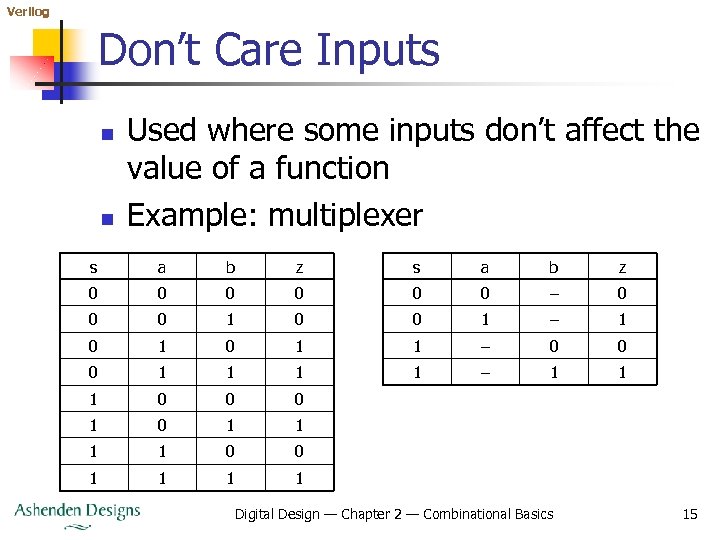
Verilog Don’t Care Inputs n n Used where some inputs don’t affect the value of a function Example: multiplexer s a b z 0 0 0 – 0 0 0 1 – 1 0 1 1 – 0 0 0 1 1 – 1 1 1 0 0 0 1 1 1 1 0 0 1 1 Digital Design — Chapter 2 — Combinational Basics 15
Verilog Don’t Care Outputs n For input combinations that can’t arise n n don’t care if output is 0 or 1 let the synthesis tool choose a b c f f 1 f 2 0 0 0 – 0 1 0 0 0 0 1 1 1 0 0 0 1 0 0 – 0 1 1 1 1 0 0 0 Digital Design — Chapter 2 — Combinational Basics 16
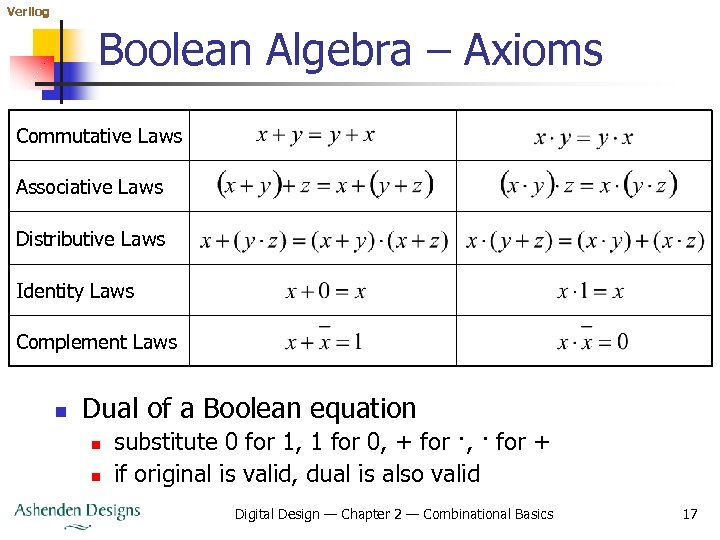
Verilog Boolean Algebra – Axioms Commutative Laws Associative Laws Distributive Laws Identity Laws Complement Laws n Dual of a Boolean equation n n substitute 0 for 1, 1 for 0, + for ·, · for + if original is valid, dual is also valid Digital Design — Chapter 2 — Combinational Basics 17
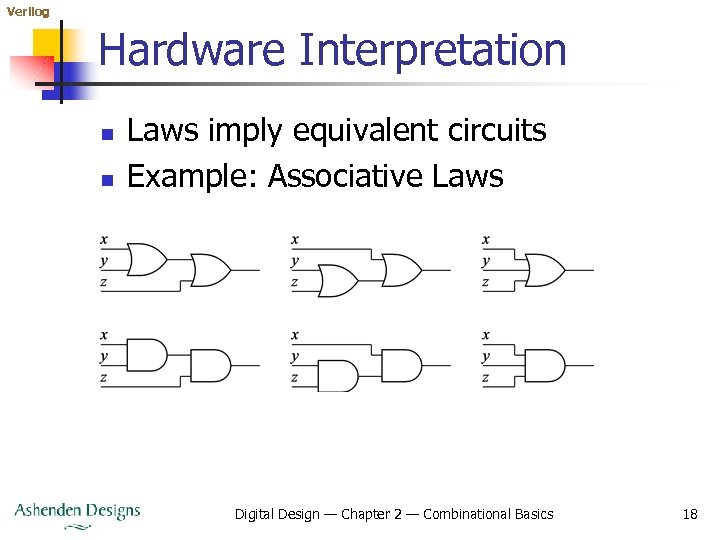
Verilog Hardware Interpretation n n Laws imply equivalent circuits Example: Associative Laws Digital Design — Chapter 2 — Combinational Basics 18
Verilog More Useful Laws Idempotence Laws Identity Laws Absorption Laws De. Morgan Laws Digital Design — Chapter 2 — Combinational Basics 19
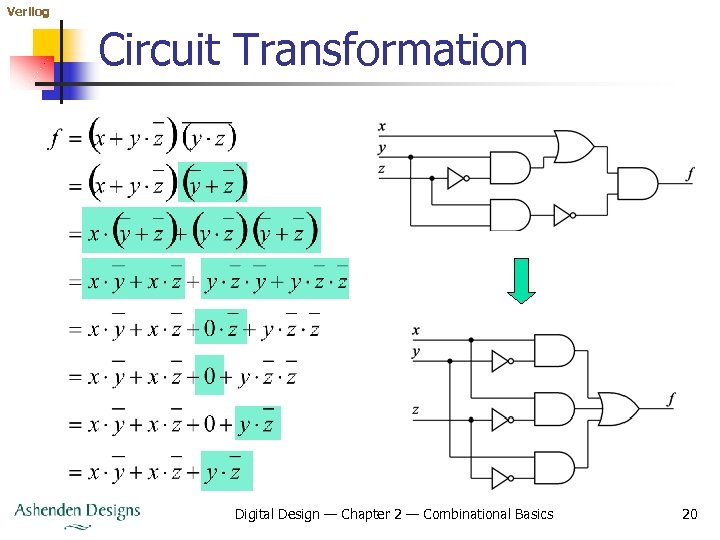
Verilog Circuit Transformation Digital Design — Chapter 2 — Combinational Basics 20
Verilog Optimization Methods n n n How do we decide which Law to apply? What are we trying to optimize? Methods n Karnaugh maps, Quine-Mc. Clusky n n Espresso, Espresso-II, … n n n minimize gate count multi-output minimization Manual methods are only tractable for small circuits Useful methods are embedded in EDA tools n We just specify constraints Digital Design — Chapter 2 — Combinational Basics 21
Verilog Boolean Equations in Verilog n Use logical operators in assignment statements module circuit ( output f, input x, y, z ); assign f = (x | (y & ~z)) & ~(y & z); endmodule Digital Design — Chapter 2 — Combinational Basics 22
Verilog Logical Operators a & b n Precedence n a | b n ~(a & b) n ~(a | b) a ^ b a ~^ b n not has highest then &, then ^ and ~^, then | use parentheses to make order of evaluation clear Verilog bit values n 1'b 0 and 1'b 1 ~a Digital Design — Chapter 2 — Combinational Basics 23
Verilog Boolean Equation Example n Air conditioner control logic n n n heater_on = temp_low · auto_temp + manual_heat cooler_on = temp_high · auto_temp + manual_cool fan_on = heater_on + cooler_on + manual_fan module aircon ( output heater_on, cooler_on, fan_on, input temp_low, temp_high, auto_temp, input manual_heat, manual_cool, manual_fan ); assign heater_on = (temp_low & auto_temp) | manual_heat; assign cooler_on = (temp_high & auto_temp) | manual_cool; assign fan_on = heater_on | cooler_on | manual_fan; endmodule Digital Design — Chapter 2 — Combinational Basics 24
Verilog Binary Coding n How do we represent information with more than two possible values? n n eg, numbers N voltage levels? — No. Multiple binary signals (multiple bits) (a 1, a 0): (0, 0), (0, 1), (1, 0), (1, 1) n n n This is a binary code Each pair of values is a code word Uses two signal wires for a 1, a 0 Digital Design — Chapter 2 — Combinational Basics 25
Verilog Code Word Size n n An n-bit code has 2 n code words To represent N possible values n n n Need at least log 2 N code word bits More bits can be useful in some cases Example: code for inkjet printer n n n black, cyan, magenta, yellow, red, blue six values, log 26 = 3 black: (0, 0, 1), cyan: (0, 1, 0), magenta: (0, 1, 1), yellow: (1, 0, 0), red: (1, 0, 1), blue: (1, 1, 0) Digital Design — Chapter 2 — Combinational Basics 26
Verilog One-Hot Codes n n Each code word has exactly one 1 bit Traffic light: n n n red: (1, 0, 0), yellow: (0, 1, 0), green: (0, 0, 1) Three signal wires: red, yellow, green Each bit of a one-hot code corresponds to an encoded value n No hardware needed to decode values Digital Design — Chapter 2 — Combinational Basics 27
Verilog Binary Codes in Verilog n Multiple bits represented by a vector n wire [4: 0] w; n This is a five-element wire w[4], w[3], w[2], w[1], w[0] wire [1: 3] a; n n n This is a three-element wire n A[1], a[2], a[3] Digital Design — Chapter 2 — Combinational Basics 28
Verilog Binary Coding Example n Traffic-light controller with 1 -hot code n n enable == 1: lights_out = lights_in enable == 0: lights_out = (0, 0, 0) module light_controller_and_enable ( output [1: 3] lights_out, input [1: 3] lights_in, input enable ); assign lights_out[1] = lights_in[1] & enable; assign lights_out[2] = lights_in[2] & enable; assign lights_out[3] = lights_in[3] & enable; endmodule Digital Design — Chapter 2 — Combinational Basics 29
![Verilog Binary Coding Example module light_controller_conditional_enable ( output [1: 3] lights_out, input [1: 3]](https://present5.com/presentation/35a4ae4646286d4b4f66e3640067bd7d/image-30.jpg "Verilog Binary Coding Example module light_controller_conditional_enable ( output [1: 3] lights_out, input [1: 3]")
Verilog Binary Coding Example module light_controller_conditional_enable ( output [1: 3] lights_out, input [1: 3] lights_in, input enable ); assign lights_out = enable ? lights_in : 3'b 000; endmodule Digital Design — Chapter 2 — Combinational Basics 30
Verilog Bit Errors n Electrical noise can change logic levels n n If flipped signal is in a code word n n Bit flip: 0 → 1, 1 → 0 result may be a different code word or an invalid code word inkjet printer, blue: (1, 1, 0) → ? : (1, 1, 1) Could ignore the possibility of a bit flip n n don’t specify behavior of circuit ok if probability is low, effect isn’t disastrous, and application is cost sensitive Digital Design — Chapter 2 — Combinational Basics 31
Verilog Fail-Safe Design n Detect illegal code words n n produce a safe result Traffic-light controller with 1 -hot code n illegal code red light Digital Design — Chapter 2 — Combinational Basics 32
Verilog Redundant Codes n Include extra error code words n n n each differs from a valid code word by a bit -flip ensure no two valid code words are a bitflip apart Detect error code words n n take exceptional action eg, stop, error light, etc Digital Design — Chapter 2 — Combinational Basics 33
Verilog Parity n n Extend a code word with a parity bit Even parity: even number of 1 bits n n Odd parity: odd number of 1 bits n n 001010111, 10010 To check for bit flip, count the 1 s n n 001010110, 100100011 even parity: 001010110 → 000010110 What if there are two bit flips? n even parity: 001010110 → 000110110 Digital Design — Chapter 2 — Combinational Basics 34
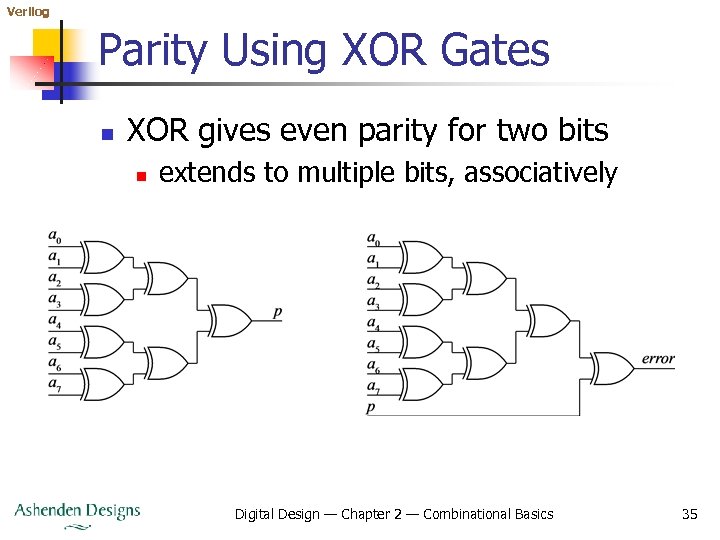
Verilog Parity Using XOR Gates n XOR gives even parity for two bits n extends to multiple bits, associatively Digital Design — Chapter 2 — Combinational Basics 35
Verilog Combinational Components n We can build complex combination components from gates n n Decoders, encoders Multiplexers … Use them as subcomponents of larger systems n Abstraction and reuse Digital Design — Chapter 2 — Combinational Basics 36
Verilog Decoders n A decoder derives control signals from a binary coded signal n n n For an n-bit code input n n One per code word Control signal is 1 when input has the corresponding code word; 0 otherwise Decoder has 2 n outputs Example: (a 3, a 2, a 1) n Output for (1, 0, 1, 1): Digital Design — Chapter 2 — Combinational Basics 37
Verilog Decoder Example Color Codeword (c 2, c 1, c 0) black 0, 0, 1 cyan 0, 1, 0 magenta 0, 1, 1 yellow 1, 0, 0 red 1, 0, 1 blue 1, 1, 0 Digital Design — Chapter 2 — Combinational Basics 38
Verilog Decoder Example module ink_jet_decoder ( output black, cyan, magenta, yellow, light_cyan, light_magenta, input color 2, color 1, color 0 ); assign assign black cyan magenta yellow light_cyan light_magenta = ~color 2 & ~color 1 & color 0; = ~color 2 & color 1 & ~color 0; = ~color 2 & color 1 & color 0; = color 2 & ~color 1 & ~color 0; = color 2 & ~color 1 & color 0; = color 2 & color 1 & ~color 0; endmodule Digital Design — Chapter 2 — Combinational Basics 39
Verilog Encoders n An encoder encodes which of several inputs is 1 n n Assuming (for now) at most one input is 1 at a time What if no input is 1? n Separate output to indicate this condition Digital Design — Chapter 2 — Combinational Basics 40
Verilog Encoder Example Zone n Zone 1 0, 0, 0 Zone 2 0, 0, 1 Zone 3 0, 1, 0 Zone 4 0, 1, 1 Zone 5 1, 0, 0 Zone 6 1, 0, 1 Zone 7 1, 1, 0 Zone 8 Burglar alarm: encode which zone is active Codeword 1, 1, 1 Digital Design — Chapter 2 — Combinational Basics 41
![Verilog Encoder Example module alarm_eqn ( output [2: 0] intruder_zone, output valid, input [1:](https://present5.com/presentation/35a4ae4646286d4b4f66e3640067bd7d/image-42.jpg "Verilog Encoder Example module alarm_eqn ( output [2: 0] intruder_zone, output valid, input [1:")
Verilog Encoder Example module alarm_eqn ( output [2: 0] intruder_zone, output valid, input [1: 8] zone ); assign intruder_zone[2] = zone[5] zone[7] assign intruder_zone[1] = zone[3] zone[7] assign intruder_zone[0] = zone[2] zone[6] | | | zone[6] | zone[8]; zone[4] | zone[8]; assign valid = zone[1] | zone[2] | zone[3] | zone[4] | zone[5] | zone[6] | zone[7] | zone[8]; endmodule Digital Design — Chapter 2 — Combinational Basics 42
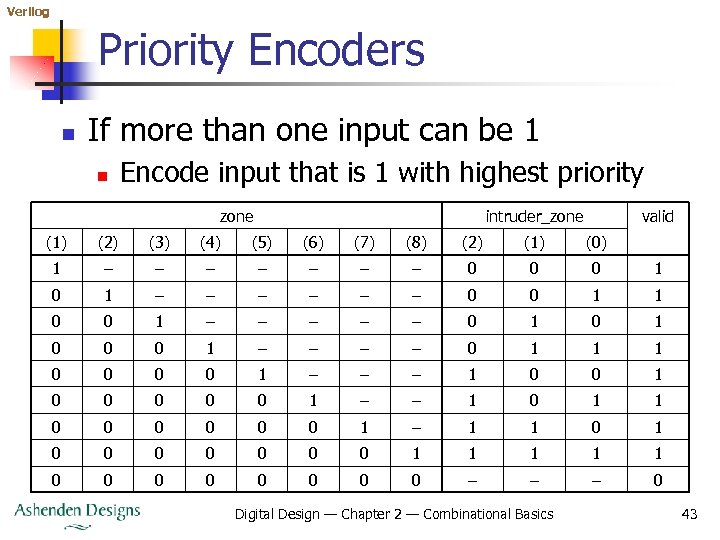
Verilog Priority Encoders n If more than one input can be 1 n Encode input that is 1 with highest priority zone intruder_zone valid (1) (2) (3) (4) (5) (6) (7) (8) (2) (1) (0) 1 – – – – 0 0 0 1 – – – 0 0 1 1 0 0 1 – – – 0 1 0 0 0 1 – – 0 1 1 1 0 0 1 – – – 1 0 0 0 0 0 1 – – 1 0 1 1 0 0 0 1 – 1 1 0 0 0 0 1 1 1 0 0 0 0 – – – 0 Digital Design — Chapter 2 — Combinational Basics 43
![Verilog Priority Encoder Example module alarm_priority_1 ( output [2: 0] intruder_zone, output valid, input](https://present5.com/presentation/35a4ae4646286d4b4f66e3640067bd7d/image-44.jpg "Verilog Priority Encoder Example module alarm_priority_1 ( output [2: 0] intruder_zone, output valid, input")
Verilog Priority Encoder Example module alarm_priority_1 ( output [2: 0] intruder_zone, output valid, input [1: 8] zone ); assign intruder_zone = zone[1] zone[2] zone[3] zone[4] zone[5] zone[6] zone[7] zone[8] 3'b 000; ? ? ? ? 3'b 000 3'b 001 3'b 010 3'b 011 3'b 100 3'b 101 3'b 110 3'b 111 : : : : assign valid = zone[1] | zone[2] | zone[3] | zone[4] | zone[5] | zone[6] | zone[7] | zone[8]; endmodule Digital Design — Chapter 2 — Combinational Basics 44
Verilog BCD Code n Binary coded decimal n 0: 0000 5: 0101 4 -bit code for decimal digits 1: 0001 6: 0110 2: 0010 7: 0111 3: 0011 8: 1000 4: 0100 9: 1001 Digital Design — Chapter 2 — Combinational Basics 45
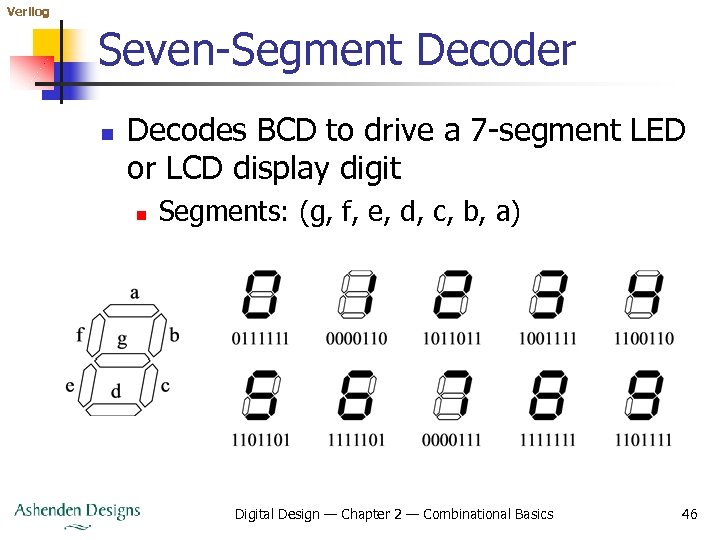
Verilog Seven-Segment Decoder n Decodes BCD to drive a 7 -segment LED or LCD display digit n Segments: (g, f, e, d, c, b, a) Digital Design — Chapter 2 — Combinational Basics 46
![Verilog Seven-Segment Decoder module seven_seg_decoder ( output [7: 1] seg, input [3: 0] bcd,](https://present5.com/presentation/35a4ae4646286d4b4f66e3640067bd7d/image-47.jpg "Verilog Seven-Segment Decoder module seven_seg_decoder ( output [7: 1] seg, input [3: 0] bcd,")
Verilog Seven-Segment Decoder module seven_seg_decoder ( output [7: 1] seg, input [3: 0] bcd, input blank ); reg [7: 1] seg_tmp; always @* case (bcd) 4'b 0000: 4'b 0001: 4'b 0010: 4'b 0011: 4'b 0100: 4'b 0101: 4'b 0110: 4'b 0111: 4'b 1000: 4'b 1001: default: endcase seg_tmp seg_tmp seg_tmp = = = 7'b 0111111; 7'b 0000110; 7'b 1011011; 7'b 1001111; 7'b 1100110; 7'b 1101101; 7'b 1111101; 7'b 0000111; 7'b 1111111; 7'b 1101111; 7'b 1000000; // // // 0 1 2 3 4 5 6 7 8 9 "-" for invalid code assign seg = blank ? 7'b 0000000 : seg_tmp; endmodule Digital Design — Chapter 2 — Combinational Basics 47
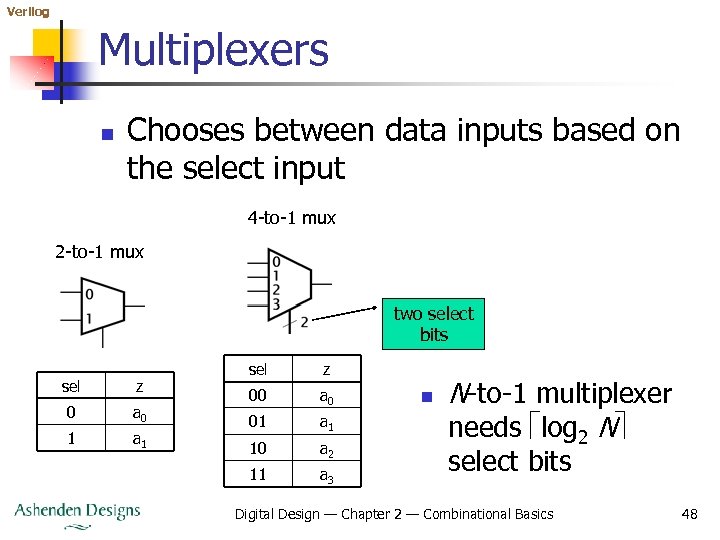
Verilog Multiplexers n Chooses between data inputs based on the select input 4 -to-1 mux 2 -to-1 mux two select bits sel z 0 a 0 1 a 1 sel z 00 a 0 01 a 1 10 a 2 11 a 3 n N-to-1 multiplexer needs log 2 N select bits Digital Design — Chapter 2 — Combinational Basics 48
![Verilog Multiplexer Example module multiplexer_4_to_1 ( output reg z, input [3: 0] a, input](https://present5.com/presentation/35a4ae4646286d4b4f66e3640067bd7d/image-49.jpg "Verilog Multiplexer Example module multiplexer_4_to_1 ( output reg z, input [3: 0] a, input")
Verilog Multiplexer Example module multiplexer_4_to_1 ( output reg z, input [3: 0] a, input sel ); always @* case (sel) 2'b 00: z 2'b 01: z 2'b 10: z 2'b 11: z endcase = = a[0]; a[1]; a[2]; a[3]; endmodule Digital Design — Chapter 2 — Combinational Basics 49
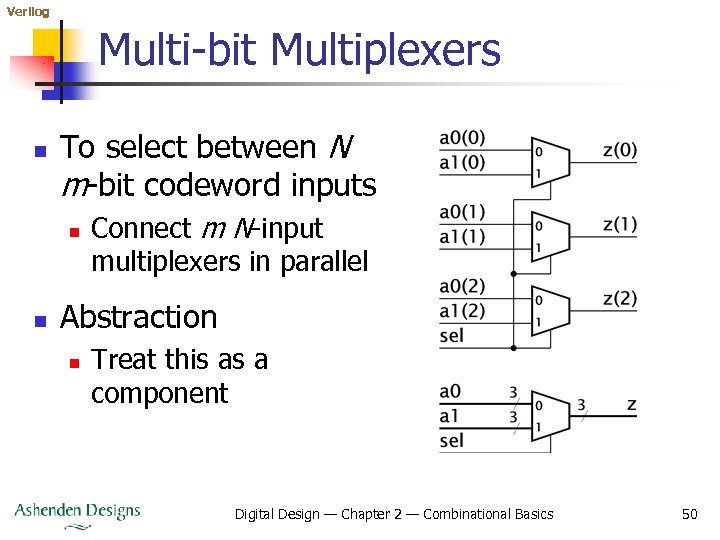
Verilog Multi-bit Multiplexers n To select between N m-bit codeword inputs n n Connect m N-input multiplexers in parallel Abstraction n Treat this as a component Digital Design — Chapter 2 — Combinational Basics 50
![Verilog Multi-bit Mux Example module multiplexer_3 bit_2_to_1 ( output [2: 0] z, input [2:](https://present5.com/presentation/35a4ae4646286d4b4f66e3640067bd7d/image-51.jpg "Verilog Multi-bit Mux Example module multiplexer_3 bit_2_to_1 ( output [2: 0] z, input [2:")
Verilog Multi-bit Mux Example module multiplexer_3 bit_2_to_1 ( output [2: 0] z, input [2: 0] a 0, a 1, input sel ); assign z = sel ? a 1 : a 0; endmodule Digital Design — Chapter 2 — Combinational Basics 51
Verilog Active-Low Logic n We’ve been using active-high logic n n n 0 (low voltage): falsehood of a condition 1 (high voltage): truth of a condition Active-low logic 0 (low voltage): truth of a condition n 1 (high voltage): falsehood of a condition n reverses the representation, not negative voltage! In circuit schematics, label active-low signals with overbar notation n eg, lamp_lit: low when lit, high when not lit Digital Design — Chapter 2 — Combinational Basics 52
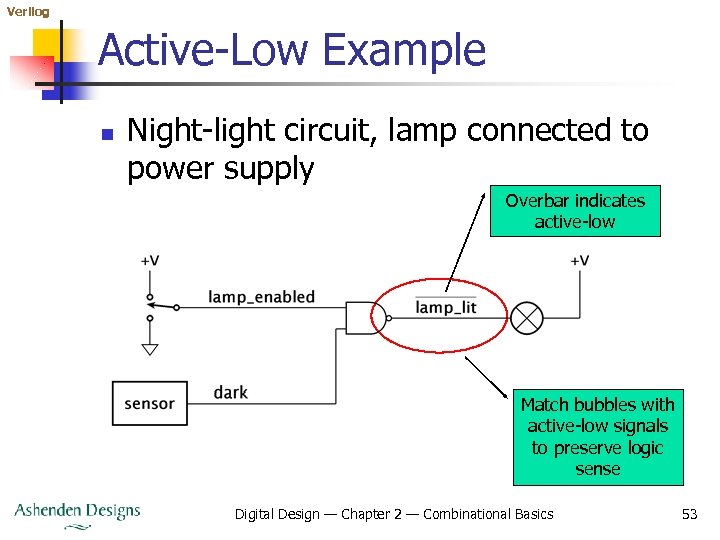
Verilog Active-Low Example n Night-light circuit, lamp connected to power supply Overbar indicates active-low Match bubbles with active-low signals to preserve logic sense Digital Design — Chapter 2 — Combinational Basics 53
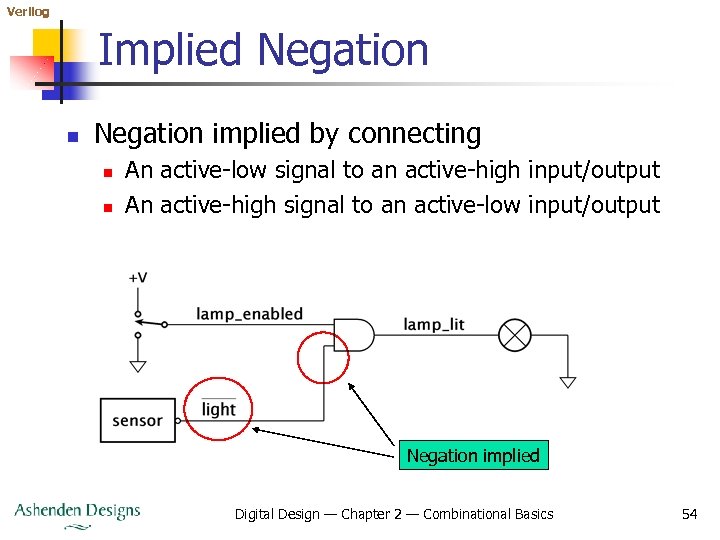
Verilog Implied Negation n Negation implied by connecting n n An active-low signal to an active-high input/output An active-high signal to an active-low input/output Negation implied Digital Design — Chapter 2 — Combinational Basics 54
Verilog Active-Low Signals and Gates n De. Morgan’s laws suggest alternate views for gates n n n They’re the same electrical circuit! Use the view that best represents the logical function intended Match the bubbles, unless implied negation is intended Digital Design — Chapter 2 — Combinational Basics 55
Verilog Active-Low Logic in Verilog n Can’t draw an overbar in Verilog n n n 1'b 0 and 1'b 1 in Verilog mean low and high For active-low logic n n n Use _N suffix on signal or port name 1'b 0 means the condition is true 1'b 1 means the condition is false Example n n assign lamp_lit_N = 1'b 0; turns the lamp on Digital Design — Chapter 2 — Combinational Basics 56
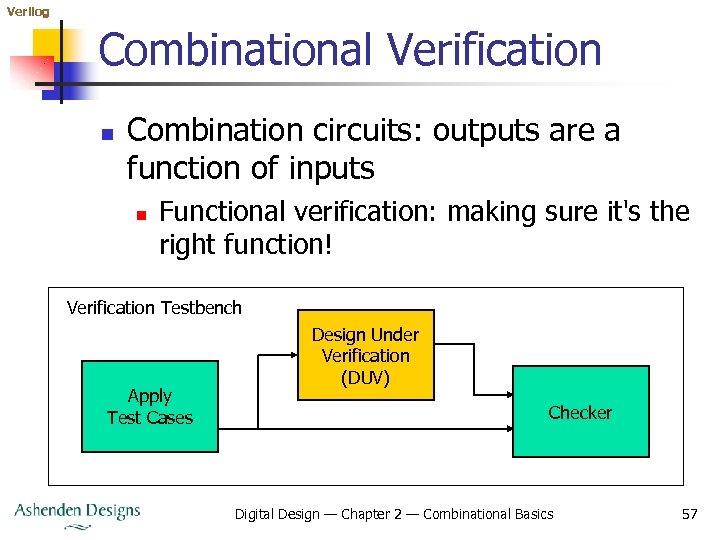
Verilog Combinational Verification n Combination circuits: outputs are a function of inputs n Functional verification: making sure it's the right function! Verification Testbench Apply Test Cases Design Under Verification (DUV) Checker Digital Design — Chapter 2 — Combinational Basics 57
Verilog Verification Example n n Verify operation of traffic-light controller Property to check n n n enable lights_out == lights_in !enable all lights are inactive Represent this as an assertion in the checker Digital Design — Chapter 2 — Combinational Basics 58
![Verilog Testbench Module `timescale 1 ms/1 ms module light_testbench; wire [1: 3] lights_out; reg](https://present5.com/presentation/35a4ae4646286d4b4f66e3640067bd7d/image-59.jpg "Verilog Testbench Module `timescale 1 ms/1 ms module light_testbench; wire [1: 3] lights_out; reg")
Verilog Testbench Module `timescale 1 ms/1 ms module light_testbench; wire [1: 3] lights_out; reg [1: 3] lights_in; reg enable; light_controller_and_enable duv (. lights_out(lights_out), . lights_in(lights_in), . enable(enable) ); Digital Design — Chapter 2 — Combinational Basics 59
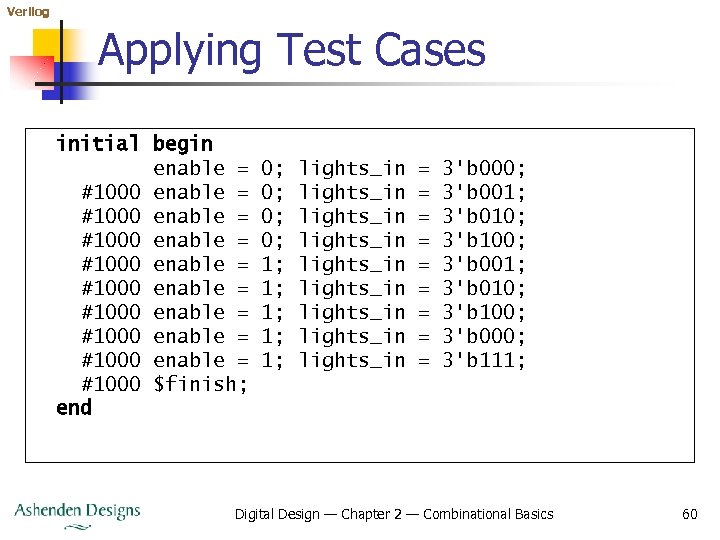
Verilog Applying Test Cases initial begin enable = #1000 enable = #1000 enable = #1000 $finish; end 0; 0; 1; 1; 1; lights_in lights_in lights_in = = = = = 3'b 000; 3'b 001; 3'b 010; 3'b 100; 3'b 000; 3'b 111; Digital Design — Chapter 2 — Combinational Basics 60
Verilog Checking Assertions always @(enable or lights_in) begin #10 if (!( ( enable && lights_out == lights_in) || (!enable && lights_out == 3'b 000) )) $display("Error in light controller output"); endmodule Digital Design — Chapter 2 — Combinational Basics 61
Verilog Functional Coverage n n Did we test all possible input cases? For large designs, exhaustive testing is not tractable n n N inputs: number of cases = 2 N Functional coverage n n Proportion of test cases covered by a testbench It can be hard to decide how much testing is enough Digital Design — Chapter 2 — Combinational Basics 62
Verilog Summary n n Combinational logic: output values depend only on current input values Boolean functions: defined by truth tables and Boolean equations Equivalence of functions optimization Binary codes used to represent information with more than two values Digital Design — Chapter 2 — Combinational Basics 63
Verilog Summary n Combinational components n n n gates: AND, OR, inverter, 2 -to-1 mux complex gates: NAND, NOR, XNOR, AOI decoder, encoder, priority encoder Active-low logic Verification testbench n n apply test cases to DUV checker contains assertions Digital Design — Chapter 2 — Combinational Basics 64
Скачать презентацию Digital Design An Embedded Systems Approach Using Verilog
35a4ae4646286d4b4f66e3640067bd7d.ppt