Difusión y sedimentación Difusión Primera ley de Fick

Difusión y sedimentación Difusión Primera ley de Fick de la difusión Coeficiente de difusión Desplazamiento neto de moléculas de se difunden Desplazamiento neto de partículas coloidales: Movimiento Browniano Teoría de la difusión en líquidos Sedimentación de moléculas poliméricas en disolución Fisicoquímica, Ira N. Levine, (Mc. Graw Hill, Madrid, 2004). Capítulo 16. En este capítulo se usan figuras dinámicas producidas por Zoltán Erdelyi Copyright: "This material originally created by Zoltán ERDÉLYI and published on the http: //dragon. unideb. hu/~zerdelyi web site. “ y otros. Los enlaces correspondientes aparecen próximos a las figuras. UAM 2012 -13. Química Física. Transporte - Difusión 1

Difusión x→ P P tabique desmontable Difusión de las sustancias j y k contenidas en un tanque Fase 1 Fase 2 cj, 1 , ck, 1 cj, 2 , ck, 2 área A baño a T constante § concentraciones iniciales: cj, 1 cj, 2 ; ck, 1 ck, 2 § se retira el tabique § se observa que el movimiento al azar de moléculas elimina la diferencia de concentraciones Difusión es el movimiento macroscópico de componentes de un sistema debido a diferencias de concentración cj t=0 cj x→ t=t x→ cj t= x→ UAM 2012 -13. Química Física. http: //dragon. unideb. hu/~zerdelyi/Diffusion-on-the-nanoscale/node 6. html Transporte - Difusión 2

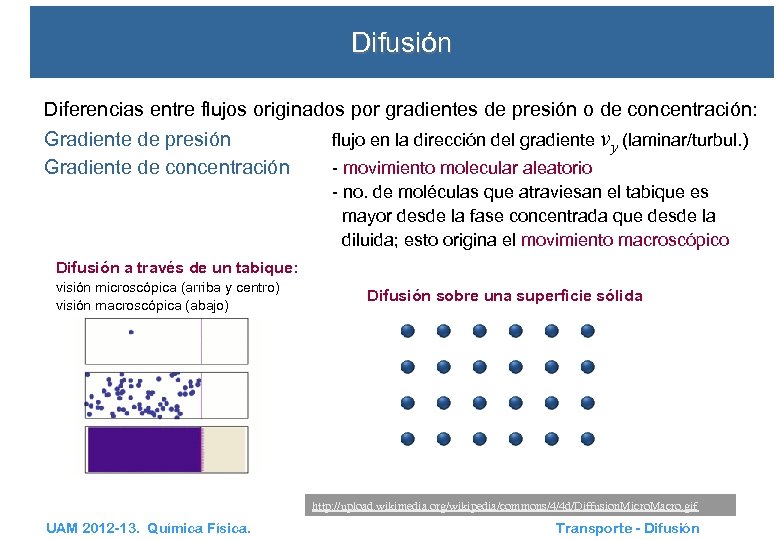Difusión Diferencias entre flujos originados por gradientes de presión o de concentración: Gradiente de presión Gradiente de concentración flujo en la dirección del gradiente vy (laminar/turbul. ) - movimiento molecular aleatorio - no. de moléculas que atraviesan el tabique es mayor desde la fase concentrada que desde la diluida; esto origina el movimiento macroscópico Difusión a través de un tabique: visión microscópica (arriba y centro) visión macroscópica (abajo) Difusión sobre una superficie sólida http: //upload. wikimedia. org/wikipedia/commons/4/4 d/Diffusion. Micro. Macro. gif UAM 2012 -13. Química Física. http: //upload. wikimedia. org/wikipedia/commons/7/74/Surface_chemical_diffusion. gif Transporte - Difusión 3

Difusión (visión estática) mayor no. de moléculas → Movimiento molecular en la difusión Difusión en una superficie sólida http: //upload. wikimedia. org/wikipedia/commons/4/4 d/Diffusion. Micro. Macro. gif http: //upload. wikimedia. org/wikipedia/commons/7/74/Surface_chemical_diffusion. gif UAM 2012 -13. Química Física. Transporte - Difusión 4

Primera ley de Fick de la difusión x→ P P tabique desmontable Se observa transporte de materia: Fase 1 Fase 2 cj, 1 , ck, 1 cj, 2 , ck, 2 área A A A baño a T constante dcj /dx = gradiente de concentración en un plano transversal dnj /dt = velocidad de flujo de j, en mol/s, a través de un plano perpendicular a x de superfice A Djk = coeficiente de difusión mutuo [=] área/tiempo: cm 2/s. Depende del estado signo ‒ local del sistema: P, T, composición flujo del componente hacia zonas donde la concentración es menor: dnj /dt<0 cuando dcj /dx>0 UAM 2012 -13. Química Física. Transporte - Difusión 5

El coeficiente de difusión Djk = coeficiente de difusión mutuo [=] área/tiempo: cm 2/s. Depende del estado local del sistema: P, T, composición § Si cj, 1 y cj, 2 son muy distintas, Djk varía mucho con la concentración: varía mucho con x y t § Si cj, 1 y cj, 2 son similares, su variación con la concentración puede despreciarse: se toma el valor correspondiente a la concentración promedio § Djk = Dkj si los volúmenes mezclados son aditivos: VT V 1 + V 2 (gases o líquidos de composición muy parecida: concentraciones similares) UAM 2012 -13. Química Física. Transporte - Difusión 6

Coeficiente de difusión de algunos materiales Djk al temperatura Gases - al presión valores a 0 o. C, 1 atm Par de gases 10‒ 1 H 2‒O 2 He‒Ar O 2‒N 2 O 2‒CO 2‒CH 4 CO‒C 2 H 4 Djk/(cm 2 s‒ 1) 0. 70 0. 64 0. 18 0. 14 0. 15 0. 12 al T ; varía fuertemente con la composición Disoluciones líquidas Di. B coeficiente de difusión del soluto i en el disolvente B a dilución infinita valores a 25 o. C, 1 atm: i 10‒ 5 N 2 Li. Br Na. Cl n-C 4 H 9 OH sacarosa hemoglobina 105 D i, H 2 O /(cm 2 s‒ 1) 1. 6 1. 4 2. 2 0. 56 0. 52 0. 07 fuertemente al T ; depende de la concentración Sólidos valores a 1 atm i ‒B Sb ‒ Ag Al ‒ Cu Ni ‒ Cu Cu ‒ Ni Temperatura (o. C) 10‒ 20 Bi ‒ Pb 20 20 20 630 1025 D i-B /(cm 2 s‒ 1) 10‒ 16 10‒ 21 10‒ 30 10‒ 13 10‒ 9 10‒ 11 UAM 2012 -13. Química Física. Transporte - Difusión 7

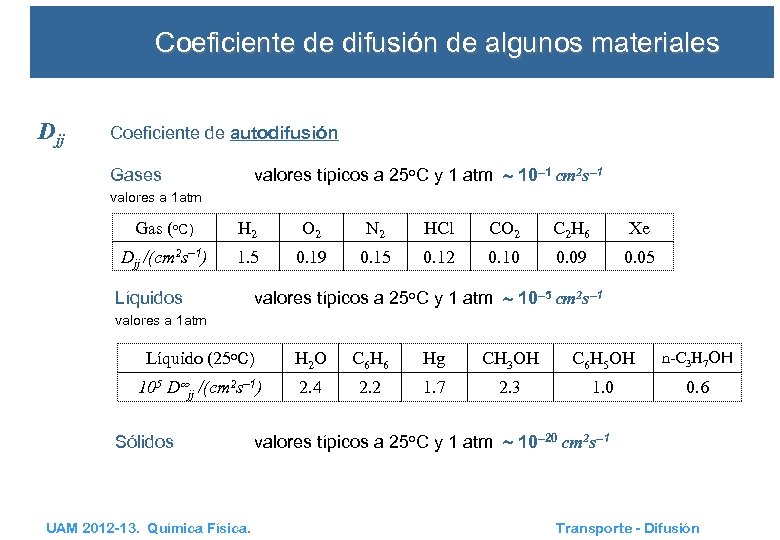Coeficiente de difusión de algunos materiales Djj Coeficiente de autodifusión valores típicos a 25 o. C y 1 atm 10‒ 1 cm 2 s‒ 1 Gases valores a 1 atm Gas (o. C) H 2 O 2 N 2 HCl CO 2 C 2 H 6 Xe Djj /(cm 2 s‒ 1) 1. 5 0. 19 0. 15 0. 12 0. 10 0. 09 0. 05 Líquidos valores típicos a 25 o. C y 1 atm 10‒ 5 cm 2 s‒ 1 valores a 1 atm Líquido (25 o. C) H 2 O C 6 Hg CH 3 OH C 6 H 5 OH n-C 3 H 7 OH 105 D jj /(cm 2 s‒ 1) 2. 4 2. 2 1. 7 2. 3 1. 0 0. 6 Sólidos UAM 2012 -13. Química Física. valores típicos a 25 o. C y 1 atm 10‒ 20 cm 2 s‒ 1 Transporte - Difusión 8

Desplazamiento neto de moléculas que se difunden ¿Qué distancia recorre en promedio una molécula en una dirección dada (x), durante un tiempo t cuando se difunde moviéndose aleatoriamente ? Ecuación de Einstein-Smoluchowski Raíz del desplazamiento cuadrático medio NETO en la dirección x t = 60 s ; T= 298 K ; P = 1 atm Gas Líquido Sólido D /(cm 2 s‒ 1) 10‒ 1 10‒ 5 10‒ 20 ( x)rms /cm 3 0. 03 <1Å http: //dragon. unideb. hu/~zerdelyi/Diffusion-on-the-nanoscale/node 4. html Nota que: en 1 min, una molécula de gas de 30 g/mol recorre un total de 3 106 cm, en esas condiciones de T y P en su movimiento aleatorio !!!! Problemas 8 y 9 UAM 2012 -13. Química Física. Transporte - Difusión 9

Movimiento browniano de partículas coloidales Desplazamiento neto de partículas coloidales en un líquido: movimiento Browniano La difusión se origina por el movimiento térmico aleatorio de las moléculas (masa: m) en un líquido (de viscosidad: ) resultante de: fuerzas sobre la macromolécula (molécula: esfera de radio r) (componente x): § fuerza debida a choques aleatorios con moléculas del líquido: Fx(t) § fuerza de fricción (el líquido se opone al movimiento de la partícula): Ffr, x = f vx = 6 rvx § fuerza total (multiplicada por x) x max = x m d 2 x /dt 2 = x Fx(t) x 6 r vx Movimiento browniano de esferas de latex (diámetro: 20 nm) en agua que promediadas a todas las moléculas y suponiendo que la energía cinética promedio es translacional = 3/2 k. T dan lugar a: Einstein Problema 10 comprobada experimentalmente UAM 2012 -13. Química Física. Otro enlace de interés: http: //www. aip. org/history/einstein/brownian. htm Transporte - Difusión 10

Teoría de la difusión en líquidos Disolución muy diluida: Problema 11 § dilución infinita Einstein-Smoluchowski § moléculas de soluto (i) mucho mayores que las de disolvente (B): Si ri > r. B : UAM 2012 -13. Química Física. Si ri r. B : Ley de Stokes para moléculas esféricas de radio ri aplicable si ri > r. B Si ri < r. B : Transporte - Difusión 11

Sedimentación de moléculas poliméricas en disolución Aplicación: obtención del peso molecular de un polímero (Mi ) Al disolver un soluto polimérico en un disolvente menos denso que él, sus moléculas se sedimentan como resultado de las fuerzas que actúan sobre ellas: (soluto polimérico: i ; disolvente: B) § fuerza gravitacional § fuerza de fricción coef. de fricción: f velocidad de sedimentación: vsed § empuje volumen específico parcial UAM 2012 -13. Química Física. volumen molar parcial Transporte - Difusión 12

Sedimentación de moléculas poliméricas en disolución Si se utiliza una centrífuga cuya aceleración centrífuga es r 2 para acelerar la sedimentación: A dilución infinita, usando la ec. Einstein Smoluchowski: Se obtiene el peso molecular a partir de: § extrapolación a dilución infinita de medidas de velocidades de sedimentación § medidas de coeficientes de difusión “coeficiente de sedimentación”: UAM 2012 -13. Química Física. (suele darse en s o en “Svedverg”= Sv=10 13 s) Problema 12 Transporte - Difusión 13