Дифракция света 1 Дифракцией света называется отклонение

Дифракция света 1

Дифракцией света называется отклонение распространения светового луча от прямолинейного на резких неоднородностях среды 2

Дифракция была открыта Франческо Гримальди в конце XVII в. Объяснение явления дифракции света дано Томасом Юнгом и Огюстом Френелем, которые не только дали описание экспериментов по наблюдению явлений интерференции и дифракции света, но и объяснили свойство прямолинейности распространения света с позиций волновой теории 3

Гримальди Франческо 2. IV. 1618 - 28. XII. 1663 Итальянский ученый. С 1651 года - священник. Открыл дифракцию света, систематически ее изучал и сформулировал некоторые правила. Описал солнечный спектр, полученный с помощью призмы. В 1662 г. определил величину 4 поверхности Земли.

Френель Огюст Жан (10. V. 1788 - 14. VII. 1827) Французский физик. Научные работы посвящены физической оптике. Дополнил известный принцип Гюйгенса, введя так называемые зоны Френеля (принцип Гюйгенса - Френеля). Разработал в 1818 году теорию дифракции света 5

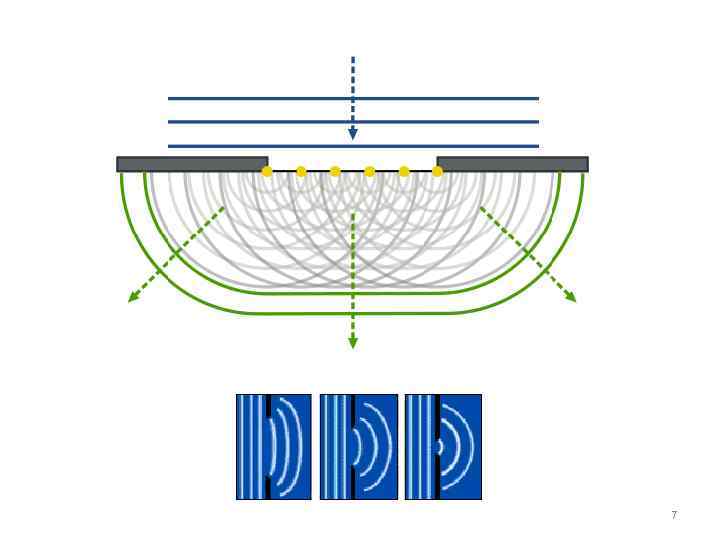
Принцип Гюйгенса-Френеля: Каждый элемент волнового фронта можно рассматривать, как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн. 6

7

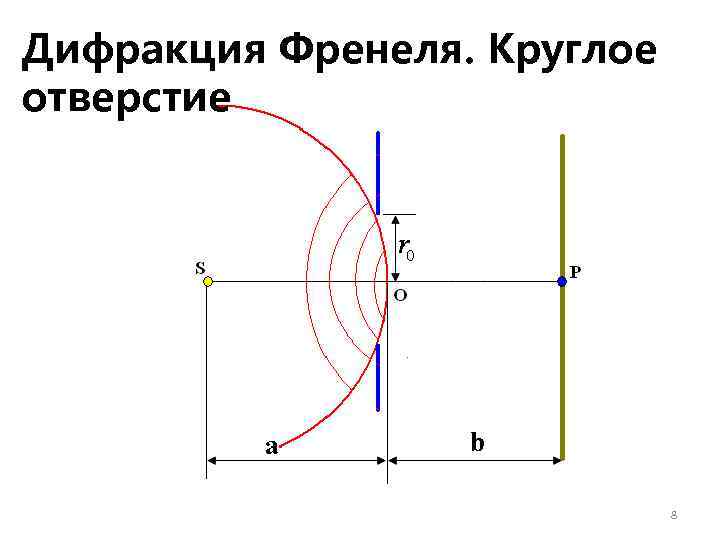Дифракция Френеля. Круглое отверстие 8

Разобьем поверхность волнового фронта, падающего на отверстие, на зоны Френеля по отношению к точке наблюдения P. Будем называть открытыми такие зоны Френеля, которые располагаются внутри отверстия. Соответственно зоны Френеля, попадающие на поверхность непрозрачного экрана, называются закрытыми. 9

Если размер отверстия во много раз меньше расстояний от экрана до источника a и от экрана до точки наблюдения b, то можно найти число m открытых отверстием зон Френеля: 10

Суммарная амплитуда в точке наблюдения есть A 3 – A 4 +. . . A = A 1 – A 2 + ±Am = 0. 5(A 1±Am) Амплитуды волн зон Френеля при их небольшом числе можно считать примерно одинаковыми. 11

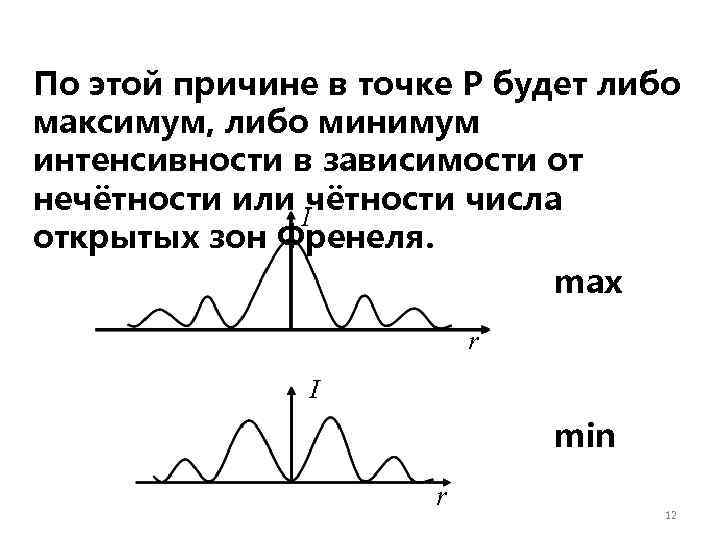По этой причине в точке Р будет либо максимум, либо минимум интенсивности в зависимости от нечётности или чётности числа открытых зон Френеля. max min 12

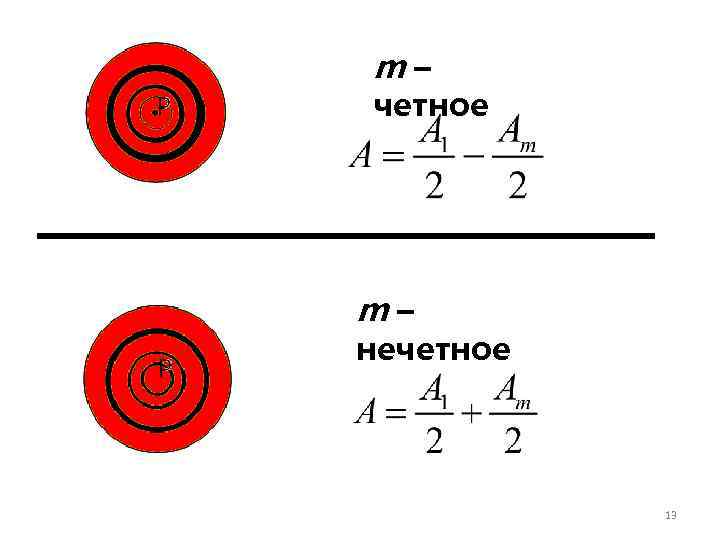m – четное m – нечетное 13

Интенсивность света в максимумах по мере удаления от центральной точки будет убывать. Убывание объясняется тем, что при смещении точки наблюдения P из центра на периферию открытые из точки P центральные зоны Френеля частично закрываются и, кроме того, частично открываются новые зоны Френеля, ослабляющие интенсивность света в точке 14

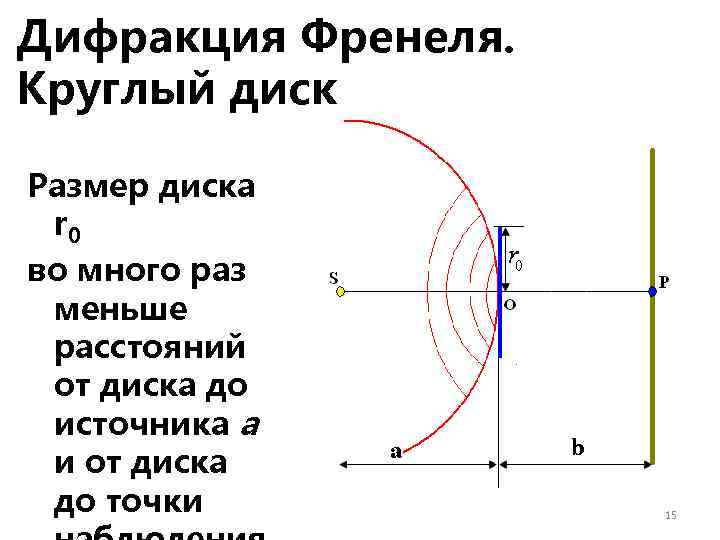Дифракция Френеля. Круглый диск Размер диска r 0 во много раз меньше расстояний от диска до источника a и от диска до точки 15

Диск из точки наблюдения P закрывает m зон Френеля. Тогда амплитуда света A в точке наблюдения будет равна алгебраической сумме амплитуд волн открытых зон Френеля: 16

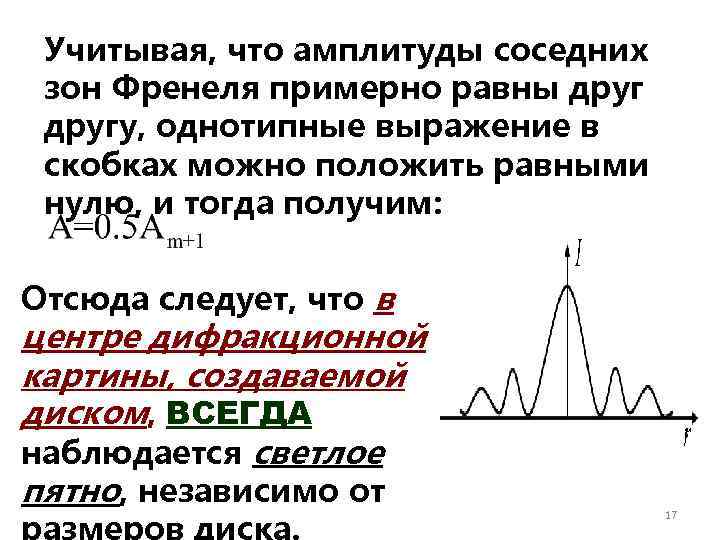Учитывая, что амплитуды соседних зон Френеля примерно равны другу, однотипные выражение в скобках можно положить равными нулю, и тогда получим: Отсюда следует, что в центре дифракционной картины, создаваемой диском, ВСЕГДА наблюдается светлое пятно, независимо от 17

Дифракционная картина от диска, наблюдаемая на экране, имеет характер чередующихся тёмных и светлых колец, в центре Структура дифракционной картины которых находится света от непрозрачного диска имеет светлое пятно. общие черты с дифракционной картиной света от отверстия того же диаметра в непрозрачном экране. 18

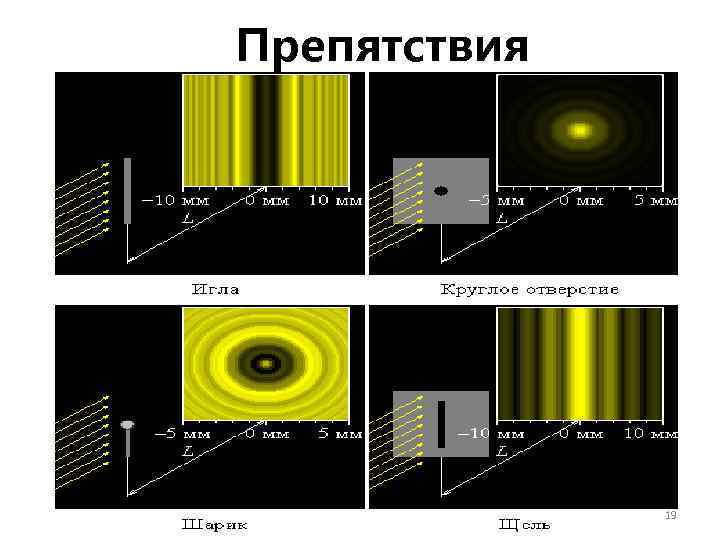Препятствия 19

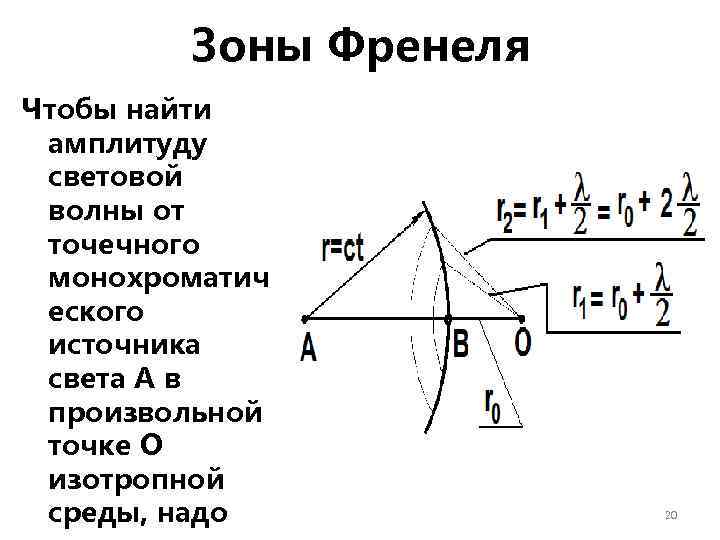Зоны Френеля Чтобы найти амплитуду световой волны от точечного монохроматич еского источника света А в произвольной точке О изотропной среды, надо 20

Интерференция волны от вторичных источников, расположенных на этой поверхности, определяет амплитуду в рассматриваемой точке P, т. е. необходимо произвести сложение когерентных колебаний от всех вторичных источников на волновой поверхности 21

Первая зона Френеля ограничивается точками волновой поверхности, расстояния от которых до точки О равны: где — длина световой волны Вторая зона: Аналогично определяются границы других зон 22

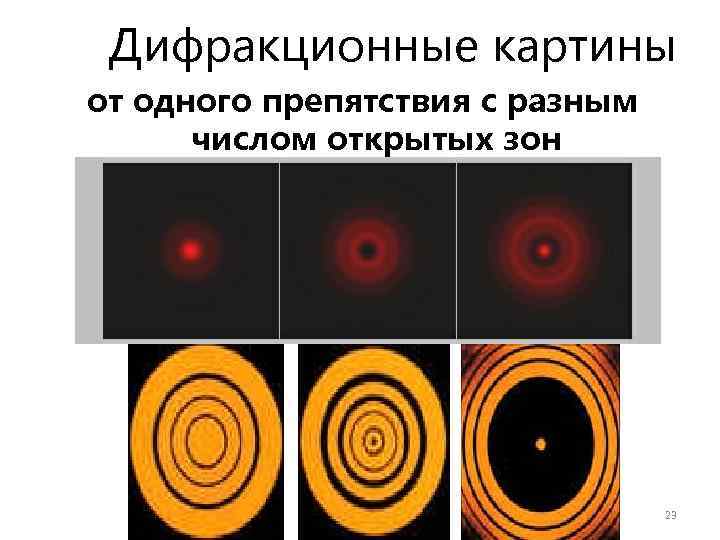Дифракционные картины от одного препятствия с разным числом открытых зон 23

Если на препятствии укладывается целое число длин волн, то они гасят друга и в данной точке наблюдается минимум (темное пятно). Если нечетное число полуволн, то наблюдается максимум (светлое пятно) 24

25

Зонные пластинки На этом принцип е основан ы т. н. зонные пластинк и 26

Фраунгофер Йозеф (6. III. 1787 - 7. VI. 1826) Немецкий физик. Научные работы относятся к физической оптике. Внёс существенный вклад в исследование дисперсии и создание ахроматических линз. Фраунгофер изучал дифракцию в параллельных лучах (так называемая дифракция Фраунгофера). Сначала от одной щели, а потом от многих. Большой заслугой учёного является использование(с 1821 года) дифракционных решеток для 27

Дифракция Фраунгофер Периодическая система одинаковых, расположенных на одном и том же расстоянии друг от друга щелей, называется дифракционной решёткой. Расстояние d между серединами соседних щелей называется периодом дифракционной решётки. Обычно в дифракционных решётках, используемых в оптике, размер b во много раз меньше периода дифракционной решётки d<

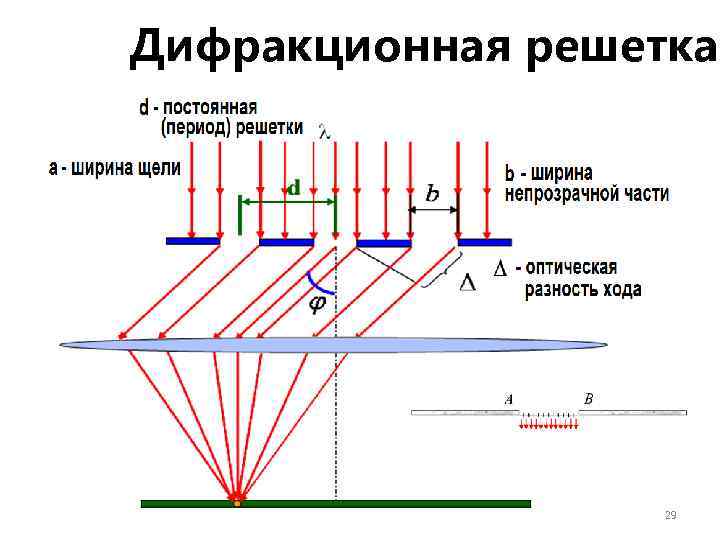Дифракционная решетка 29

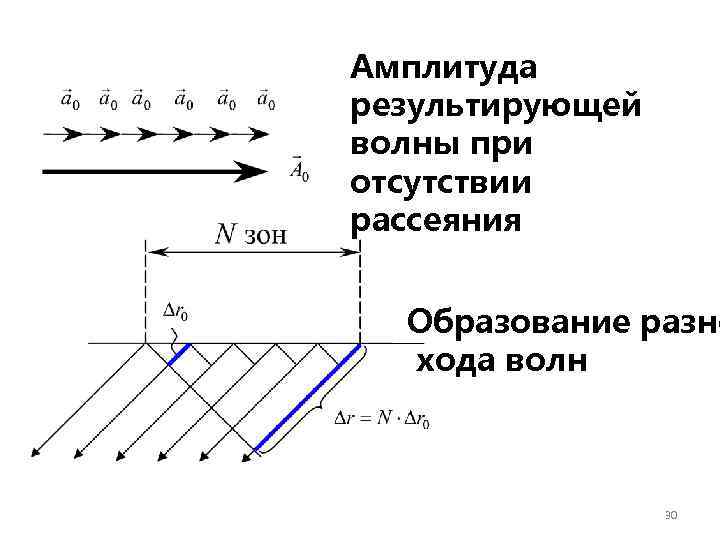Амплитуда результирующей волны при отсутствии рассеяния Образование разно хода волн 30

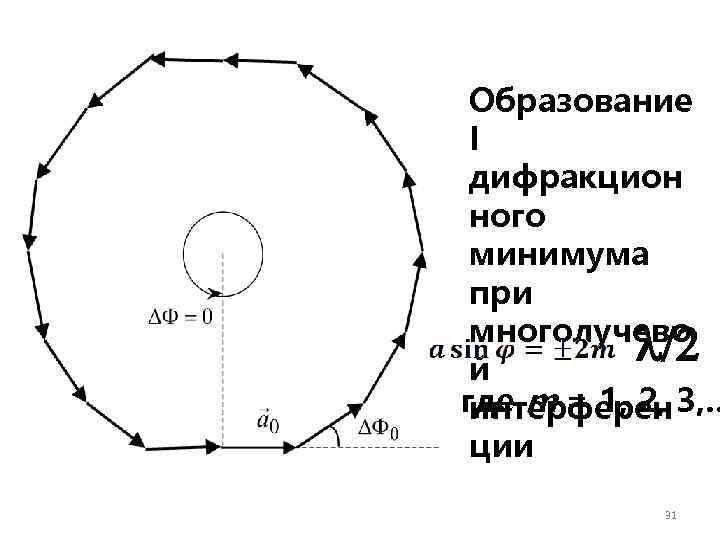Образование I дифракцион ного минимума при многолучево /2 й где m = 1, 2, 3, … интерферен ции 31

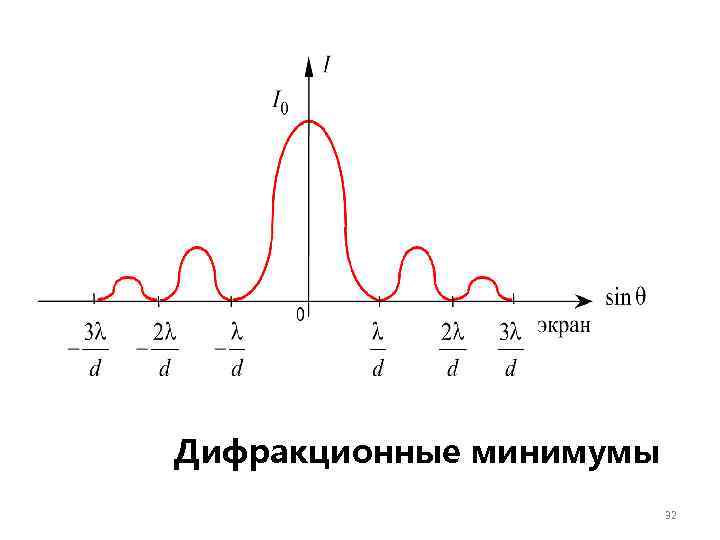Дифракционные минимумы 32

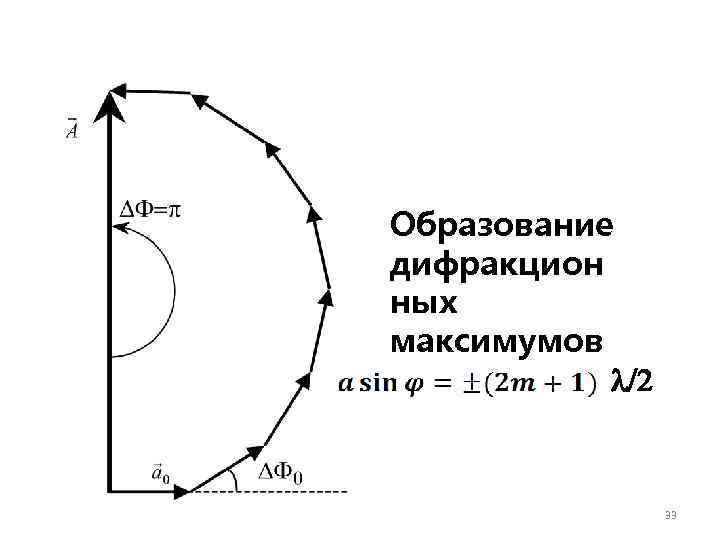Образование дифракцион ных максимумов /2 33

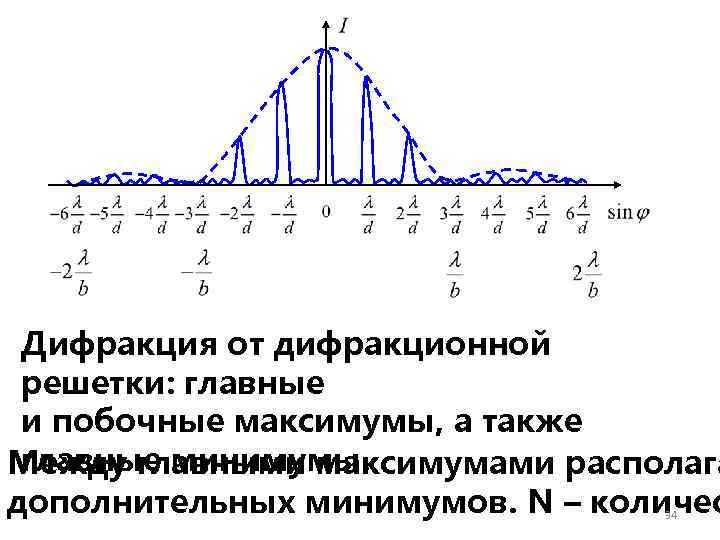Дифракция от дифракционной решетки: главные и побочные максимумы, а также главные минимумы. Между главными максимумами располага дополнительных минимумов. N – количес 34

a sinφ =± 2 m /2 - главные минимумы m= 1, 2, 3 … d sinφ =± 2 m /2 - главные максимумы m= 0, 1, 2, 3 … d sinφ =±(2 m+1) /2 – дополнительные минимумы m=0, 1, 2, 3 … 35

Главные дифракционные максимумы интенсивности располагаются в направлениях φm, в которых волны от щелей в точке наблюдения имеют разность хода, кратную λ. Главный дифракционный максимум, соответствующий направлению, называется дифракционным максимумом m- го порядка. Центральный дифракционный максимум соответственно является дифракционным максимумом нулевого порядка (m=0) и имеет 36

Границы применимости геометрической оптики Дифракция наблюдается хорошо на расстоянии Если , то дифракция невидна и получается резкая тень (d - диаметр экрана). Если наблюдение ведется на расстоянии где d — размер предмета, то начинают проявляться волновые свойства света 37

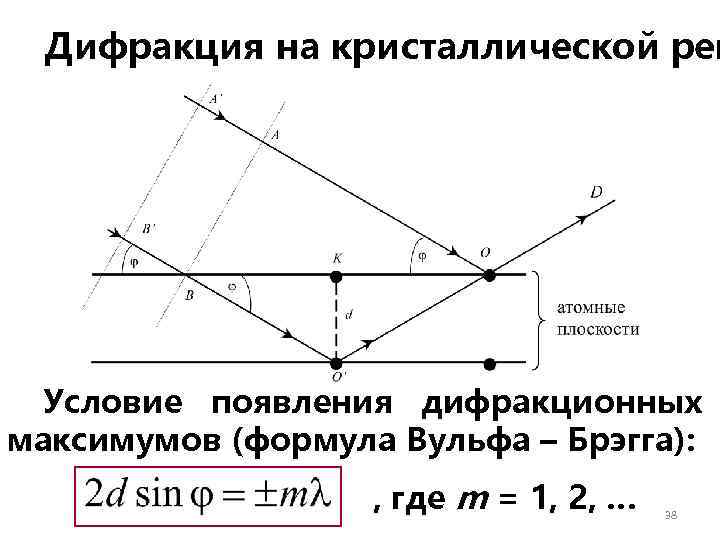Дифракция на кристаллической реш Условие появления дифракционных максимумов (формула Вульфа – Брэгга): , где m = 1, 2, … 38

Разрешающая сила дифракционной решетки Здесь δλ - минимальная разница в длинах волн соседних спектральных линий, при которой эти линии еще можно наблюдать раздельно. 39

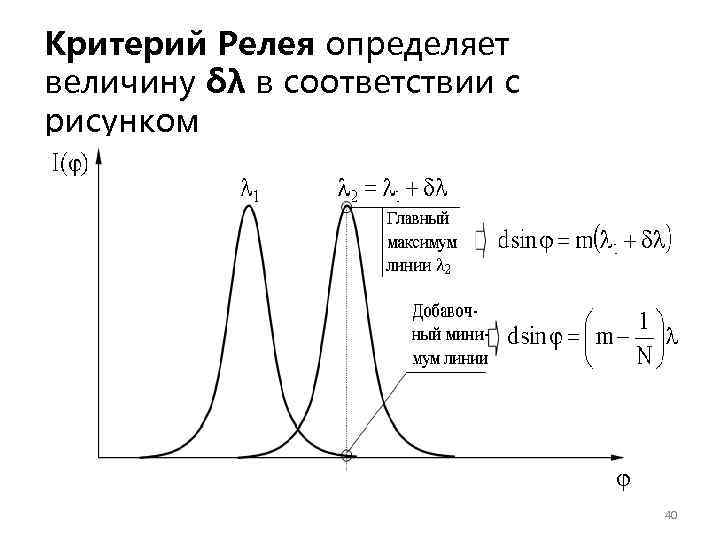Критерий Релея определяет величину δλ в соответствии с рисунком 40

. Считают, что линии разрешены, если главный максимум линии λ 1 + δλ и добавочный минимум линии λ 1 совпадает, следовательно: По определени ю. В результате получим: 41

Разрешающая сила R есть величина, обратная относительной погрешности определения длины волны. Она показывает, во сколько раз длина волны λ больше минимально возможной абсолютной N в формуле для разрешающей силы погрешности δλ. - это число щелей, принимающих участие в образовании главного максимума порядка m. Если поперечный размер падающего на решетку пучка света ln больше длины решетки lреш, то N = lреш/d, где d - 42

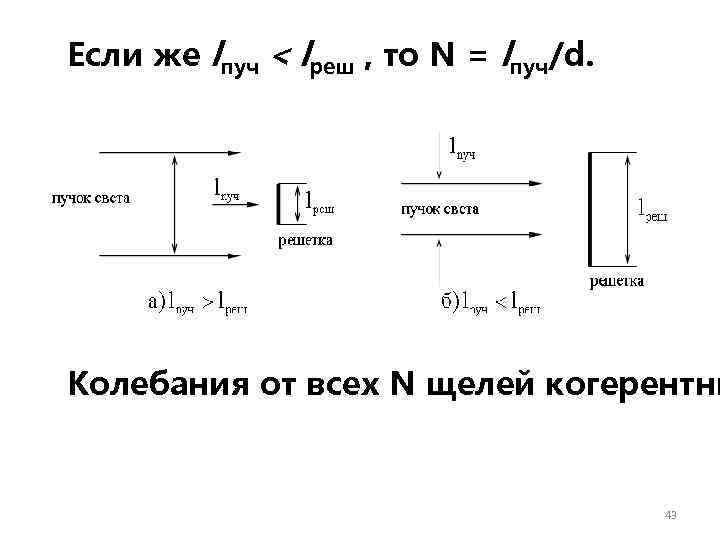Если же lпуч < lреш , то N = lпуч/d. Колебания от всех N щелей когерентны 43

При постоянном угле падения угол отклонения немонохроматического луча зависит от длины волны: = ( ). Величина d /d =(d /dn)(dn/d ), соответствующая постоянному углу падения i 1, называется угловой дисперсией. Значение dn/d определяется дифференцированием n=n 0+c/( - 0). Дисперсия показателя преломления dn/d быстро увеличивается с 44

, Линейной дисперсией называется величина dl/d. Она определяет линейное расстояние в фокальной плоскости прибора, приходящееся на единичный спектральный интервал, и измеряется в мм/нм. Линейная дисперсия связана с угловой соотношением: где f - фокусное расстояние выходного объектива прибора. Или 45

Дисперсия спектральных аппаратов имеет различное значение в разных участках спектра. Поэтому угловое и линейное расстояния между спектральными линиями, отличающимися по длине волны на одну и ту же величину, будут также различными в разных участках спектра. 46

Контрольные вопросы 1. Определение дифракции. Принцип Гюйгенса-Френеля 2. Зоны Френеля. Дифракция на круглом диске и на круглом отверстии 3. Дифракционная решетка. Главные максимумы и минимумы, дополнительные минимумы 4. Дифракция на кристаллической решетке 5. Разрешающая сила 47