ДИФРАКЦИЯ 1 Принцип Гюйгенса-Френеля Гюйгенс утверждал Каждая

ДИФРАКЦИЯ

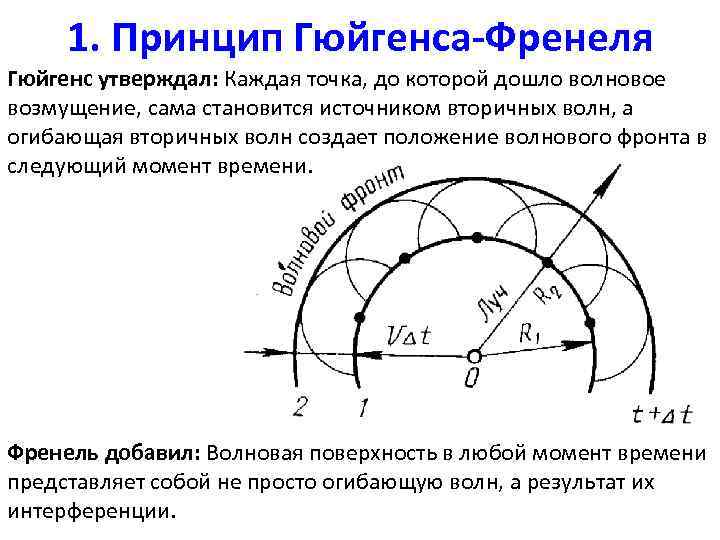1. Принцип Гюйгенса-Френеля Гюйгенс утверждал: Каждая точка, до которой дошло волновое возмущение, сама становится источником вторичных волн, а огибающая вторичных волн создает положение волнового фронта в следующий момент времени. Френель добавил: Волновая поверхность в любой момент времени представляет собой не просто огибающую волн, а результат их интерференции.

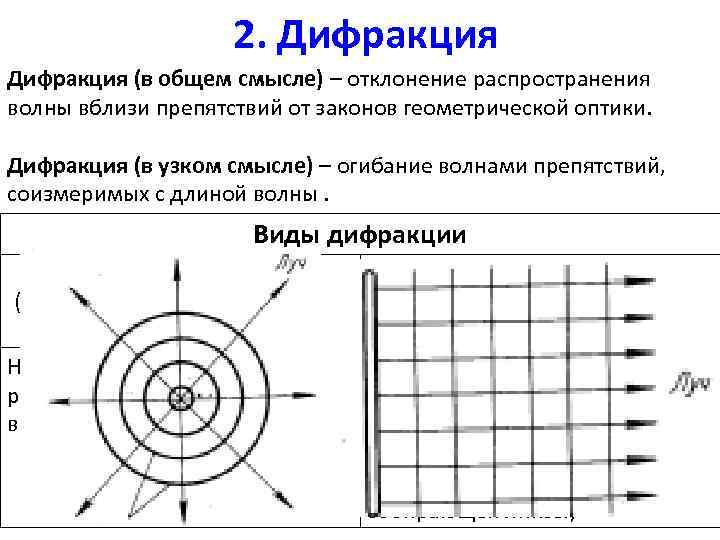2. Дифракция (в общем смысле) – отклонение распространения волны вблизи препятствий от законов геометрической оптики. Дифракция (в узком смысле) – огибание волнами препятствий, соизмеримых с длиной волны. Виды дифракции Дифракция Френеля (дифракция в сходящихся лучах, дифракция сферических волн) Наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию Дифракция Фраунгофера (дифракция в параллельных лучах, дифракция плоских волн) Наблюдается при бесконечном удалении от препятствия источника света и точки наблюдения. (на практике источник помещают в фокусе собирающей линзы)

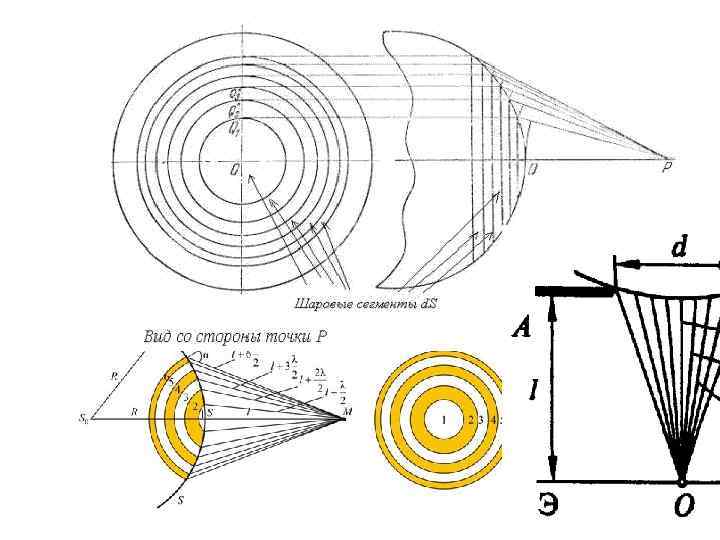
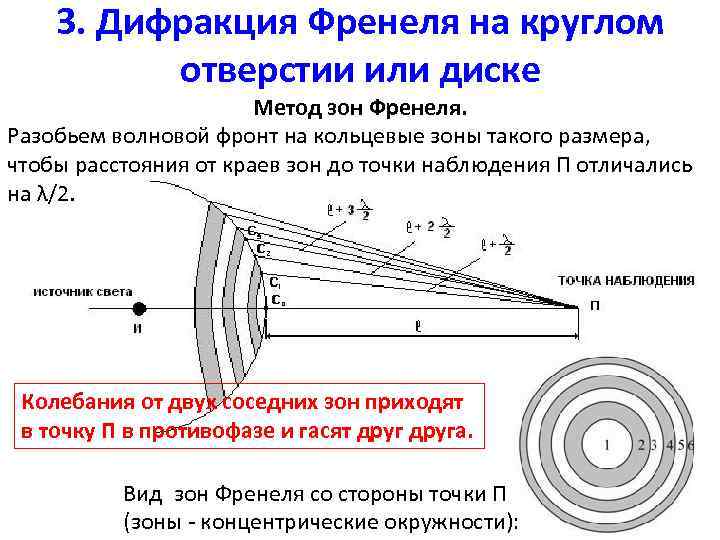3. Дифракция Френеля на круглом отверстии или диске Метод зон Френеля. Разобьем волновой фронт на кольцевые зоны такого размера, чтобы расстояния от краев зон до точки наблюдения П отличались на λ/2. Колебания от двух соседних зон приходят в точку П в противофазе и гасят друга. Вид зон Френеля со стороны точки П (зоны - концентрические окружности):

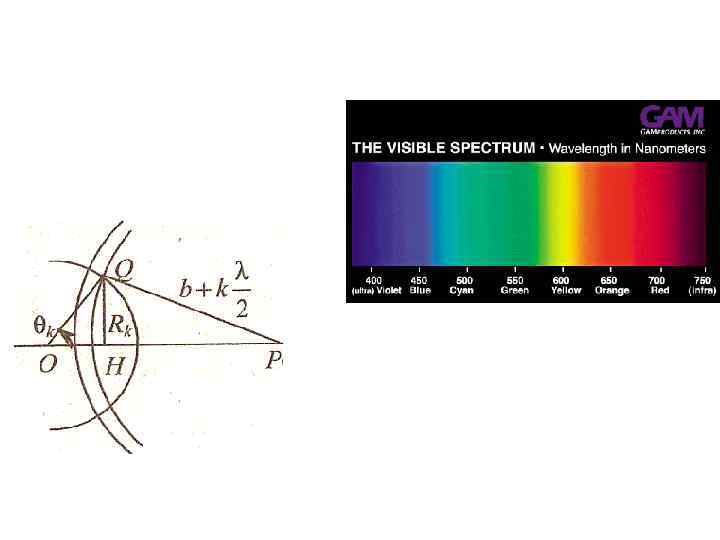
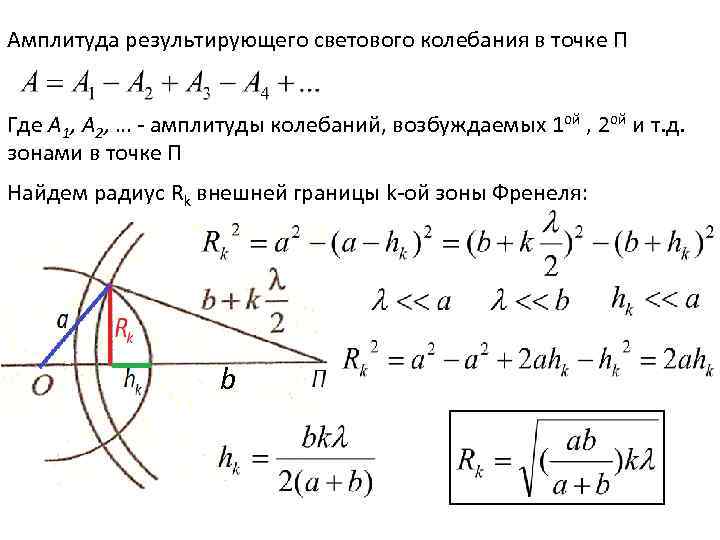Амплитуда результирующего светового колебания в точке П Где А 1, А 2, … - амплитуды колебаний, возбуждаемых 1 ой , 2 ой и т. д. зонами в точке П Найдем радиус Rk внешней границы k-ой зоны Френеля: b

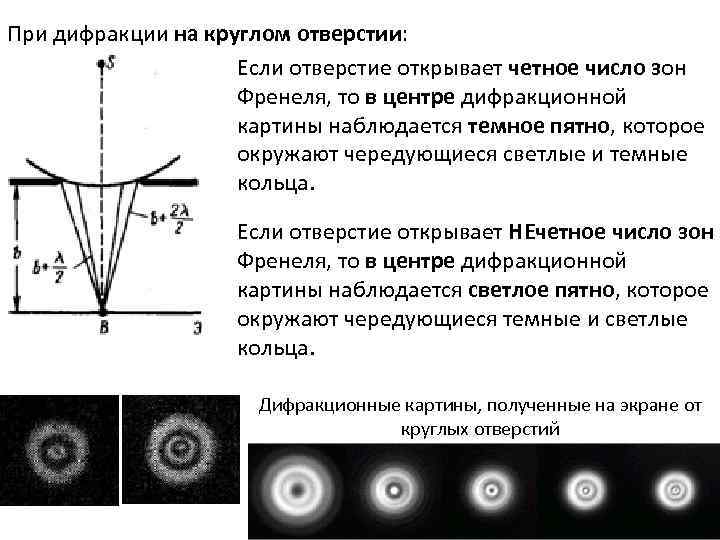При дифракции на круглом отверстии: Если отверстие открывает четное число зон Френеля, то в центре дифракционной картины наблюдается темное пятно, которое окружают чередующиеся светлые и темные кольца. Если отверстие открывает НЕчетное число зон Френеля, то в центре дифракционной картины наблюдается светлое пятно, которое окружают чередующиеся темные и светлые кольца. Дифракционные картины, полученные на экране от круглых отверстий

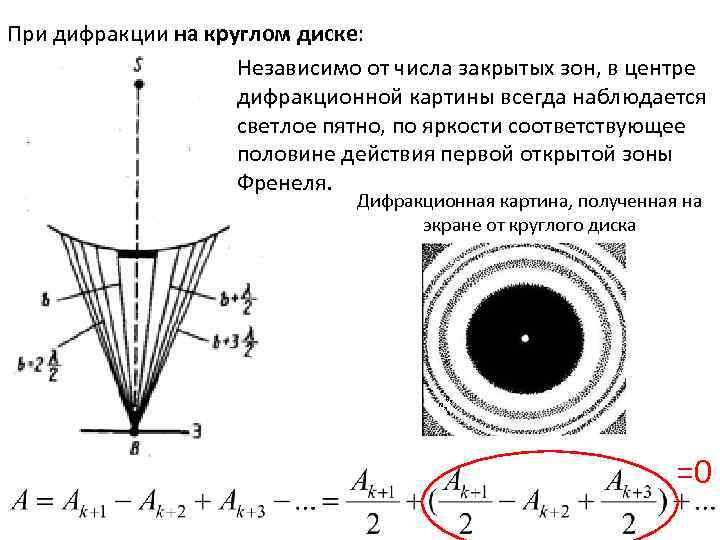При дифракции на круглом диске: Независимо от числа закрытых зон, в центре дифракционной картины всегда наблюдается светлое пятно, по яркости соответствующее половине действия первой открытой зоны Френеля. Дифракционная картина, полученная на экране от круглого диска =0

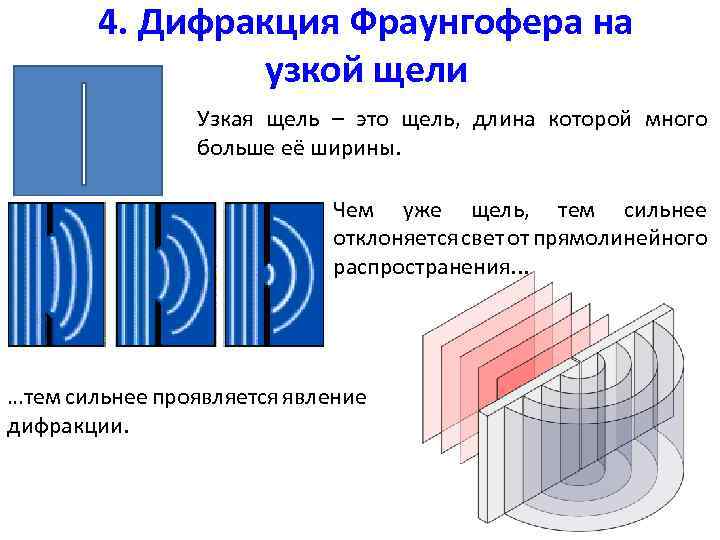4. Дифракция Фраунгофера на узкой щели Узкая щель – это щель, длина которой много больше её ширины. Чем уже щель, тем сильнее отклоняется свет от прямолинейного распространения. . . …тем сильнее проявляется явление дифракции.

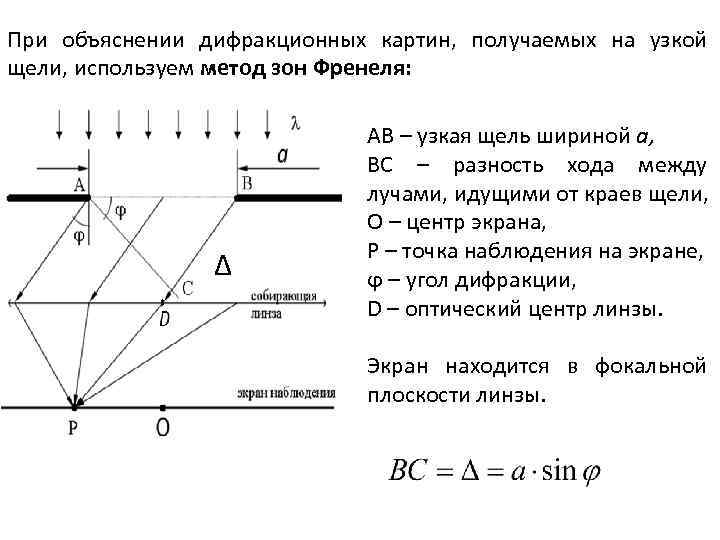При объяснении дифракционных картин, получаемых на узкой щели, используем метод зон Френеля: Δ АВ – узкая щель шириной а, ВС – разность хода между лучами, идущими от краев щели, О – центр экрана, Р – точка наблюдения на экране, ϕ – угол дифракции, D – оптический центр линзы. Экран находится в фокальной плоскости линзы.

Разобьем щель на m равных зон, где m = Δ/(λ/2), имеющих вид полос , параллельных ребру щели. При этом колебания двух соседних зон будут приходить в точку Р в противофазе и погасят друга. Если число зон четное, то в точке Р наблюдается дифракционный минимум: -условие дифракционных минимумов на узкой щели, где m = 1, 2, 3, … Если число зон НЕчетное, то в точке Р наблюдается дифракционный максимум: -условие дифракционных максимумов на узкой щели, где m = 1, 2, 3, … В центре экрана в точке О всегда наблюдается дифракционный максимум.

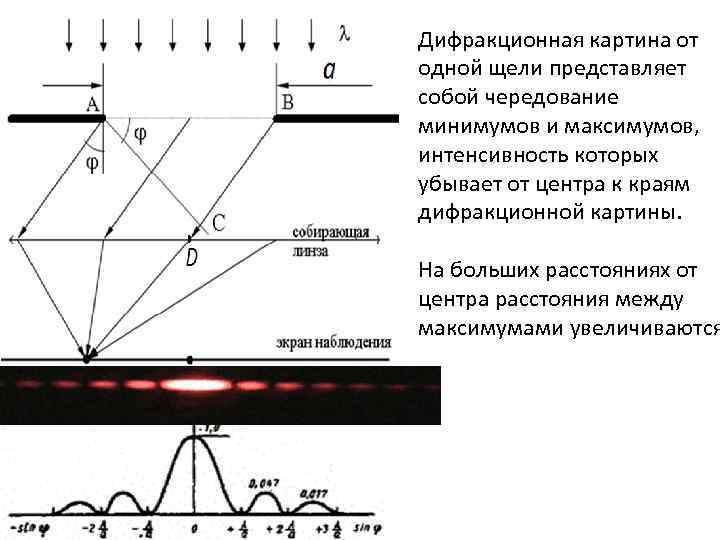Дифракционная картина от одной щели представляет собой чередование минимумов и максимумов, интенсивность которых убывает от центра к краям дифракционной картины. На больших расстояниях от центра расстояния между максимумами увеличиваются

Дифракция Фраунгофера на щели

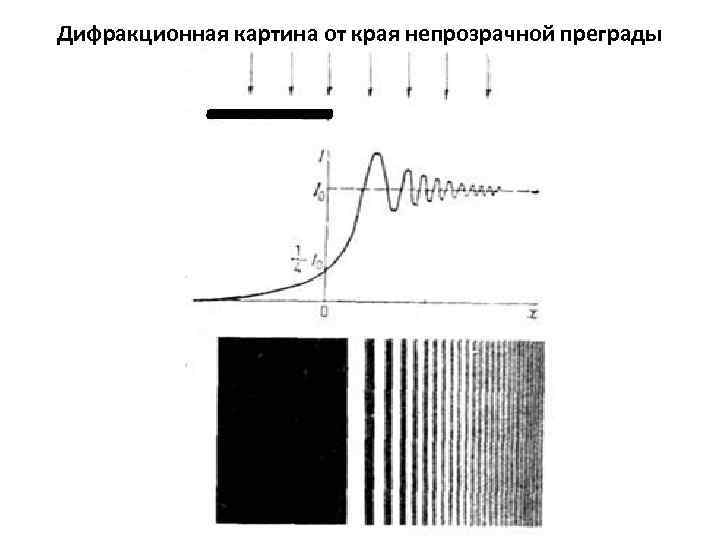Дифракционная картина от края непрозрачной преграды

Дифракция Фраунгофера на нити

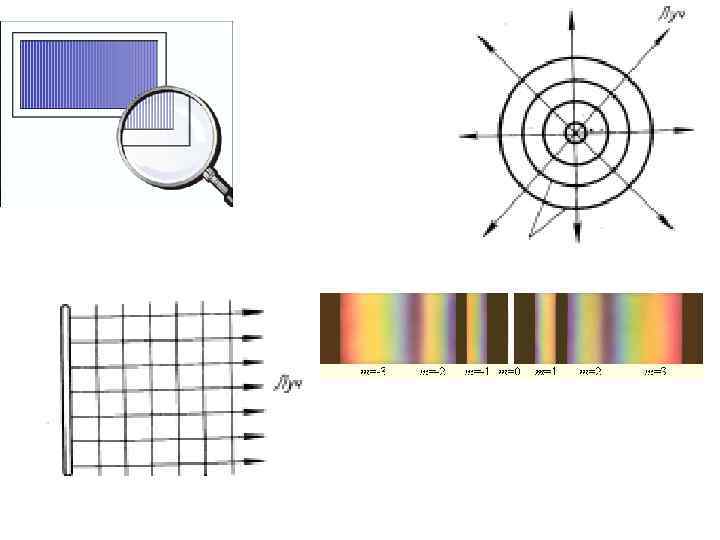
5. Дифракция Фраунгофера на дифракционной решетке Дифракционная решетка – это система параллельных щелей равной ширины, разделенных равными по ширине непрозрачными промежутками. Дифракционная картина на решетке – это результат взаимной интерференции волн, идущих от каждой из щелей. d – период дифракционной решетки (постоянная решетки) – это расстояние между краями двух соседних щелей. d = a + b, где а – ширина щели, b – ширина непрозрачного промежутка.

Разность хода лучей, идущих от двух соседних щелей: Условие главных максимумов дифракционной решетки (в этих направлениях волны усиливают друга за счет интерференции): Условие главных минимумов дифракционной решетки: Условие дополнительных минимумов дифракционной решетки (в этих направлениях волны гасят друга за счет интерференции):

Так как , то - Максимальный порядок спектра дифракционной решетки При пропускании через решетку монохроматического света в центре экрана наблюдается самый яркий максимум нулевого порядка (k = 0). Остальные максимумы тусклее и расположены симметрично по обе стороны от центрального. При пропускании через решетку белого света в центре экрана наблюдается максимум нулевого порядка (k = 0) белого цвета, так как выполняется условие максимумов для всех длин волн. Остальные максимумы разлагаются в радужный спектр. Чем больше порядок максимума, тем он шире. Дифракционная решетка используется как устройство для получения спектров.

Дифракционные решетки

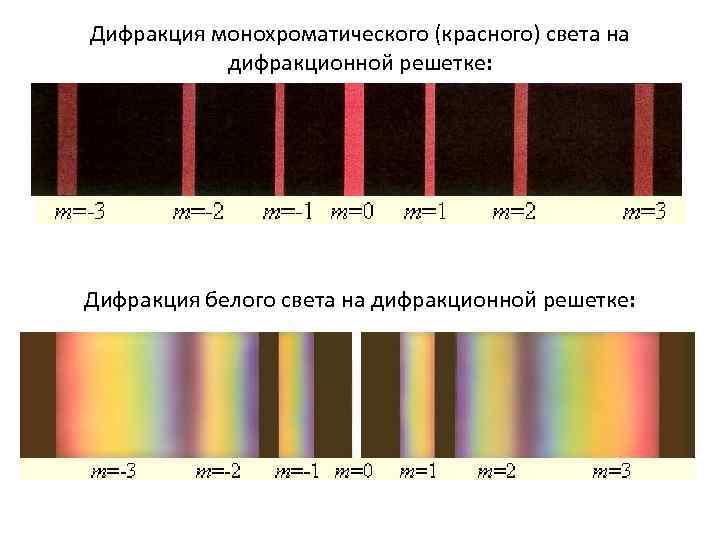Дифракция монохроматического (красного) света на дифракционной решетке: Дифракция белого света на дифракционной решетке:

Дифракция белого света

Применение дифракционных решеток для спектрального анализа: - в химии (для получения химического состава вещества); - в астрофизике (для изучения химического состава звезд ); - в металлургии (для изучения состава сплавов). - Спектр паров ртути Лаборатория спектрального анализа

спектры испускания: - Линейчатый спектр водорода - Линейчатый спектр натрия - Линейчатый спектр меди - Линейчатый спектр углерода - Полосатый спектр молекулы йода - Сплошной спектр твердого тела - Спектр поглощения солнечной атмосферы

ДИСПЕРСИЯ

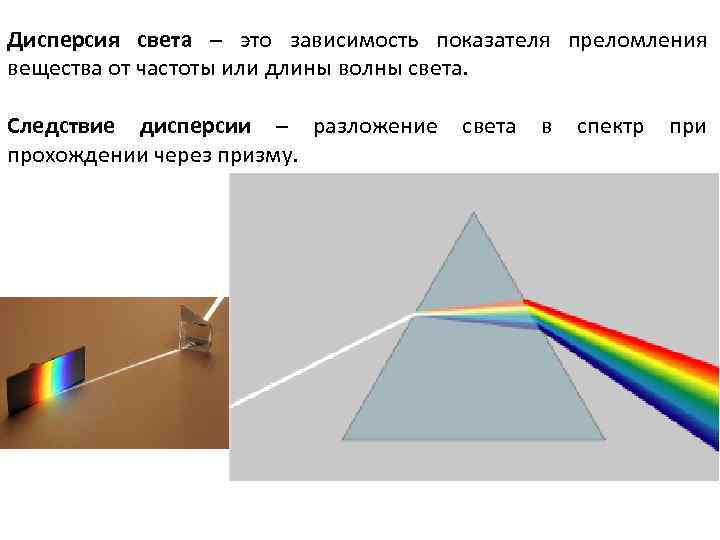Дисперсия света – это зависимость показателя преломления вещества от частоты или длины волны света. Следствие дисперсии – разложение прохождении через призму. света в спектр при

Дисперсия на призме

D – дисперсия, [м-1] – величина дисперсии показывает насколько быстро меняется показатель преломления n при изменении длины волны λ – нормальная дисперсия (для прозрачных веществ) – аномальная дисперсия

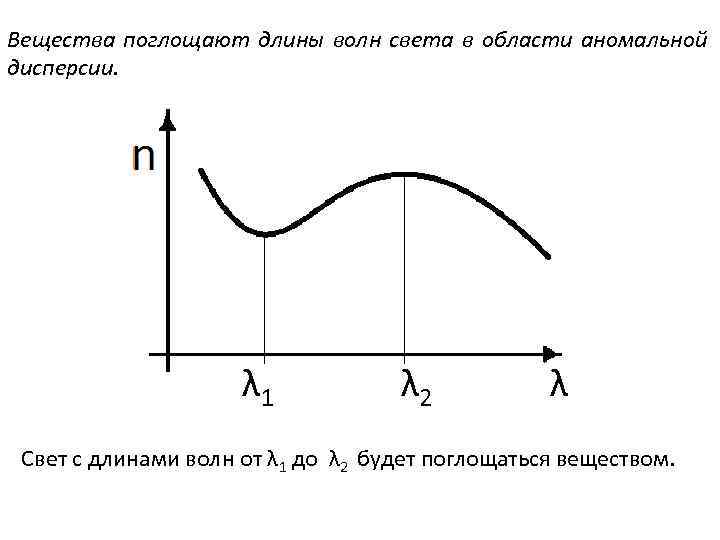Вещества поглощают длины волн света в области аномальной дисперсии. λ 1 λ 2 λ Свет с длинами волн от λ 1 до λ 2 будет поглощаться веществом.

Как появляется радуга? Радуга - есть большой изогнутый дисперсионный спектр, образовавшийся в результате разложения луча света, проходящего через капельки дождя. В данном случае капли дождя выполняют роль призмы. Радуга появляется только в то время, когда идет дождь и одновременно светит солнце. Находиться необходимо строго между солнцем (оно должно быть сзади) и дождем (он должен быть перед тобой). Иначе радуги не увидеть!

Отличие дифракционного спектра от дисперсионного 1. При дифракции сильнее отклоняются от первоначального направления распространения длинные волны (красный край спектра), а при дисперсии – короткие волны (фиолетовый край спектра). 2. При дифракции сильнее растянут красный край спектра, а при дисперсии – фиолетовый. 3. При дифракции изменение направления светового луча происходит линейно относительно длины волны, а при дисперсии – нелинейно. 4. Дифракционный спектр состоит из отдельных тонких линий, дисперсионный спектр – сплошной.