acd27d5f44cb5d2fe8ba2613da5a8cd3.ppt
- Количество слайдов: 70
 Diffraction 1
Diffraction 1
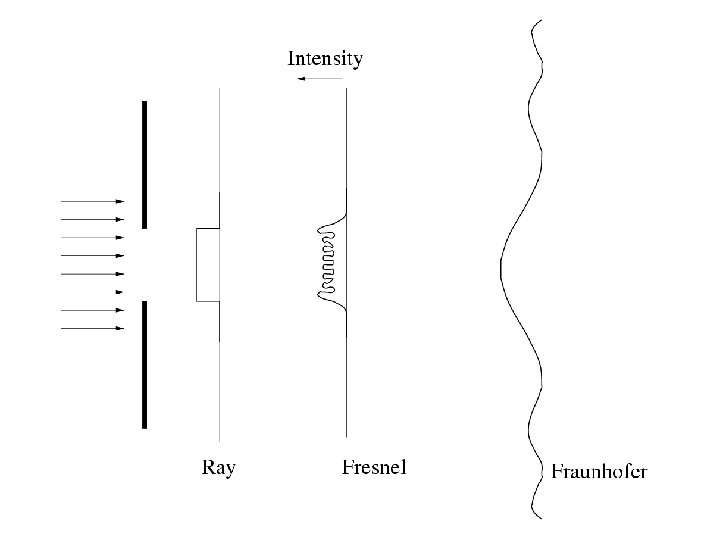
 Diffraction “Any deviation of light rays from rectilinear path which is neither reflection nor refraction is known as diffraction. ” (Sommerfeld) Types or kinds of diffraction: 1. Fraunhofer (1787 -1826) 2. Fresnel (1788 -1827)
Diffraction “Any deviation of light rays from rectilinear path which is neither reflection nor refraction is known as diffraction. ” (Sommerfeld) Types or kinds of diffraction: 1. Fraunhofer (1787 -1826) 2. Fresnel (1788 -1827)
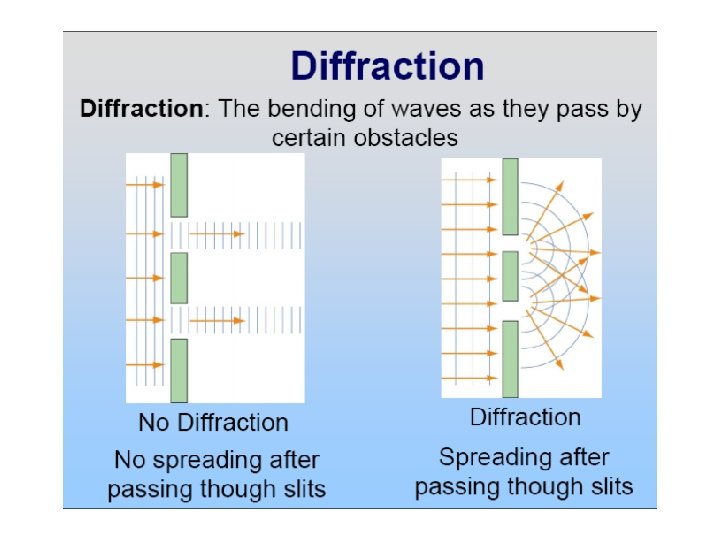
 • In addition to interference, waves also exhibit another property – diffraction. • It is the bending of the waves as they pass by some objects or through an aperture. • The phenomenon of diffraction can be understood using Huygen’s principle
• In addition to interference, waves also exhibit another property – diffraction. • It is the bending of the waves as they pass by some objects or through an aperture. • The phenomenon of diffraction can be understood using Huygen’s principle
 Diffraction of ocean water waves Ocean waves passing through slits in Tel Aviv, Israel Diffraction occurs for all waves, whatever the phenomenon.
Diffraction of ocean water waves Ocean waves passing through slits in Tel Aviv, Israel Diffraction occurs for all waves, whatever the phenomenon.
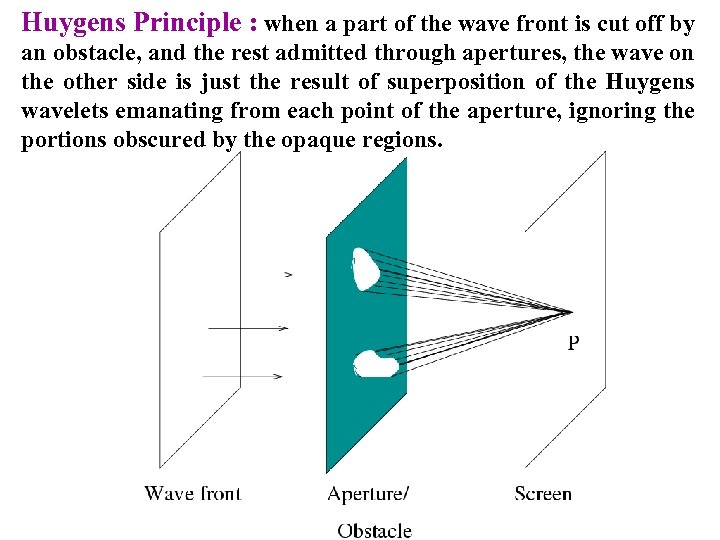 Huygens Principle : when a part of the wave front is cut off by an obstacle, and the rest admitted through apertures, the wave on the other side is just the result of superposition of the Huygens wavelets emanating from each point of the aperture, ignoring the portions obscured by the opaque regions.
Huygens Principle : when a part of the wave front is cut off by an obstacle, and the rest admitted through apertures, the wave on the other side is just the result of superposition of the Huygens wavelets emanating from each point of the aperture, ignoring the portions obscured by the opaque regions.
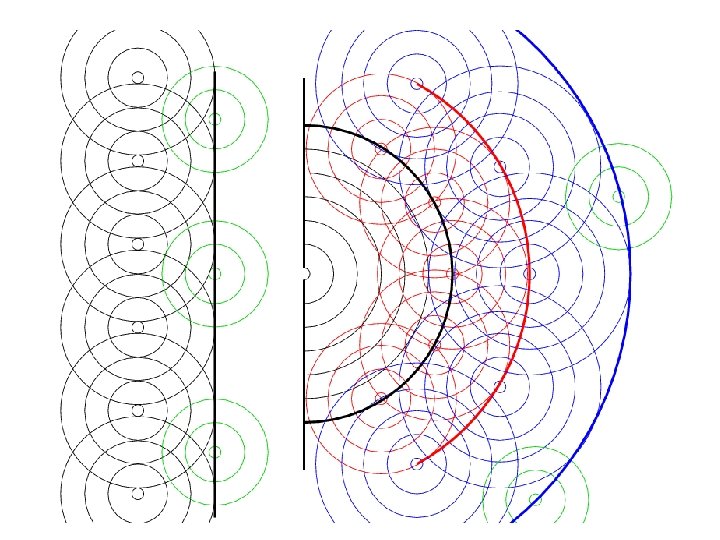
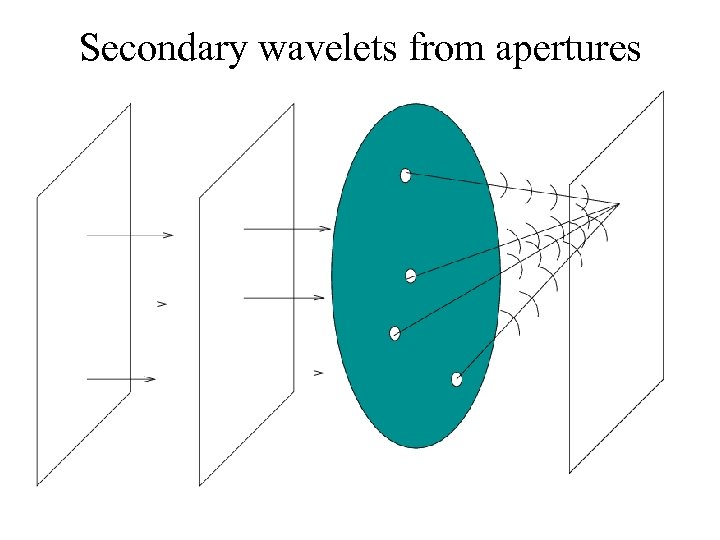 Secondary wavelets from apertures
Secondary wavelets from apertures
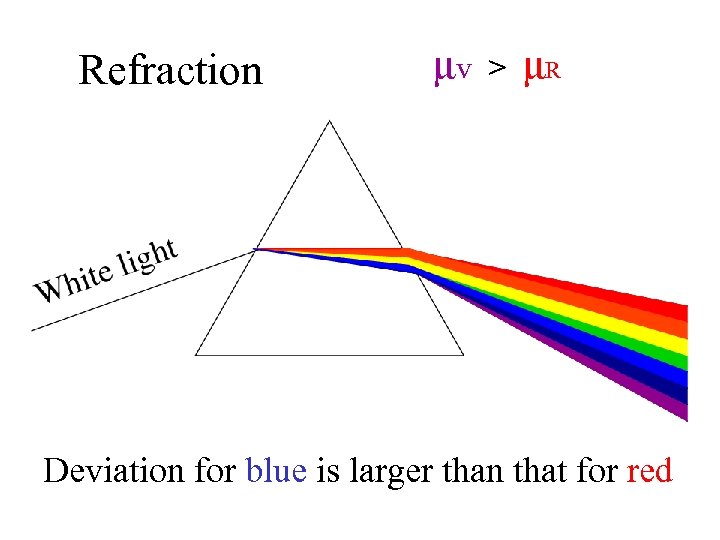 Refraction μv > μR Deviation for blue is larger than that for red
Refraction μv > μR Deviation for blue is larger than that for red
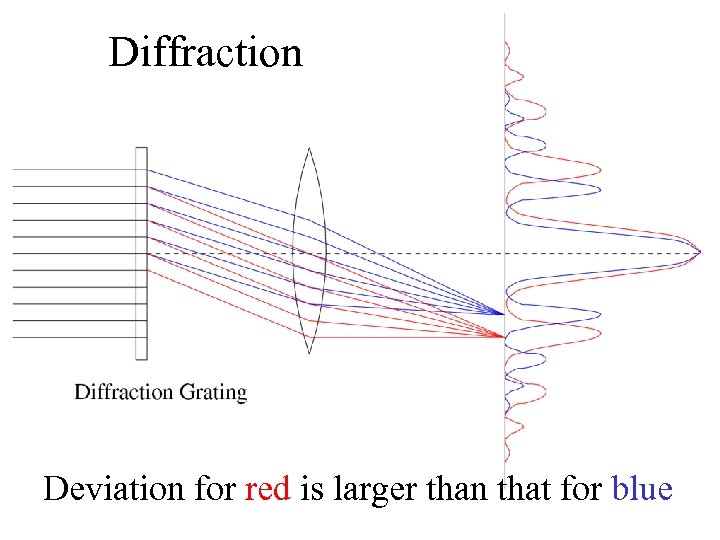 Diffraction Deviation for red is larger than that for blue
Diffraction Deviation for red is larger than that for blue
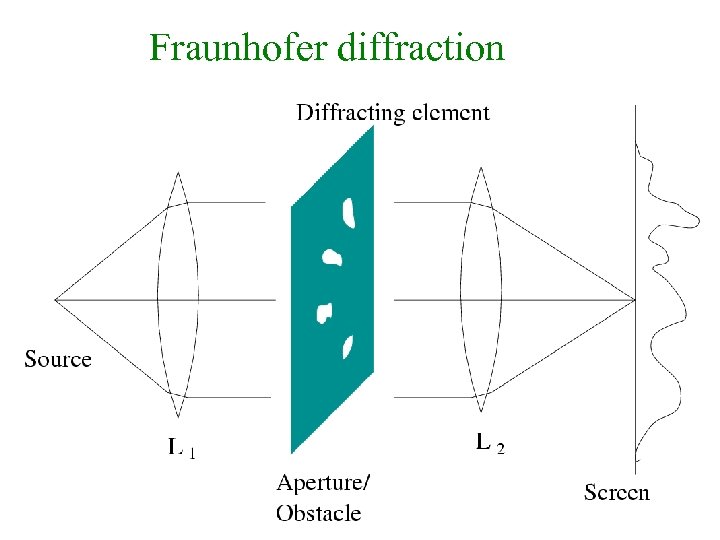 Fraunhofer diffraction
Fraunhofer diffraction
 Single slit diffraction Principal maximum
Single slit diffraction Principal maximum
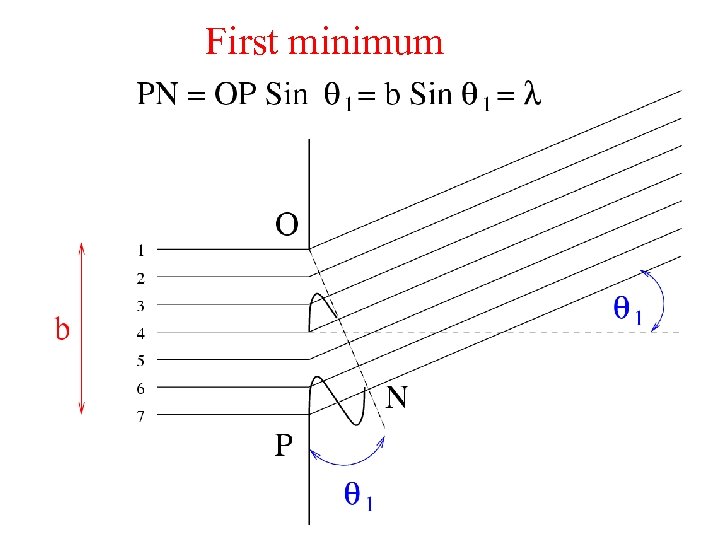 First minimum
First minimum
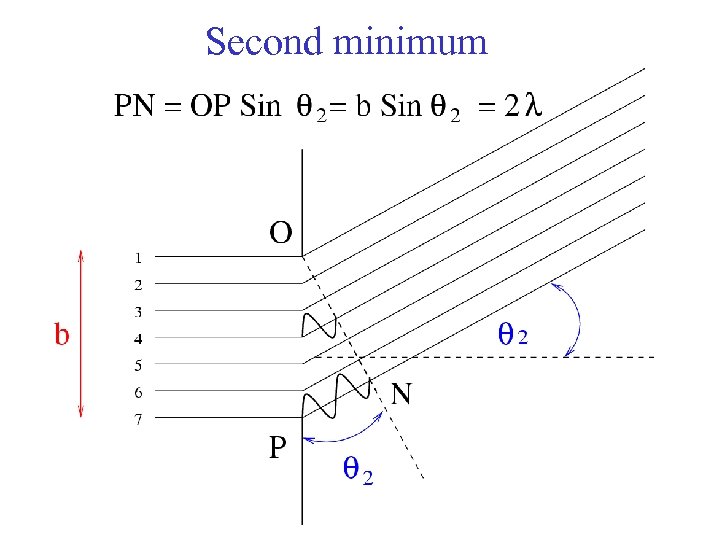 Second minimum
Second minimum
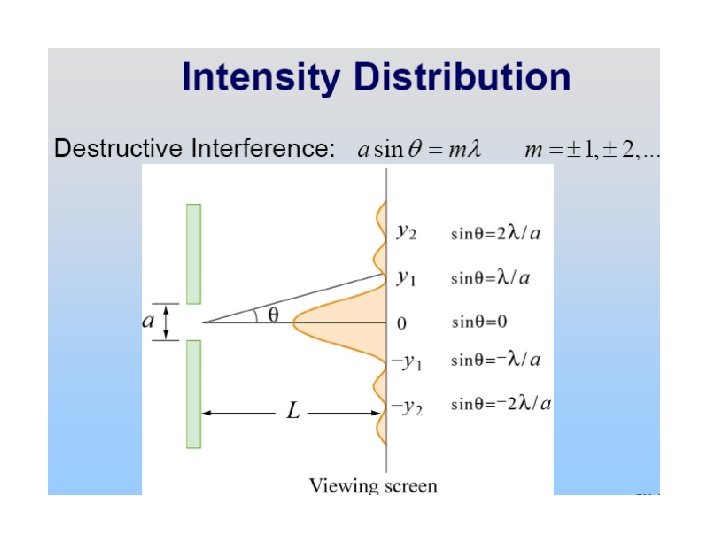
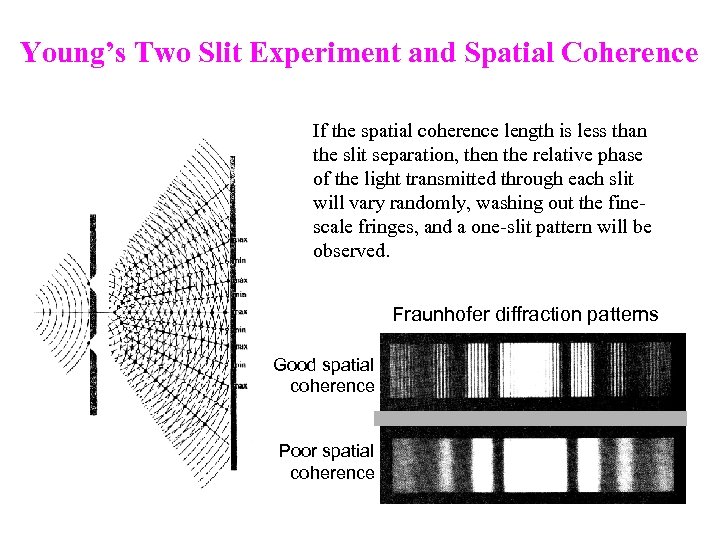 Young’s Two Slit Experiment and Spatial Coherence If the spatial coherence length is less than the slit separation, then the relative phase of the light transmitted through each slit will vary randomly, washing out the finescale fringes, and a one-slit pattern will be observed. Fraunhofer diffraction patterns Good spatial coherence Poor spatial coherence
Young’s Two Slit Experiment and Spatial Coherence If the spatial coherence length is less than the slit separation, then the relative phase of the light transmitted through each slit will vary randomly, washing out the finescale fringes, and a one-slit pattern will be observed. Fraunhofer diffraction patterns Good spatial coherence Poor spatial coherence
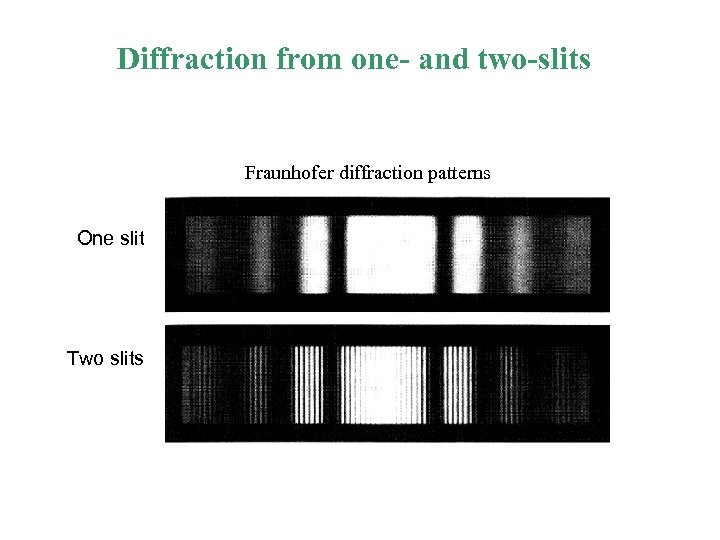 Diffraction from one- and two-slits Fraunhofer diffraction patterns One slit Two slits
Diffraction from one- and two-slits Fraunhofer diffraction patterns One slit Two slits
 Diffraction from small and large circular apertures Far-field intensity pattern from a small aperture Far-field intensity pattern from a large aperture
Diffraction from small and large circular apertures Far-field intensity pattern from a small aperture Far-field intensity pattern from a large aperture
 Diffraction from multiple slits Slit Pattern Diffraction Pattern
Diffraction from multiple slits Slit Pattern Diffraction Pattern
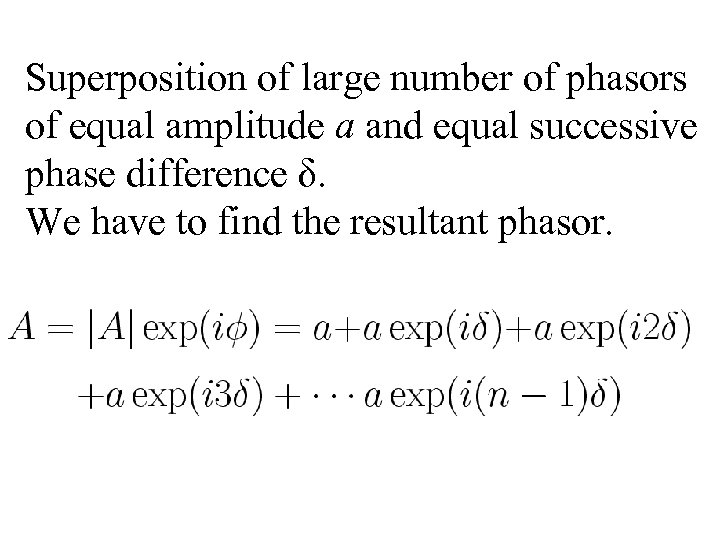 Superposition of large number of phasors of equal amplitude a and equal successive phase difference δ. We have to find the resultant phasor.
Superposition of large number of phasors of equal amplitude a and equal successive phase difference δ. We have to find the resultant phasor.
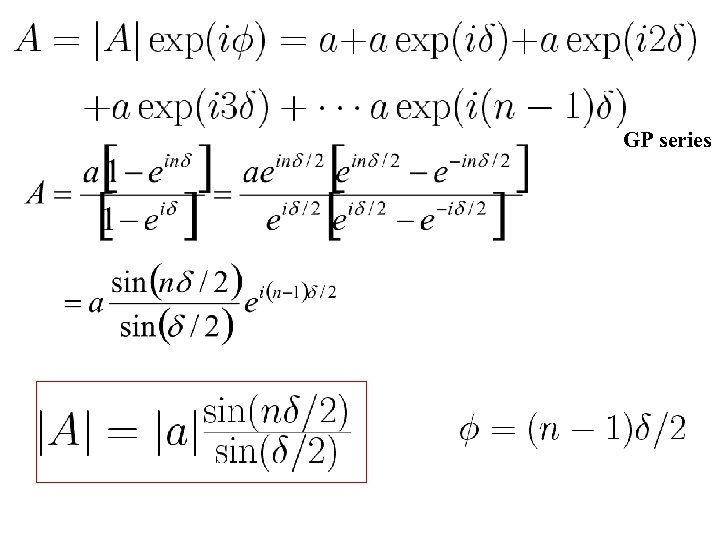 GP series
GP series
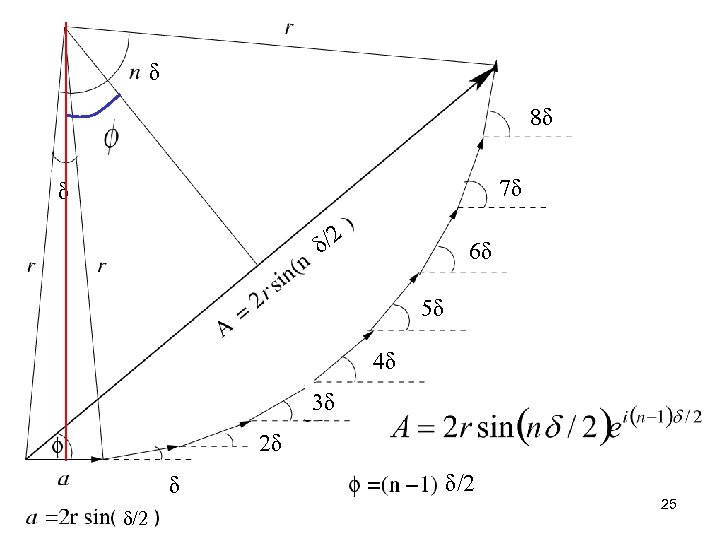 δ 8δ 7δ δ δ/2 6δ 5δ 4δ 3δ 2δ δ δ/2 25
δ 8δ 7δ δ δ/2 6δ 5δ 4δ 3δ 2δ δ δ/2 25
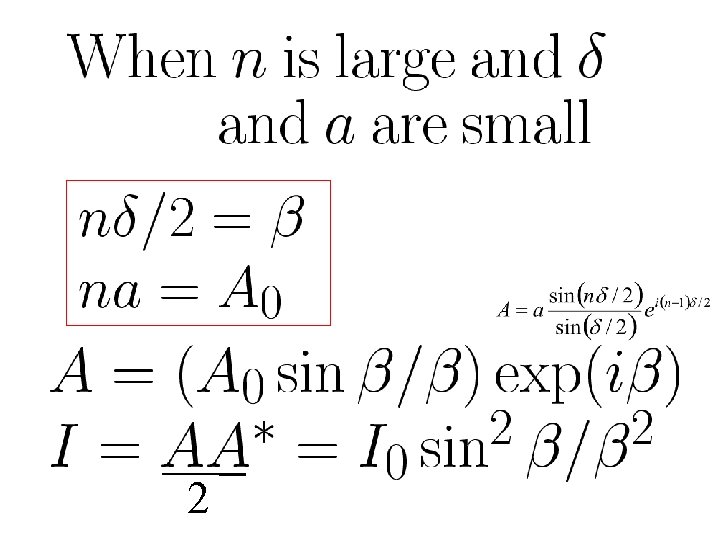 2
2
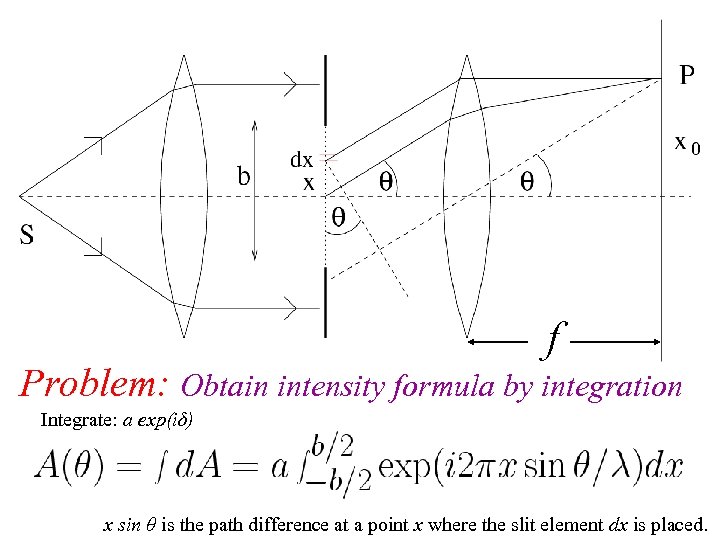 f Problem: Obtain intensity formula by integration Integrate: a exp(iδ) x sin θ is the path difference at a point x where the slit element dx is placed.
f Problem: Obtain intensity formula by integration Integrate: a exp(iδ) x sin θ is the path difference at a point x where the slit element dx is placed.
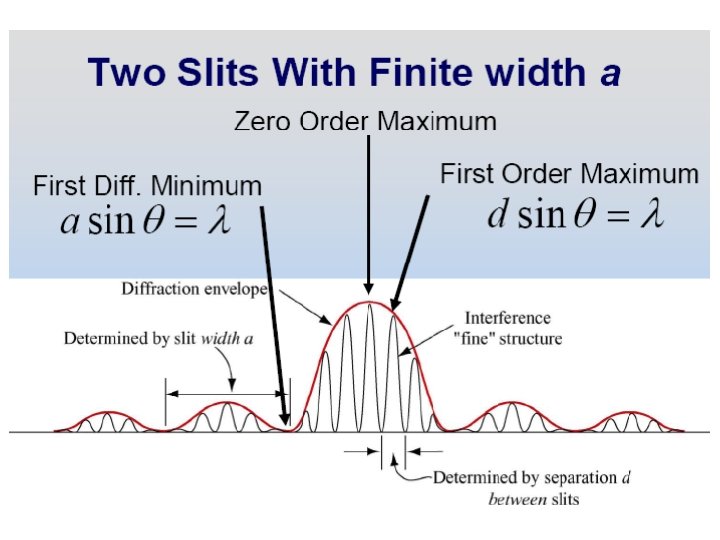
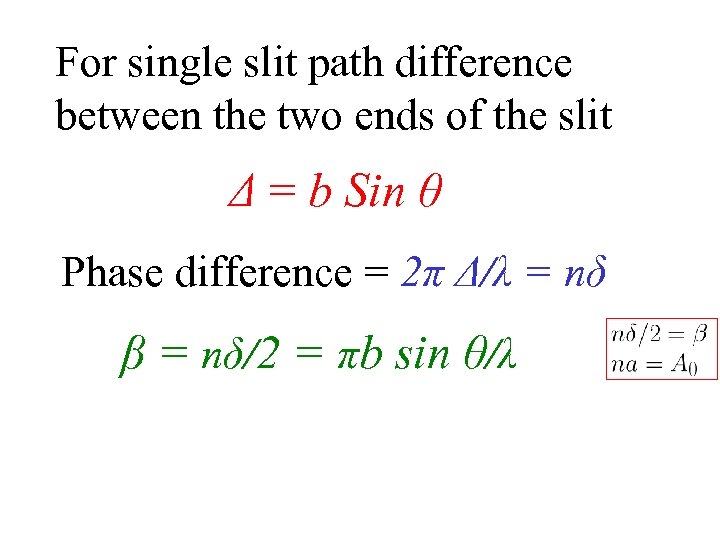 For single slit path difference between the two ends of the slit Δ = b Sin θ Phase difference = 2π Δ/λ = nδ β = nδ/2 = πb sin θ/λ
For single slit path difference between the two ends of the slit Δ = b Sin θ Phase difference = 2π Δ/λ = nδ β = nδ/2 = πb sin θ/λ
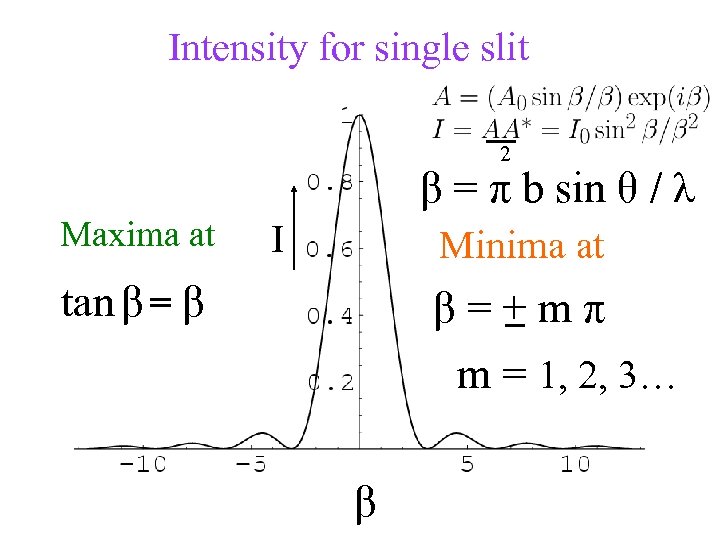 Intensity for single slit 2 β = π b sin θ / λ Maxima at I Minima at _ β=+mπ tan β = β m = 1, 2, 3… β
Intensity for single slit 2 β = π b sin θ / λ Maxima at I Minima at _ β=+mπ tan β = β m = 1, 2, 3… β
 For Principal maxima 2 β = π b Sin θ / λ
For Principal maxima 2 β = π b Sin θ / λ
 For extrema of I(q) tan β = β
For extrema of I(q) tan β = β
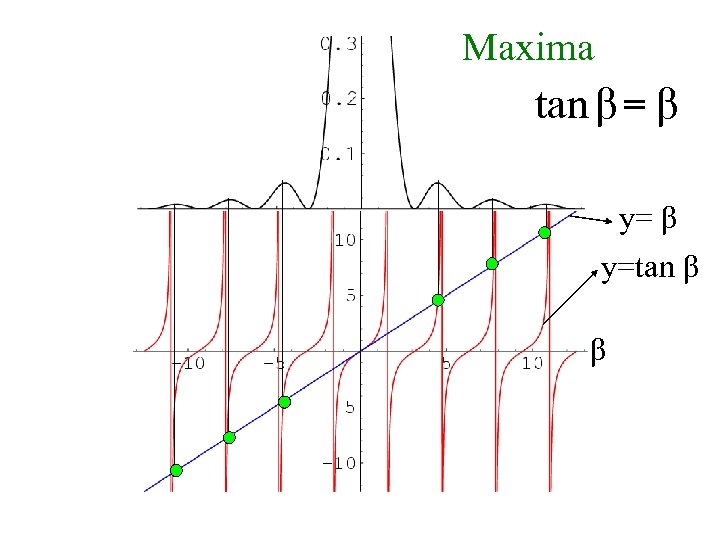 Maxima tan β = β y=tan β β
Maxima tan β = β y=tan β β
 For subsidiary maxima
For subsidiary maxima
 Full width of central maximum (First minima at sin ~ = /b) =λ/b Diffraction envelope size Δx=fλ/b 0 Δx Point source f Smearing effect of diffraction 0
Full width of central maximum (First minima at sin ~ = /b) =λ/b Diffraction envelope size Δx=fλ/b 0 Δx Point source f Smearing effect of diffraction 0
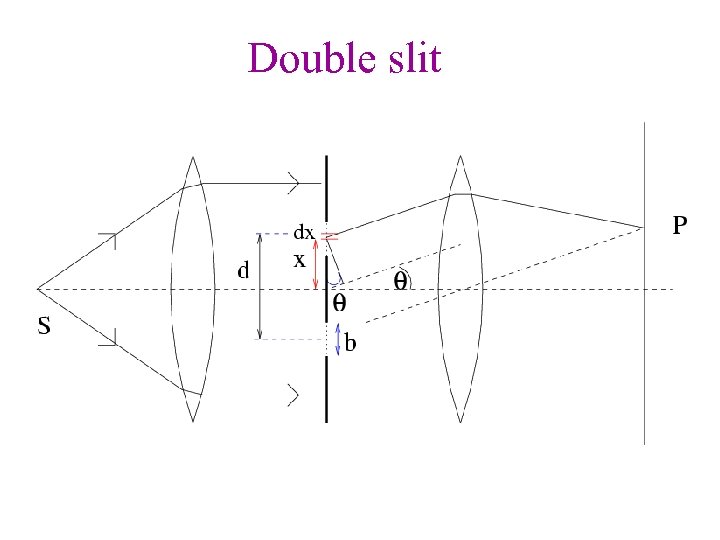 Double slit
Double slit
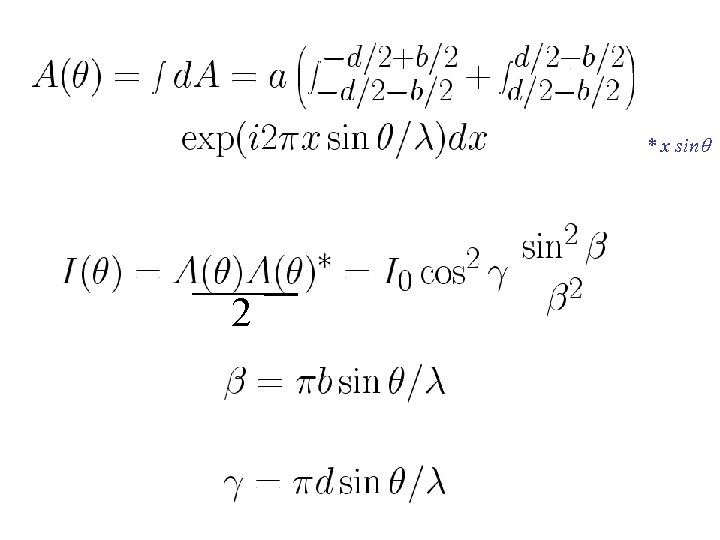 Phase=(2π/ ) * x sin 2
Phase=(2π/ ) * x sin 2
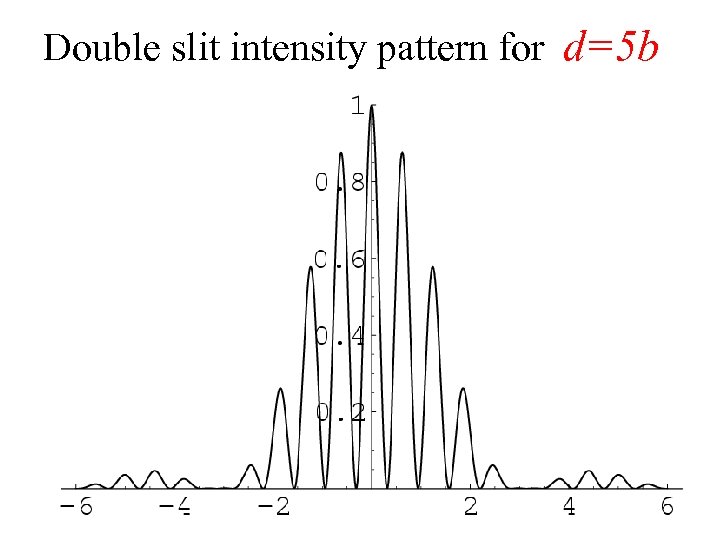 Double slit intensity pattern for d=5 b
Double slit intensity pattern for d=5 b
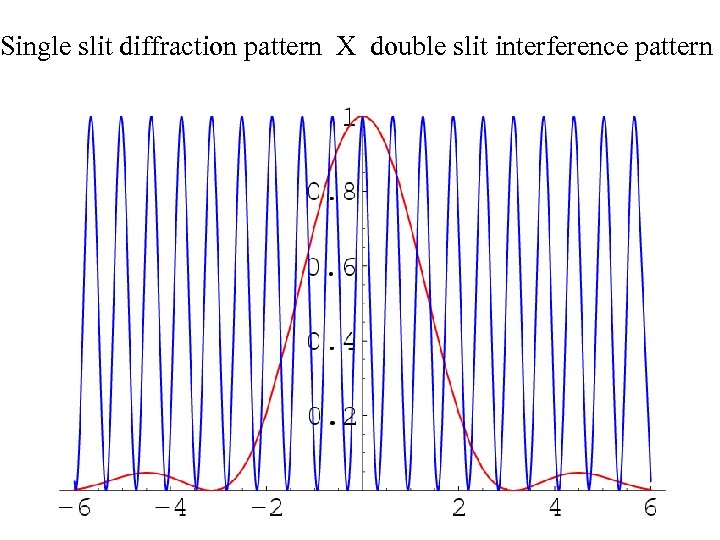 Single slit diffraction pattern X double slit interference pattern
Single slit diffraction pattern X double slit interference pattern
 Condition for Missing orders Diffraction Minima at b sin θ = m λ m=0 / Interference Maxima at d sin θ = n λ When the above two equations are satisfied at the same point in the pattern (same θ), dividing one equation by the other gives the condition for missing orders.
Condition for Missing orders Diffraction Minima at b sin θ = m λ m=0 / Interference Maxima at d sin θ = n λ When the above two equations are satisfied at the same point in the pattern (same θ), dividing one equation by the other gives the condition for missing orders.
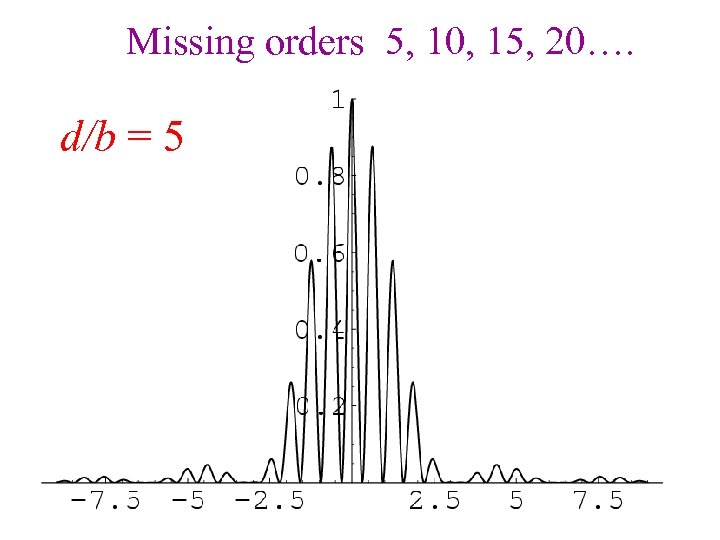 Missing orders 5, 10, 15, 20…. d/b = 5
Missing orders 5, 10, 15, 20…. d/b = 5
 When we use the double-source equation to find locations of bright spots, we find that there are some places where we expect to see bright spots, but we see no light. This is known as a missing order, and it happens because at that location there's a zero in the single slit pattern.
When we use the double-source equation to find locations of bright spots, we find that there are some places where we expect to see bright spots, but we see no light. This is known as a missing order, and it happens because at that location there's a zero in the single slit pattern.
 Remember! If the zero in the single slit pattern, and a zero in the double slit pattern coincides, it is not called a missing order, as there is no order to be missing! Also, if there is a local peak in the single slit pattern, and a zero in the double source pattern, there will still be a zero (remember, we multiply the functions!) - this is also not a missing order.
Remember! If the zero in the single slit pattern, and a zero in the double slit pattern coincides, it is not called a missing order, as there is no order to be missing! Also, if there is a local peak in the single slit pattern, and a zero in the double source pattern, there will still be a zero (remember, we multiply the functions!) - this is also not a missing order.
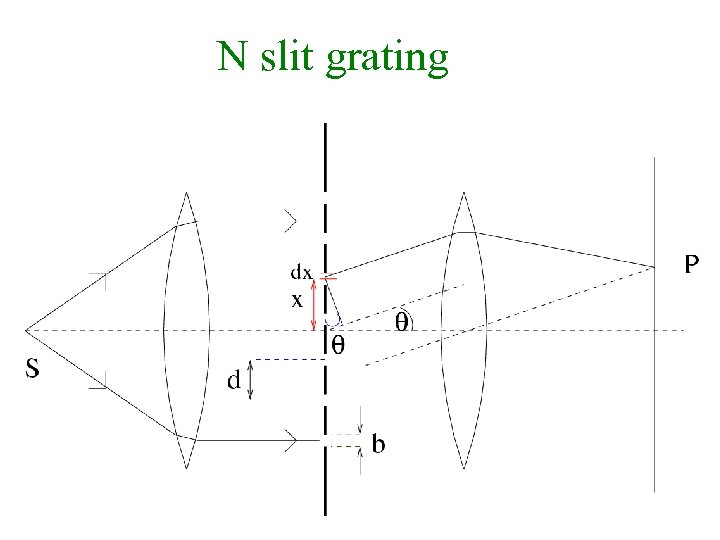 N slit grating
N slit grating
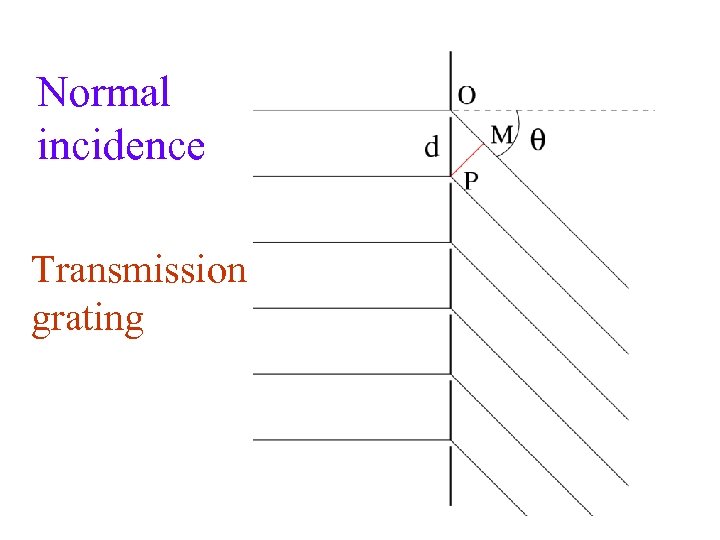 Normal incidence Transmission grating
Normal incidence Transmission grating
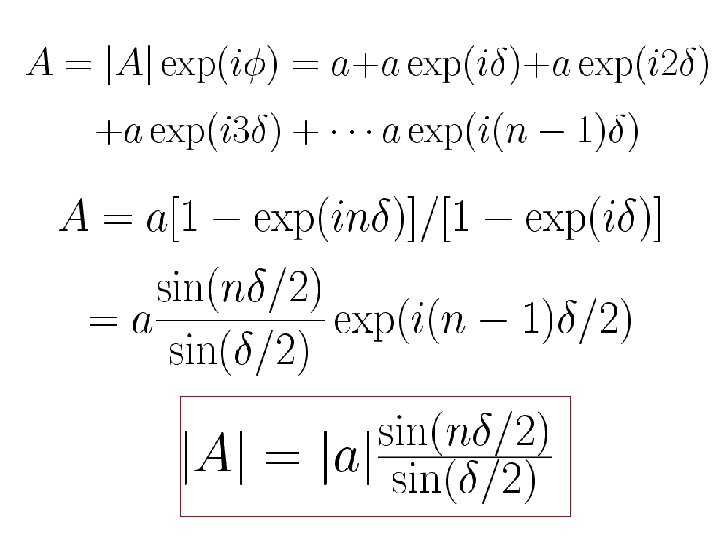
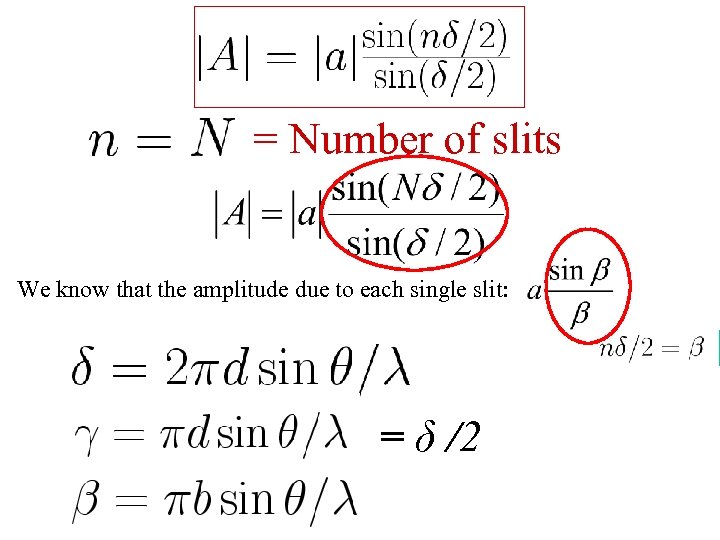 = Number of slits We know that the amplitude due to each single slit: = δ /2
= Number of slits We know that the amplitude due to each single slit: = δ /2
 Intensity pattern Diffraction Interference for small b
Intensity pattern Diffraction Interference for small b
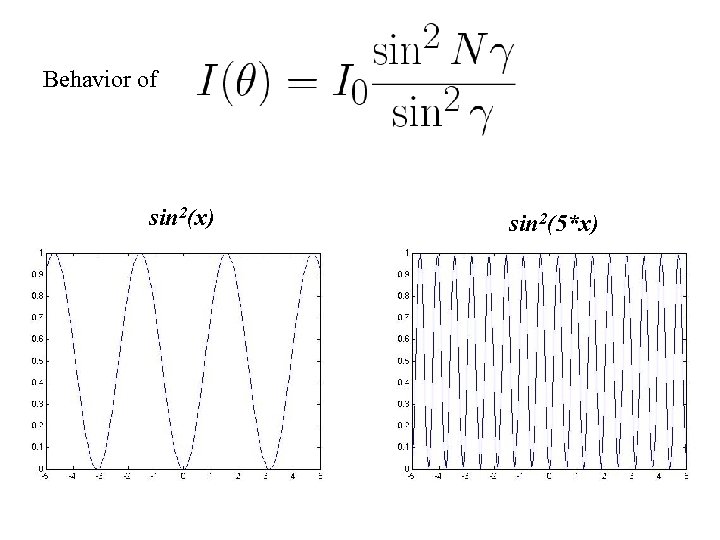 Behavior of sin 2(x) sin 2(5*x)
Behavior of sin 2(x) sin 2(5*x)
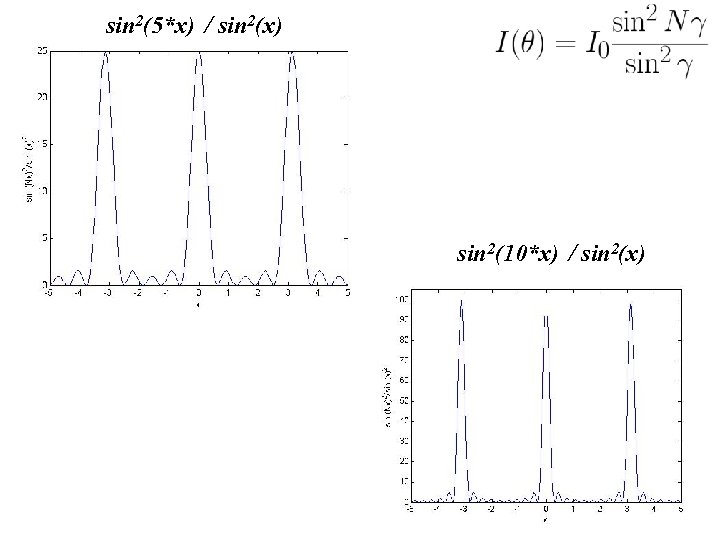 sin 2(5*x) / sin 2(x) sin 2(10*x) / sin 2(x)
sin 2(5*x) / sin 2(x) sin 2(10*x) / sin 2(x)
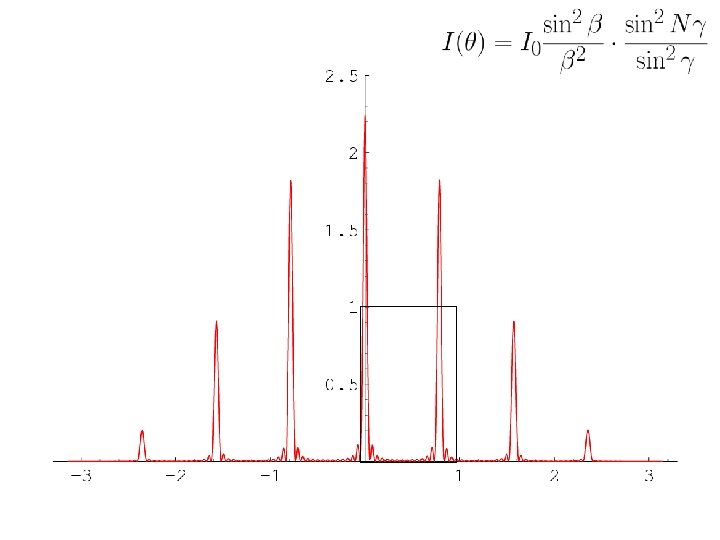
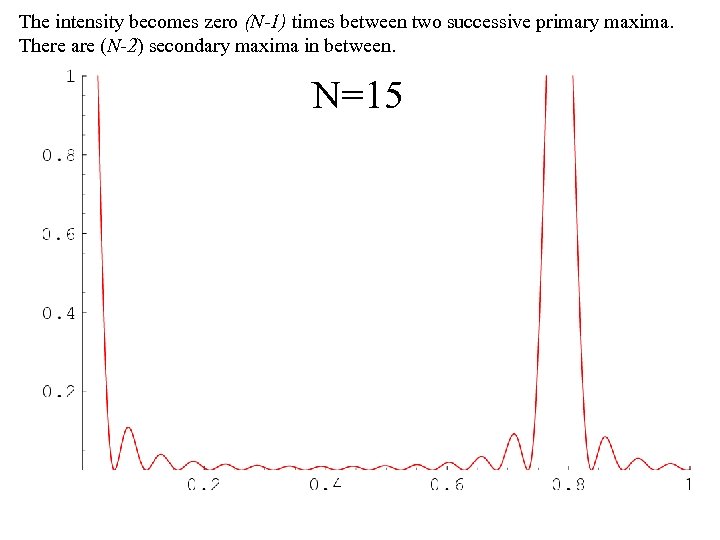
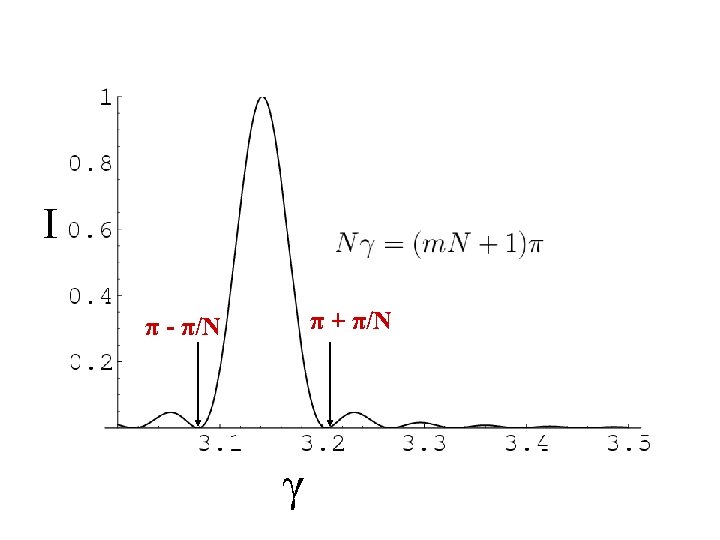
 When = 0, or mπ (m = 0, ± 1, ± 2, …) The intensity is maximum when this condition is satisfied. These are called the Primary maxima. m gives the order of the maximum. The intensity drops away from the primary maxima. The intensity becomes zero (N-1) times between two successive primary maxima. There are (N-2) secondary maxima in between. As N increases the number of secondary maxima increases and the primary maxima becomes sharper.
When = 0, or mπ (m = 0, ± 1, ± 2, …) The intensity is maximum when this condition is satisfied. These are called the Primary maxima. m gives the order of the maximum. The intensity drops away from the primary maxima. The intensity becomes zero (N-1) times between two successive primary maxima. There are (N-2) secondary maxima in between. As N increases the number of secondary maxima increases and the primary maxima becomes sharper.
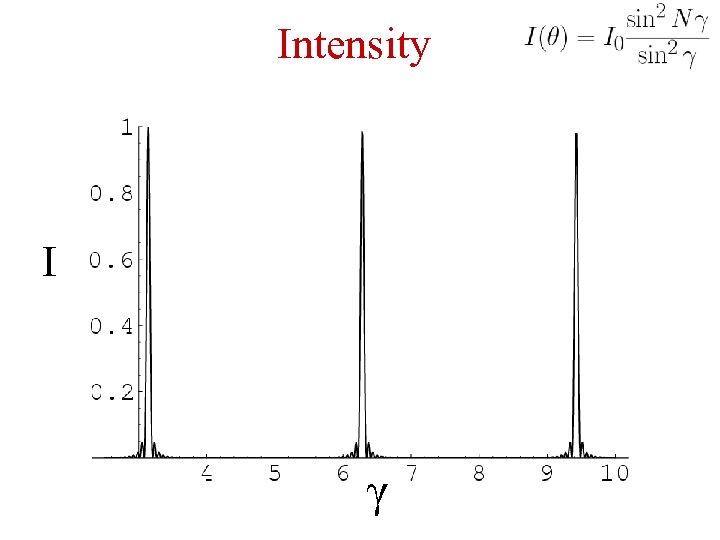 Intensity I γ
Intensity I γ
 The intensity becomes zero (N-1) times between two successive primary maxima. There are (N-2) secondary maxima in between. N=15
The intensity becomes zero (N-1) times between two successive primary maxima. There are (N-2) secondary maxima in between. N=15
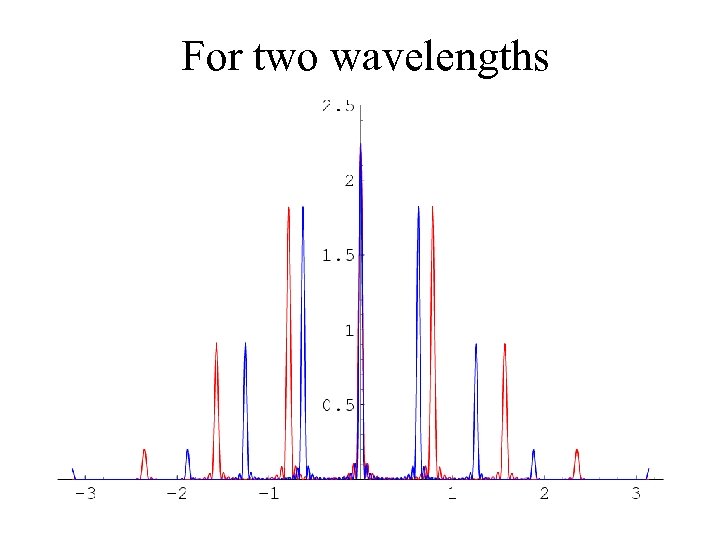 For two wavelengths
For two wavelengths
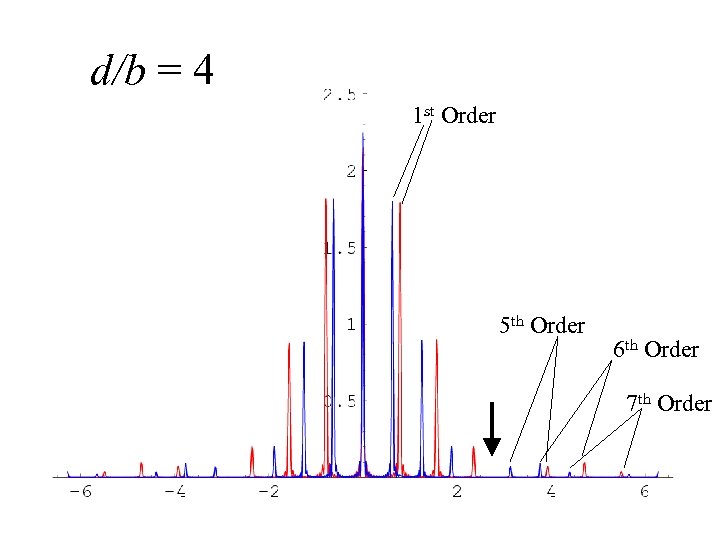 d/b = 4 1 st Order 5 th Order 6 th Order 7 th Order
d/b = 4 1 st Order 5 th Order 6 th Order 7 th Order
 Principal maxima When = 0, or mπ (m = 0, ± 1, ± 2, …) Minima Because at minima we should have, sin 0 If maximum is at m and Δ w is the width, then the intensity should be zero at ( m + Δ w )
Principal maxima When = 0, or mπ (m = 0, ± 1, ± 2, …) Minima Because at minima we should have, sin 0 If maximum is at m and Δ w is the width, then the intensity should be zero at ( m + Δ w )
 I π + π/N π - π/N γ
I π + π/N π - π/N γ
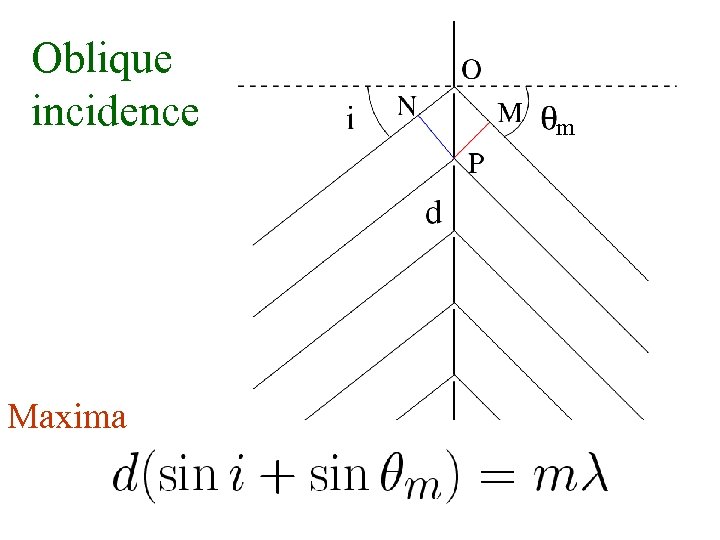 Oblique incidence Maxima m
Oblique incidence Maxima m
 Let us estimate the width of the mth order Principal maximum sin (A+B) = sin A cos B + cos A sin B d sin θm = mλ
Let us estimate the width of the mth order Principal maximum sin (A+B) = sin A cos B + cos A sin B d sin θm = mλ
 Width of principal maxima When does the principal maxima get sharper? Dispersive power of grating is defined as Differentiate:
Width of principal maxima When does the principal maxima get sharper? Dispersive power of grating is defined as Differentiate:
 Chromatic resolving power of a grating =m. N
Chromatic resolving power of a grating =m. N
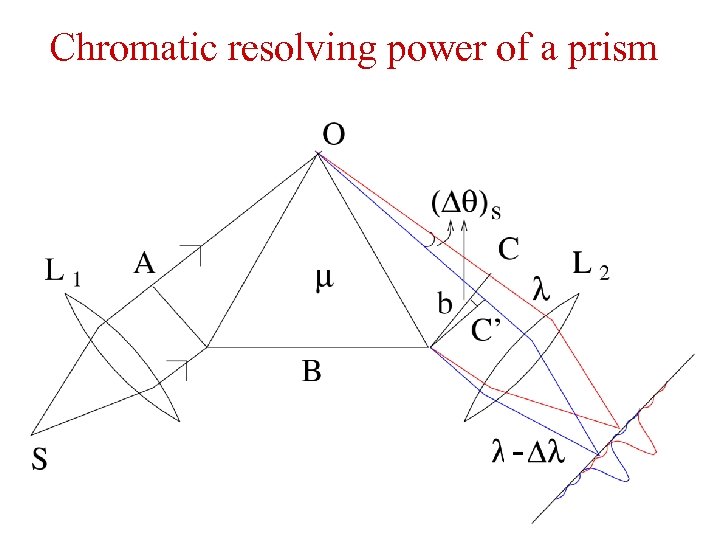 Chromatic resolving power of a prism -
Chromatic resolving power of a prism -
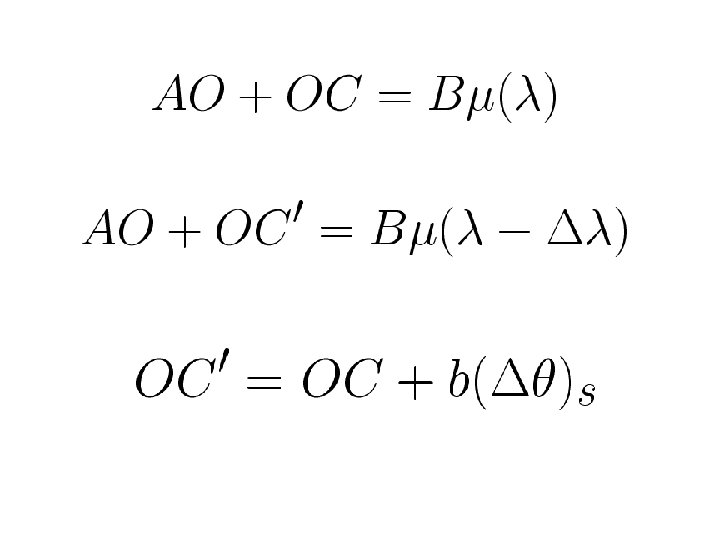
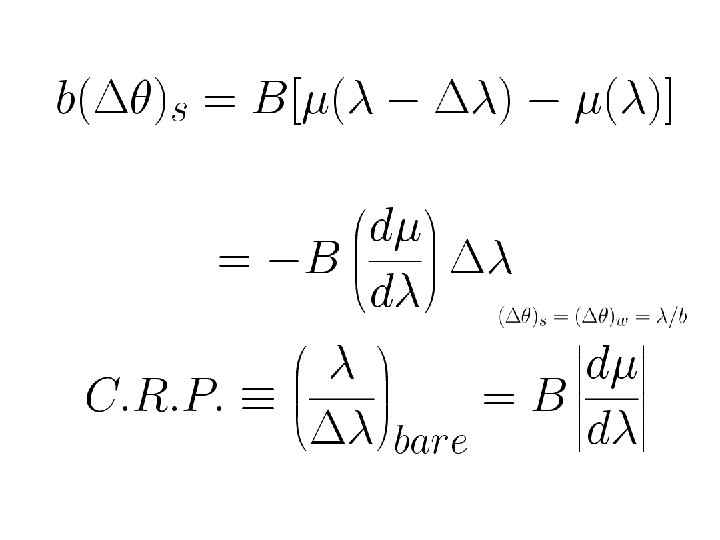
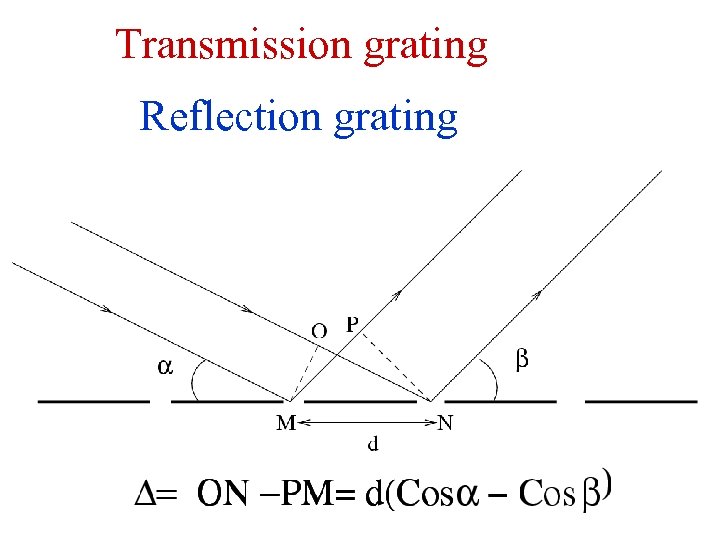 Transmission grating Reflection grating
Transmission grating Reflection grating
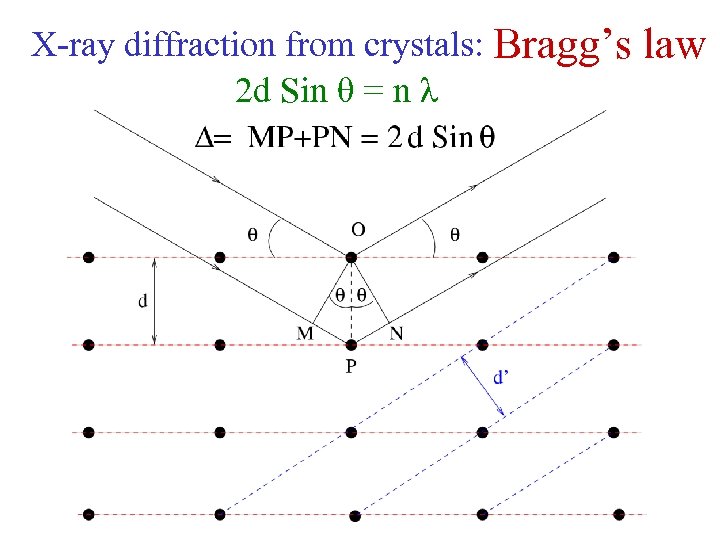 X-ray diffraction from crystals: Bragg’s 2 d Sin θ = n λ law
X-ray diffraction from crystals: Bragg’s 2 d Sin θ = n λ law
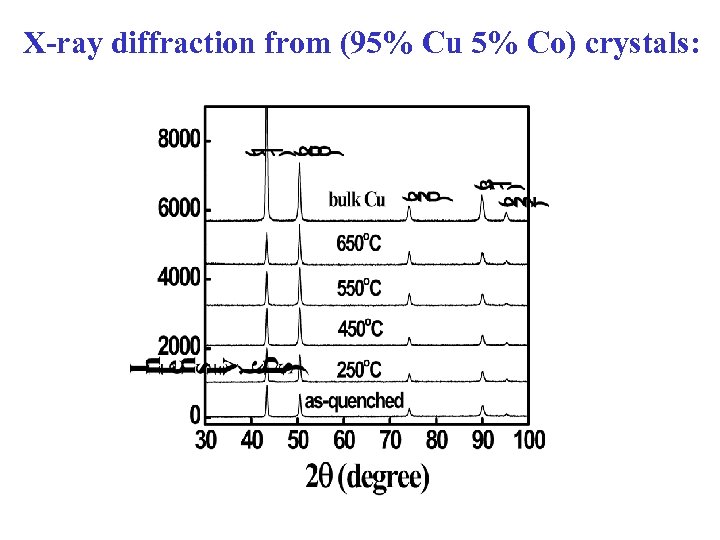 X-ray diffraction from (95% Cu 5% Co) crystals:
X-ray diffraction from (95% Cu 5% Co) crystals:

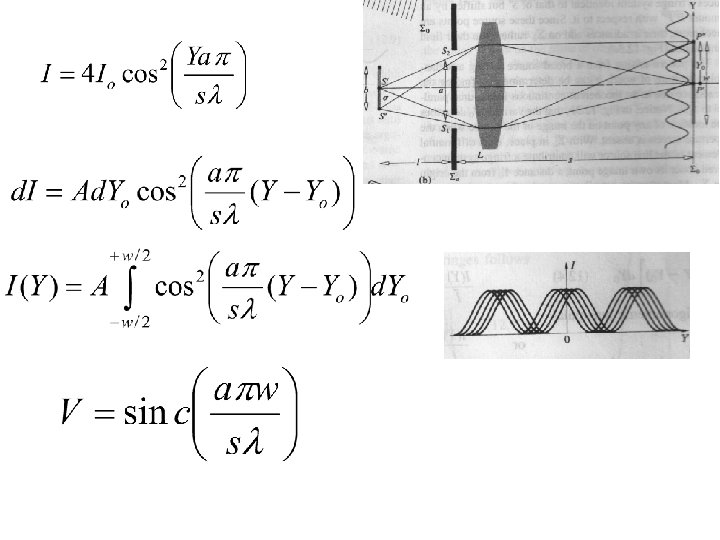
 Visibility of the fringes (V) Maximum and adjacent minimum of the fringe system Reference: Eugene Hecht, Optics, 4 th Ed. Chapter 12 69
Visibility of the fringes (V) Maximum and adjacent minimum of the fringe system Reference: Eugene Hecht, Optics, 4 th Ed. Chapter 12 69