Дифференциальные уравнения Внимание Это сокращенный вариант лекции для

Дифференциальные уравнения Внимание! Это сокращенный вариант лекции для Internet. Лекция 2

План лекции • Понятие дифференциального уравнения первого порядка. • Виды дифференциальных уравнений и способы их решения. • Составление и решение дифференциальных уравнений в задачах физики, химии и биологии.

Дифференциальным уравнением порядка r Называется F[x, y(x), y (x), … y(r)(x)]=0, которое связывает независимое переменное x, искомую функцию y=y(x) и ее производные y (x), … y(r)(x). Порядок r задает наивысший порядок входящих в него производных.

Дифференциальные уравнения Процесс нахождения решения (интегрирование) дифференциального уравнения это поиск функций (решений, интегралов) y=y(x), удовлетворяющих этому уравнению для всех значений x в определенном интервале (a, b). Решения могут быть проверены подстановкой в исходное уравнение.

Дифференциальные уравнения первого порядка 1 тип или y (x)=f(x). Решение: 1 этап разделение переменных, надо добиться того, чтобы переменная x находилась в одной части равенства, а y - в другой. умножая обе части на dx: dy= f(x)dx, 2 этап, интегрируя обе части: y=F(x)+C,

Дифференциальные уравнения первого порядка Решение: разделение переменных, умножая обе части на dx, имеем dy=x 5 dx. затем, интегрируя обе части, получим

Дифференциальные уравнения первого порядка общее решение для Введем начальное условие для y, например, y(0)=88, тогда, получим частное решение вида

Дифференциальные уравнения первого порядка 2 тип где f(y) 0. Решение: 1 этап разделение переменных, умножаем обе части равенства на dx и делим на f(y) 2 этап, интегрируя обе части: F(y)=x+C,

Радиоактивный распад Скорость распада (активность радиоактивного вещества) тем больше, чем больше взято радиоактивного вещества. Если, в каждом грамме радиоактивного вещества за 1 с распадается 0, 001 г, то в двух граммах этого вещества за 1 с распадется 0, 002 г, а в пяти граммах за 1 с - 0, 005 г и т. д. Таким образом, скорость распада прямо пропорциональна массе m имеющегося радиоактивного вещества.

Радиоактивный распад при условии m(0)=m 0. Решение: 1 этап разделение переменных, умножаем обе части равенства на dt и делим на m 2 этап, интегрируя обе части:

Радиоактивный распад 3 этап, преобразования по определению логарифма где C 1= e. C. Если в начальный момент времени t=0 масса равна m 0, то C= m 0, т. е. будем иметь частное решение вида m(t) = m 0 e-kt.

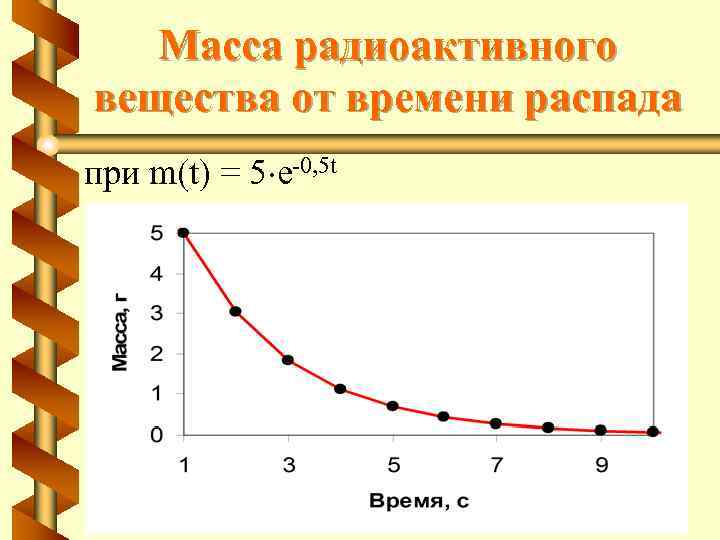Масса радиоактивного вещества от времени распада при m(t) = 5 e-0, 5 t

Дифференциальные уравнения второго порядка Линейное однородное с постоянными коэффициентами a и b: или Составим характеристическое уравнение, используя пробное решение вида: у =Cekx. Причем у =Ckekx и у =Ck 2 ekx.

Дифференциальные уравнения второго порядка Cekx(k 2+a k+b)=0 k 2+a k+b=0 Решаем квадратное характеристическое уравнение, k 2+a k+b=0 1. Корни вещественные и k 1=k 2, тогда у=C 1 ek 1 x+C 2 xek 1 x

Дифференциальные уравнения второго порядка 2. Корни вещественные и k 1 k 2: у=C 1 ek 1 x+C 2 ek 2 x 3. Корни комплексные и k 1= +i , k 2= -i : y=e x(C 1 cos x+C 2 sin x), где

Комплексные числа Например, если k 2 - b= 0, то k 1, 2= Формула Эйлера: eix= cos x + i sin x Поэтому если k 1= +i , то по формуле Эйлера ek 1 x=e x C 0(cos x+i sin x)

Литература 1. Шаповалов К. А. Основы высшей математики. - Красноярск: ООО Печатные технологии , 2004. - С. 47 -61.

Благодарю за внимание!