Дифференциальные уравнения с частными производными 1 2 3

Дифференциальные уравнения с частными производными 1. 2. 3. 4. 5. 6. Основные понятия Понятие разностных схем Разностная схема уравнения теплопроводности Алгоритм решения дифуравнений с частными производными методом сеток Дифуравнение 2 порядка с частными производными Лапласа (эллиптическое) Задача Дирихле

Дифференциальные уравнения с частными производными. Основные понятия • Если искомые функции зависят от нескольких переменных и уравнение содержит производные функции по этим переменным, такие уравнения называются дифференциальными уравнениями с частными производными

Уравнение переноса

КР

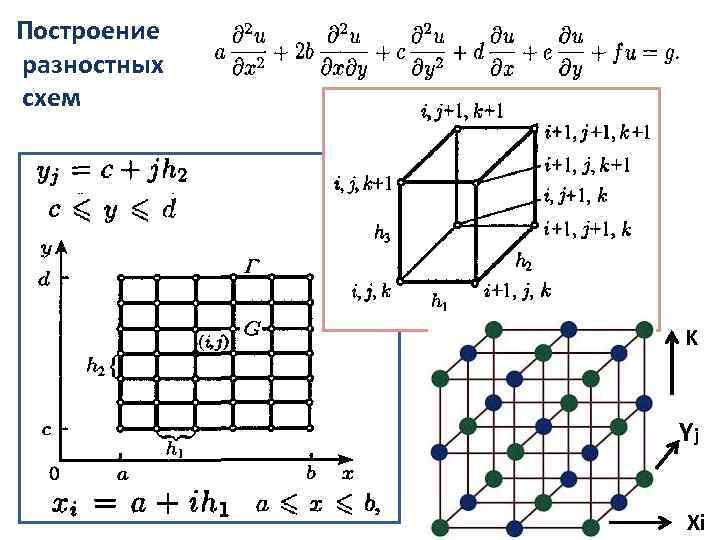Построение разностных схем K Yj Xi

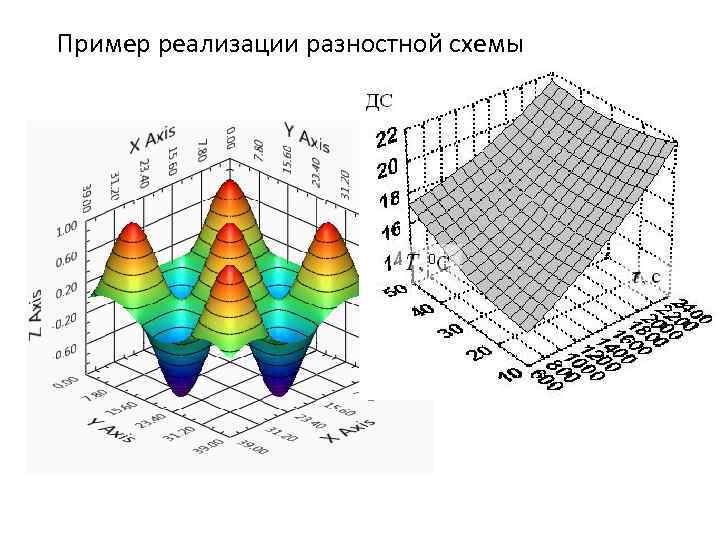Пример реализации разностной схемы

Пример построения разностной схемы уравнения теплопроводности (параболическое)

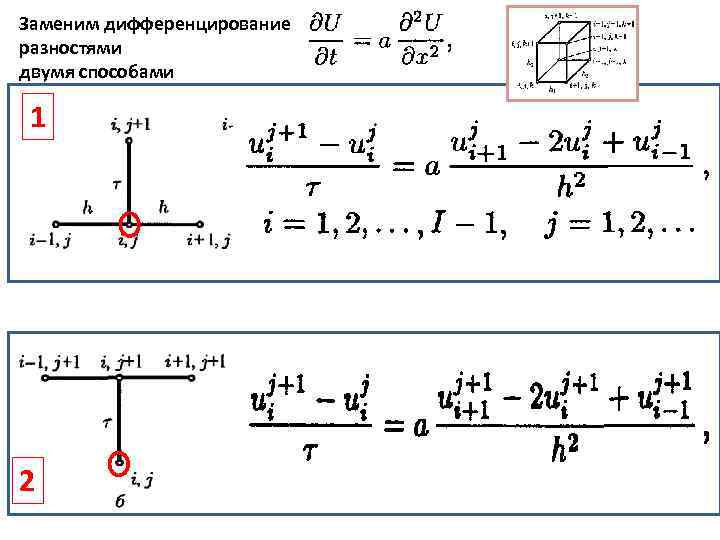Заменим дифференцирование разностями двумя способами 1 2

Далее составим разностные уравнения для всех узлов сетки, частности i=1, J=0 i=2, J=0 Система линейных уравнений относительно неизвестных ……………. . Начальные или краевые условия

Алгоритм решения дифференциальных уравнений с частными производными методом сеток. 1. Область определения функции разбивается сеткой на узлы (граничные и внутренние). 2. Дифференциальное уравнение с частными производными записывается в виде разностной схемы. 3. Для узлов записываются система уравнений с использованием разностных схем. 4. В составленную систему уравнений дописываются уравнения дополнительных условий (начальные или краевые) 5. Полученная система линейных уравнений решается относительно значений функции в узлах. Полученные значения есть решение дифуравнения с частными производными

Дифференциальное уравнение второго порядка с частными производными Лапласа (эллиптическое) КР

В данном случае для построения разностной схемы будет использована следующая разностная схема Алгоритм решения аналогичен предыдущему KP

Задача Дирихле Уравнение Пуассона, при F(x, y, z)=0 – уравнение Лапласа

Итерационный метод решения задачи Дирихле Для каждого центрального узла записывается уравнение, выражающее значение функции в этой точке Значение функции в граничных узлах определяются исходя из начальных условий

Алгоритм решения задачи Дирихле итерационным методом аналогичен методу Гаусса-Зейделля. Задаются некоторые начальные значения , например, равными нулю. Далее находятся первые итерационные значения неизвестных. Полученные значения подставляются в эти же уравнения и находятся вторые итерационные значения. Вычисления продолжаются до тех пор, пока разница между предыдущим и последующим значениями неизвестных для всех неизвестных не станет равна или меньше заданной погрешности. end