Скачать презентацию Дифференциальные уравнения Линейные уравнения с постоянными коэффициентами Скачать презентацию Дифференциальные уравнения Линейные уравнения с постоянными коэффициентами

Lection_18.ppt

  • Количество слайдов: 35

Дифференциальные уравнения Линейные уравнения с постоянными коэффициентами Дифференциальные уравнения Линейные уравнения с постоянными коэффициентами

Линейные уравнения с постоянными коэффициентами n Однородные Д. У. с постоянными коэффициентами. n Рассмотрим Линейные уравнения с постоянными коэффициентами n Однородные Д. У. с постоянными коэффициентами. n Рассмотрим уравнение n n где - постоянные действительные числа Пусть функция - решение Д. У. - корень алгебраического уравнения

Линейные уравнения с постоянными коэффициентами n Определение. n Алгебраическое уравнение соответствующее данному ЛОДУ, n Линейные уравнения с постоянными коэффициентами n Определение. n Алгебраическое уравнение соответствующее данному ЛОДУ, n называется характеристическим уравнением. n Обратное утверждение: n Пусть - корень характеристического уравнения. n Тогда функция -частное решение ЛОДУ. n n Замечание. Алгебраическое уравнение степени n с действительными коэффициентами имеет n решений.

Линейные уравнения с постоянными коэффициентами n Примеры. n 1. n Замена: n Характеристическое уравнение: Линейные уравнения с постоянными коэффициентами n Примеры. n 1. n Замена: n Характеристическое уравнение: n n - частные решения ЛОДУ.

Линейные уравнения с постоянными коэффициентами n Примеры. n 2. n Замена: n Характеристическое уравнение: Линейные уравнения с постоянными коэффициентами n Примеры. n 2. n Замена: n Характеристическое уравнение: n n - частные решения ЛОДУ.

Линейные уравнения с постоянными коэффициентами n Свойства решений ЛОДУ. n 1. Линейность. - решения Линейные уравнения с постоянными коэффициентами n Свойства решений ЛОДУ. n 1. Линейность. - решения ЛОДУ n - решение ЛОДУ. n n Доказать самостоятельно.

Линейные уравнения с постоянными коэффициентами n Свойства решений ЛОДУ. n 1. Линейность. - решения Линейные уравнения с постоянными коэффициентами n Свойства решений ЛОДУ. n 1. Линейность. - решения ЛОДУ n - решение ЛОДУ. n n Доказать самостоятельно. n Примеры. n 1. - решение ЛОДУ n при любых постоянных С 1 и С 2. n 2. - решение ЛОДУ n при любых постоянных С 1 и С 2.

Линейные уравнения с постоянными коэффициентами n 2. Критерий линейной независимости системы решений ЛОДУ. Пусть Линейные уравнения с постоянными коэффициентами n 2. Критерий линейной независимости системы решений ЛОДУ. Пусть n - частные решения ЛОДУ порядка n в n n Теорема. Система функций n линейно независимая в n .

Линейные уравнения с постоянными коэффициентами n Определение ФСР. n Фундаментальной системой решений (ФСР) n Линейные уравнения с постоянными коэффициентами n Определение ФСР. n Фундаментальной системой решений (ФСР) n ЛОДУ - порядка n n называется система n n линейно независимых решений ЛОДУ.

Линейные уравнения с постоянными коэффициентами n Определение ФСР. n Фундаментальной системой решений (ФСР) n Линейные уравнения с постоянными коэффициентами n Определение ФСР. n Фундаментальной системой решений (ФСР) n ЛОДУ - порядка n n называется система n n линейно независимых решений ЛОДУ. n Примеры. n 1. n 2. - ФСР ЛОДУ

Линейные уравнения с постоянными коэффициентами n Теорема о структуре общего решения ЛОДУ. n Пусть Линейные уравнения с постоянными коэффициентами n Теорема о структуре общего решения ЛОДУ. n Пусть при система n образует ФСР ЛОДУ порядка n. n Тогда общее решение ЛОДУ порядка n n имеет вид n с произвольными постоянными n Примеры. n 1. , - общее решение ЛОДУ n 2. , - общее решение ЛОДУ

Линейные уравнения с постоянными коэффициентами n ФСР в случае различных действительных корней. Доказательство (при Линейные уравнения с постоянными коэффициентами n ФСР в случае различных действительных корней. Доказательство (при n=2). 1. 2. образуют ФСР

Линейные уравнения с постоянными коэффициентами n n Случай кратных действительных корней. Пусть действительное число Линейные уравнения с постоянными коэффициентами n n Случай кратных действительных корней. Пусть действительное число - корень уравнения кратности В ФСР ЛОДУ ему соответствуют решений вида

Линейные уравнения с постоянными коэффициентами n Случай кратных действительных корней. n Пусть действительное число Линейные уравнения с постоянными коэффициентами n Случай кратных действительных корней. n Пусть действительное число - корень уравнения кратности В ФСР ЛОДУ ему соответствуют решений вида n n n Пример. 1. 2. Замена: 3. Характеристическое уравнение: (кратность 2) n n 4. ФСР:

Линейные уравнения с постоянными коэффициентами n ФСР в случае, когда некоторые корни комплексные. n Линейные уравнения с постоянными коэффициентами n ФСР в случае, когда некоторые корни комплексные. n n n 1. Случай простого комплексного корня. Пусть - комплексный корень характеристического уравнения тогда - также корень этого уравнения. n n n Функции - решения ЛОДУ. Функции линейно независимые, так как § Функции вместе с другими (n-2) линейно независимыми решениями ЛОДУ образуют ФСР.

Линейные уравнения с постоянными коэффициентами n Преобразуем функции с помощью формулы Эйлера: n Функции Линейные уравнения с постоянными коэффициентами n Преобразуем функции с помощью формулы Эйлера: n Функции n § являются действительными функциями переменной х; § являются решениями ЛОДУ; § являются линейно независимыми Образуют (вместе с другими) ФСР

Линейные уравнения с постоянными коэффициентами Примеры. n 1. Найти ФСР уравнения n Шаг 1. Линейные уравнения с постоянными коэффициентами Примеры. n 1. Найти ФСР уравнения n Шаг 1. Запишем характеристическое уравнение и решим его: n n Шаг 2. Запишем ФСР ЛОДУ:

Линейные уравнения с постоянными коэффициентами Примеры. n 2. Найти ФСР уравнения n Шаг 1. Линейные уравнения с постоянными коэффициентами Примеры. n 2. Найти ФСР уравнения n Шаг 1. Запишем характеристическое уравнение и решим его: n n Шаг 2. Запишем ФСР ЛОДУ:

Линейные уравнения с постоянными коэффициентами n n n 2. Случай кратных комплексных корней. Пусть Линейные уравнения с постоянными коэффициентами n n n 2. Случай кратных комплексных корней. Пусть комплексное число корень кратности число - тоже корень кратности В ФСР ЛОДУ им соответствуют решений вида

Линейные уравнения с постоянными коэффициентами n Неоднородные уравнения с постоянными коэффициентами. n Свойства решений Линейные уравнения с постоянными коэффициентами n Неоднородные уравнения с постоянными коэффициентами. n Свойства решений ЛНДУ. . n 1. - частные решения ЛНДУ n n - решение ЛОДУ , соответствующего данному ЛНДУ.

Линейные уравнения с постоянными коэффициентами n Неоднородные уравнения с постоянными коэффициентами. n Свойства решений Линейные уравнения с постоянными коэффициентами n Неоднородные уравнения с постоянными коэффициентами. n Свойства решений ЛНДУ. . n 1. - частные решения ЛНДУ - решение ЛОДУ , соответствующего данному ЛНДУ. n n n Доказательство.

Линейные уравнения с постоянными коэффициентами n 2. Принцип суперпозиции. Линейные уравнения с постоянными коэффициентами n 2. Принцип суперпозиции.

Линейные уравнения с постоянными коэффициентами n 2. Принцип суперпозиции. Доказательство. Линейные уравнения с постоянными коэффициентами n 2. Принцип суперпозиции. Доказательство.

Линейные уравнения с постоянными коэффициентами n Теорема о структуре общего решения ЛНДУ. n 1. Линейные уравнения с постоянными коэффициентами n Теорема о структуре общего решения ЛНДУ. n 1. n 2. n - частное решение ЛНДУ - ФСР ЛОДУ соответствующего данному ЛНДУ. Общее решение ЛНДУ имеет вид - произвольные постоянные порядка n. ,

Линейные уравнения с постоянными коэффициентами n Неоднородные уравнения с постоянными коэффициентами. n Метод неопределенных Линейные уравнения с постоянными коэффициентами n Неоднородные уравнения с постоянными коэффициентами. n Метод неопределенных коэффициентов. n Рассмотрим уравнение n где - постоянные коэффициенты и имеет специальный вид. Правило.

Линейные уравнения с постоянными коэффициентами Примеры. n 1. Найти общее решение уравнения n Шаг Линейные уравнения с постоянными коэффициентами Примеры. n 1. Найти общее решение уравнения n Шаг 1. Решим ЛОДУ, соответствующее данному ЛНДУ: n n Шаг 2. Найдем частное решение ЛНДУ: n Шаг 3. Запишем общее решение ЛНДУ:

Линейные уравнения с постоянными коэффициентами 2. Найти общее решение ЛНДУ n Шаг 1. Решим Линейные уравнения с постоянными коэффициентами 2. Найти общее решение ЛНДУ n Шаг 1. Решим ЛОДУ, соответствующее данному ЛНДУ: n n Шаг 2. Найдем частное решение ЛНДУ: n Шаг 3. Запишем общее решение ЛНДУ:

Линейные уравнения с постоянными коэффициентами Пример 3. Найти общее решение ЛНДУ n Шаг 1. Линейные уравнения с постоянными коэффициентами Пример 3. Найти общее решение ЛНДУ n Шаг 1. Решим ЛОДУ, соответствующее данному ЛНДУ: n n Шаг 2. Найдем частное решение ЛНДУ: n Шаг 3. Запишем общее решение ЛНДУ:

Линейные уравнения с постоянными коэффициентами n n Пример 4. Найти общее решение ЛНДУ Шаг Линейные уравнения с постоянными коэффициентами n n Пример 4. Найти общее решение ЛНДУ Шаг 1. Решим ЛОДУ, соответствующее данному ЛНДУ: n Шаг 2. Найдем частное решение ЛНДУ: n Шаг 3. Запишем общее решение: : резонанс

Линейные уравнения с постоянными коэффициентами Линейные неоднородные Д. У. n Метод вариации произвольных постоянных Линейные уравнения с постоянными коэффициентами Линейные неоднородные Д. У. n Метод вариации произвольных постоянных (метод Лагранжа). n Теорема. n - ЛНДУ порядка n с непрерывными коэффициентами. - ФСР ЛОДУ, соответствующего данному ЛНДУ n

Линейные уравнения с постоянными коэффициентами Частный случай. n Рассмотрим ЛНДУ второго порядка n Пусть Линейные уравнения с постоянными коэффициентами Частный случай. n Рассмотрим ЛНДУ второго порядка n Пусть n Тогда n - ФСР соответствующего ЛОДУ.

Линейные уравнения с постоянными коэффициентами n Пример. Решение. n 1. ЛОДУ n 2. Общее Линейные уравнения с постоянными коэффициентами n Пример. Решение. n 1. ЛОДУ n 2. Общее решение ЛОДУ n 3. Частное решение ЛНДУ n 4. Найдем n n 5. Общее решение ЛНДУ ФСР

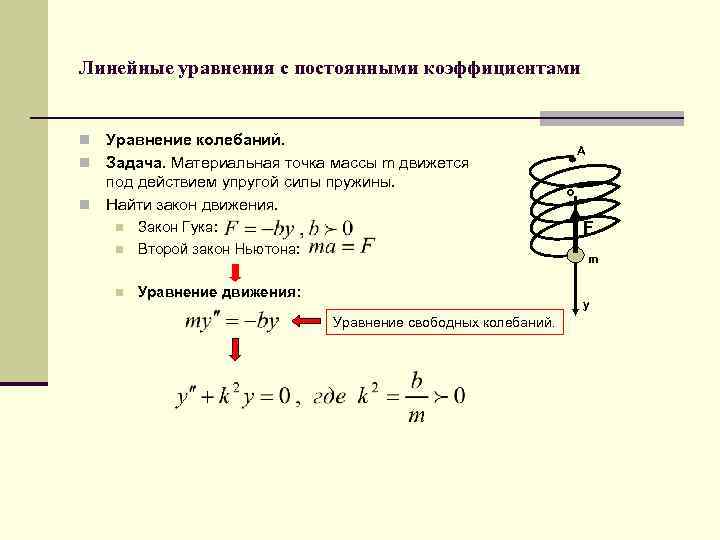Линейные уравнения с постоянными коэффициентами Уравнение колебаний. n Задача. Материальная точка массы m движется Линейные уравнения с постоянными коэффициентами Уравнение колебаний. n Задача. Материальная точка массы m движется под действием упругой силы пружины. n Найти закон движения. n n n o F Закон Гука: Второй закон Ньютона: Уравнение движения: n A m y Уравнение свободных колебаний.

Линейные уравнения с постоянными коэффициентами n Характеристическое уравнение: n n ФСР: Общее решение: n Линейные уравнения с постоянными коэффициентами n Характеристическое уравнение: n n ФСР: Общее решение: n Задача Коши. Свободные колебания с амплитудой и начальной фазой - частота собственных колебаний

Линейные уравнения с постоянными коэффициентами n n Вынужденные колебания. Резонанс. - внешняя сила n Линейные уравнения с постоянными коэффициентами n n Вынужденные колебания. Резонанс. - внешняя сила n n - амплитуда, - частота внешней силы. Уравнение вынужденных колебаний. - отсутствие резонанса - резонанс