 Дифференциальные уравнения 1
Дифференциальные уравнения 1
 Общие понятия 2
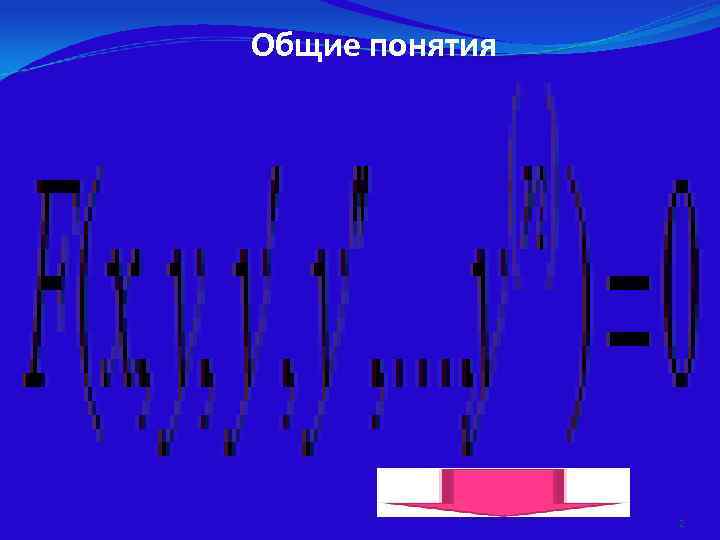
Общие понятия 2
 Дифференциальные уравнения разделяются на две группы: обыкновенные и в частных производных. Уравнения, содержащие производные от частные производные неизвестной функции от неизвестной функции лишь одной независимой по нескольким переменной, называются обыкновенными независимым дифференциальными переменным, уравнениями. называются дифференциальными уравнениями в частных производных. 3
Дифференциальные уравнения разделяются на две группы: обыкновенные и в частных производных. Уравнения, содержащие производные от частные производные неизвестной функции от неизвестной функции лишь одной независимой по нескольким переменной, называются обыкновенными независимым дифференциальными переменным, уравнениями. называются дифференциальными уравнениями в частных производных. 3
 4
4
 Примеры ДУ различных порядков 5
Примеры ДУ различных порядков 5
 6
6
 7
7
 Задача Коши для дифференциальных уравнений 8
Задача Коши для дифференциальных уравнений 8
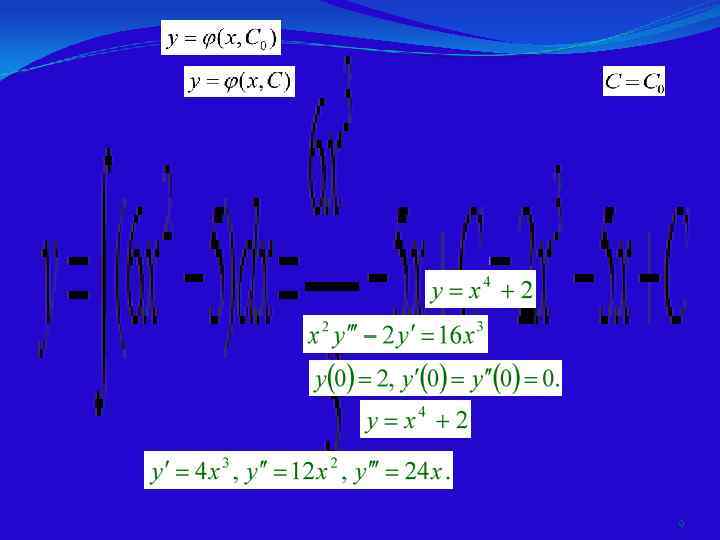 9
9
 10
10
 Геометрическая интерпретация задачи Коши 11
Геометрическая интерпретация задачи Коши 11
 Геометрическая интерпретация задачи Коши 12
Геометрическая интерпретация задачи Коши 12
 13
13
 Основные типы интегрируемых дифференциальных уравнений первого порядка 1. Простейшие дифференциальные уравнения Дифференциальные уравнения этого типа имеет вид: (1) или Способ решения ДУ этого типа состоит в интегрировании обеих частей уравнения. Пример. Решить ДУ . . Решение. Представим данное уравнение в следующем виде 14
Основные типы интегрируемых дифференциальных уравнений первого порядка 1. Простейшие дифференциальные уравнения Дифференциальные уравнения этого типа имеет вид: (1) или Способ решения ДУ этого типа состоит в интегрировании обеих частей уравнения. Пример. Решить ДУ . . Решение. Представим данное уравнение в следующем виде 14
 Интегрируя обе части, получим Пример. Найти частное решение дифференциального уравнения При начальном условии Решение. . Интегрируя обе части ДУ по частям, получим 15
Интегрируя обе части, получим Пример. Найти частное решение дифференциального уравнения При начальном условии Решение. . Интегрируя обе части ДУ по частям, получим 15
 Найдем частное решение, соответствующее начальному условию: Подставим в начальное условие 16
Найдем частное решение, соответствующее начальному условию: Подставим в начальное условие 16
 Линейные дифференциальные уравнения первого порядка Определение. Линейными дифференциальными уравнениями первого порядка называются уравнения следующего вида где и - данные непрерывные на функции. Если для всех , то уравнение называется линейным однородным ДУ. Рассмотрим оба случая линейных (ДУ) 1 -го порядка: однородные и неоднородные. 17
Линейные дифференциальные уравнения первого порядка Определение. Линейными дифференциальными уравнениями первого порядка называются уравнения следующего вида где и - данные непрерывные на функции. Если для всех , то уравнение называется линейным однородным ДУ. Рассмотрим оба случая линейных (ДУ) 1 -го порядка: однородные и неоднородные. 17
 Cл. 1. Однородные линейные ДУ первого порядка некоторые непрерывные функции на . Если для всех значений уравнение называется однородным . Данное уравнение является ДУ с разделяющимися переменными, поэтому его решение состоит из двух этапов • разделения переменных: • интегрирования обеих частей: 18
Cл. 1. Однородные линейные ДУ первого порядка некоторые непрерывные функции на . Если для всех значений уравнение называется однородным . Данное уравнение является ДУ с разделяющимися переменными, поэтому его решение состоит из двух этапов • разделения переменных: • интегрирования обеих частей: 18
 Окончательно - общее решение однородного линейного ДУ. Проверка показывает, что удовлетворяет уравнению, поэтому также является решением данного ДУ. Ответ: , 19
Окончательно - общее решение однородного линейного ДУ. Проверка показывает, что удовлетворяет уравнению, поэтому также является решением данного ДУ. Ответ: , 19
 Если однородное дифференциальное уравнение удовлетворяет некоторому начальному условию то легко показать, что частное решение ДУ примет вид: 20
Если однородное дифференциальное уравнение удовлетворяет некоторому начальному условию то легко показать, что частное решение ДУ примет вид: 20
 Линейные неоднородные уравнения 21
Линейные неоднородные уравнения 21
 Общее решение Произвольная постоянная С заменяется на неизвестную функцию . Далее ищется общее решение ДУ в виде , где - неизвестная функция. Для нахождения этой функции общее решение уравнения подставляем в исходное дифференциальное уравнение получим следующее 22
Общее решение Произвольная постоянная С заменяется на неизвестную функцию . Далее ищется общее решение ДУ в виде , где - неизвестная функция. Для нахождения этой функции общее решение уравнения подставляем в исходное дифференциальное уравнение получим следующее 22
 23
23
 Пример 1. Найти общее решение ДУ 24
Пример 1. Найти общее решение ДУ 24
 Дифференцируя обе части , получим Где - произвольная постоянная. Подставляя полученные результаты в общий вид решения, получим Ответ: 25
Дифференцируя обе части , получим Где - произвольная постоянная. Подставляя полученные результаты в общий вид решения, получим Ответ: 25
