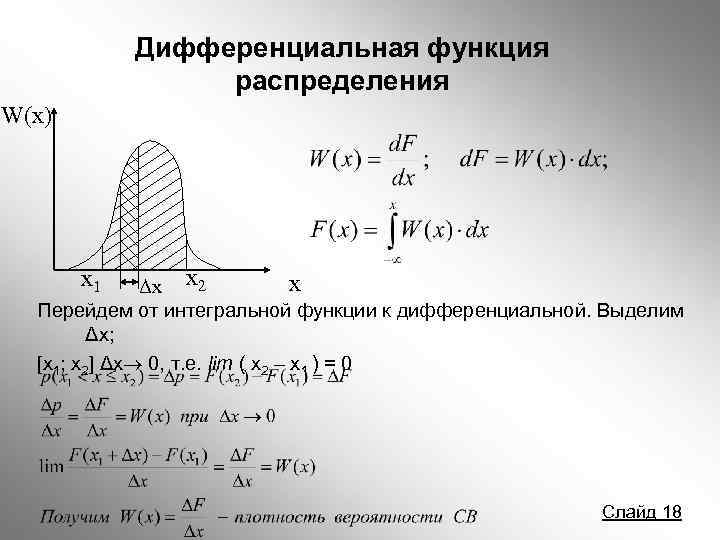
Дифференциальная функция распределения W(x) x Δx x 2 Перейдем от интегральной функции к дифференциальной. Выделим Δx; [x 1; x 2] Δx 0, т. е. lim ( x 2 – x 1 ) = 0 x 1 Слайд 18
Дифференциальная функция распределения Свойства дифференциальной функции распределения: 1. W(x) 0 W(x) = max – наиболее вероятное значение 2. - условие нормировки 3. Вероятность “p” попадания СВ с [a; b] Слайд 19
Моменты (параметры) распределения СВ Числовые характеристики СВ СВ k = 1, 2, 3… - порядок момента Начальные моменты k=1 k 2 = 2 Слайд 20
Моменты (параметры) распределения СВ Центральные моменты Дисперсия СВ Слайд 21
Моменты (параметры) распределения СВ Свойства мат. ожидания и дисперсии Слайд 22
Виды функций распределения СВ. Нормальный закон x 1 ОИ xд СИ x 2 … xn Слайд 23
Виды функций распределения СВ. Равномерный закон распределения Дифференциальный 1 b-a S=1 a m 1 b Слайд 24
Скачать презентацию Дифференциальная функция распределения W x x Δx x 2
Лекции МСС версия 180313.ppt