DIDÁCTICA DE LAS MATEMÁTICAS EN MATEMÁTICAS PARA TODOS

DIDÁCTICA DE LAS MATEMÁTICAS EN MATEMÁTICAS PARA TODOS Instituto APOYO Mercedes G. de Valenzuela cvalenzuela@trener. edu. pe Jorge Ferradas jferrada@trener. edu. pe

Cuatro preocupaciones centrales Las características de la etapa del desarrollo humano en que se encuentra el estudiante. Los contenidos y las competencias del área a enseñar. “Cómo” se enseña -es decir el manejo adecuado de las estrategias didácticas generales y propias del área. Bolívar (2005), “el modo cómo los alumnos comprenden un tópico disciplinar, sus posibles malentendidos y grado de dificultad”.

¿Qué es el aprendizaje de las matemáticas? María Antonia Canals Tolosa en una de las conferencias plenarias del 10º “Congreso castellano y leonés de educación matemática” dice, citando a alguien, que: “Aprender es construir un significado personal de un contenido científico o cultural ya existente”

En un polo el contenido ya existente, y en el otro: “… este camino no se forma como una serie lineal de puntos, sino más bien como un tejido en forma de red, con unos nudos que se van creando y entrelazando de distinto modo para cada persona, y del cual, como de tantas cosas en las que interviene nuestro cerebro, todavía nos falta mucho por conocer. ” María Antonia Canals Tolosa

Otra manera de decirlo … “Aprendizaje significativo es el proceso que se genera en la mente humana cuando subsume nuevas informaciones de manera no arbitraria y sustantiva y que requiere como condiciones: predisposición para aprender y material potencialmente significativo que, a su vez, implica significatividad lógica de dicho material y la presencia de ideas de anclaje en la estructura cognitiva del que aprende. ” La teoría del aprendizaje significativo Mª Luz Rodríguez Palmero

Competencias matemáticas 1. Desarrolla estrategias matemáticas para resolver problemas. 2. Comprende, relaciona, interpreta y aplica conceptos matemáticos. 3. Interpreta y utiliza el lenguaje matemático para registrar y comunicar. 4. Utiliza efectivamente procedimientos matemáticos. 5. Explora y sustenta enunciados matemáticos.

Además … Manual de docentes MPT Un buen aprendizaje de las matemáticas inculca hábitos, actitudes y valores, como: • La toma de decisiones acertadas • La capacidad de entender y formular con precisión problemas • El hábito de trabajar con datos y cifras al analizar alternativas • La prolijidad, laboriosidad y atención a los detalles • El amor a la verdad y la confianza en el trabajo De esta manera contribuye a formar el pensamiento lógico matemático, imprescindible para entender la realidad y participar en una sociedad democrática.

El enfoque didáctico

I Sentido de las matemáticas Partir de casos concretos y de la vida cotidiana Recuperar los saberes previos Integración de diversas áreas intra y extra matemáticas

II Construcción del aprendizaje Acción concreta para descubrir Interacción para acomodar los nuevos saberes Verbalización y representación para hacer visible el aprendizaje

III Consolidación del aprendizaje Avance en espiral Ejercitación no mecánica / juego Uso del error y de la diversidad de soluciones Autocorrección y autoevaluación Retroalimentación y aprendizaje diferenciado

Las fases del aprendizaje Para concretar el enfoque didáctico

1. Inicio Motivación, recuperación de saberes previos y conflicto cognitivo. Actividades que realizaremos para encausar y dar claridad a los alumnos del tema que se revisará (preparan y alertan al estudiante en relación a qué y cómo va a aprender)

Mimate 1 Pg. 33

MPT 1 (Pág. 62)

MPT 2 (Pág. 114)

2. Elaboración o desarrollo Procesar la información, aplicar lo aprendido, transferir a situaciones nuevas, reflexionar sobre lo aprendido y aprender de errores típicos Aquí es donde aplican estrategias que apoyen la construcción de significados de parte del estudiante.

Procesamiento de la información Es el momento para, a partir de las situaciones iniciales discutidas, concluir y formalizar: Se aclara Se generaliza Se formaliza Aplicación de lo aprendido Se resuelven casos básicos Transferencia a situaciones nuevas Se resuelven casos más complejos Reflexión sobre lo aprendido y prevención de errores típicos A lo largo de todo el proceso anterior

Mimate 2 Pg. 25 Uso del cuerpo para medir ¿y si no es exacto? Uso del metro o de la regla ¿y si no es exacto?

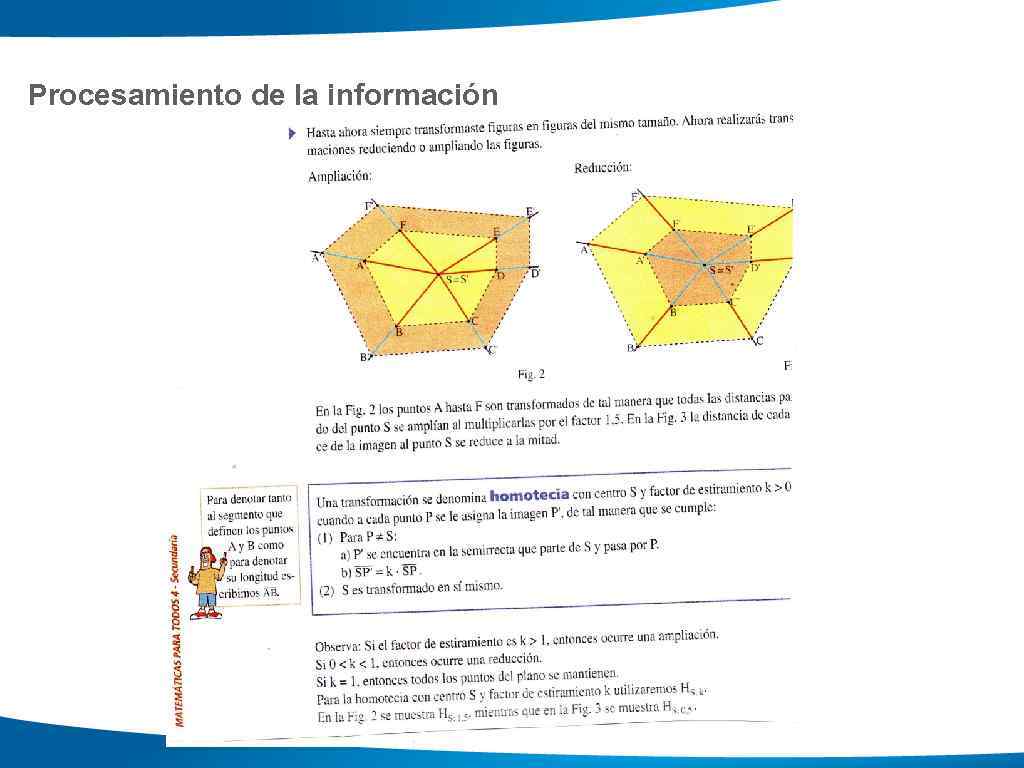Procesamiento de la información

Aplicación de lo aprendido

Transferencia a situaciones nuevas

Reflexión sobre lo aprendido y prevención de errores típicos Observar que el factor de estiramiento multiplica la longitud de SP y el resultado es la longitud SP’. Ambas longitudes se miden desde S. En toda homotecia los puntos S, P y P’ son colineales. Si S y P son coincidentes P’ también lo es, independientemente del valor de k.

3. Cierre Se presenta después del contenido que se ha de aprender y apoya al alumno a formar una visión sintética, integradora. Promueve la sistematización, el resumen y la metacognición, la autoevaluación. Permite la retroalimentación.

Estrategias didácticas

Recuperar Saberes previos a partir de un caso-preguntas-título. Conocimientos matemáticos que son prerrequisitos. (normalmente en la fase de inicio)

Hacerlos protagonistas para construir nociones Lluvia de ideas, o similares, para construcción de conceptos o propiedades a partir de una construcción individual. Promover la discusión en parejas o grupos. Darles oportunidades para que ellos expliquen y para que pregunten. Darles pautas para autocorregir.

Usar lo concreto Material concreto diverso y manipularlo Simulación y juego Movimiento Preguntas. . . y repreguntas

Usar el cuerpo Recortar curvas o armar modelos para entender características de curvas y sólidos. Plantear el movimiento del propio cuerpo como una alternativa para entender algunos conceptos como: Las trayectorias de las curvas (como la circunferencia) Las transformaciones geométricas (traslación, rotación y reflexión) Móviles

El cuerpo como manipulable Problemas de móviles que se alcanzan y se encuentran Cuando se alcanzan, ¿cuál es la idea clave? Cuando se encuentran, ¿cuál es la idea clave? Dos alumnos o alumnas que se alcanzan o que se encuentran van a permitir llegar a esas conclusiones.

Verbalizar Nosotros y ellos en la clase. . . y en las evaluaciones Parafrasear Aclaraciones de vocabulario Uso de analogías Exigir una explicación en la forma de “paso por paso” Escribir comentarios al corregir

Representar Sistematizar con esquemas (de preferencia ir haciéndolos con la clase) Simbolizar Graficar Construir tablas Usar ilustraciones con colores Usar diagramas para procedimientos

El aprendizaje en espiral Mismo tema. . . otra perspectiva Las microsecuencias en espiral abordan un mismo tema desde perspectivas cada vez más complejas. Captan conjuntos complejos en sus rasgos generales y luego se van viendo los matices, los aspectos más específicos. (http: //www. geocities. com/aulauy/secuenciasdeaprendizaje. htm)

Resignificación En este tipo de secuencia se destaca el carácter de bucle recursivo con que cada nuevo enfoque permite resignificar los conocimientos anteriores a la luz de los nuevos saberes adquiridos. Este elemento es lo que diferencia una secuencia en espiral de un procedimiento "paso a paso" en el que solamente se acumulan nuevas destrezas, sin facilitar ese "salto atrás" que permite volver a mirar con ojos nuevos lo ya conocido.

Los manipulables

Ejemplos de manipulables físicos en la fase de inicio: Manipular, recuperar saberes, descubrir, interactuar, comprender y construir el conocimiento.

El caso 1 de la Pág. 88 del libro de MPT 2 plantea: Ejemplo: La desigualdad triangular

La desigualdad triangular … Es una buena práctica plantear el Caso 1 con el libro cerrado y entonces podemos plantear esta pregunta a la clase: ¿Tres segmentos de cualquier longitud pueden ser los lados de un solo triángulo?

La desigualdad triangular … Tenemos dos alternativas: (I) Dejarlos especular simplemente dibujando, lo más probable es que los alumnos y las alumnas no partan de diferentes medidas sino que dibujen muchos triángulos y arriben a una conclusión equivocada: sí se puede. (II) Darles un manipulable sencillo, que es lo que ustedes tienen, palitos de diversas longitudes y, entonces, ellos partirán desde donde esperamos: de “segmentos” de longitudes variables. La conclusión deviene en evidente: no se puede.

La desigualdad triangular … Las siguientes preguntas son: ¿por qué no se puede? ¿qué requisitos o condiciones deben cumplir las longitudes de los segmentos para poder ser lados de un triángulo? La explicación está en el libro: Pero seguirla solo mirando el libro, o la pizarra, es muy diferente a poder comprobar cada situación “en físico”.

La desigualdad triangular … La formalización de la desigualdad triangular es muy importante pero hacerla con un mecanismo físico de comprobación facilita su comprensión y su acomodación al … permitir construir un significado personal. Además fomenta el intercambio de ideas entre pares y con el profesor Se puede aprovechar para insistir en que el contraejemplo basta.

Ejemplo de manipulables para sistematizar: Elementos de sólidos geométricos Algunos elementos no se pueden observar en los desarrollos, por ejemplo la altura de una pirámide o un cono o la diagonal de un paralelepípedo. Los modelos sobre todo los transparentes permiten ver estos elementos. Los modelos, aunque no sean transparentes, permiten observar las tres dimensiones en magnitudes reales cosa que la pizarra no permite

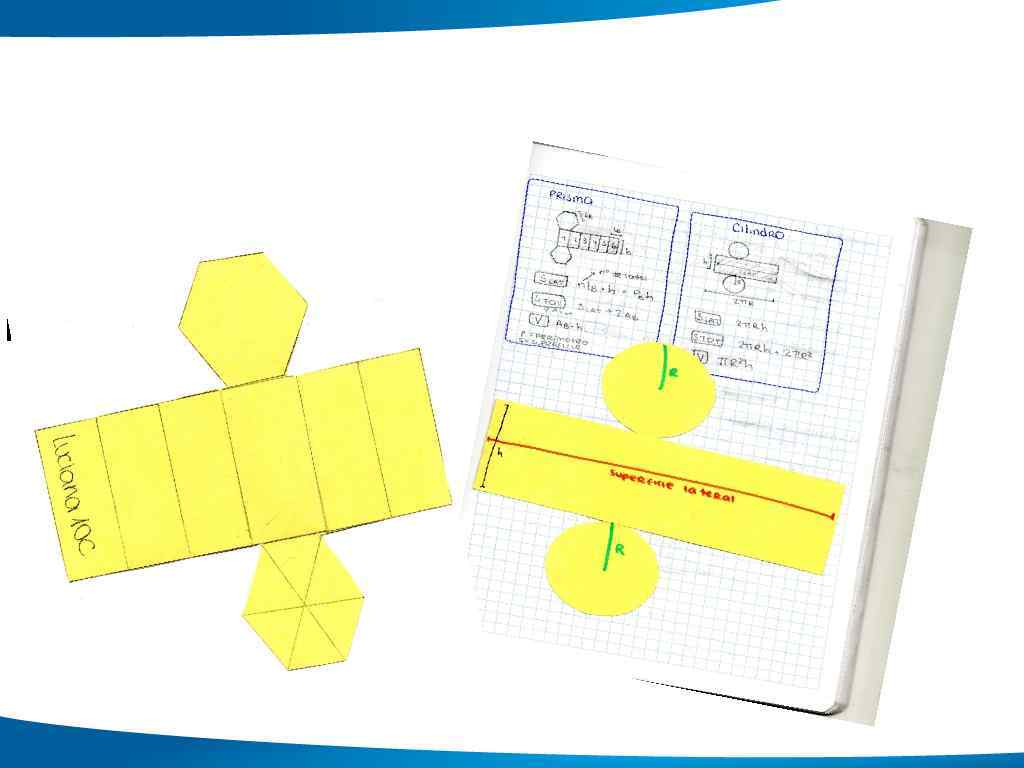Prismas y cilindros

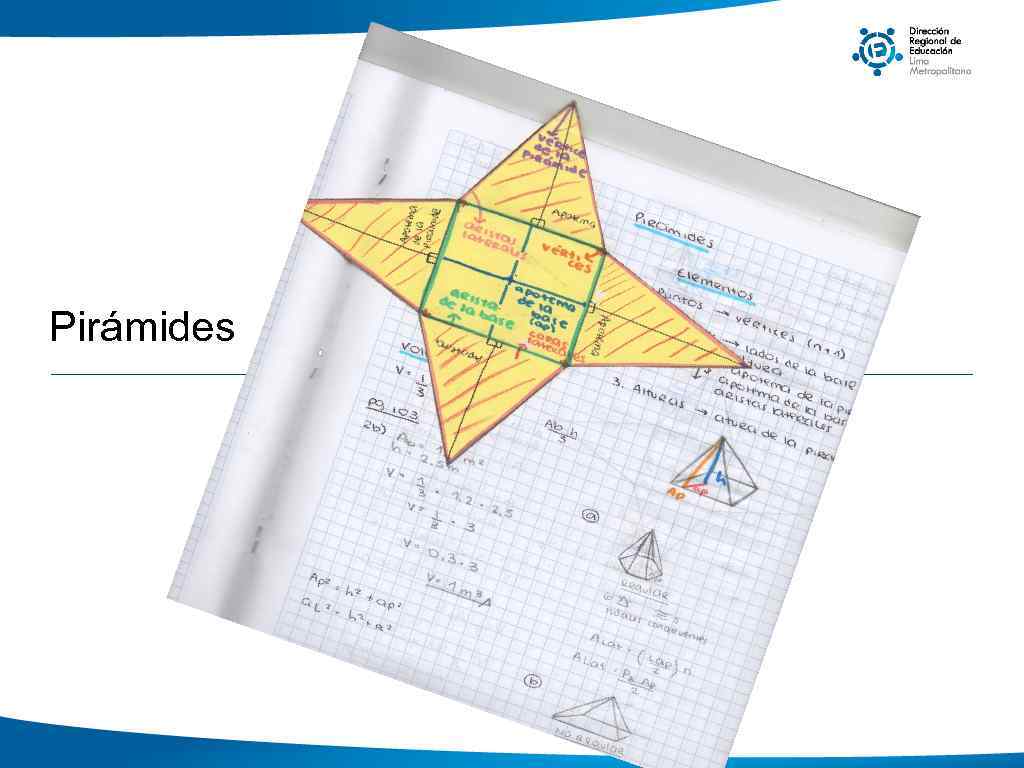Pirámides

Manipulables virtuales: algunas aplicaciones concretas

Manipulables virtuales para geometría Permiten trabajar la geometría de un modo experimental, su característica más importante y su aportación más novedosa es que nos permiten modificar la construcción inicial, manteniendo las propiedades o relaciones que hayamos definido. Permiten la experimentación con el problema, el análisis de casos particulares y de casos extremos, la búsqueda de pautas o relaciones, la elaboración de conjeturas, . . . son procesos, partes todos ellos del razonamiento inductivo, que se abordarán de una forma natural en las actividades desarrolladas con él. Bagazgoitia, Alberto. http: //dialnet. unirioja. es/servlet/oaiart? codigo=803919(Revista) ISSN 1131 -7787

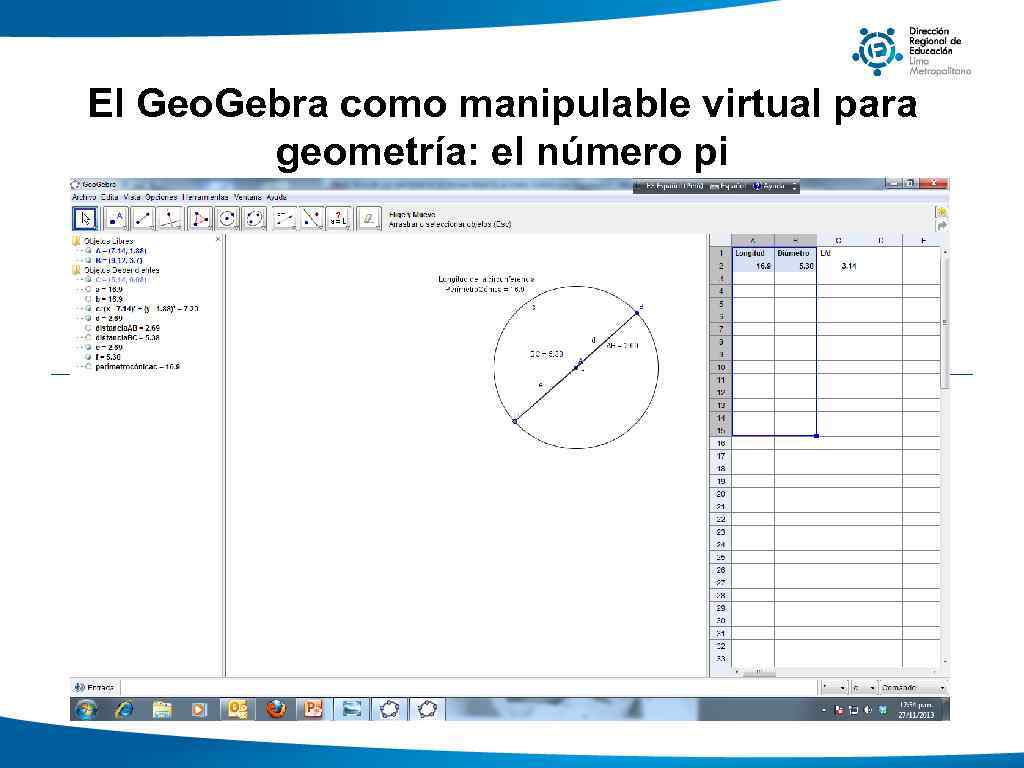El Geo. Gebra como manipulable virtual para geometría: el número pi

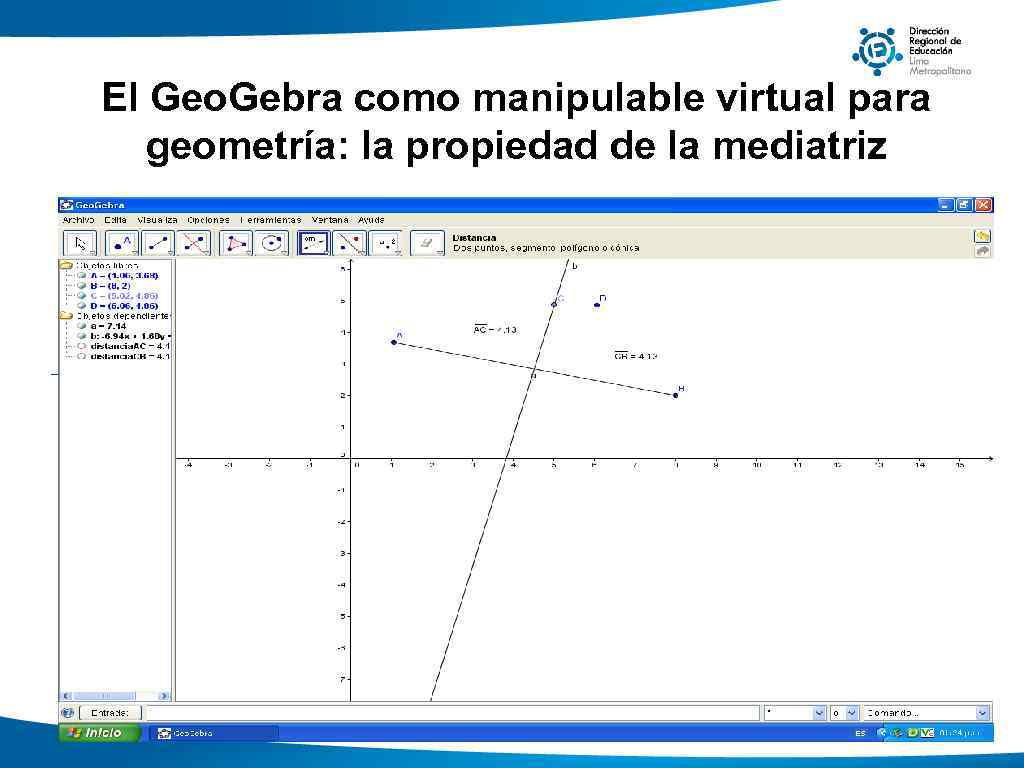El Geo. Gebra como manipulable virtual para geometría: la propiedad de la mediatriz

Función potencia El Graph® como manipulable para trabajar funciones Sesión en cómputo: La sesión se desarrollará en el laboratorio de informática usando el programa Graph. Actividades: Tipo INICIO: motivación, recuperación de saberes previos y conflicto cognitivo. Los alumnos y alumnas repasan Lo que has aprendido. ELABORACIÓN Tiempo 10’ Tiempo T Se explica el uso del Graph: diseño de los ejes; insertar una función; color de la gráfica. 10’ I Realizan las tareas señaladas en el Anexo sesión 9 -Graph. 50’ Tipo CIERRE: sistematización, resumen y metacognición. Tiempo T El grado n de la función determina la forma de la curva, para analizar la monotonía de la función; su simetría; de ser el caso su vértice y sus asíntotas; y, su dominio y su rango, es necesario analizar los parámetros: a; d y e. Si a = 1; d = 0 y e = 0 tenemos las funciones de la forma f(x) = xn. 10’

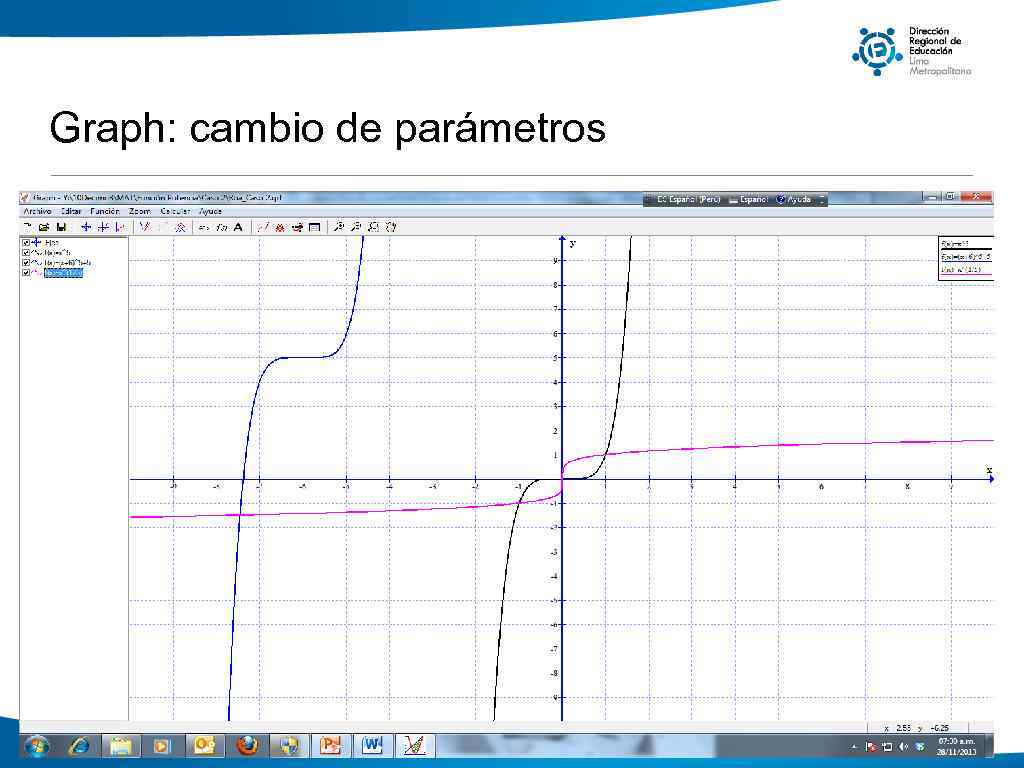Graph: cambio de parámetros

Descartes: el caso de las rectas notables http: //descartes. cnice. mec. es/materiales_didacti cos/rectasnotables/rnotables 0. htm

Descartes: el caso de las áreas sombreadas http: //descartes. cnice. mec. es/descartes 2/previas_web/materiale s_didacticos/areas_regiones_sombreadas/areas_intro. htm

Lo importante no es el manipulable en sí, Sino para qué se usa: - Para descubrir - Para realizar conjeturas - Para preguntar y argumentar - Para analizar opciones - Para enfrentar el conflicto cognitivo o el error constructivo

Utilizar otras alternativas Proyectos Aprendizaje basado en problemas (ABP) Webquests Trabajos cooperativos

Un ejemplo: El álgebra ¿Por qué hemos escogido el álgebra? Es aparentemente el más mecánico de los aprendizajes ….

¿Por qué cuesta aprender álgebra? ¿Qué implica dominar el álgebra? ¿Cómo promover el pensamiento algebraico y cuándo? ¿Por qué es importante? No solo se trata de adquirir destrezas operativas nuevas. Se requiere construir el sentido del álgebra: pensamiento para generalizar, manejar lo desconocido y variable, aplicación de lo inverso para resolver

Dificultades para aprender álgebra Conceptos nuevos Convenciones nuevas Poder describir un proceso no es lo mismo que poder simbolizarlo Falta de dominio de prerrequisitos Necesidad de abstracción (para descubrir patrones y generalizar)

Idea de variable Solución no solo como final de un procedimiento Existencia de restricciones Simbología nueva (letras) o contradictoria (signos = y – se usan diferente), que requiere de comprensión de leyes para su uso (Jerarquía de operaciones y uso de paréntesis) Concatenar ya no es sumar como en 2 1/4 sino multiplicar como en 3 xy

Trabajo de prevención en primaria Signo igual no solo para el resultado, no siempre unidireccional (armar parejas) Respetar el significado del signo igual y no escribir cadenas de operaciones para resolver problemas (perdí 15 y luego 23 por ejemplo): 100 -15 = 85 -23 = 62 Mejor hacia abajo: 100 – 15 – 23 85 – 23

Trabajo de prevención en primaria No siempre pedir respuestas, sino el procedimiento ( + 5 ) Usar sustitución y tanteo para verificar Simbolizar procedimientos con operaciones combinadas. Conocer jerarquía y uso de ( ) Dominio de operaciones; inversas y propiedades, familia de operaciones: 3 + 7 = 10 implica 3 = 10 – 7

Construir el sentido - Modelar la realidad, simbolizar, verificar o buscar soluciones - Generalizar, establecer patrones - Comprender la variación (variables y dependencia de variables)

Tantos ejercicios y “fórmulas” no ayudan a construir el sentido Los alumnos aún están comprendiendo la dinámica del álgebra y se quiere que mejoren en esto antes que mecanizar procedimientos. Se prefiere incluir también ejercicios con diferentes perspectivas para promover el razonamiento (ejercitación inteligente).

Aproximaciones didácticas En esta línea vamos a desarrollar tres vías didácticas para afrontar situaciones algebraicas de tal manera que las dotemos de sentido.

1. - El uso de la geometría para visualizar y comprender Ejemplo: el producto de binomios La interpretación geométrica como una forma de fomentar la comprensión y evitar la algoritmización de la práctica algebraica.

La entrada geométrica Si tenemos un rectángulo de lados a + b y c +d, ¿cuál es su área? Su área es: (a + b) ( c + d) La representamos en una hoja de papel:

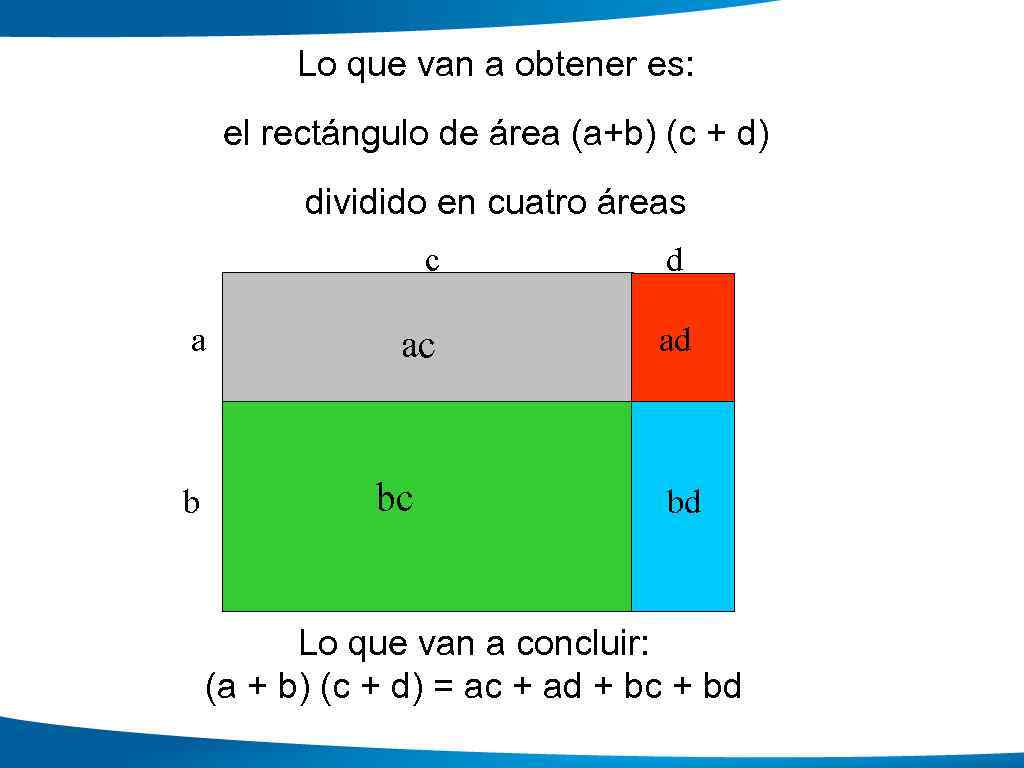Lo que van a obtener es: el rectángulo de área (a+b) (c + d) dividido en cuatro áreas c a b d ac ad bc bd Lo que van a concluir: (a + b) (c + d) = ac + ad + bc + bd

La multiplicación de adiciones por adiciones en MPT Este proceso está en el libro de MPT 2 en la Pág. 52:

2. - La entrada funcional La construcción de la idea de dependencia entre dos magnitudes o cantidades que pueden ser expresadas mediante letras es una oportunidad para arribar al concepto de ecuación. Esta entrada sienta bases para la comprensión del concepto de función.

MPT 2 Pág. 150 La entrada funcional: la solución de sistemas de ecuaciones lineales con dos variables

La entrada funcional: el análisis de la situación En primer lugar es importante observar que el análisis de la situación problemática precede al procedimiento algebraico: Entonces podemos plantear preguntas como: “si compramos 1 afiche grande, ¿cuántos afiches pequeños podemos comprar? ”, “si compramos 2 …”

La entrada funcional: la idea de dependencia La idea es que constatar que existe una relación de dependencia entre las dos variables. Es decir el número de afiches pequeños depende del número de afiches grandes. Esta es la situación que vamos a representar.

La entrada funcional: la necesidad de representación y las ecuaciones Al representar la situación aparece la ecuación que se puede plantear de diversas maneras: p= (32 – 8 g)/4 (que representa mejor el proceso de solución que hemos descrito) o 4 p + 8 g = 32 (que es la tendencia del que conoce más el álgebra)

Los valores que verifican la ecuación Para establecer los valores se puede hacer una tabla, tomar pares ordenados, establecer ejes y darle una interpretación gráfica a la ecuación. Esto permite la comprensión de por qué dos ecuaciones lineales con dos variables pueden tener infinitas soluciones en común, exactamente una solución en común o ninguna solución en común. Aporta un método gráfico de solución de sistemas de ecuaciones lineales con dos variables.

Algunas conclusiones importantes üVarias ecuaciones reflejan la situación problemática. üEn cada ecuación varios valores de la variable o variables la verifican. üNo todos los valores que verifican la ecuación solucionan la situación planteada. La importancia del conjunto de definición. üSe puede establecer la equivalencia de las ecuaciones. El sentido de la simplificación procedimiento algebraica

La idea de dependencia y la idea de función Dado que existe una relación entre un valor y otro que depende de él. Se puede decir que un valor es función del otro. Si p depende de g. p es función de g Puede empezarse a notar que el valor de una variable se decide y el valor de la otra se calcula, una es independiente y la otra dependiente.

3. - La modelización Modelizar una situación matemática: otra oportunidad para arribar al concepto de expresión algebraica. Esta entrada permite insistir en la idea que un solo modelo puede representar distintas situaciones y existen varias formas de modelizar una misma situación.

El álgebra como vía de generalización y de comprobación Esta entrada considera que la modelización es un proceso que permite encontrar “características que unifican, reconocer tipos de objetos y problemas”. La idea de usar la modelización como vía de entrada al álgebra es pensar en su uso para expresar situaciones generales y al mismo tiempo como un mecanismo de validación de conjeturas originadas en reglas de transformación de textos escritos.

La modelización La producción de fórmulas para contar colecciones como una primera experiencia con el lenguaje algebraico.

Ejemplo: cantidad de rectas Determinar la cantidad de rectas que pasan por n puntos tales que ningún trío de ellos sean colineales. Espero propuestas que me permitan resolver la situación planteada

Una primera exploración Una buena manera de aproximarse es explorar casos particulares: 1) 2 puntos – 1 recta 2) 3 puntos – 3 rectas 3) 4 puntos – 6 rectas 4) 5 puntos – 10 rectas … para buscar el patrón que permita establecer la fórmula solicitada

Dos alternativas De cada punto se pueda trazar n – 1 rectas. Hay n puntos Entonces el número de rectas en n (n-1) Pero estamos contando dos veces cada recta, entonces: n(n-1)/2 Otra alternativa: Es el número de lados más el número de diagonales: n + n(n-3)/2

Algunas conclusiones Una situación puede ser representada por diversas expresiones. Las expresiones son equivalentes, lo que puede demostrarse mediante simplificaciones algebraicas.

Algunas notas didácticas Las mismas estrategias que ya vimos: situaciones concretas, representar, verbalizar, interactuar, avance en espiral ejercitación razonada…. . Es importante abordar el tema con los alumnos y alumnas pauteando algunas etapas: Primera: que los alumnos y alumnas comprendan de qué se trata la situación, para lo cuál suele ser útil que recurran a estrategias sencillas como el conteo. Segunda: que los alumnos y alumnas tomen conciencia del límite de ese procedimiento. Tercera: trabajo grupal que permita verbalizar, intercambiar ideas, argumentar, comprobar, valorar diversos puntos de vista.

Para terminar….

Retroalimentación adecuada para mejorar el aprendizaje: Intervención en clase, revisión de cuadernos, resolución de tareas y otras. . . Tiempo para preguntar, aplicar, comparar soluciones…. vamos conociendo qué aprenden y qué no (calificar no es lo único que importa, ni lo más importante).

¿Qué es una buena retroalimentación? üEs aquella que informa claramente el fondo de las dificultades que subsisten y las posibles causas. üPuede usarse códigos para la autocorrección u otros. üRecomienda en consecuencia con lo anterior y no solo generalidades. üReconoce el progreso (no solamente) üReconoce el esfuerzo (no solamente) üVolverle a decir a un alumno con déficit de atención que se distrajo ¿ayuda? üLa calificación sola no es motivación. Necesitamos que se generen sentimientos positivos al respecto, siempre en busca de la motivación intrínseca.

La motivación y el vínculo "Se da gran importancia a la elección de los mejores métodos para aprender a leer; se inventan escritorios, mapas; se convierte la habitación del niño en una imprenta. Locke quiere que aprenda a leer con dados. Qué ingenioso invento, ¿verdad? ¡Qué lástima! Y siempre se olvida el medio más seguro de todos, el deseo de aprender. Dad al niño ese deseo y dejad vuestros escritorios y vuestros dados; cualquier método será eficaz“ El Emilio, J. J. Rousseau http: //www. youtube. com/watch? v=t 5 m. Ge. R 4 AQd. M

…otras voces X: AREASMatemáticaPresentacionesAniversario MPTNuevo. Video