Dictionary-Based Compression Dictionary-Based Compression n n This

Dictionary-Based Compression

Dictionary-Based Compression n n This family of algorithm does not encode single symbols as bit streams, instead they encode phrasees of variable length as single tokens Example : We use the Random House Dictionary of the English Language, 2 nd Ed, Unabridged ‘A good example of how dictionary based compression…. ’ 1/1 822/3 674/4 1343/60 928/75 550/32 173/46 421/2

Dictionary-Based Compression n n There about 31, 5000 words in the dictionary. And thus, by Shannon’s formula for information contents, any one of the words in the dictionary can be encoded using just a little over 18 bits Dictionary-based compression techniques are presently the most popular forms of compression in the lossless area n Winzip

Sliding Window Compression n LZ 77 ( 1977 by Ziv and Lempel ) compression uses previously seen text as a dictionary It replaces phrase in the input text with pointers into the dictionary to achieve compression Example: C program Normal size of the text window : Several thousand chars Normal size of the look-ahead buffer : 10 ~100 chars text window : recently encoded text look ahead buffer : those to be encoded

Sliding Window Compression n Token n n an offset to a phrase in the text window the length of the phrase the first symbol in the look-ahead buffer that follows the phrase A token defines a phrase of variable length in the current look ahead buffer “<MAX^” is encoded as ( 14, 4, ”^”)

Sliding Window Compression n n Emit the token (14, 4, ”^”), then shift the text window over by 5 characters, which is the width of the phrase just encoded Five new symbols are then read into the look-ahead buffer and the process repeats

Sliding Window Compression n Special case for using phrases that have not yet been encoded to encode existing phrases (15, 3, ’A’), (16, 5, ’D’) (15, 9, ’D’)

Sliding Window Compression n Problem with LZ 77 n Performance bottleneck : When encoding, it has to perform string comparisons against the look-ahead buffer for every position in the text window n I. E. encoding time size of the text window n Decoding time is negligible n (0, 0, c) for no matching n First-match and best-match

Sliding Window Compression n LZSS compression: an improved version of LZ 77 As each phrase passes out of the look-ahead buffer and into the encoded portion of the text window, LZSS adds the phrase to a tree structure, binary search tree The time needed to find the longest matching phrase will no longer be proportional to the product of the window size and the phrase length

Sliding Window Compression n Instead, it will be proportional to the base 2 logarithm of the window size multiplied by the phrase length The savings created by using the tree not only makes the compression size of the algorithm much more efficient, it also encourages experimentation with larger window size LZSS instead uses a single bit as a prefix to every output token to indicate whether it is an offset/ length pair or a single symbol for output

Sliding Window Compression n An example of binary search tree

LZ 78 and LZW n n LZ 78 is proposed by the same authors in 1978 in IEEE Trans. on Information Theory The sliding windows makes LZ 77 algorithm biased toward exploiting recent appearance in the text n n Address of the phone book The size of a phrase that can be matched is limited n Restricted by the size of the look-ahead buffer

LZ 78 and LZW n Under LZ 77, the dictionary of phrases was defined by a fixed window of previously seen text n n Under LZ 78, the dictionary is a potentially unlimited list of previously seen phrases Each LZ 78 token consists of a code that selects a given phrase and a single character that follows the phrase n Unlike LZ 77, the phrase length is not passed since the decoder knows it

LZ 78 and LZW n n Unlike LZ 77, LZ 78 does not have a ready-made window full of text to use as a dictionary It creates a new phrase each time a token is output, and it adds that phrase to the dictionary After the phrase is added, it will be available to the encoder at any time in the future, not just for the next few thousand characters The new phrase, consisting of the dictionary match and the new character, is added to the dictionary

LZ 78 and LZW n The next time that phrase appears, it can be used to build an even longer phrase Input text : “DAD DADA DADDY DADO. . . ” Output phrase Output char Encoded String New phrase Code 0 ‘D‘ “D” (1) 0 ‘A‘ “A” (2) 1 ‘ ‘ “D^” (3) 1 ‘A‘ “DA” (4) 4 ‘ ‘ “DA^” (5) 4 ‘D‘ “DAD” (6) 1 ‘Y‘ “DY “ (7) 0 ‘ ‘ “^“ (8) 6 ‘O‘ “DADO” (9)

LZ 78 and LZW n After just 19 characters have been read in and encoded, the dictionary which is sorted in alphabetical order, looks like the one following 1 2 3 4 5 6 7 8 9 “ D“ “A“ “D^“ “DA” “DA^“ “DAD” “ DY “ “^“ “DADO”

LZ 78 and LZW n n Phrases are conventionally stored in a multiway tree as shown above With a tree like this, matching is just a matter of walking through the tree, traversing a single node of the tree for every character in the phrase If the phrase terminates at a particular node, we have a match If there are more symbols to be matched but we cannot walk down the tree any further, then insert a new descendent node at the node last matched, as a new dictionary phrase

LZ 78 and LZW n n n One negative side effect of LZ 78 not found in LZ 77 is that the decoder has to maintain this tree as well The Unix COMPRESS program, which uses an LZ 78 variant, monitors the compression ratio of the file If the compression ratio ever starts to deteriorate, the dictionary is deleted and the program starts over from scratch

LZ 78 and LZW n n Otherwise, the existing dictionary continues to be used, though no new phrase are added to it This makes the phrase dictionary up to date Note that dictionary-based compression algorithm are inherently adaptive It is adaptive by that the dictionary is adaptive, we select some heuristics to keep the dictionary up to date

LZ 78 and LZW n n In fact, under LZW, the compressor never outputs single character, only phrases To do this, the major change in LZW is to preload the phrase dictionary with single symbol phrases equal to the number of symbols in the alphabet

LZ 78 and LZW n Codes 0 -255 pre-defined as the 256 possible character values Input string: “ WED WE WEB WET. . . ” Characters Input Code Output New code value ad associated string “W” ‘^‘ 256=“^W” “E “ ‘W’ 257=“WE” “D“ ‘E’ 258=“ED” “^“ ‘D’ 259=“D^” “WE” 256 260=“^WE” “^“ ‘E’ 261=“E^“ “WEE” 260 262=“^WEE” “^W” 261 263=“E^W” “EB” 257 264=“WEB” “^“ ‘B‘ 265=“B^“ “WET” 260 266=“^WET” “^” ‘T‘ 267=“T^”

LZ 78 and LZW n n n Decompression One reason for the efficiency of the LZW algorithm is that it does not need to pass the dictionary to the decompressor The table can be built exactly as it was during compression, using the input string as data

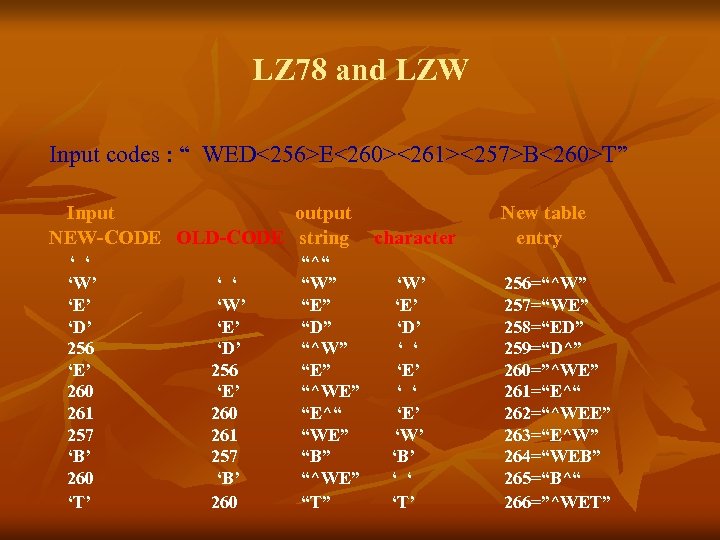
LZ 78 and LZW Input codes : “ WED<256>E<260><261><257>B<260>T” Input output NEW-CODE OLD-CODE string ‘ ‘ ‘W’ ‘E’ ‘D’ 256 ‘E’ 260 261 257 ‘B’ 260 ‘T’ ‘ ‘ ‘W’ ‘E’ ‘D’ 256 ‘E’ 260 261 257 ‘B’ 260 “^“ “W” “E” “D” “^W” “E” “^WE” “E^“ “WE” “B” “^WE” “T” character ‘W’ ‘E’ ‘D’ ‘ ‘ ‘E’ ‘W’ ‘B’ ‘ ‘ ‘T’ New table entry 256=“^W” 257=“WE” 258=“ED” 259=“D^” 260=”^WE” 261=“E^“ 262=“^WEE” 263=“E^W” 264=“WEB” 265=“B^“ 266=”^WET”