8c74d8950d44e238bf5398ad5d8fb0ac.ppt
- Количество слайдов: 56

Dick Bond Inflation & its Cosmic Probes, now & then Cosmic Probes CMB, CMBpol (E, B modes of polarization) B from tensor: Bicep, Planck, Spider, Spud, Ebex, Quiet, Pappa, Clover, …, Bpol CFHTLS SN(192), WL(Apr 07), JDEM/DUNE BAO, LSS, Lya Inflation Then k =(1+q)(a) ~r/16 0< = multi-parameter expansion in (ln. Ha ~ lnk) Dynamics ~ Resolution ~ 10 good e-folds (~10 -4 Mpc-1 to ~ 1 Mpc-1 LSS) ~10+ parameters? Bond, Contaldi, Kofman, Vaudrevange 07 r(kp) i. e. k is prior dependent now, not then. Large (uniform ), Small (uniform ln ). Tiny (roulette inflation of moduli; almost all string-inspired models)

Dick Bond Inflation & its Cosmic Probes, now & then Inflation Now 1+w(a)= sf(a/a eq; as/a eq; zs) goes to a x 3/2 = 3(1+q)/2 ~1 good e-fold. only ~2 params Zhiqi Huang, Bond & Kofman 07 s=0. 0+-0. 25 now, late-inflaton (potential gradient)2 a to +-0. 07 then Planck 1+JDEM SN+DUNE WL, weak s < 0. 3 now <0. 21 then (late-inflaton mass is < Planck mass, but not by a lot) Cosmic Probes Now. CFHTLS SN(192), WL(Apr 07), CMB, BAO, LSS, Lya Cosmic Probes Then JDEM-SN + DUNE-WL + Planck 1

NOW

–Dick Bond Inflation & its Cosmic Probes, now & then Inflation now Dynamical background late-inflaton-field trajectories imprint luminosity distance, angular diameter distance, volume growth, growth rate of density fluctuations Prior late-inflaton primordial fluctuation information is largely lost because tiny mass (field sound speed=c? ) late-inflaton may have an imprint on other fields? New late-inflaton fluctuating field power is tiny
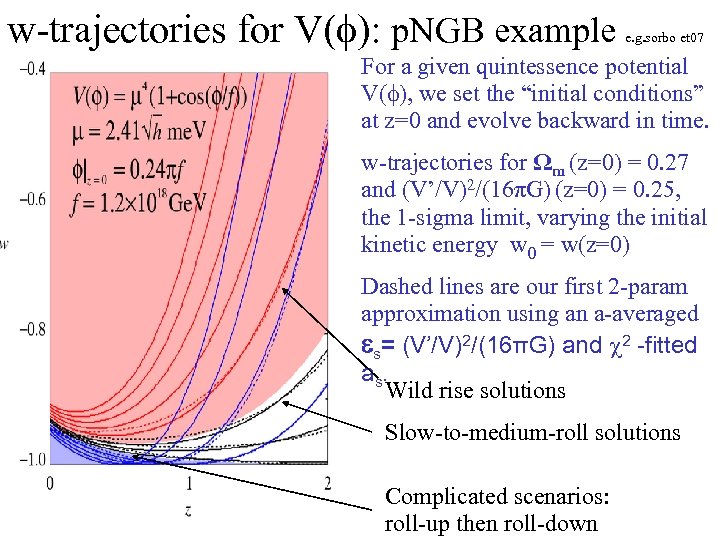
w-trajectories for V(f): p. NGB example e. g. sorbo et 07 For a given quintessence potential V(f), we set the “initial conditions” at z=0 and evolve backward in time. w-trajectories for Ωm (z=0) = 0. 27 and (V’/V)2/(16πG) (z=0) = 0. 25, the 1 -sigma limit, varying the initial kinetic energy w 0 = w(z=0) Dashed lines are our first 2 -param approximation using an a-averaged s= (V’/V)2/(16πG) and c 2 -fitted a s. Wild rise solutions Slow-to-medium-roll solutions Complicated scenarios: roll-up then roll-down

Approximating Quintessence for Phenomenology Zhiqi Huang, Bond & Kofman 07 + Friedmann Equations + DM+B 1+w=2 sin 2 Include a w<-1 phantom field, via a negative kinetic energy term 1+w=-2 sinh 2
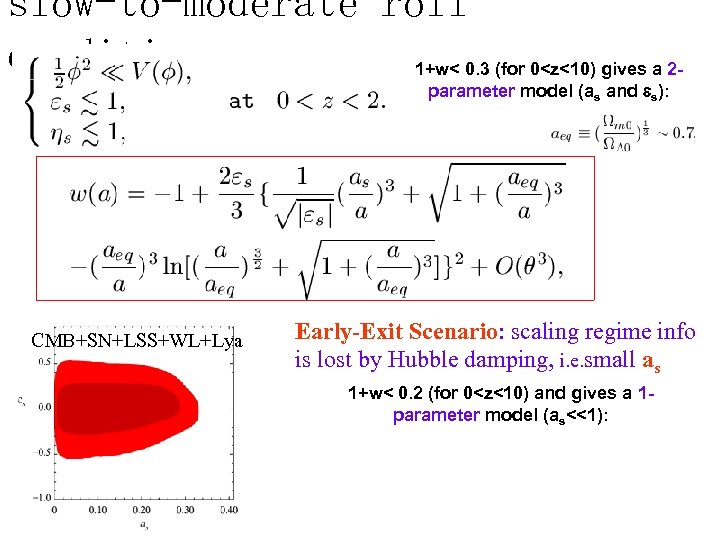
slow-to-moderate roll conditions 1+w< 0. 3 (for 0<z<10) gives a 2 parameter model (as and s): CMB+SN+LSS+WL+Lya Early-Exit Scenario: scaling regime info is lost by Hubble damping, i. e. small as 1+w< 0. 2 (for 0<z<10) and gives a 1 parameter model (as<<1):
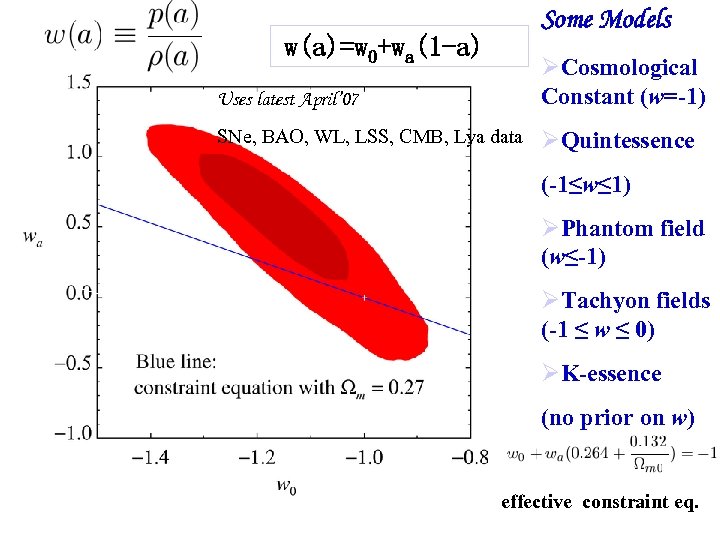
Some Models w(a)=w 0+wa(1 -a) Uses latest April’ 07 Cosmological Constant (w=-1) SNe, BAO, WL, LSS, CMB, Lya data Quintessence (-1≤w≤ 1) Phantom field (w≤-1) Tachyon fields (-1 ≤ w ≤ 0) K-essence (no prior on w) effective constraint eq.
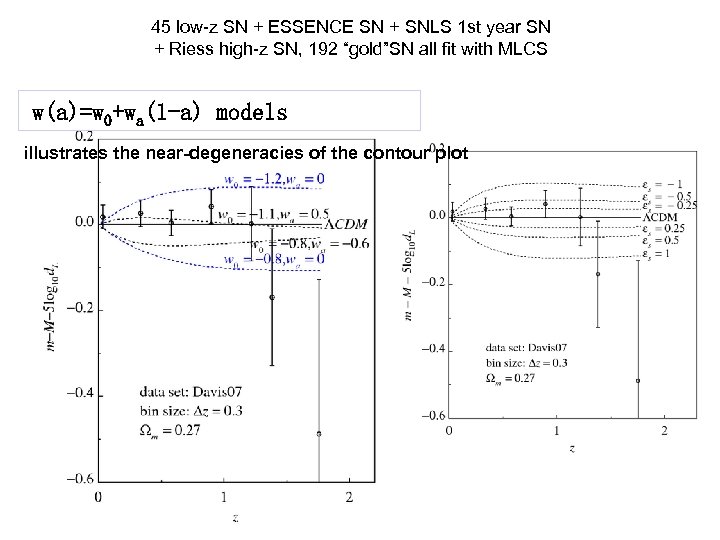
45 low-z SN + ESSENCE SN + SNLS 1 st year SN + Riess high-z SN, 192 “gold”SN all fit with MLCS w(a)=w 0+wa(1 -a) models illustrates the near-degeneracies of the contour plot
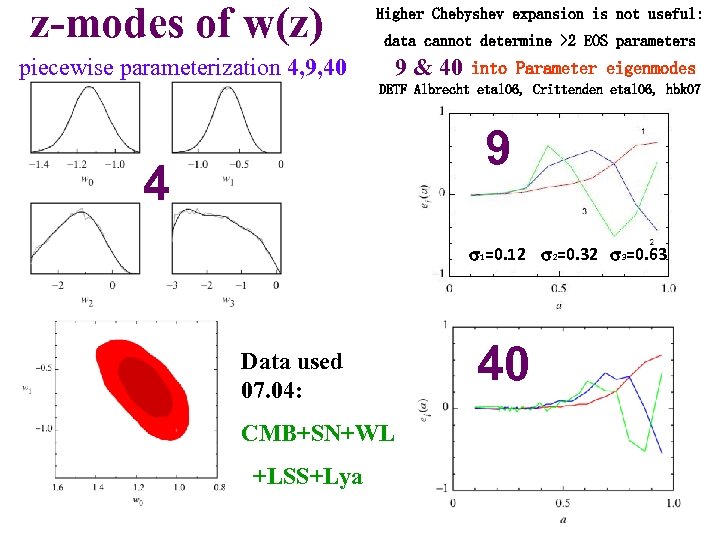
z-modes of w(z) piecewise parameterization 4, 9, 40 Higher Chebyshev expansion is not useful: data cannot determine >2 EOS parameters 9 & 40 into Parameter eigenmodes DETF Albrecht etal 06, Crittenden etal 06, hbk 07 9 4 1=0. 12 2=0. 32 3=0. 63 Data used 07. 04: CMB+SN+WL +LSS+Lya 40
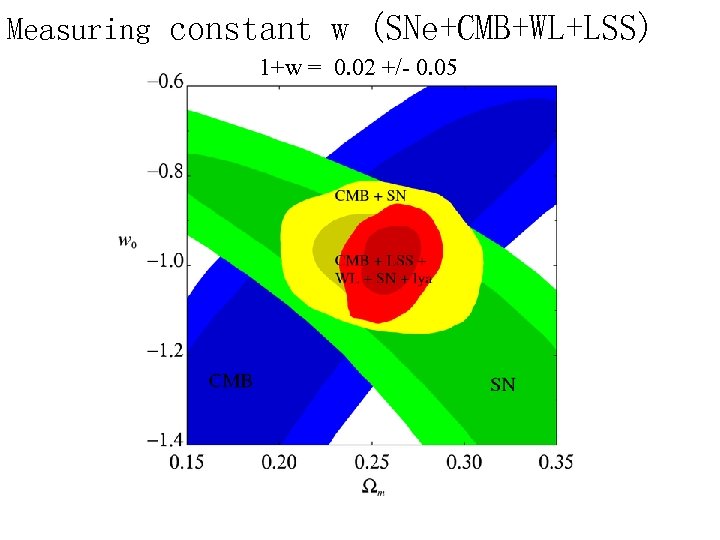
Measuring constant w (SNe+CMB+WL+LSS) 1+w = 0. 02 +/- 0. 05
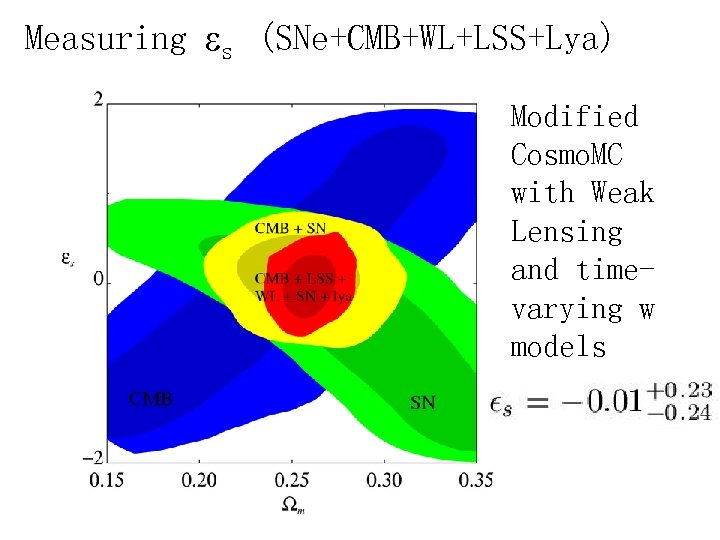
Measuring s (SNe+CMB+WL+LSS+Lya) Modified Cosmo. MC with Weak Lensing and timevarying w models
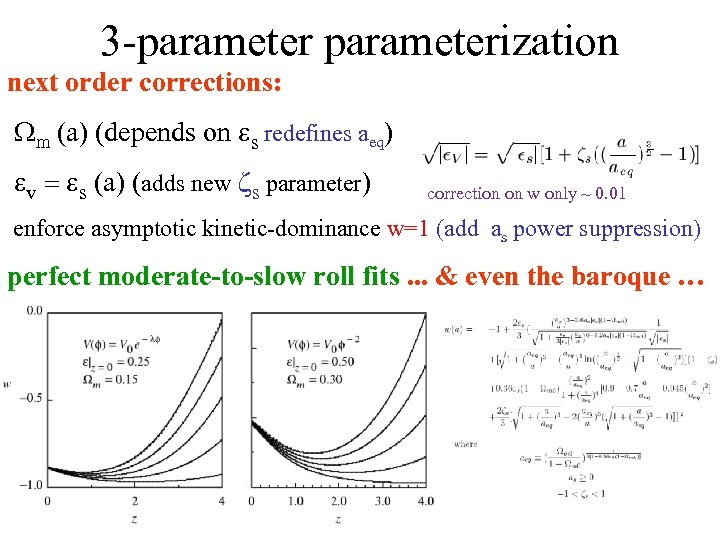
3 -parameterization next order corrections: Wm (a) (depends on s redefines aeq) v = s (a) (adds new zs parameter) correction on w only ~ 0. 01 enforce asymptotic kinetic-dominance w=1 (add as power suppression) perfect moderate-to-slow roll fits. . . & even the baroque …
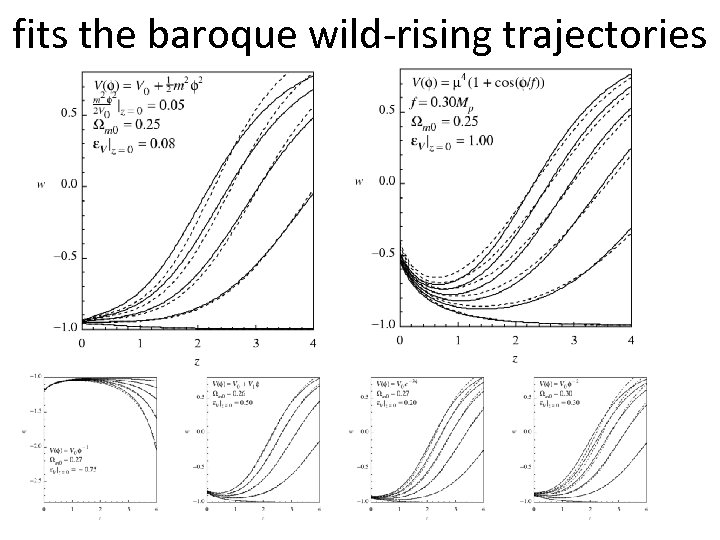
fits the baroque wild-rising trajectories
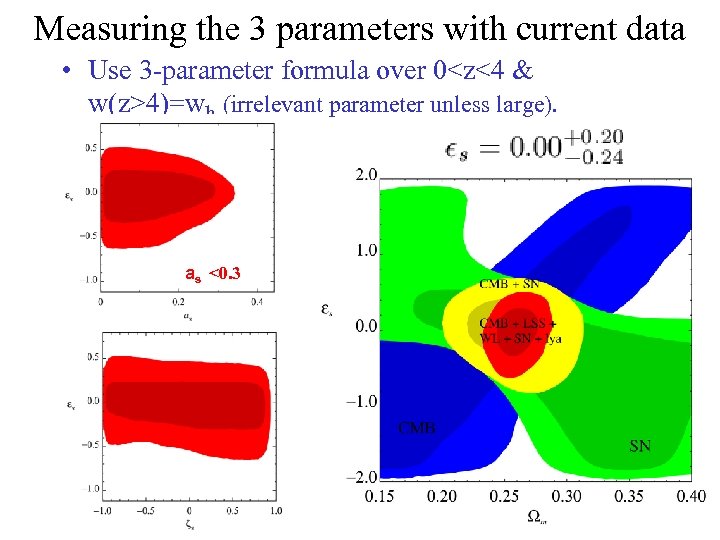
Measuring the 3 parameters with current data • Use 3 -parameter formula over 0<z<4 & w(z>4)=wh (irrelevant parameter unless large). as <0. 3
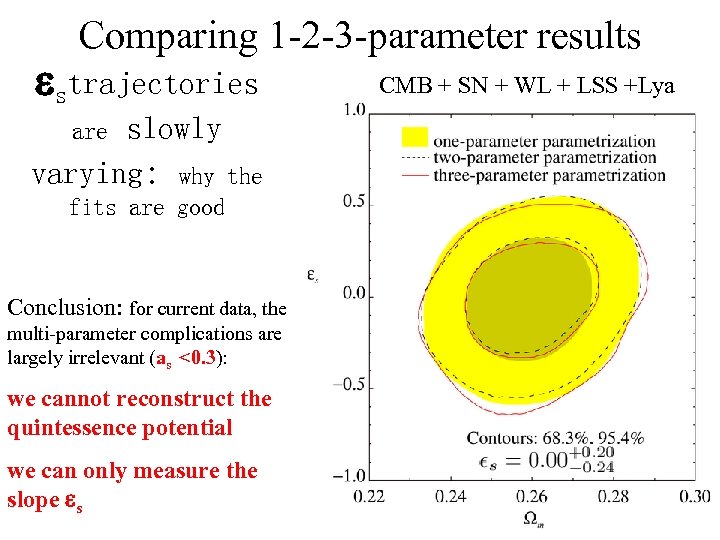
Comparing 1 -2 -3 -parameter results strajectories slowly varying: why the are fits are good Conclusion: for current data, the multi-parameter complications are largely irrelevant (as <0. 3): we cannot reconstruct the quintessence potential we can only measure the slope s CMB + SN + WL + LSS +Lya

Thawing, freezing or non-monotonic? • Thawing: 1+w monotonic up as z decreases • Freezing: 1+w monotonic down to 0 as z decreases • ~15% thaw, 8% freeze, most non-monotonic with flat priors With freezing prior: With thawing prior:
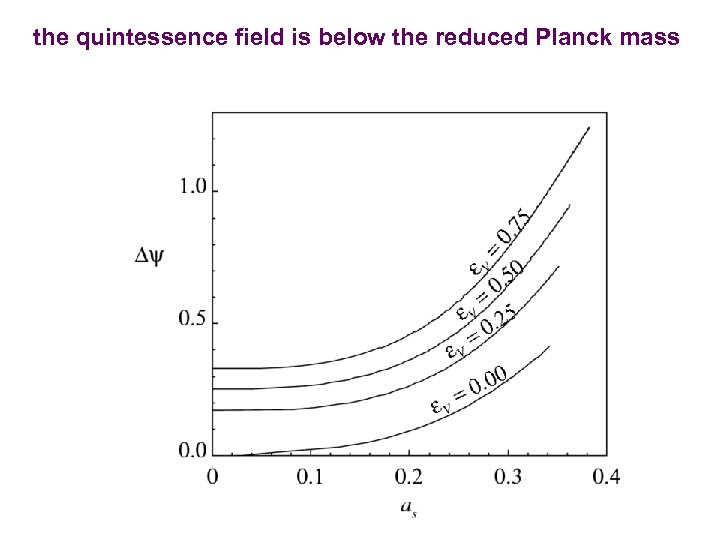
the quintessence field is below the reduced Planck mass
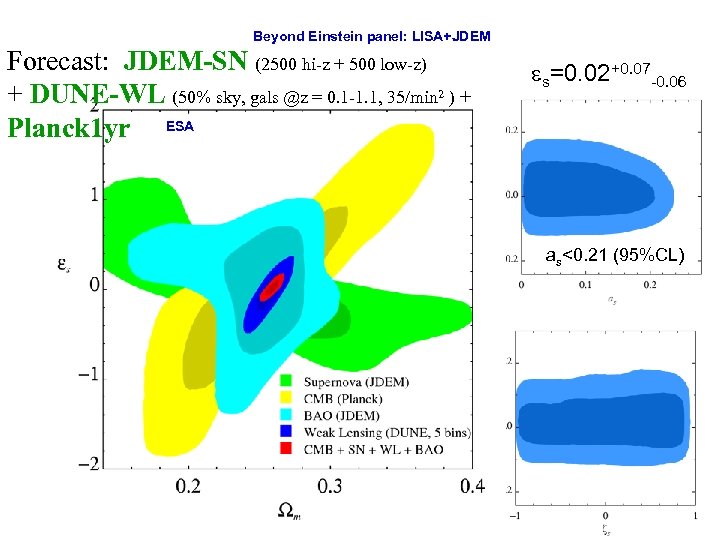
Beyond Einstein panel: LISA+JDEM Forecast: JDEM-SN (2500 hi-z + 500 low-z) + DUNE-WL (50% sky, gals @z = 0. 1 -1. 1, 35/min 2 ) + Planck 1 yr ESA s=0. 02+0. 07 -0. 06 as<0. 21 (95%CL)

Inflation now summary • the data cannot determine more than 2 w-parameters (+ csound? ). general higher order Chebyshev expansion in 1+w as for “inflation-then” =(1+q) is not that useful. Parameter eigenmodes show what is probed • The w(a)=w 0+wa(1 -a) phenomenology requires baroque potentials • Philosophy of HBK 07: backtrack from now (z=0) all w-trajectories arising from quintessence ( s >0) and the phantom equivalent ( s <0); use a 3 -parameter model to well-approximate even rather baroque w • -trajectories. We ignore constraints on Q-density from photon-decoupling and BBN because further trajectory extrapolation is needed. Can include via a prior on WQ (a) at z_dec and z_bbn • For general slow-to-moderate rolling one needs 2 “dynamical parameters” (as, s) & WQ to describe w to a few % for the not-too-baroque w-trajectories. • as is < 0. 3 current data (zs >2. 3) SN+DUNE-WL future to <0. 21 (zs >3. 7) in Planck 1 yr-CMB+JDEM- In the early-exit scenario, the information stored in as is erased by Hubble friction over the observable range & w can be described by a single parameter s. • • • a 3 rd param zs, (~d s /dlna) is ill-determined now & in a Planck 1 yr-CMB+JDEM-SN+DUNE-WL future To use: given V, compute trajectories, do a-averaged s & test (or simpler s -estimate) for each given Q-potential, velocity, amp, shape parameters are needed to define a w-trajectory s=0. 0+-0. 25 • current observations are well-centered around the cosmological constant • • in Planck 1 yr-CMB+JDEM-SN+DUNE-WL future s to +-0. 07 but cannot reconstruct the quintessence potential, just the slope s & hubble drag info • late-inflaton mass is < Planck mass, but not by a lot • Aside: detailed results depend upon the SN data set used. Best available used here (192 SN), soon CFHT SNLS ~300 SN + ~100 non-CFHTLS. will put all on the same analysis/calibration footing – very important. Newest CFHTLS Lensing data is important to narrow the range over just CMB and SN •

THEN

Dick Bond Inflation & its Cosmic Probes, now & then Inflation then Amplitude As, average slope <ns>, slope fluctuations dns = ns -< ns > (running, running of running, …) for scalar (low L to high L CMB ACT/SPT; Epol Quad, SPTpol, Quiet 2, Planck) & tensor At, <nt>, dnt = nt-< nt > (low L <100 Planck, Bicep, EBEX, Spider, SPUD, Clover, Bpol) & isocurvature Ais, <nis>, dnis= nis-< nis> power spectra (subdominant) Blind search for structure (not really blind because of prior probabilities/measures) Fluctuation field power spectra related to dynamical background field trajectories Defines a tensor/scalar functional relation between; both to Hubble & inflaton potential

Standard Parameters of Cosmic Structure Formation Period of inflationary expansion, quantum noise metric perturbations r < 0. 6 or < 0. 28 95% CL Scalar Amplitude Density of Cosmological of index of Density of non. Spectral to index Tensor What is the Background Optical Depth. Amplitude Baryonic Matter Constant scalar tensor interacting Dark primordial curvature of the universe? Last Scattering Matter (compressional) Waves) (Gravity Surface closed perturbationsstars Whenperturbations did flat reionize the open universe?

The Parameters of Cosmic Structure Formation Cosmic Numerology: aph/0611198 – our Acbar paper on the basic 7+; bckv 07 WMAP 3 modified+B 03+CBIcombined+Acbar 06+LSS (SDSS+2 d. F) + DASI (incl polarization and CMB weak lensing and t. SZ) ns =. 958 +-. 015 Wbh 2 =. 0226 +-. 0006 . 93 +-. 03 @0. 05/Mpc run&tensor Wch 2 =. 114 +-. 005 r=At / As < 0. 28 95% CL WL =. 73 +. 02 -. 03 <. 36 CMB+LSS h =. 707 +-. 021 run&tensor dns /dln k = -. 060 +-. 022 Wm =. 27 +. 03 -. 02 -. 038 +-. 024 CMB+LSS run&tensor z = 11. 4 +- 2. 5 reh As = 22 +- 2 x 10 -10
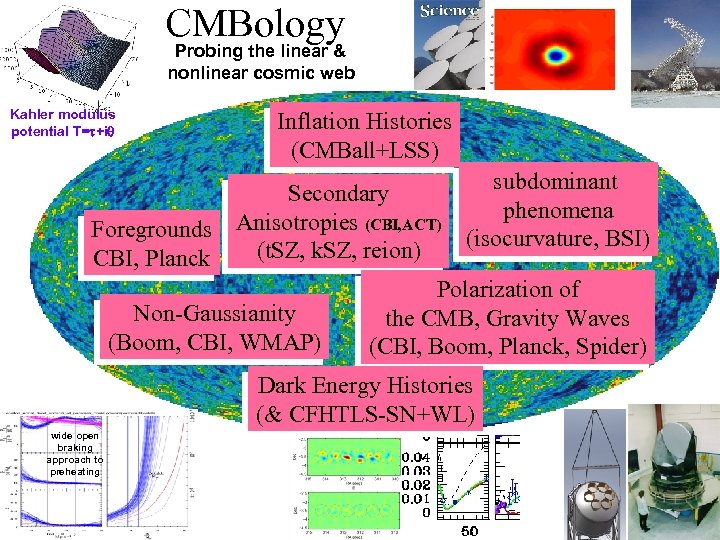
CMBology Probing the linear & nonlinear cosmic web Kahler modulus potential T=t+iq Inflation Histories (CMBall+LSS) subdominant Secondary phenomena Anisotropies (CBI, ACT) Foregrounds (isocurvature, BSI) (t. SZ, k. SZ, reion) CBI, Planck Polarization of Non-Gaussianity the CMB, Gravity Waves (Boom, CBI, WMAP) (CBI, Boom, Planck, Spider) Dark Energy Histories (& CFHTLS-SN+WL) wide open braking approach to preheating
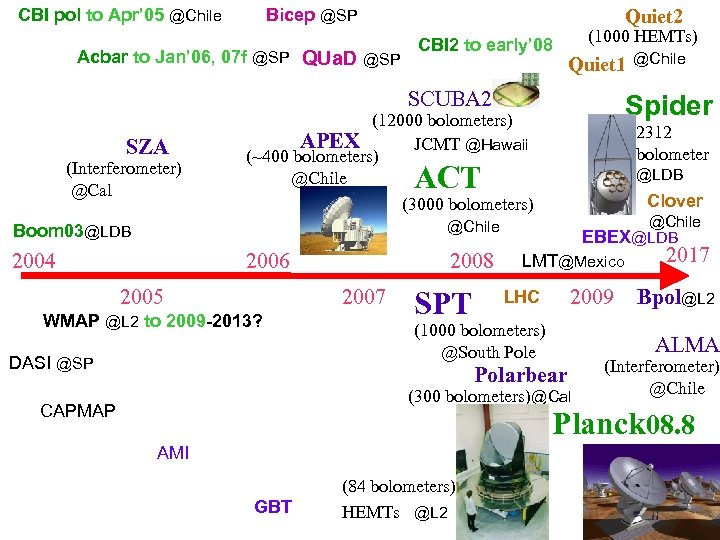
CBI pol to Apr’ 05 @Chile Bicep @SP Acbar to Jan’ 06, 07 f @SP QUa. D @SP Quiet 2 CBI 2 to early’ 08 (1000 HEMTs) Quiet 1 SCUBA 2 SZA (Interferometer) @Cal Spider (12000 bolometers) APEX JCMT @Hawaii (~400 bolometers) @Chile (3000 bolometers) 2312 bolometer ACT @LDB Clover @Chile EBEX@LDB @Chile Boom 03@LDB 2004 2006 2005 2008 2007 WMAP @L 2 to 2009 -2013? DASI @SP SPT LMT@Mexico 2009 LHC (1000 bolometers) @South Pole 2017 Bpol@L 2 ALMA Polarbear (300 bolometers)@Cal CAPMAP @Chile (Interferometer) @Chile Planck 08. 8 AMI GBT (84 bolometers) HEMTs @L 2

ACT@5170 m why Atacama? driest desert in the world. thus: cbi, toco, apex, asti, act, alma, quiet, clover CBI 2@5040 m
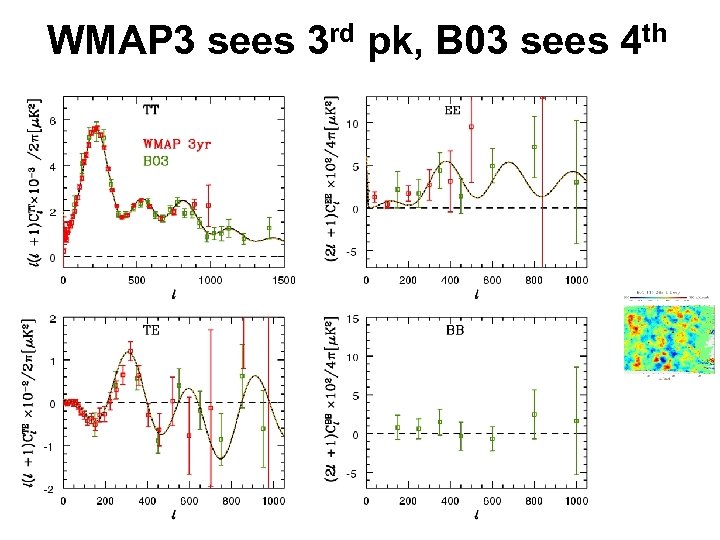
WMAP 3 sees 3 rd pk, B 03 sees 4 th
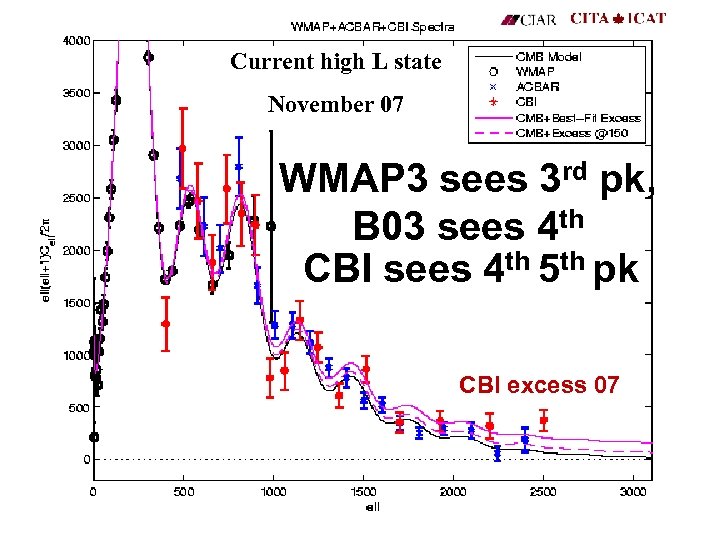
Current high L state November 07 WMAP 3 sees 3 rd pk, B 03 sees 4 th CBI sees 4 th 5 th pk CBI excess 07
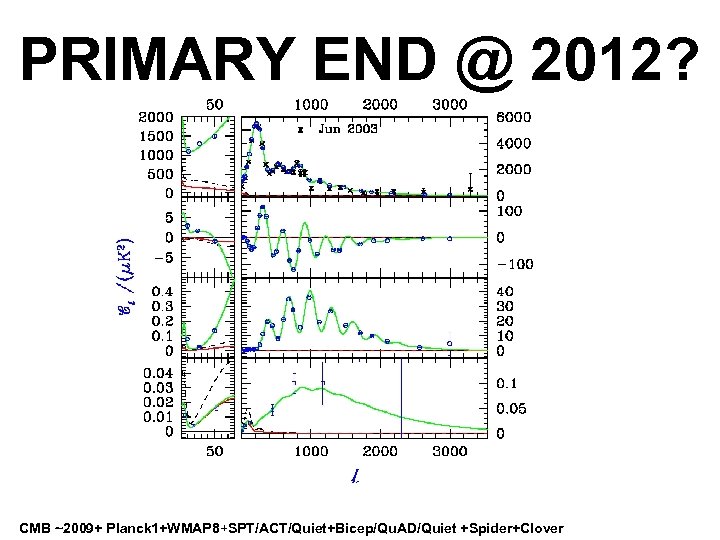
PRIMARY END @ 2012? CMB ~2009+ Planck 1+WMAP 8+SPT/ACT/Quiet+Bicep/Qu. AD/Quiet +Spider+Clover
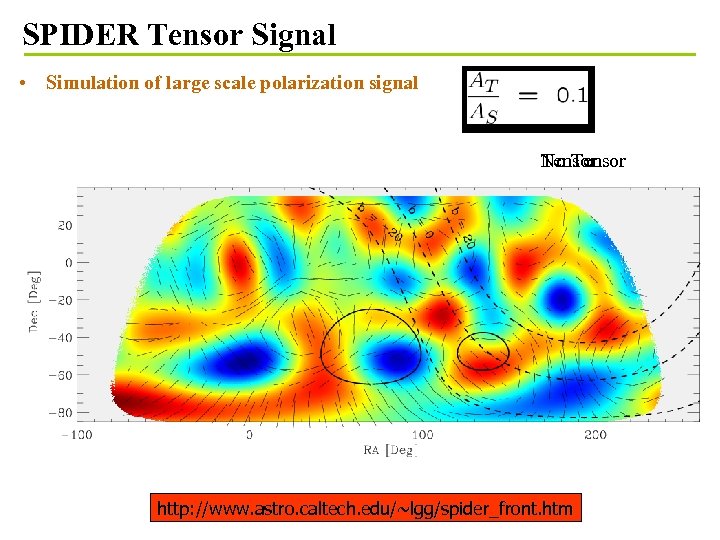
SPIDER Tensor Signal • Simulation of large scale polarization signal Tensor No Tensor http: //www. astro. caltech. edu/~lgg/spider_front. htm
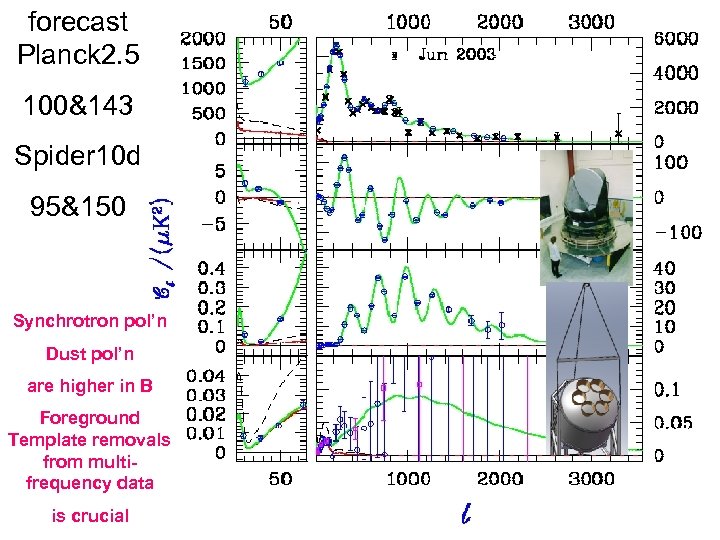
forecast Planck 2. 5 100&143 Spider 10 d 95&150 Synchrotron pol’n Dust pol’n are higher in B Foreground Template removals from multifrequency data is crucial
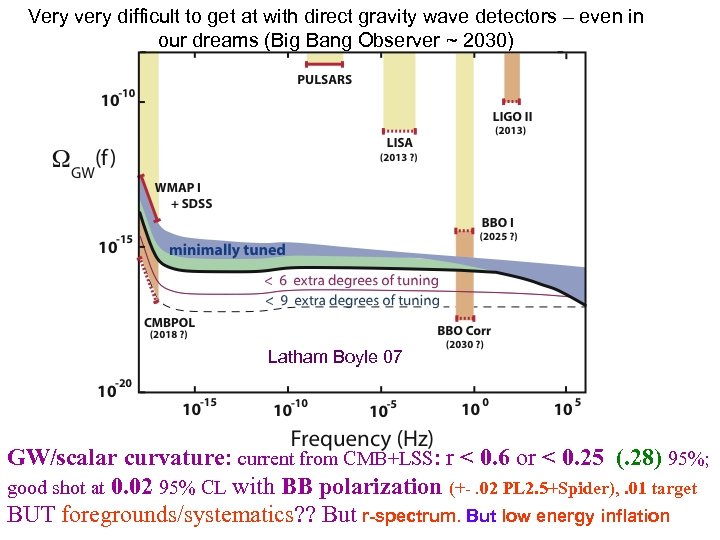
Very very difficult to get at with direct gravity wave detectors – even in our dreams (Big Bang Observer ~ 2030) Latham Boyle 07 GW/scalar curvature: current from CMB+LSS: r < 0. 6 or < 0. 25 (. 28) 95%; good shot at 0. 02 95% CL with BB polarization (+-. 02 PL 2. 5+Spider), . 01 target BUT foregrounds/systematics? ? But r-spectrum. But low energy inflation
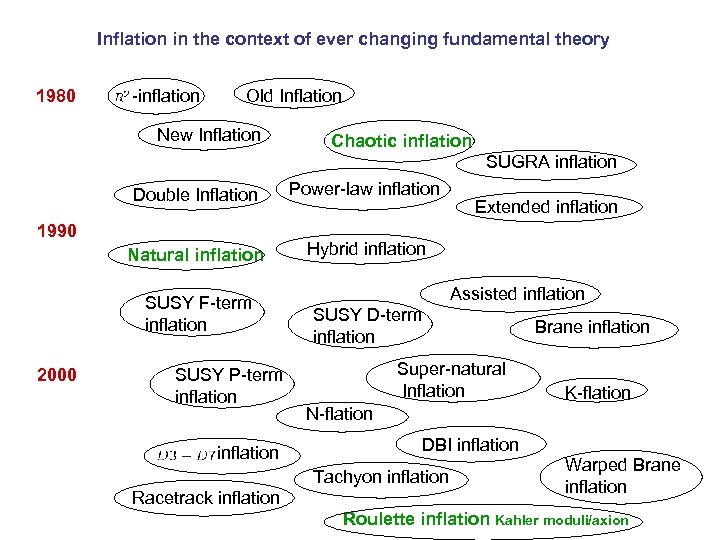
Inflation in the context of ever changing fundamental theory 1980 -inflation Old Inflation New Inflation Chaotic inflation SUGRA inflation Double Inflation Power-law inflation Natural inflation Hybrid inflation 1990 SUSY F-term inflation 2000 SUSY P-term inflation Assisted inflation SUSY D-term inflation Brane inflation Super-natural Inflation K-flation N-flation DBI inflation Tachyon inflation Racetrack inflation Extended inflation Warped Brane inflation Roulette inflation Kahler moduli/axion

Power law (chaotic) potentials 4 ~ l y 2 n , y=f/M 2 V/MP P -1/2 = n/y 2 , = n/2 / NI(k) +n/3 , ns-1= - n+1 / NI(k) -n/6 , nt= - n/ NI(k) -n/6 , n=1, NI ~ 60, r = 0. 3, ns=. 967, nt= -. 0 7 n=2, NI ~ 60, r = 0. 26, ns=. 950, nt= -. 034 MP-2= 8 p. G
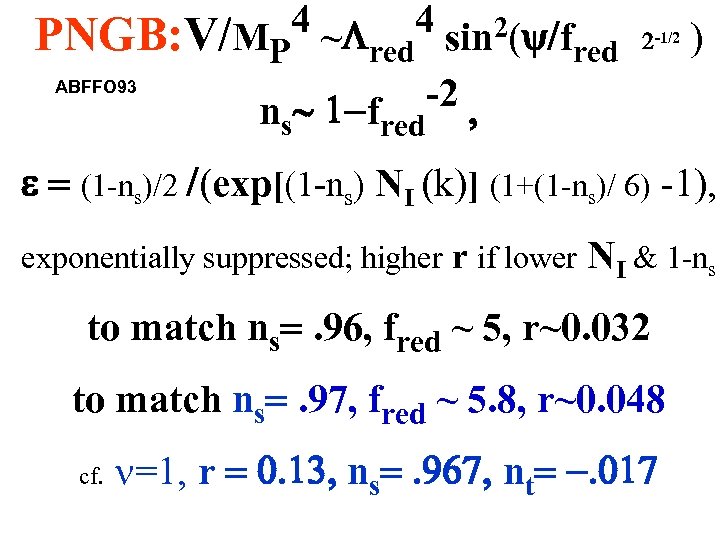
4 ~L 4 sin 2 y/f PNGB: V/MP red ABFFO 93 -2 , n ~ -f s 2 -1/2 red = 1 -ns /2 / exp[ 1 -ns NI (k)] (1+ 1 -ns / 6 -1 , exponentially suppressed; higher r if lower NI & 1 -ns to match ns=. 96, fred ~ 5, r~0. 032 to match ns=. 97, fred ~ 5. 8, r~0. 048 cf. n=1, r = 0. 3, ns=. 967, nt= -. 0 7

Moduli/brane distance limitation in stringy inflation. Normalized canonical inflaton Dy over DN ~ 50, e. g. 2/nbrane 1/2 BM 06 2 so r = 6 <. 007, <<? = (dy /d ln a) roulette inflation examples r ~ 10 -10 & Dy . 002 possible way out with many fields assisting: N-flation ns=. 97, fred ~ 5. 8, r~0. 048, Dy ~ 3 cf. n=1, r = 0. 3, ns=. 967, Dy ~ 0 n=2, r = 0. 26, ns=. 95, Dy ~ 6

energy scale of inflation & r 4 ~ P r (1 - /3) 3/2 V/MP s V~ (1016 Gev)4 r/0. 1 (1 - /3) roulette inflation examples V~ (few x 1013 Gev)4 H/MP ~ 10 -5 (r/. 1)1/2 inflation energy scale cf. the gravitino mass (Kallosh & Linde 07) if a KKLT/large. VCY-like generation mechanism 1013 Gev (r/. 01)1/2 ~ H < m 3/2 cf. ~Tev
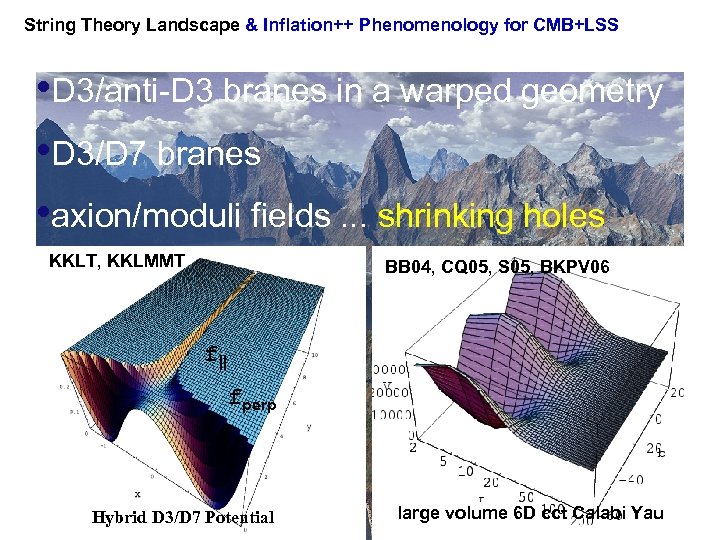
String Theory Landscape & Inflation++ Phenomenology for CMB+LSS • D 3/anti-D 3 branes in a warped geometry • D 3/D 7 branes • axion/moduli fields. . . shrinking holes KKLT, KKLMMT BB 04, CQ 05, S 05, BKPV 06 f|| fperp Hybrid D 3/D 7 Potential large volume 6 D cct Calabi Yau
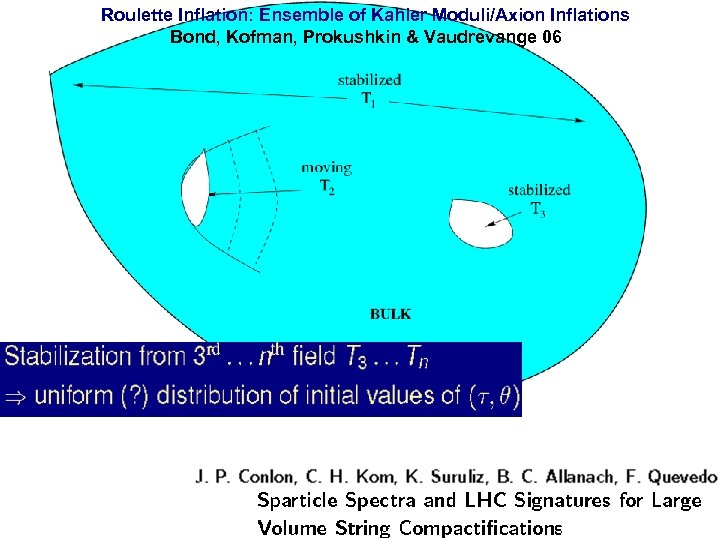
Roulette Inflation: Ensemble of Kahler Moduli/Axion Inflations Bond, Kofman, Prokushkin & Vaudrevange 06 end
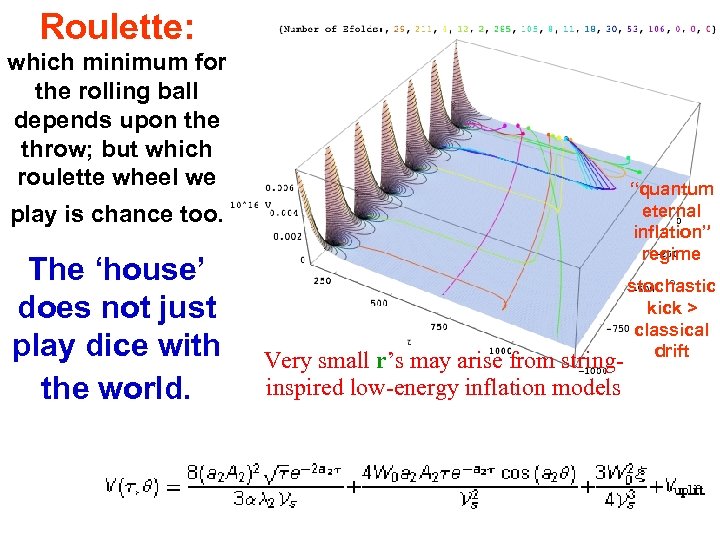
Roulette: which minimum for the rolling ball depends upon the throw; but which roulette wheel we “quantum eternal inflation” regime play is chance too. The ‘house’ does not just play dice with the world. Very small r’s may arise from stringinspired low-energy inflation models stochastic kick > classical drift
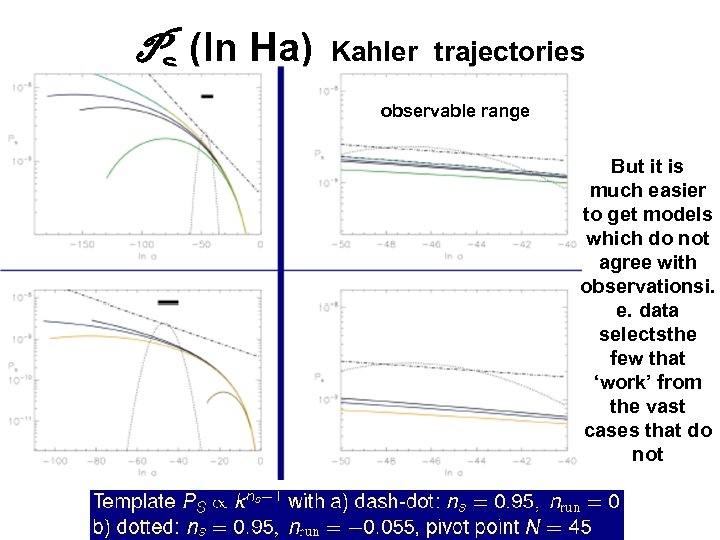
Ps (ln Ha) Kahler trajectories observable range But it is much easier to get models which do not agree with observationsi. e. data selectsthe few that ‘work’ from the vast cases that do not
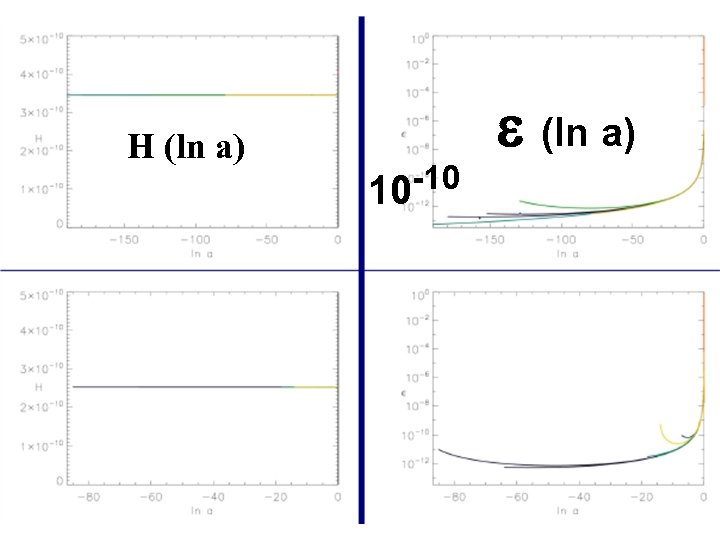
H (ln a) -10 10

New Parameters of Cosmic Structure Formation scalar spectrum use order N Chebyshev expansion in ln k, N-1 parameters amplitude(1), tilt(2), running(3), … (or N-1 nodal point klocalized values) tensor (GW) spectrum use order M Chebyshev expansion in ln k, M-1 parameters amplitude(1), tilt(2), running(3), . . . Dual Chebyshev expansion in ln k: Standard 6 is Cheb=2 Standard 7 is Cheb=2, Cheb=1 Run is Cheb=3 Run & tensor is Cheb=3, Cheb=1 Low order N, M power law but high order Chebyshev is Fourier-like
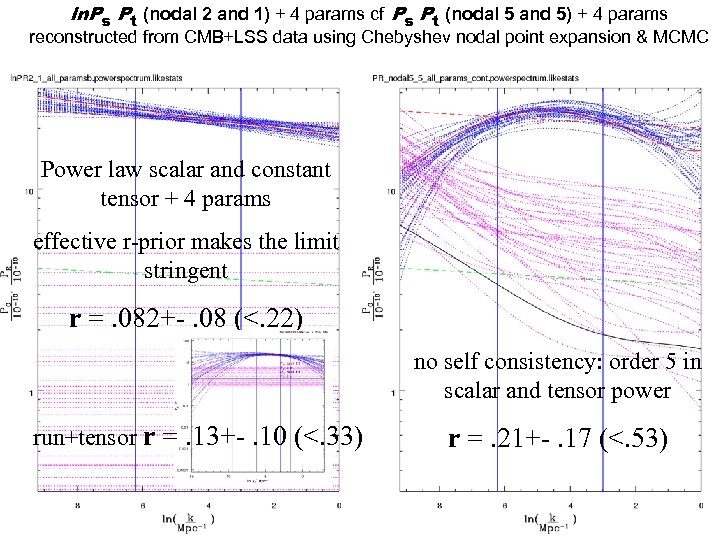
ln. Ps Pt (nodal 2 and 1) + 4 params cf Ps Pt (nodal 5 and 5) + 4 params reconstructed from CMB+LSS data using Chebyshev nodal point expansion & MCMC Power law scalar and constant tensor + 4 params effective r-prior makes the limit stringent r =. 082+-. 08 (<. 22) no self consistency: order 5 in scalar and tensor power run+tensor r =. 13+-. 10 (<. 33) r =. 21+-. 17 (<. 53)
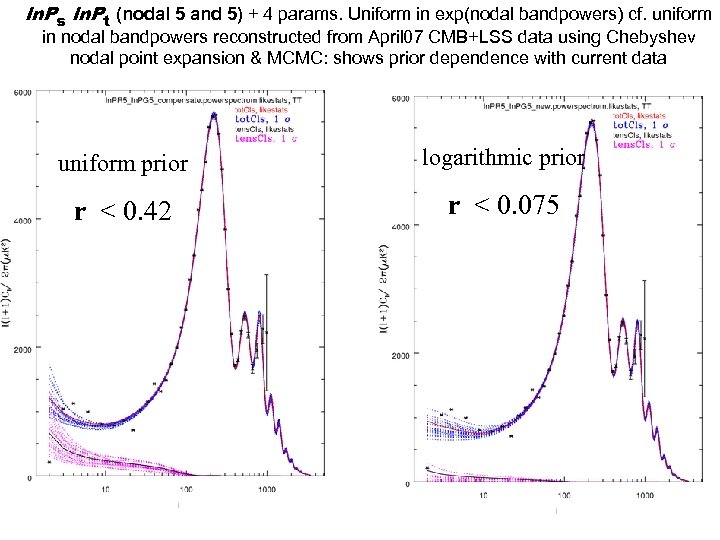
ln. Ps ln. Pt (nodal 5 and 5) + 4 params. Uniform in exp(nodal bandpowers) cf. uniform in nodal bandpowers reconstructed from April 07 CMB+LSS data using Chebyshev nodal point expansion & MCMC: shows prior dependence with current data uniform prior logarithmic prior r < 0. 42 r < 0. 075

New Parameters of Cosmic Structure Formation Hubble parameter at inflation at a pivot pt =1+q, the deceleration parameter history order N Chebyshev expansion, N-1 parameters (e. g. nodal point values) Fluctuations are from stochastic kicks ~ H/2 p superposed on the downward drift at Dlnk=1. Potential trajectory from HJ (SB 90, 91):
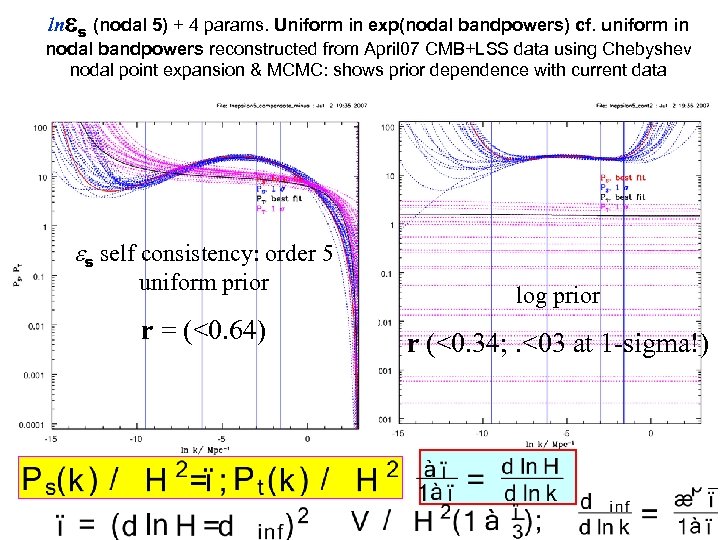
ln s (nodal 5) + 4 params. Uniform in exp(nodal bandpowers) cf. uniform in nodal bandpowers reconstructed from April 07 CMB+LSS data using Chebyshev nodal point expansion & MCMC: shows prior dependence with current data es self consistency: order 5 uniform prior r = (<0. 64) log prior r (<0. 34; . <03 at 1 -sigma!)
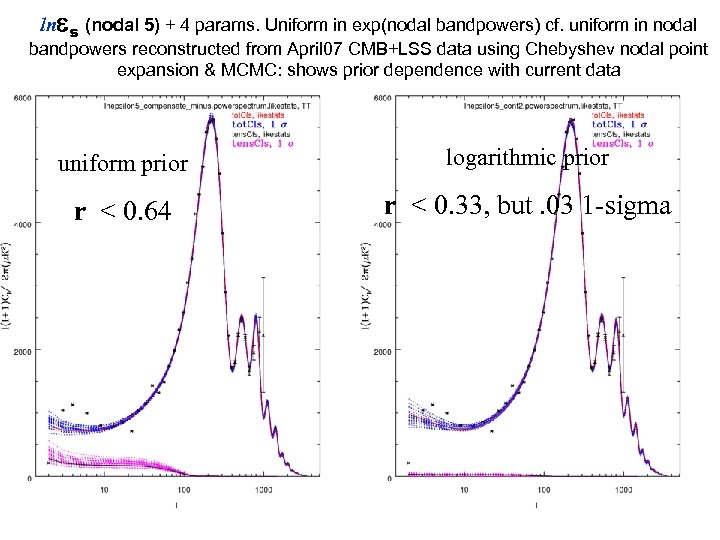
ln s (nodal 5) + 4 params. Uniform in exp(nodal bandpowers) cf. uniform in nodal bandpowers reconstructed from April 07 CMB+LSS data using Chebyshev nodal point expansion & MCMC: shows prior dependence with current data uniform prior logarithmic prior r < 0. 64 r < 0. 33, but. 03 1 -sigma
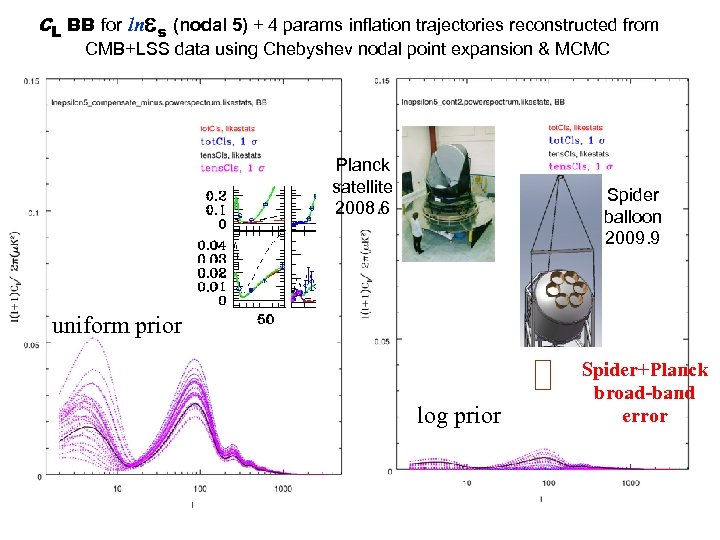
CL BB for ln s (nodal 5) + 4 params inflation trajectories reconstructed from CMB+LSS data using Chebyshev nodal point expansion & MCMC Planck satellite 2008. 6 Spider balloon 2009. 9 uniform prior log prior Spider+Planck broad-band error
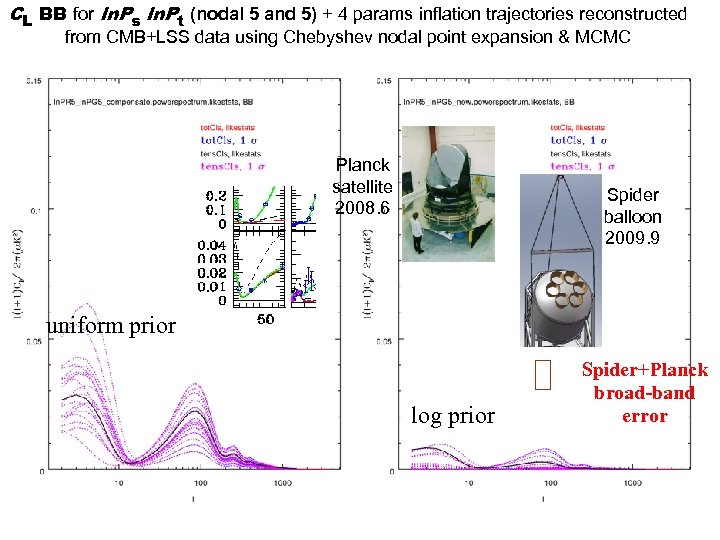
CL BB for ln. Ps ln. Pt (nodal 5 and 5) + 4 params inflation trajectories reconstructed from CMB+LSS data using Chebyshev nodal point expansion & MCMC Planck satellite 2008. 6 Spider balloon 2009. 9 uniform prior log prior Spider+Planck broad-band error
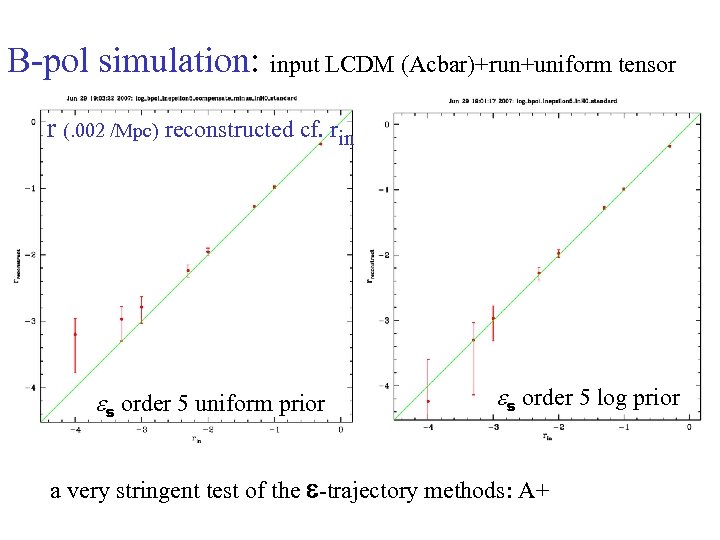
B-pol simulation: input LCDM (Acbar)+run+uniform tensor r (. 002 /Mpc) reconstructed cf. rin es order 5 uniform prior es order 5 log prior a very stringent test of the -trajectory methods: A+
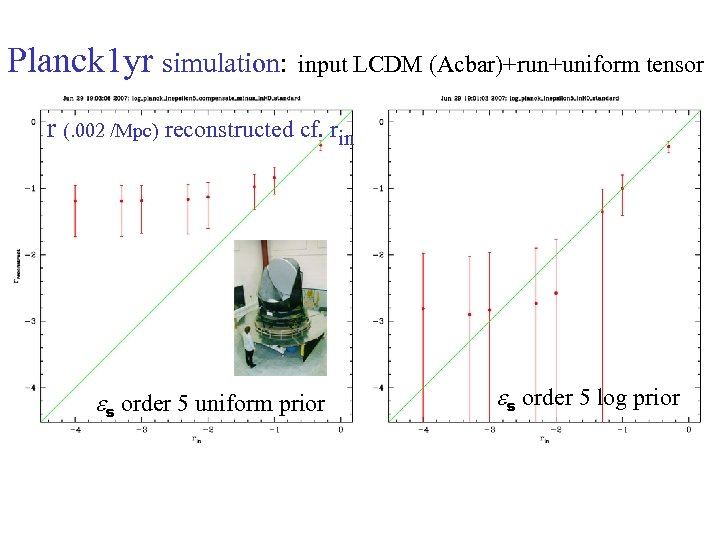
Planck 1 yr simulation: input LCDM (Acbar)+run+uniform tensor r (. 002 /Mpc) reconstructed cf. rin es order 5 uniform prior es order 5 log prior
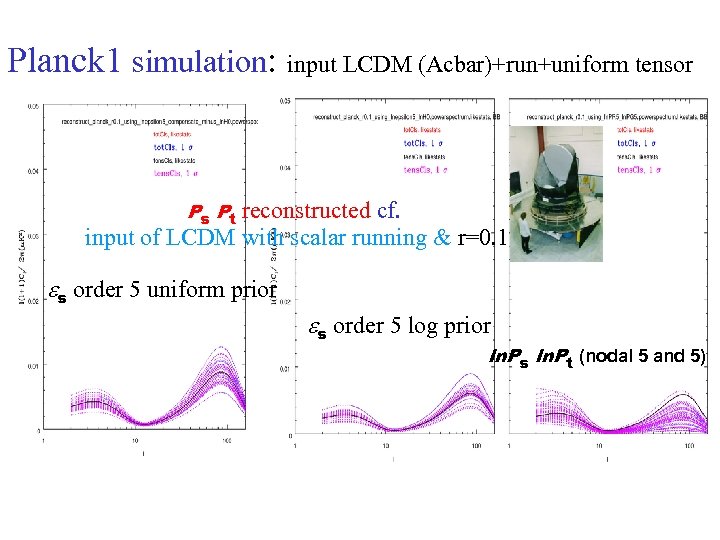
Planck 1 simulation: input LCDM (Acbar)+run+uniform tensor reconstructed cf. input of LCDM with scalar running & r=0. 1 Ps Pt es order 5 uniform prior es order 5 log prior ln. Ps ln. Pt (nodal 5 and 5)

Inflation then summary the basic 6 parameter model with no GW allowed fits all of the data OK Usual GW limits come from adding r with a fixed GW spectrum and no consistency criterion (7 params). Adding minimal consistency does not make that much difference (7 params) r (<. 28 95%) limit comes from relating high k region of 8 to low k region of GW CL Uniform priors in (k) ~ r(k): with current data, the scalar power downturns ( (k) goes up) at low k if there is freedom in the mode expansion to do this. Adds GW to compensate, breaks old r limit. T/S (k) can cross unity. But log prior in drives to low r. a B-pol could break this prior dependence, maybe Planck+Spider. Complexity of trajectories arises in many-moduli string models. Roulette example: 4 -cycle complex Kahler moduli in large compact volume Type IIB string theory TINY r ~ 10 -10 if the normalized inflaton y < 1 over ~50 e-folds then r <. 007 Dy ~10 for power law & PNGB inflaton potentials Prior probabilities on the inflation trajectories are crucial and cannot be decided at this time. Philosophy: be as wide open and least prejudiced as possible Even with low energy inflation, the prospects are good with Spider and even Planck to either detect the GW-induced B-mode of polarization or set a powerful upper limit against nearly uniform acceleration. Both have strong Cdn roles. CMBpol

End
8c74d8950d44e238bf5398ad5d8fb0ac.ppt