f19f25833098875751ede0966bfeabe4.ppt
- Количество слайдов: 34

Development of RF Undulator. Based Insertion Devices for Storage Rings and Free Electron lasers Sami Tantawi, Jeff Neilson, Robert Hettel, Gordon Bowden

Outline • • Background Motivation Approach Work Plan

Undulators • Transverse acceleration of relativistic electron beam produces synchrotron radiation • Usually constructed from static periodic magnets • Main undulator parameters are the period and K – K typically 2 to 3 for static undulators – Typical λu for existing static undulators few cm

RF Undulator Background • Only one referenced construction of undulator Shintake* (1983) • All practical designs to date produce too low of K value to be of much interest • RF limitations – Excessive field level/loss on metallic surfaces – Power levels exceeding available sources *T. Shintake, K. Huke, J. Tanaka, I. Sato and I. Kumabe, ”Development of Microwave Undulator”, Japanese Journal of Applied Physics, May 1983

Why RF Undulator? • Many desirable features – Fast dynamic control of • Polarization • Wavelength • K – Large aperture (cm vs mm for static undulator) – No issue with permanent magnet damage by radiation – Economic considerations – Potential use as LCLS “After Burner” – Dynamic undulator for storage ring

Available Resource - NLCTA • 3 x RF stations – 2 x pulse compressors (240 ns - 300 MW max), driven each by 2 x 50 MW X-band klystrons – 1 x pulse compressors (400 ns – 300 MW /200 ns – 500 MW variable), driven by 2 x 50 MW X-band klystrons. • 1 x Injector: 65 Me. V, ~0. 3 n. C / bunch * * * In the accelerator housing: – 2 x 2. 5 m slots for structures Shielding Enclosure: suitable up to 1 Ge. V For operation: – Can run 24/7 using automated controls (Gain = 3. 1) 3/17/2018 Page 6
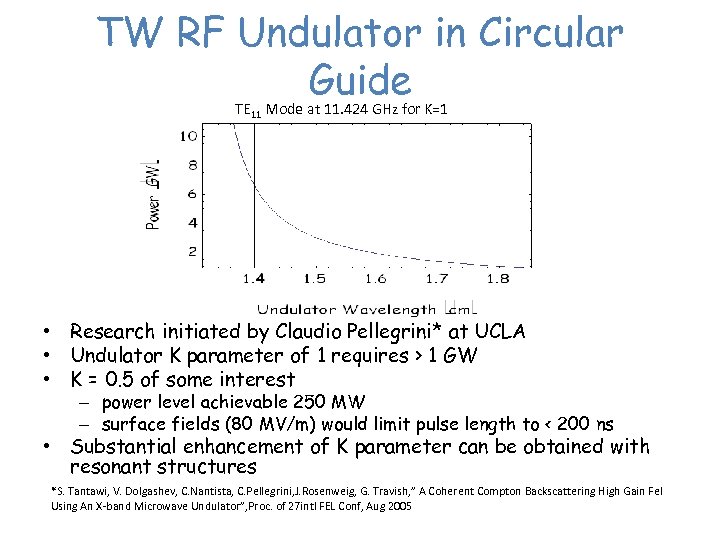
TW RF Undulator in Circular Guide TE 11 Mode at 11. 424 GHz for K=1 • Research initiated by Claudio Pellegrini* at UCLA • Undulator K parameter of 1 requires > 1 GW • K = 0. 5 of some interest – power level achievable 250 MW – surface fields (80 MV/m) would limit pulse length to < 200 ns • Substantial enhancement of K parameter can be obtained with resonant structures *S. Tantawi, V. Dolgashev, C. Nantista, C. Pellegrini, J. Rosenweig, G. Travish, ” A Coherent Compton Backscattering High Gain Fel Using An X-band Microwave Undulator”, Proc. of 27 intl FEL Conf, Aug 2005

Circular waveguide mode TE 11 • Fundamental mode, easily excitable • Has very strong RF field on the axis where the electron bunch travels • Not the least lossy mode Electric field over waveguide cross-section
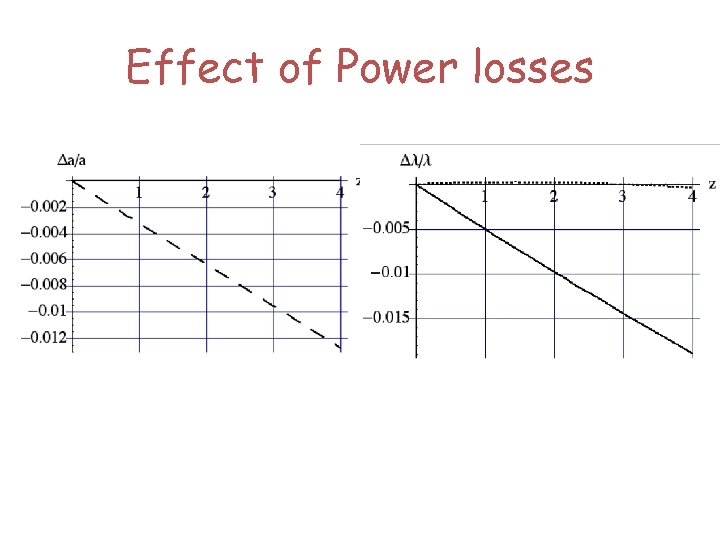
Effect of Power losses
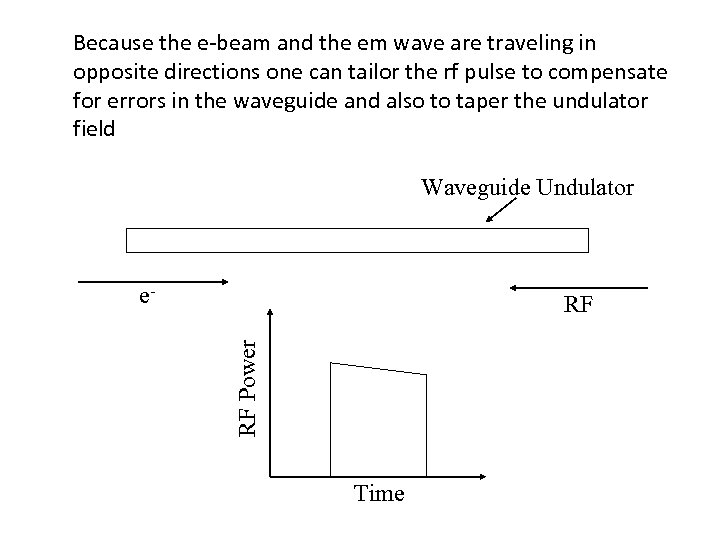
Because the e-beam and the em wave are traveling in opposite directions one can tailor the rf pulse to compensate for errors in the waveguide and also to taper the undulator field Waveguide Undulator e. RF Power RF Time
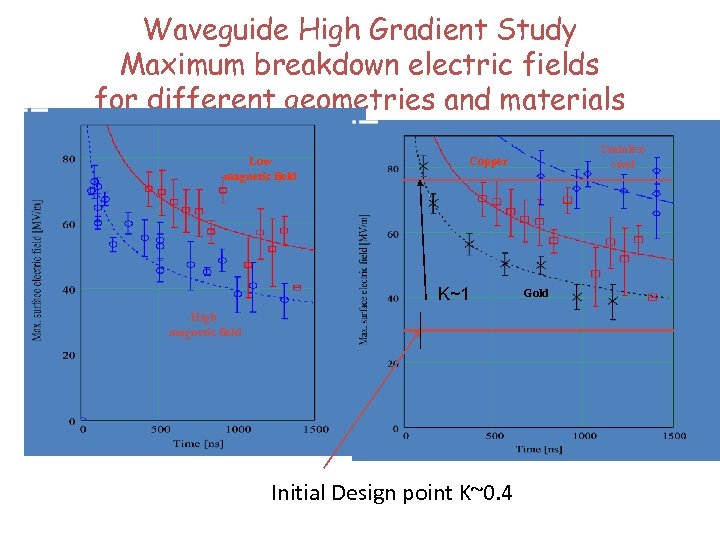
Waveguide High Gradient Study Maximum breakdown electric fields for different geometries and materials Low magnetic field Stainless steel Copper K~1 High magnetic field Initial Design point K~0. 4 Gold

Waveguide Types • Rectangular (Square) – Supports TE and TM modes – High Attenuation – Hard to build • Circular – Supports TE and TM modes – Lower Attenuation – easier to build (I think) but hard to taper • Open Rectangular – Supports TM modes – High Attenuation – Easier to build and taper • Traditional ridge waveguides etc. , will not work because of surface peak fields
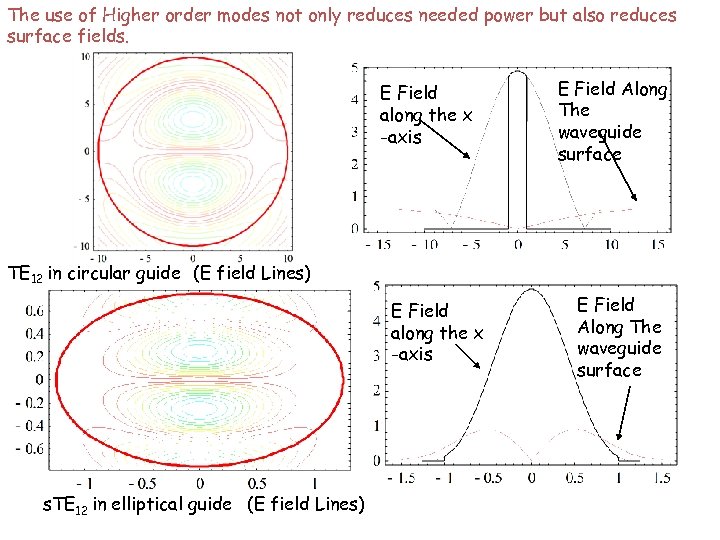
The use of Higher order modes not only reduces needed power but also reduces surface fields. E Field along the x -axis E Field Along The waveguide surface TE 12 in circular guide (E field Lines) E Field along the x -axis s. TE 12 in elliptical guide (E field Lines) E Field Along The waveguide surface
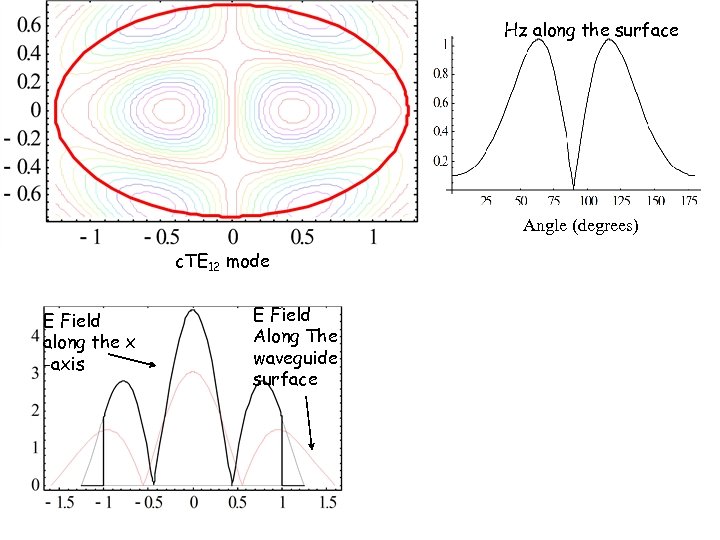
Hz along the surface Angle (degrees) c. TE 12 mode E Field along the x -axis E Field Along The waveguide surface
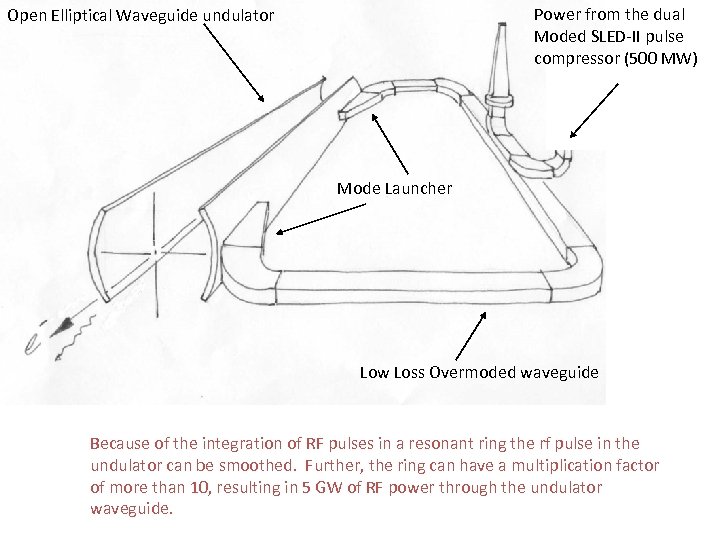
Power from the dual Moded SLED-II pulse compressor (500 MW) Open Elliptical Waveguide undulator Mode Launcher Low Loss Overmoded waveguide Because of the integration of RF pulses in a resonant ring the rf pulse in the undulator can be smoothed. Further, the ring can have a multiplication factor of more than 10, resulting in 5 GW of RF power through the undulator waveguide.
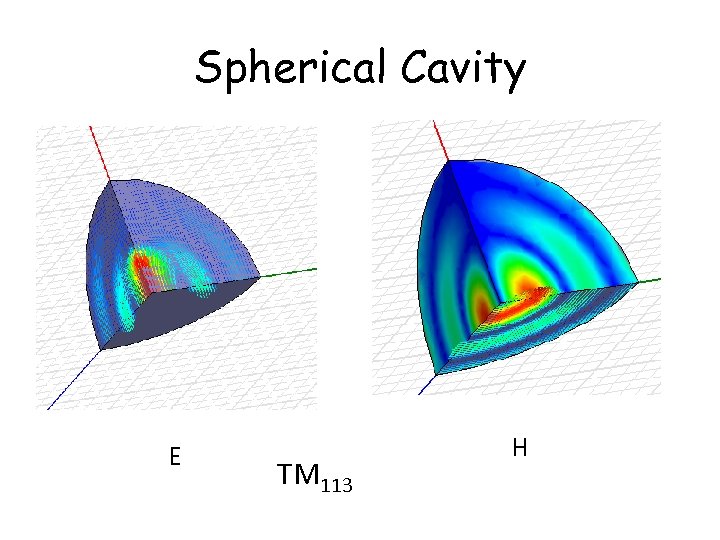
Spherical Cavity E TM 113 H

Cavity Parameters for an Equivalent of 1 T Peak Field at 11. 424 GHz • TE 011 – Diamter : 1. 477” (3. 753 cm) – Power: 2. 67 MW – Maximum H on Surface: 0. 26 MA/m (0. 320 T) – Maximum E on surface: 0 MV/m
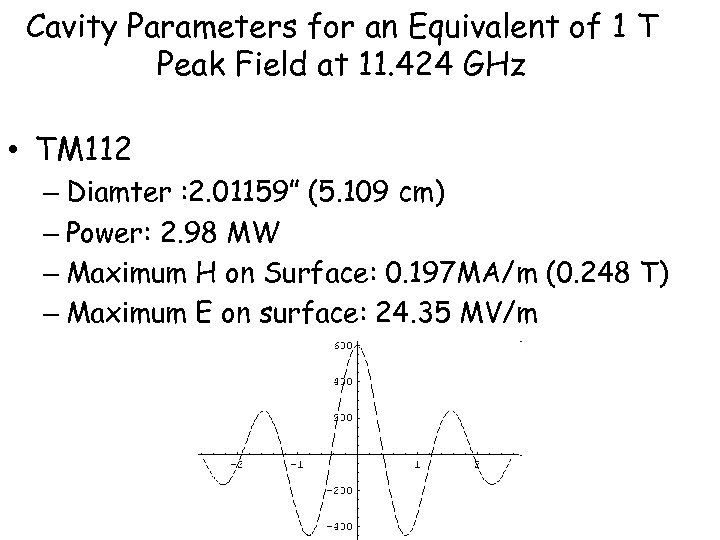
Cavity Parameters for an Equivalent of 1 T Peak Field at 11. 424 GHz • TM 112 – Diamter : 2. 01159” (5. 109 cm) – Power: 2. 98 MW – Maximum H on Surface: 0. 197 MA/m (0. 248 T) – Maximum E on surface: 24. 35 MV/m

The Perl String Undulator • Even with optimized diamter and operating frequency, For a waveguide resonators, the end is a problem. Its losses dominates • Also We need to reduce the average power for a near CW undulator operation. (However, it could be done as superconducting device) • Spherical cavities offer about 35% increase in Q factor over circular cylindrical ones. • Also highly overmoded spherical cavities can have a very low surface fields in comparison with the center field.
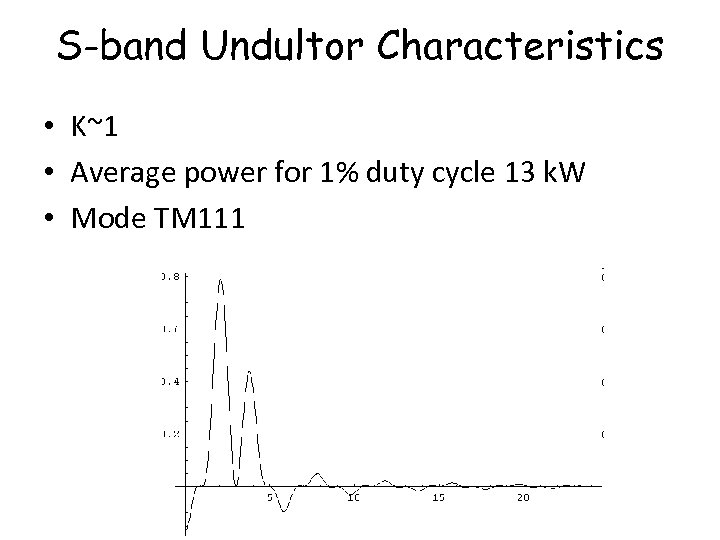
S-band Undultor Characteristics • K~1 • Average power for 1% duty cycle 13 k. W • Mode TM 111

Resonant Waveguide Undulator Cutoff taper Lu=1 -2 m • Instead of increasing the field by operating close to the cutoff frequency of the waveguide undulator one creates a resonant Line • Tuning the radiation wavelength is done through tuning K between 0. 5 to 1 for example: Undulator frequency= 2. 856 GHz Mode: TE 11 Waveguide Radius=3. 22 cm Radiation spectrum from 705 e. V -940 e. V (K~ 0. 5 -1) Power/feed @ K=11. 1 MW (two feeds for two polarizations) The circulating power within the undulator ~569 MW • With the use of nonstandard frequency (~1. 905 GHz) one can reduce the power/feed to about 5 MW. This is done by using TE 12 mode and choosing the diameter of the waveguide such that the line losses is much smaller than the end losses
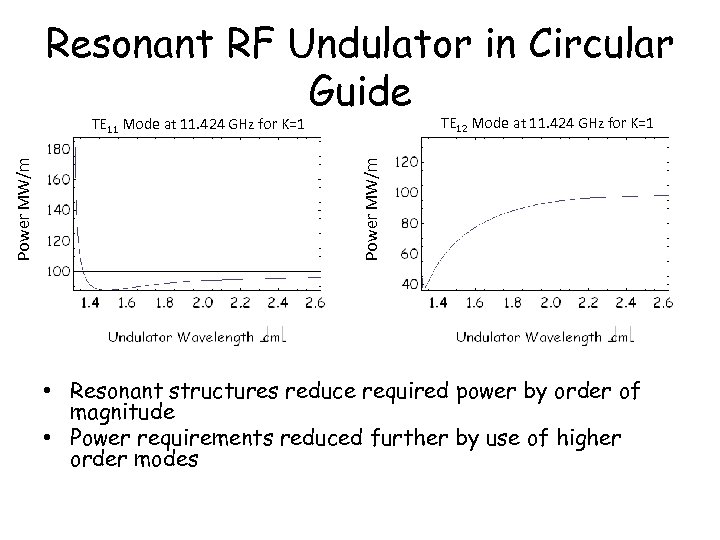
Resonant RF Undulator in Circular Guide TE 12 Mode at 11. 424 GHz for K=1 Power MW/m TE 11 Mode at 11. 424 GHz for K=1 • Resonant structures reduce required power by order of magnitude • Power requirements reduced further by use of higher order modes
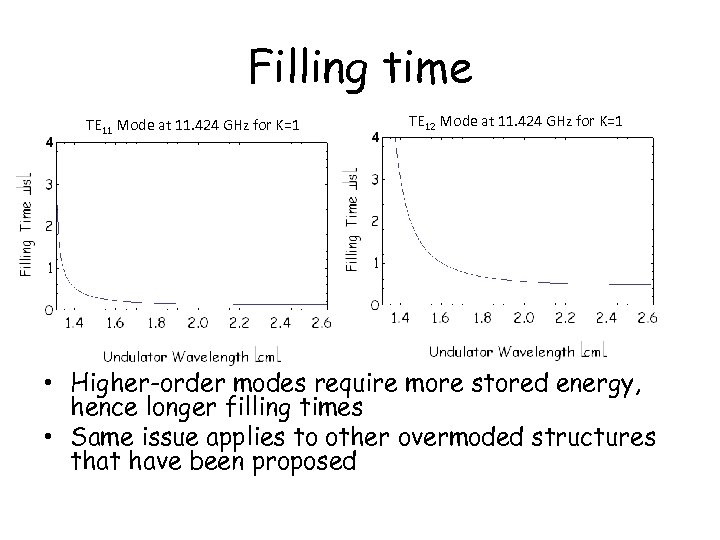
Filling time TE 11 Mode at 11. 424 GHz for K=1 TE 12 Mode at 11. 424 GHz for K=1 • Higher-order modes require more stored energy, hence longer filling times • Same issue applies to other overmoded structures that have been proposed
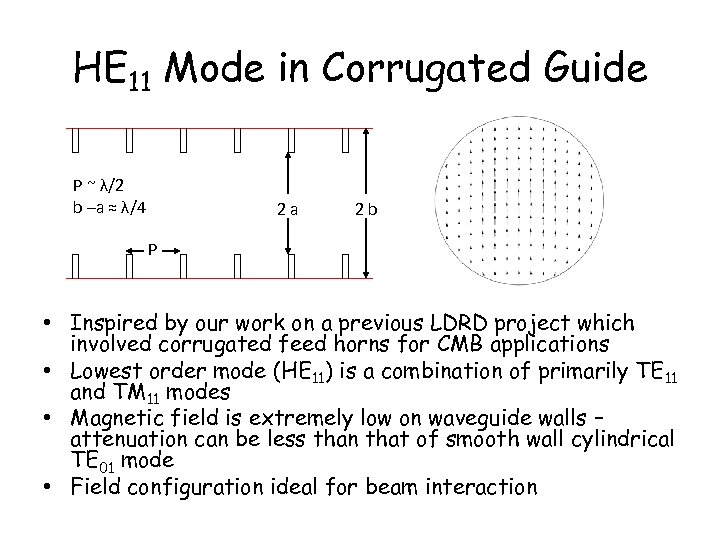
HE 11 Mode in Corrugated Guide P ~ λ/2 b –a ≈ λ/4 2 a 2 b P • Inspired by our work on a previous LDRD project which involved corrugated feed horns for CMB applications • Lowest order mode (HE 11) is a combination of primarily TE 11 and TM 11 modes • Magnetic field is extremely low on waveguide walls – attenuation can be less than that of smooth wall cylindrical TE 01 mode • Field configuration ideal for beam interaction
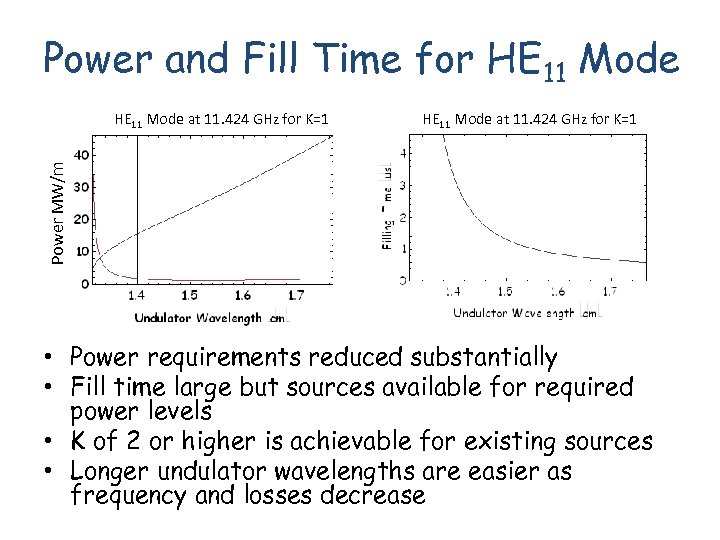
Power and Fill Time for HE 11 Mode at 11. 424 GHz for K=1 Power MW/m HE 11 Mode at 11. 424 GHz for K=1 • Power requirements reduced substantially • Fill time large but sources available for required power levels • K of 2 or higher is achievable for existing sources • Longer undulator wavelengths are easier as frequency and losses decrease
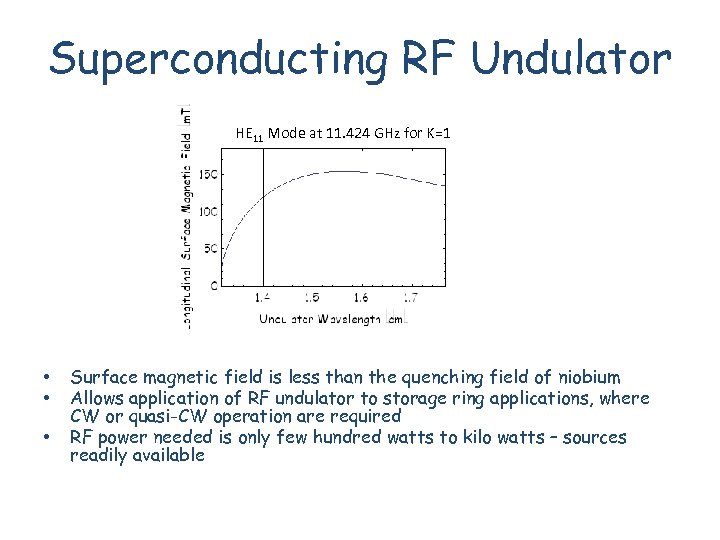
Superconducting RF Undulator HE 11 Mode at 11. 424 GHz for K=1 • • • Surface magnetic field is less than the quenching field of niobium Allows application of RF undulator to storage ring applications, where CW or quasi-CW operation are required RF power needed is only few hundred watts to kilo watts – sources readily available
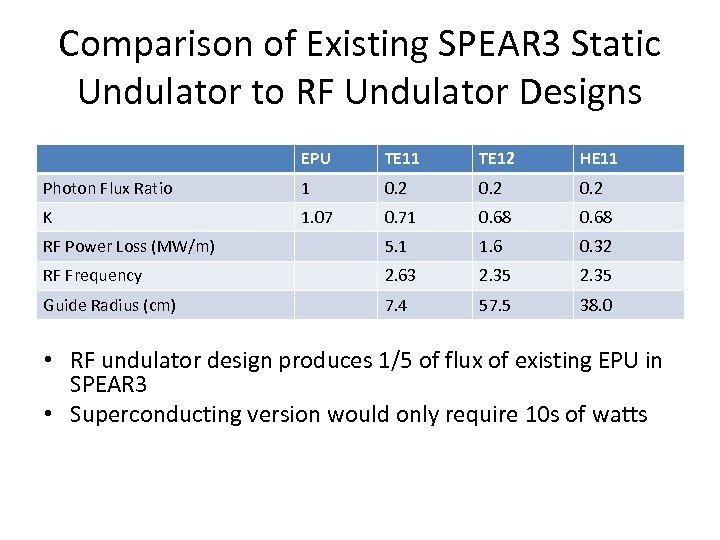
Comparison of Existing SPEAR 3 Static Undulator to RF Undulator Designs EPU TE 11 TE 12 HE 11 Photon Flux Ratio 1 0. 2 K 1. 07 0. 71 0. 68 RF Power Loss (MW/m) 5. 1 1. 6 0. 32 RF Frequency 2. 63 2. 35 Guide Radius (cm) 7. 4 57. 5 38. 0 • RF undulator design produces 1/5 of flux of existing EPU in SPEAR 3 • Superconducting version would only require 10 s of watts
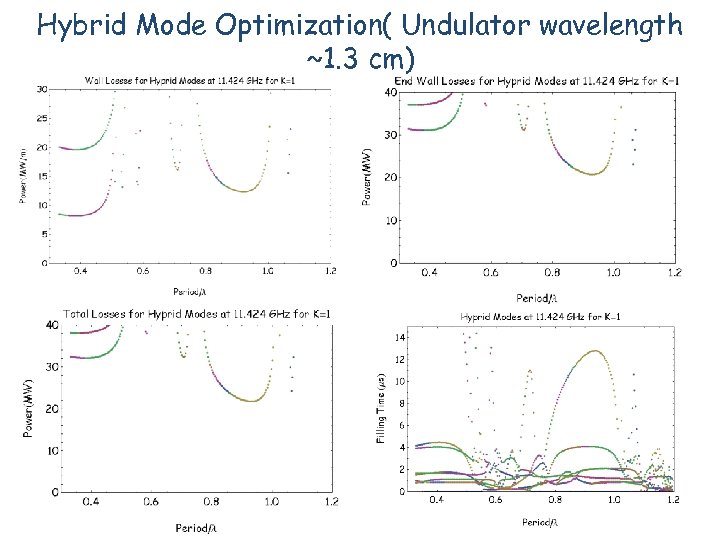
Hybrid Mode Optimization( Undulator wavelength ~1. 3 cm)
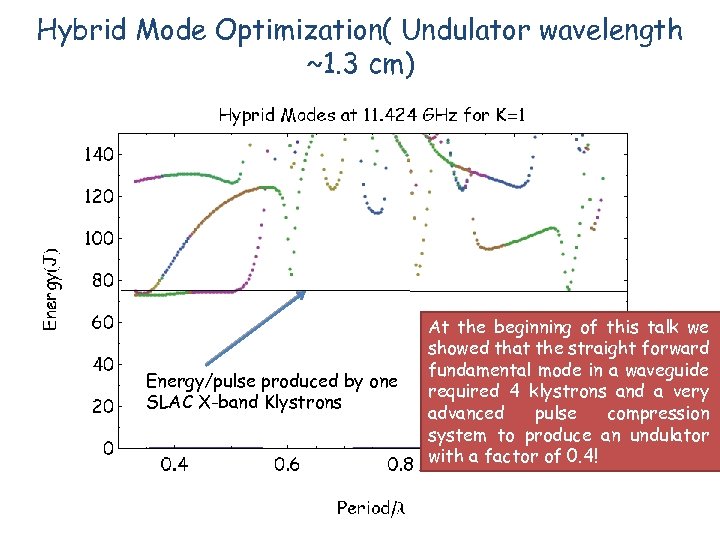
Hybrid Mode Optimization( Undulator wavelength ~1. 3 cm) Energy/pulse produced by one SLAC X-band Klystrons At the beginning of this talk we showed that the straight forward fundamental mode in a waveguide required 4 klystrons and a very advanced pulse compression system to produce an undulator with a factor of 0. 4!
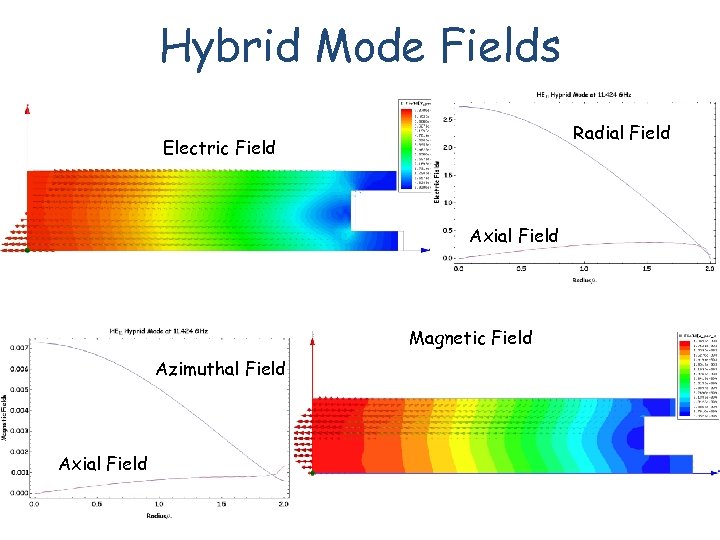
Hybrid Mode Fields Radial Field Electric Field Axial Field Magnetic Field Azimuthal Field Axial Field
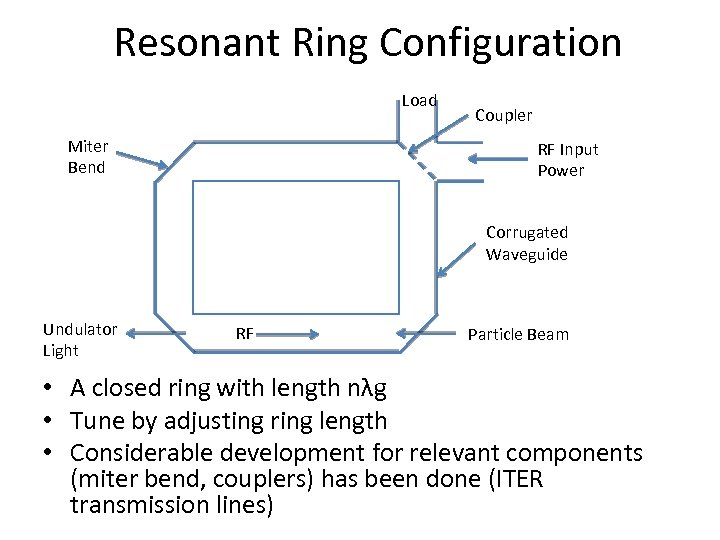
Resonant Ring Configuration Load Miter Bend Coupler RF Input Power Corrugated Waveguide Undulator Light RF Particle Beam • A closed ring with length nλg • Tune by adjusting ring length • Considerable development for relevant components (miter bend, couplers) has been done (ITER transmission lines)

Future Work • Prototype design – Refine corrugated waveguide parameters for optimal performance – Beam impedance calculations – Resonant ring / resonator design • RF feed • Particle beam port • Low power testing of critical components • Construction and test of undulator – – HOM damping design as necessary for storage ring applications Mechanical design Construct and test at NLCTA If successful apply for more funds for testing either with LCLS or SSRL

Test at NLCTA • Injector Parameters – 50 Me. V beam energy – 200 A peak current – Normalized emittance 2 mm mrad? ? – Relative energy spread 5 X 10 -4 • RF system – 11. 424 GHz – Peak power 600 MW at 400 ns or 150 MW 1. 5 us • Accelerator – Up to 120 Me. V

Conclusions • Use of HE 11 mode provides key to first practical application of RF undulators • Successful development will enable design of undulators with capabilities not possible with current static undulators • Could lead to a new class of FEL and storage ring undulators
f19f25833098875751ede0966bfeabe4.ppt