73bed2e1d93f57465dc537405ca62a89.ppt
- Количество слайдов: 32

Deutsche Bank Common Option Strategies Alan L. Tucker, Ph. D. 631 -331 -8024 (tel) 631 -331 -8044 (fax) tucker@mtaglobal. com Copyright © 1997 -2001 Marshall, Tucker & Associates, LLC All rights reserved 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 1

ALAN L. TUCKER, Ph. D. Alan L. Tucker is Associate Professor of Finance at the Lubin School of Business, Pace University, New York, NY and an Adjunct Professor at the Stern School of Business of New York University, where he teaches graduate courses in derivative instruments. Dr. Tucker is also a principal of Marshall, Tucker & Associates, LLC, a financial engineering and derivatives consulting firm with offices in New York, Chicago, Boston, San Francisco and Philadelphia. Dr. Tucker was the founding editor of the Journal of Financial Engineering, published by the International Association of Financial Engineers (IAFE). He presently serves on the editorial board of Journal of Derivatives and the Global Finance Journal and is a former associate editor of the Journal of Economics and Business. He is a former director of the Southern Finance Association and a former program co-director of the 1996 and 1997 Conferences on Computational Intelligence in Financial Engineering, co-sponsored by the IAFE and the Neural Networks Council of the IEEE. Dr. Tucker is the author of three books on financial products and markets: Financial Futures, Options & Swaps, International Financial Markets, and Contemporary Portfolio Theory and Risk Management (all published by West Publishing, a unit of International Thompson). He has also published more than fifty articles in academic journals and practitioner-oriented periodicals including the Journal of Finance, the Journal of Financial and Quantitative Analysis, the Review of Economics and Statistics, the Journal of Banking and Finance, and many others. Dr. Tucker has contributed to the development of theory of derivative products including futures, options and swaps, and to theory of international capital markets and trade. He has also contributed to theory of technology adoption over the life-cycle. The Social Sciences Citation Index shows that his research has been cited in refereed journals on over one hundred occasions. As a consultant, Dr. Tucker has worked for The United States Treasury Department, the United States Justice Department, Morgan Stanley Dean Witter, Union Bank of Switzerland, LG Securities (Korea), and Chase Manhattan Bank. Dr. Tucker holds the B. A. in economics from La. Salle University (1982), and the MBA (1984) and Ph. D. (1986) in finance from Florida State University. He was born in Philadelphia in 1960, is married (Wendy) and has three children (Emily, 1993, Michael and Matthew, both 1995). 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 2

Common Option Strategies Purpose. The purpose of this presentation is to illustrate common option trading strategies. Our focus will be on three types of strategies: (1) Those that capture potential profits arising from how realized/future volatility comports with a trader’s “view” on volatility. (2) Strategies that capture arbitrage profits arising from differences in the values of embedded options and their actual or synthetic counterparts. (3) Collar trades and related trades designed for the particular needs of certain high net worth retail clients. 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 3

Common Option Strategies • Keep in mind the following throughout our discussion: – Strategies (1) and (2) are appropriate for institutional traders whereas (3) is appropriate for retail clients. – With (1), a trader (e. g. , a “volatility directional hedge fund” or the “prop desk”) is taking a position in vol and thus profitability depends critically on whether or not his “view” proves correct. Limits on an options dealer, e. g. , a limit on the vega of a dealer’s book, prevent excessive losses and therefore limit gains from these types of strategies. – The arbitrage strategies (2) are also generally the purview of hedge funds and other “buy side” entities. 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 4

Common Option Strategies Example 1. Assume that for a particular stock, a trader believes that the stock’s implied volatility term structure is too low, as illustrated below. (Potential reasons motivating this and other views will be discussed shortly. Note that the example could just as readily be imparted in terms of forward implied volatility term structures. ) How can a trader “monetize” the move from implied to predicted volatility? Volatility Predicted Vol Implied Vol Option Maturity 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 5

Common Option Strategies In this example, the trader wants to be “long vol” to profit from a rise in option premium occasioned by an upward shift in the implied volatility term structure toward that predicted. To be “long vol” while simultaneously immunizing against changes in the stock price, the trader wants to assume a position that is delta and gamma neutral but exhibits a positive vega. For instance, suppose that the trader wants a delta and a gamma of 0 and a vega of say +210, 000. In order to change N greeks/risk metrics, one has to trade at least N+1 assets. Let there be two actively traded options on the stock (with maturity equal to or extending beyond the relevant segment of the implied volatility term structure) having the following greeks: 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 6
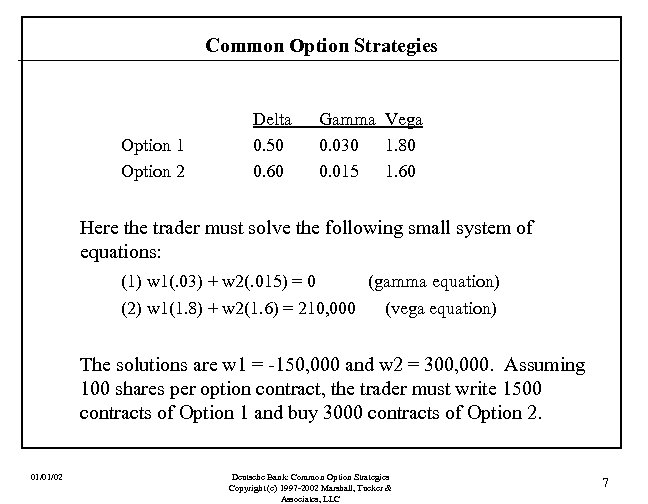
Common Option Strategies Option 1 Option 2 Delta 0. 50 0. 60 Gamma Vega 0. 030 1. 80 0. 015 1. 60 Here the trader must solve the following small system of equations: (1) w 1(. 03) + w 2(. 015) = 0 (gamma equation) (2) w 1(1. 8) + w 2(1. 6) = 210, 000 (vega equation) The solutions are w 1 = -150, 000 and w 2 = 300, 000. Assuming 100 shares per option contract, the trader must write 1500 contracts of Option 1 and buy 3000 contracts of Option 2. 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 7

Common Option Strategies At this point, the trader has a delta of: (-150, 000)(. 50) + 300, 000(. 60) = 105, 000. Therefore, the trader must sell off from inventory or short 105, 000 shares in order to delta hedge. The new book vega of 210, 000 suggests that the trader will have an instantaneous profit of about $2, 100 should the implied volatility term structure shift up (in a parallel fashion) by 0. 01. Why “instantaneous”? (Dynamic trading to hit bogies. ) Why “about $2, 100”? (Option prices are non-linear in vol. ) How many asset were traded? (N+1 rule. ) Is the new vega within limits? (Risk tolerance. ) 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 8

Common Option Strategies What would happen if the implied volatility term structure was perceived as too high? Then the trader would want to be “short vol”. That is, the trader would want to be delta and gamma neutral and simultaneously carry a targeted vega that was negative. In general, is it more dangerous to be long vol or short vol? The answer is short vol because volatility can go up without bound whereas it can only go down to zero. Like stock prices, volatility is reasonably described by a log-normal distribution. 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 9

Common Option Strategies For equities in general, which strategy has made money recently, being long vol or being short vol? The answer is short vol, at least since the beginning of the 2001 calendar year. Option time values were “taken in” during 2001 arguably because there has been a “volatility supply glut” or “volatility overhang”. If one thinks of volatility as a commodity like wheat, then it is feasible that the “price of equity volatility” (option time values) can fall if there is a volatility overhang. Excessive volatility supply can lower option time value and therefore implied volatility, thus making a short vol strategy profitable. This recent vol overhang in the equity market (a “vol crush”) appears to be driven by the growth in the convertible bond issuance marketplace. For most of 2001, convertibles made up about 55% of the total equity issuance marketplace. This compares with a figure of just 17% in 1999. Convertibles of course have embedded equity options, and thus the increased supply of vol. 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 10

Common Option Strategies The reason for this increase in convertibles appears to be two-fold: (1) certain perceived tax and accounting advantages to convertibles (e. g. , an issuer avoids having to report more fully-diluted EPS under a convertible than under a straight-equity follow-on issue). And (2), a recent propensity for investmentgrade firms to issue convertibles, whereas the convertible marketplace has traditionally been composed of non-investment grade issuers (78% in 1999 but only about 37% in 2001) seeking to lower their coupon rates. This may be due to these firms no longer viewing their equity as “cheap currency”. On the other hand, being long vol tended to be the winning strategy throughout most of the second half of the 1990 s as the Asian crisis, LTCM crisis, and other crises tended to inflate volatility. For instance, the implied vol of the 6 -month S&P 500 rose from about 12% in January of 1995 to about 22% in December 1999, and hit a high of about 35% in the first quarter of 1999. Being long vol has also been profitable since the events of 11 September 2001. 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 11

Common Option Strategies The preceding discussion of convertibles and volatility overhang suggests another recently popular trading strategy undertaken by so-called “relative value volatility funds”. Here the funds short options written on companies that have issued convertibles (either by purchasing the individual convertible bonds and financing the purchases via the repo market, or writing options on a basket of the common stocks of the issuing companies), and simultaneously long options written on a basket of non-convertible common stocks. The idea of course is to wager on a relative volatility compression between the two types of companies - convertible bond issuing and non-issuing. 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 12

Common Option Strategies Example 2. Suppose that a trader feels that a stock’s implied volatility, at a particular point or segment on its implied vol term structure, is temporarily high and will revert toward the general level of the rest of the term structure. How can the trader capture value here? Here the trader will want to be short vol with respect to this particular point/segment on the term structure, but will want to be vega neutral for the other segments of the term structure. The easiest solution is to trade a forward-starting option whose value would be principally driven by the relevant forward implied vol. 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 13
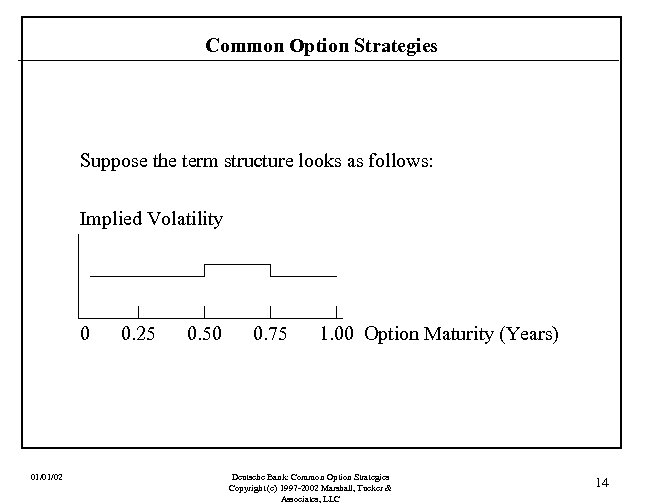
Common Option Strategies Suppose the term structure looks as follows: Implied Volatility 0 01/01/02 0. 25 0. 50 0. 75 1. 00 Option Maturity (Years) Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 14

Common Option Strategies Writing the 9 -month option and buying the counterpart 6 -month option would have the effect of carving out a short position in a 3 -month option whose maturity begins in 6 months. An OTC trade would simply be a short position in a straight forwardstarting option. Either way, the trader’s vega exposure is isolated to the relevant segment of the implied volatility term structure. So the trader would have a negative vega with respect to the 3 -month forward vol six months hence. Note, however, that while the trader can delta hedge in the usual fashion there will remain some gamma risk exposure from this strategy. 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 15
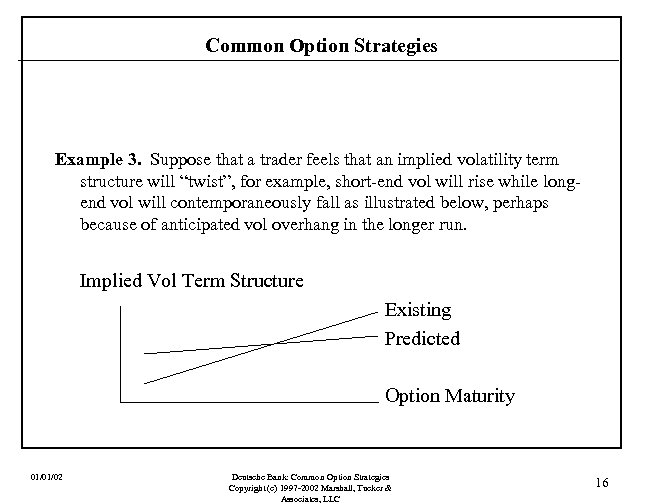
Common Option Strategies Example 3. Suppose that a trader feels that an implied volatility term structure will “twist”, for example, short-end vol will rise while longend vol will contemporaneously fall as illustrated below, perhaps because of anticipated vol overhang in the longer run. Implied Vol Term Structure Existing Predicted Option Maturity 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 16
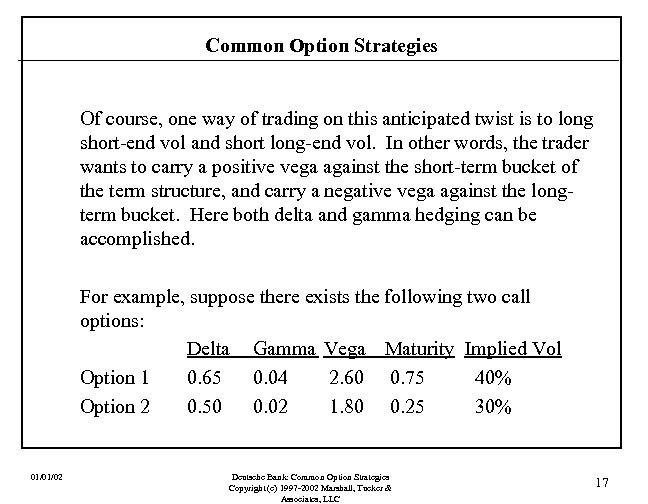
Common Option Strategies Of course, one way of trading on this anticipated twist is to long short-end vol and short long-end vol. In other words, the trader wants to carry a positive vega against the short-term bucket of the term structure, and carry a negative vega against the longterm bucket. Here both delta and gamma hedging can be accomplished. For example, suppose there exists the following two call options: Delta Gamma Vega Maturity Implied Vol Option 1 0. 65 0. 04 2. 60 0. 75 40% Option 2 0. 50 0. 02 1. 80 0. 25 30% 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 17

Common Option Strategies If the trader wants an exposure to the long vol of about -25, 000 vega and an exposure to the short vol of about +30, 000 vega, then he could write 100 contracts of Option 1 and buy 200 contracts of Option 2. The short vol vega would be (-100)(2. 6) = -26, 000 and the long vol vega would be (200)(1. 8) = 32, 000. The gamma position would then be zero: (-100)(. 04) + (200)(100)(. 02) = 0. The delta position would be 3, 500: (-100)(. 65) + (200)(100)(. 50) = 3, 500. The trader could short 3, 500 shares of the stock to delta hedge. Thus the trader would have zero delta and gamma and nearly the vegas desired. Obviously, the term structure would have to twist in the direction predicted, and do so before the expiration of the shortermaturity option, to occasion profits. Also, the positions would need to be re-balanced over time. 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 18

Common Option Strategies Example 4. Suppose that a trader computes two types of volatility term structures - an implied vol term structure based on current option market data, and a historic vol term structure based on a GARCH(1, 1) model. (See “Understanding Volatility”. ) The historic term structure is both downward sloping and everywhere below that of the implied term structure. Because a GARCH model accommodates mean reversion in the term structure, this scenario would suggest two things: first, implied vols may be too high in general and, second, volatility will temper as it is rolled-out in time. To capture profits from the latter, a trader would write short-term options, buy them back as they unwind, and repeat this process through time. 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 19

Common Option Strategies Example 5. Suppose that an option dealer convinces his desk manager as well as the middle office that current implied vol is historically high and that implied vol is mean reverting (see J. Stein, J. of Finance, 1989). This dealer would want to write options at prices reflecting the current and high implied vol, but base his hedging strategies on the lower, long-run vol to which the implied vol will presumable revert. For example, suppose the implied vol for a stock option is 70% while the historic average is , say, 40%. The dealer writes one contract, with a delta - based on the 70% vol - of 0. 60. The delta would thus be (100)(. 60) = -60, implying the need to purchase 60 shares to delta hedge. But here the dealer conducts his delta hedging based on the historic vol of 40%, which occasions a delta of, say, just 0. 50. So the dealer only purchases 50 shares of stock. This will lower the financing costs of delta hedging. If the implied vol reverts to the historic average, then the purchase of 50 shares will have proved an adequate hedge, ceteris paribus. 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 20

Common Option Strategies Example 6. Traditional volatility wagers for retail traders included straddles and their variants (straps and strips), butterfly spreads, calendar spreads, and the like. Volatility wagers for more sophisticated buy-side clientele include: -Range Accrual Notes. Here the investor is paid a fixed amount for every day a specified stock or stock index remains within a fixed range. Buyers make profits when vol is low and writers make profits when vol is high. -Range Options. Here the investor has a payoff that is a function of the realized range of the underlying stock value. 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 21

Common Option Strategies Consider the following range option payoff: MAX{0, [(S(0) x k 1)/(R + k 2) - X]}, where R represents the realized range of the underlying asset. Here the call buyer would be short vol, implying that this option has a negative vega. For instance, let S(0) = X = $25, k 1 = 6, and k 2 = 0. At inception, this option would have infinite intrinsic value as R is zero. Thus the option value can only go down as the option unwinds (a positive theta). As the stock price changes and the range, R, grows, eventually the option will be knocked out (a dual-barrier option with a stochastic knockout price). Why? By letting k 2 be positive, the call writer has limited liability. Why? The option’s value (and therefore its greeks) is also influenced by where the current stock price is relative to the already realized range. Why? 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 22

Common Option Strategies Example 7. Now let us turn our attention to pure vol arbitrage. Perhaps one of the earliest examples of vol arbitrage involved callable bonds. During the second half of the 1980’s, interest rate derivative desks discovered that the call option embedded in a callable bond could be replicated by a swaption. As a result, underwriters, working with their interest rate derivatives desks, schooled corporate treasury officers on how to issue a callable bond and then sell-off (economically speaking) the embedded call by writing a swaption. If the embedded call could be purchased cheaply by the corporate issuer, that is, the added coupon was small compared to the straight-bond alternative, then the corporation’s overall funding cost would be lower (than the straightdebt alternative) after selling off the call by writing the swaption. At the end of the day, the embedded call was cheaper if its implied vol was lower than that of the swaption. We have: 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 23

Common Option Strategies Issue callable bond + Write a swaption Issue straight debt (Issue straight bond and buy back a call) (Sell off the embedded call) (Lower coupon than issuing straight debt directly if the implied vol of the swaption is greater than that of the embedded call) Of course, the investment bank could help discover value for the buyside under this same process. If the implied vol of the embedded call is greater than that of the swaption, then the investor could buy the bond (possibly financing the purchase in the repo market) and buy the swaption. To isolate the value more precisely, the buyer could hedge the credit risk of the bond with a credit derivative. 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 24

Common Option Strategies This process is essentially repeated now in the convertible bond arbitrage game. The following attachment demonstrates how an investor can engage in volatility arbitrage related to differences in implied vol between the embedded option in the convertible and an actual or synthetic option on the stock. (See attachment titled “Convertible Bond Arbitrage”. ) 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 25

Common Option Strategies • Example 8. Zero-cost collars and their variants are popular strategies applicable to certain high net-worth retail clients. (Currently there about 60, 000 U. S. citizens whose net worth is $30 million or more. ) The attachments titled “Constructive Sales and Contingent Payment Puts” and accompanying “Proof” provide detail. 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 26
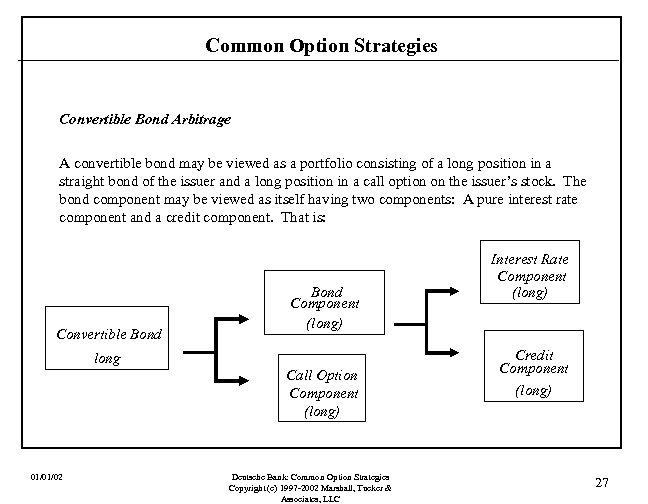
Common Option Strategies Convertible Bond Arbitrage A convertible bond may be viewed as a portfolio consisting of a long position in a straight bond of the issuer and a long position in a call option on the issuer’s stock. The bond component may be viewed as itself having two components: A pure interest rate component and a credit component. That is: Convertible Bond Component (long) long Call Option Component (long) 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC Interest Rate Component (long) Credit Component (long) 27
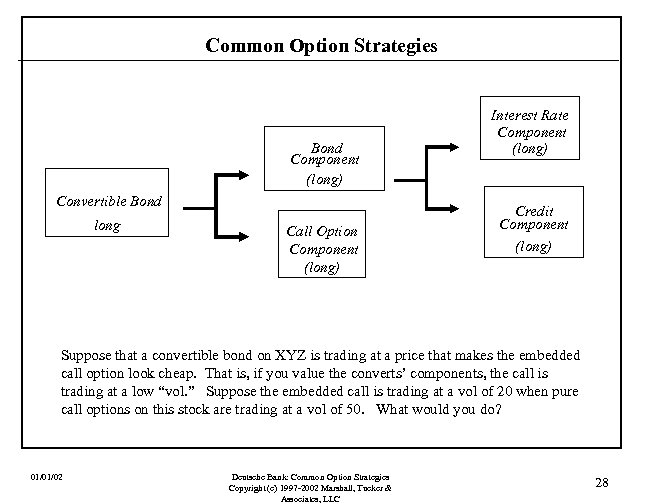
Common Option Strategies Bond Component (long) Convertible Bond long Call Option Component (long) Interest Rate Component (long) Credit Component (long) Suppose that a convertible bond on XYZ is trading at a price that makes the embedded call option look cheap. That is, if you value the converts’ components, the call is trading at a low “vol. ” Suppose the embedded call is trading at a vol of 20 when pure call options on this stock are trading at a vol of 50. What would you do? 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 28
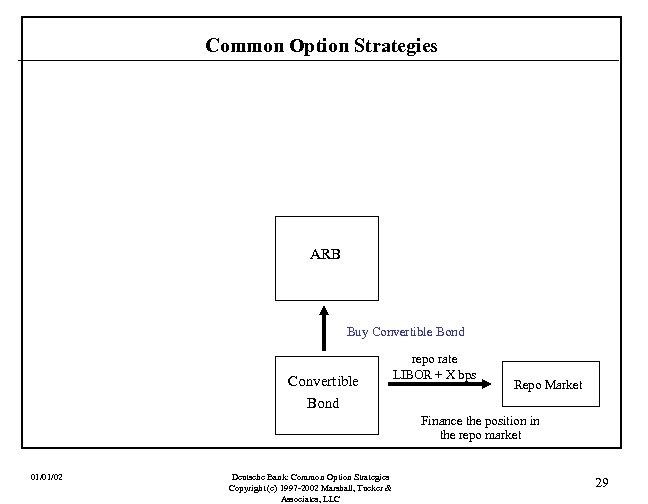
Common Option Strategies ARB Buy Convertible Bond repo rate LIBOR + X bps Repo Market Finance the position in the repo market 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 29
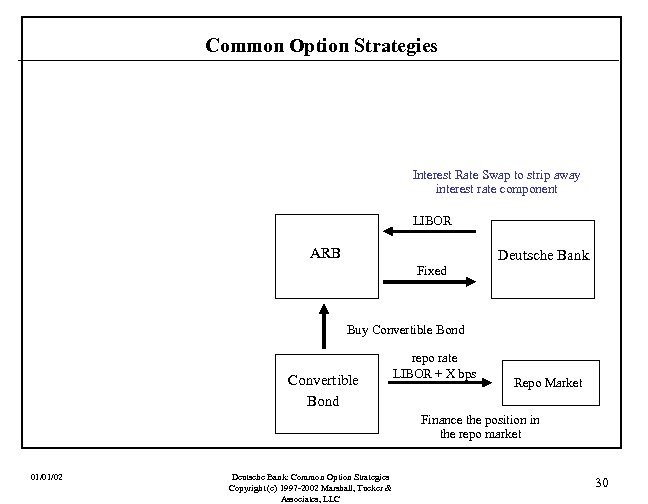
Common Option Strategies Interest Rate Swap to strip away interest rate component LIBOR ARB Deutsche Bank Fixed Buy Convertible Bond repo rate LIBOR + X bps Repo Market Finance the position in the repo market 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 30
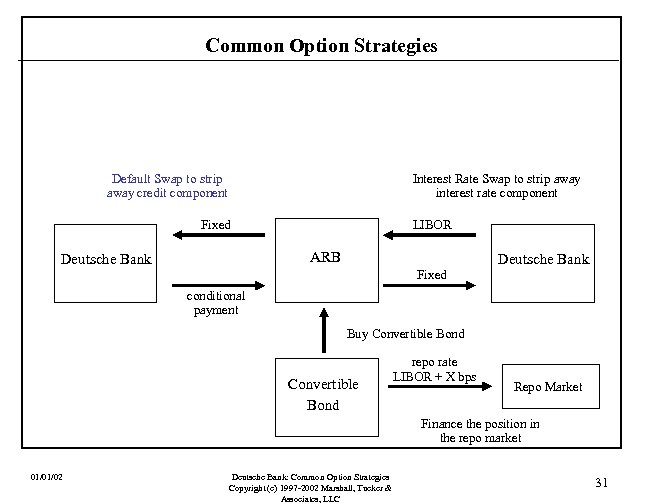
Common Option Strategies Default Swap to strip away credit component Interest Rate Swap to strip away interest rate component Fixed LIBOR ARB Deutsche Bank Fixed conditional payment Buy Convertible Bond repo rate LIBOR + X bps Repo Market Finance the position in the repo market 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 31
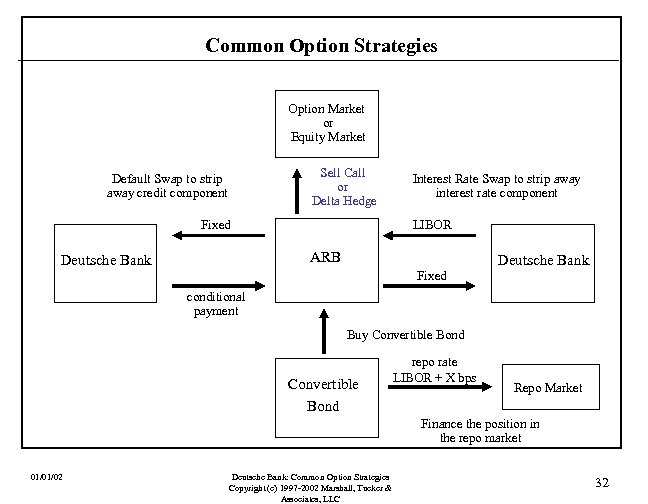
Common Option Strategies Option Market or Equity Market Sell Call or Delta Hedge Default Swap to strip away credit component Fixed Interest Rate Swap to strip away interest rate component LIBOR ARB Deutsche Bank Fixed conditional payment Buy Convertible Bond repo rate LIBOR + X bps Repo Market Finance the position in the repo market 01/01/02 Deutsche Bank: Common Option Strategies Copyright (c) 1997 -2002 Marshall, Tucker & Associates, LLC 32
73bed2e1d93f57465dc537405ca62a89.ppt