Determining the internal structure of extrasolar planets and

Determining the internal structure of extrasolar planets, and the phenomenon of retrograde planetary orbits Rosemary Mardling School of Mathematical Sciences Monash University

Binary stars and apsidal motion double-line eclipsing binary - all parameters known except k 2

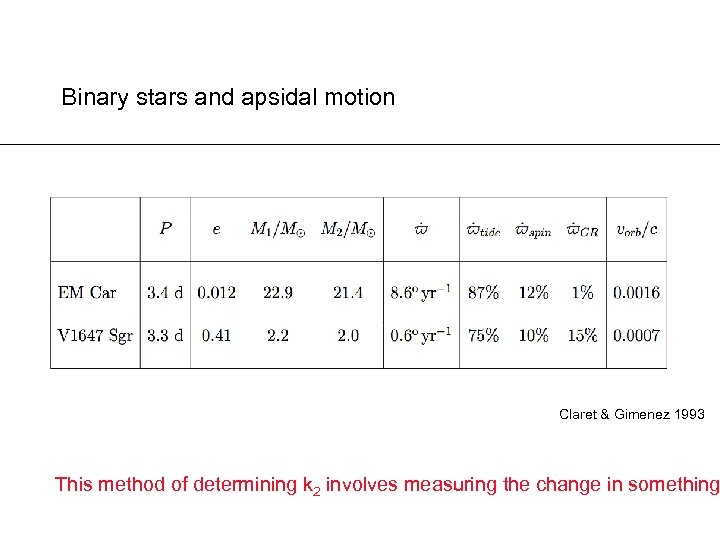Binary stars and apsidal motion Claret & Gimenez 1993 This method of determining k 2 involves measuring the change in something

planets and apsidal motion b k 2 is now called the LOVE NUMBER (= twice apsidal motion constant) Circularization timescale ~ 108 yr; age ~ 5 Gyr b = 181± 46 o __ error MUCH bigger than change per year

Tidal evolution of (isolated) binaries and short-period planets The minimum-energy state of a binary system (or star + planet) is: • circular orbit • rotational frequencies = orbital frequency • spin axes aligned with orbit normal ? ? Definition of short-period planet -- circularization timescale less than the age of the system

Tidal evolution of short-period planets with companions • Many short-period planets have non-zero eccentricities AND anomolously large radii (eg. e = 0. 05, Rp = 1. 4 Jupiter radii) • Bodenheimer, Lin & Mardling (2001) propose that they have undetected companion planets • Mardling (2007): a fixed-point theory for tidal evolution of short-period planets with companions (coplanar) - developed to understand inflated planets • Batygin, Bodenheimer & Laughlin (2009) use this to deduce information about the internal structure of HAT-P-13 b

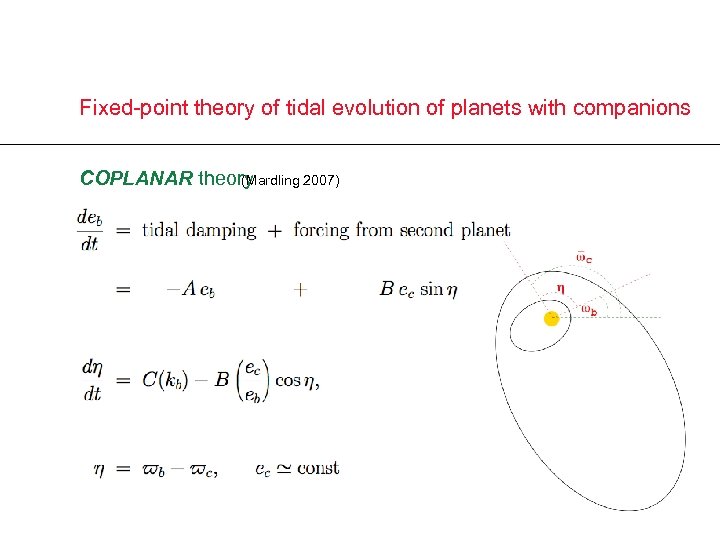Fixed-point theory of tidal evolution of planets with companions COPLANAR theory (Mardling 2007)

Fixed-point theory of tidal evolution of planets with companions COPLANAR theory

Fixed-point theory of tidal evolution of planets with companions

Fixed-point theory of tidal evolution of planets with companions all parameters known except

Fixed-point theory of tidal evolution of planets with companions

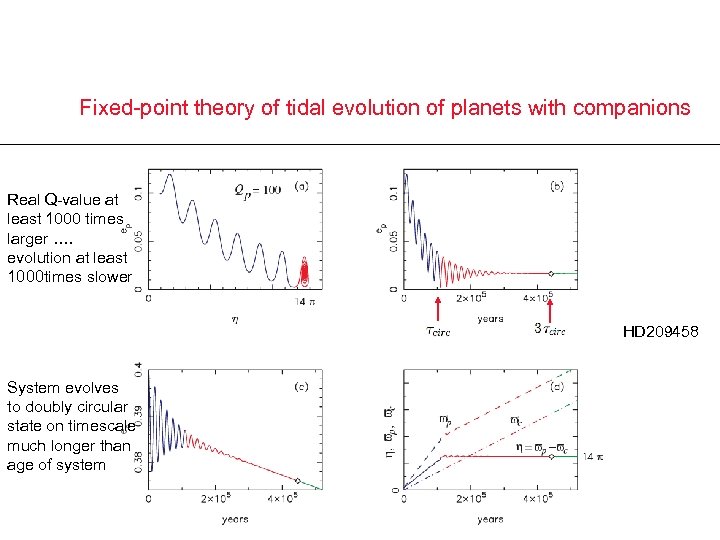Fixed-point theory of tidal evolution of planets with companions Real Q-value at least 1000 times larger …. evolution at least 1000 times slower HD 209458 System evolves to doubly circular state on timescale much longer than age of system

Fixed-point theory of tidal evolution of planets with companions Equilibrium eccentricity substantial if: • • • large (there are interesting exceptions) not too small large HAT-P-13:

The HAT-P-13 system data from Bakos et al 2009 HATNet transit discovery (Cf. A) Keck followup spectroscopy Kepler. Cam followup photometry

The HAT-P-13 system Measured value of (Spitzer will improve data in Dec) Batygin et al: use fixed-point theory to determine hence and This in turn tells us whether or not the planet has a core.

The HAT-P-13 system best fit Given mb, Rb, Teff, find mcore, Ltide from grid of models kb, Qb kb/Ltide, eb(e

However… A system with such a high outer eccentricity is highly unlikely to be COPLANAR! The high eccentricity of planet c may have been produced during a scattering event: Once upon a time there existed a planet d…. .

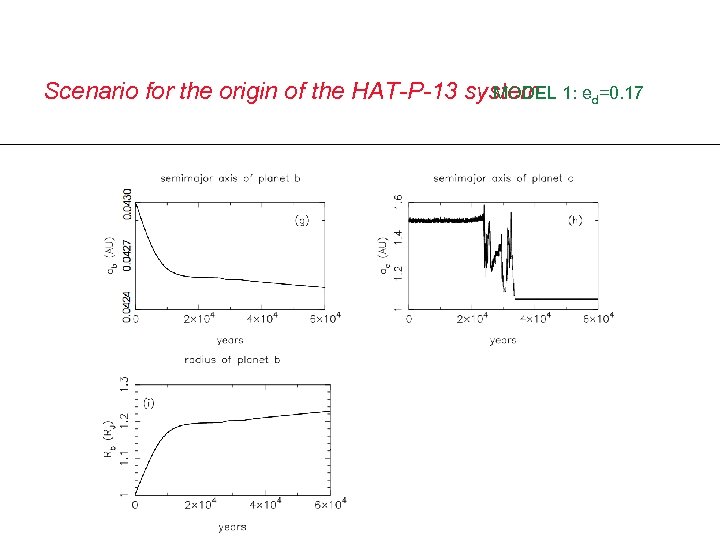
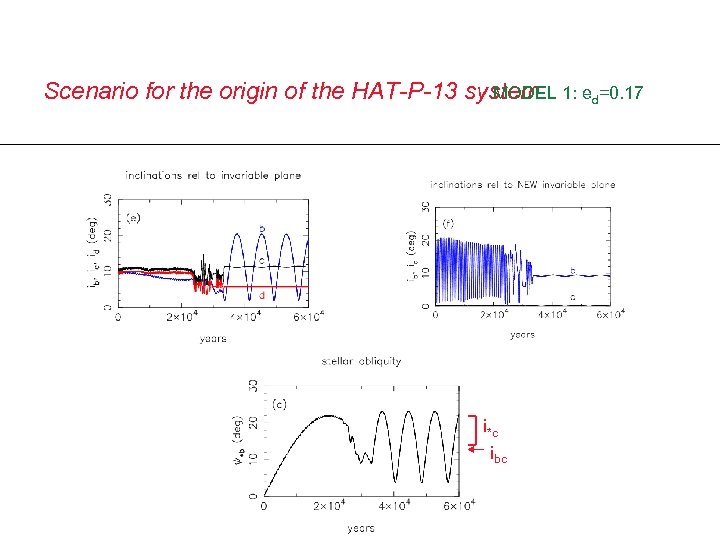
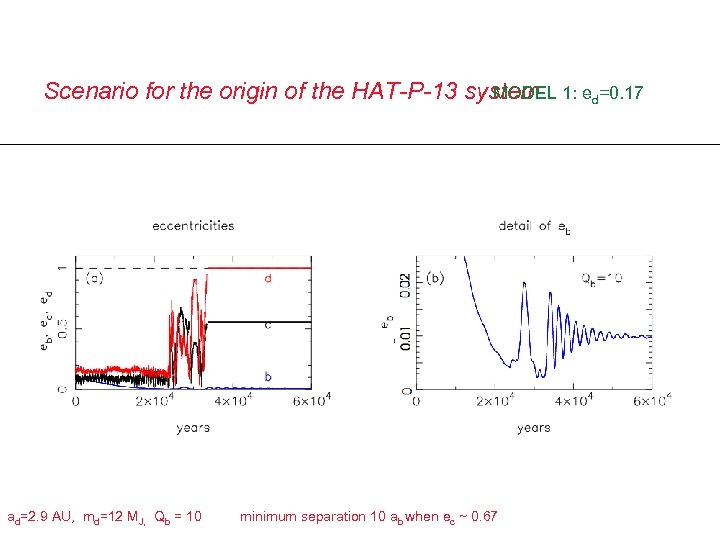Scenario for the origin of the HAT-P-13 system 1: ed=0. 17 MODEL ad=2. 9 AU, md=12 MJ, Qb = 10 minimum separation 10 ab when ec ~ 0. 67

Scenario for the origin of the HAT-P-13 system 1: ed=0. 17 MODEL

Scenario for the origin of the HAT-P-13 system 1: ed=0. 17 MODEL i*c ibc

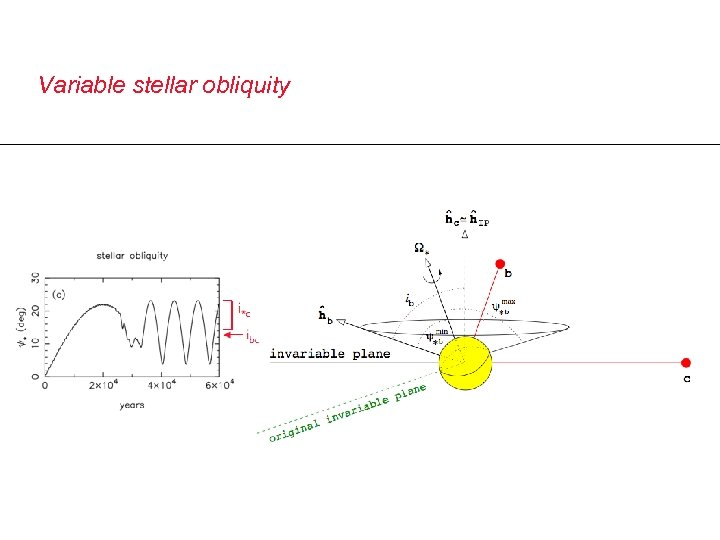Variable stellar obliquity

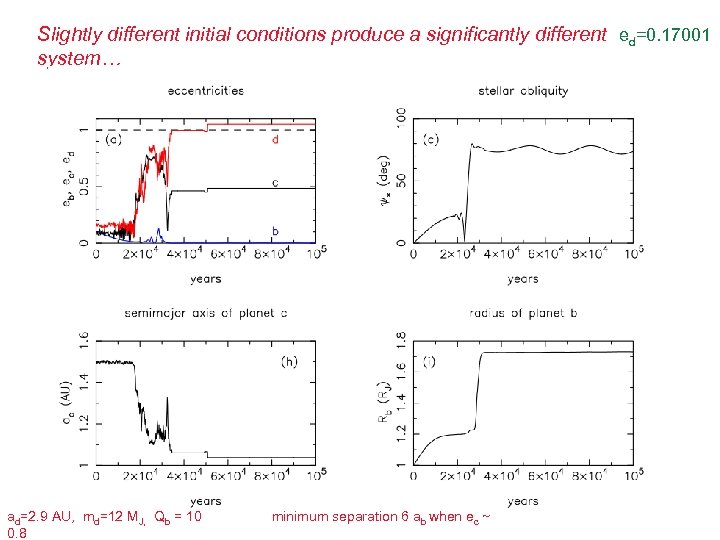Slightly different initial conditions produce a significantly different ed=0. 17001 system… ad=2. 9 AU, md=12 MJ, Qb = 10 0. 8 minimum separation 6 ab when ec ~

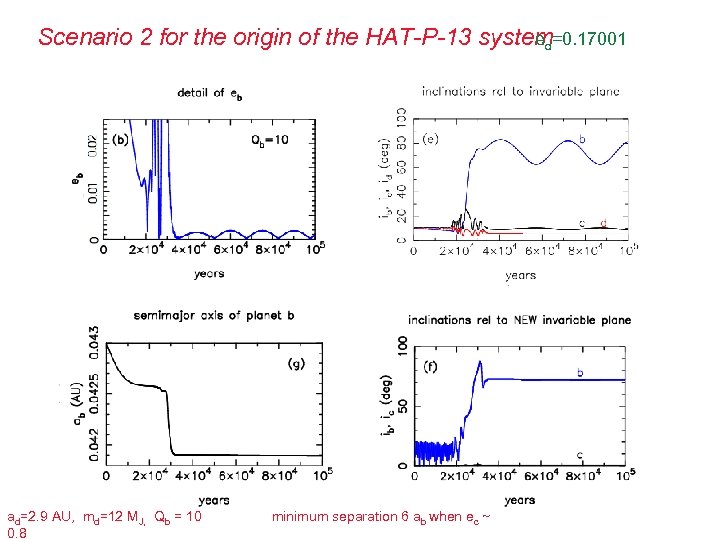Scenario 2 for the origin of the HAT-P-13 system=0. 17001 ed ad=2. 9 AU, md=12 MJ, Qb = 10 0. 8 minimum separation 6 ab when ec ~

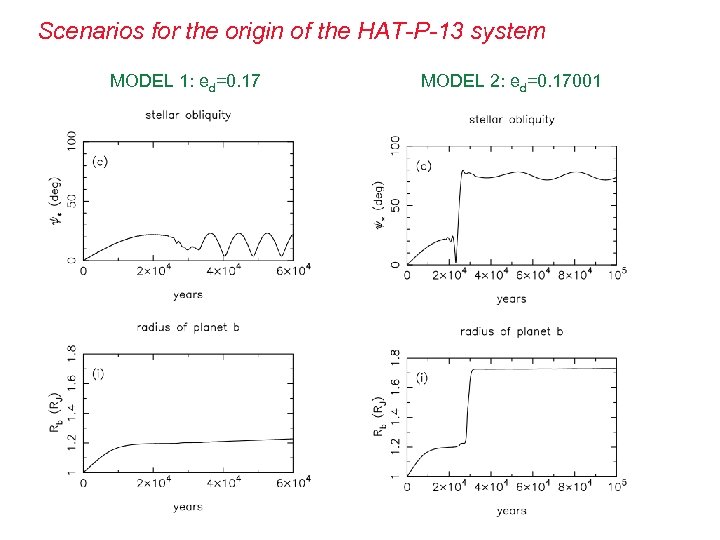Scenarios for the origin of the HAT-P-13 system MODEL 1: ed=0. 17 MODEL 2: ed=0. 17001

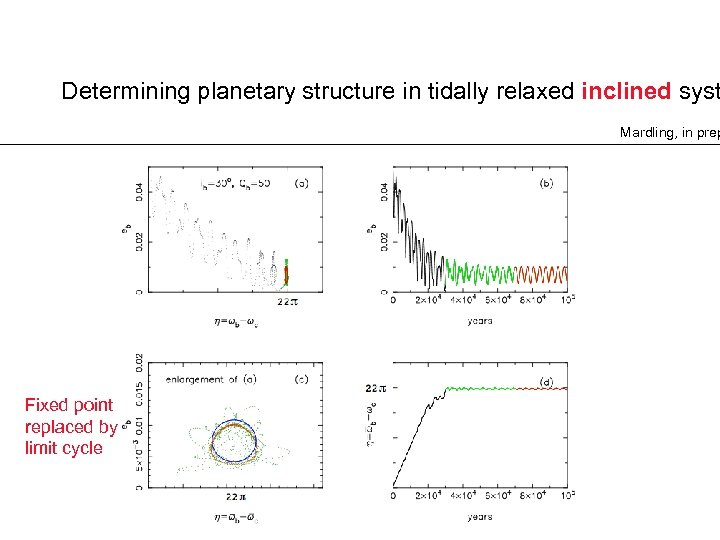Determining planetary structure in tidally relaxed inclined syst Mardling, in prep Fixed point replaced by limit cycle

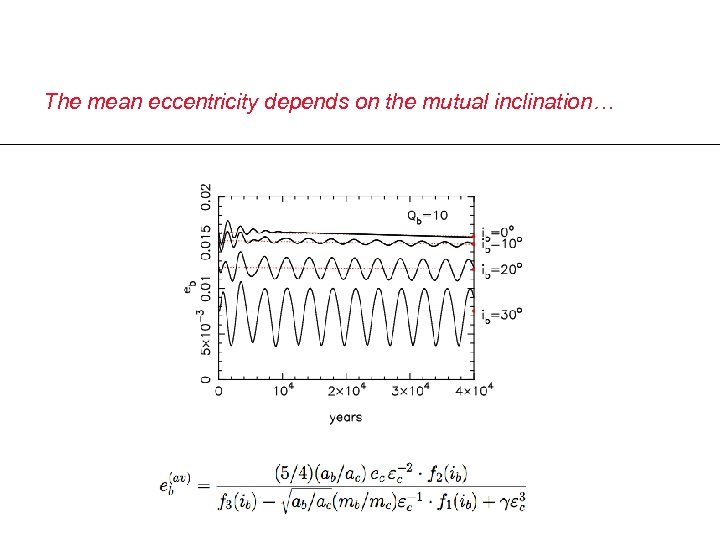The mean eccentricity depends on the mutual inclination…

Now a forced dynamical system - no fixed point solutions, only limit cycles b is the argument of periastron

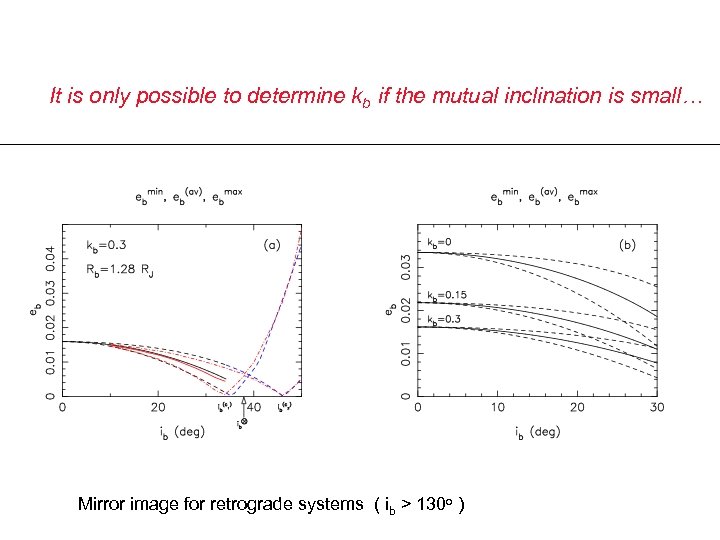It is only possible to determine kb if the mutual inclination is small… Mirror image for retrograde systems ( ib > 130 o )

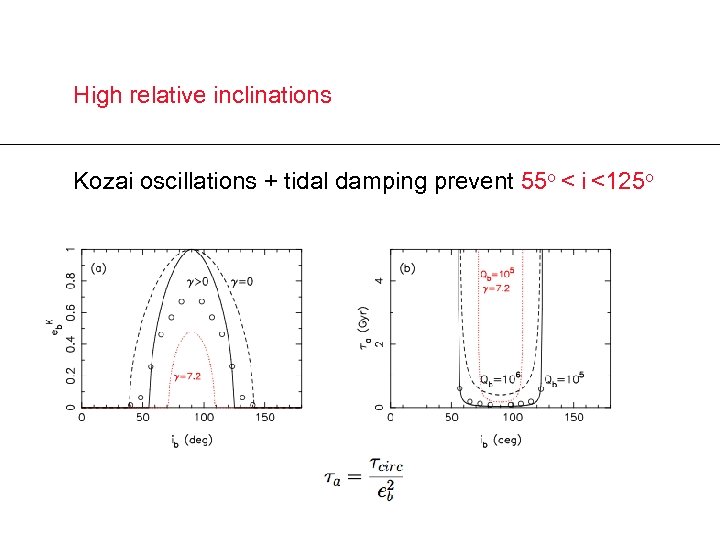High relative inclinations Kozai oscillations + tidal damping prevent 55 o < i <125 o

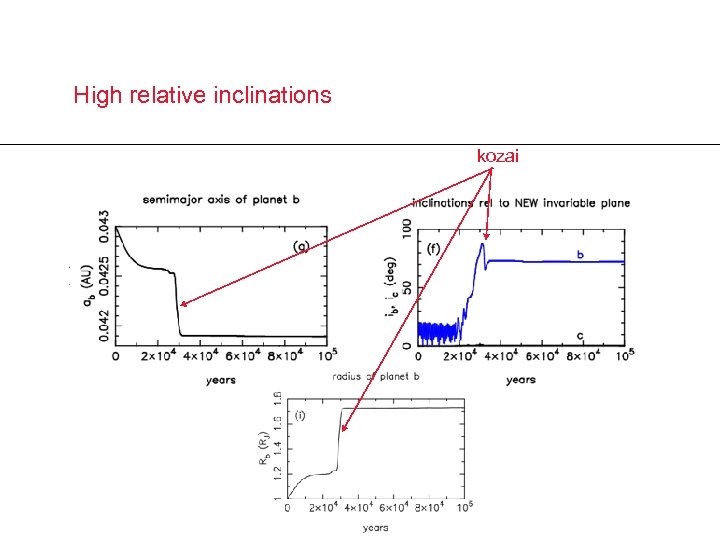High relative inclinations kozai

High relative inclinations Kozai oscillations + tidal damping prevent 55 o < i <125 o Prediction: HAT-P-13 b and c will not have a mutual inclination in this rang Mutual inclination can be estimated via transit-timing variations (TTVs) (Nesvorny 2009) If stellar obliquity rel to planet b i*b > 55 o stellar obliquity rel to planet c i*c > i*b-55 o Stellar obliquity measured via the Rossiter-Mc. Laughlin effect

retrograde planetary orbits 2009: two transiting exoplanet systems discovered to have retrograde orb 1. HAT-P-7 b (Hungarian Automated Telescopes : Cf. A) 2. WASP-17 b (Wide Angle Search for Planets: UK consortium)

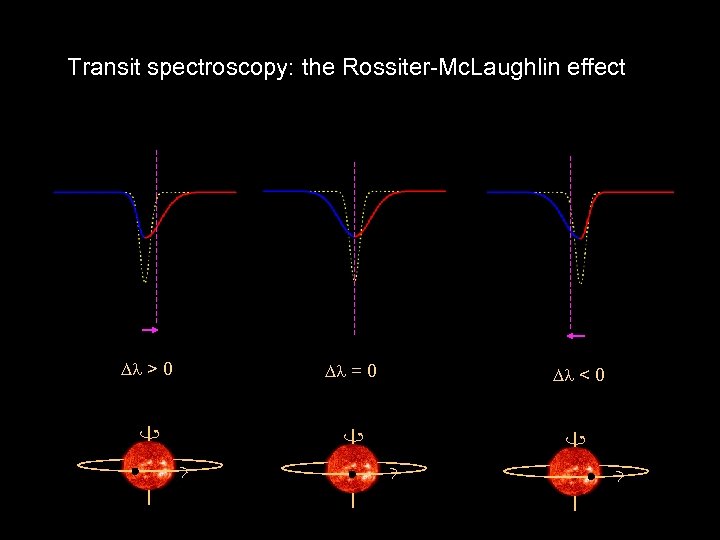Transit spectroscopy: the Rossiter-Mc. Laughlin effect > 0 = 0 < 0

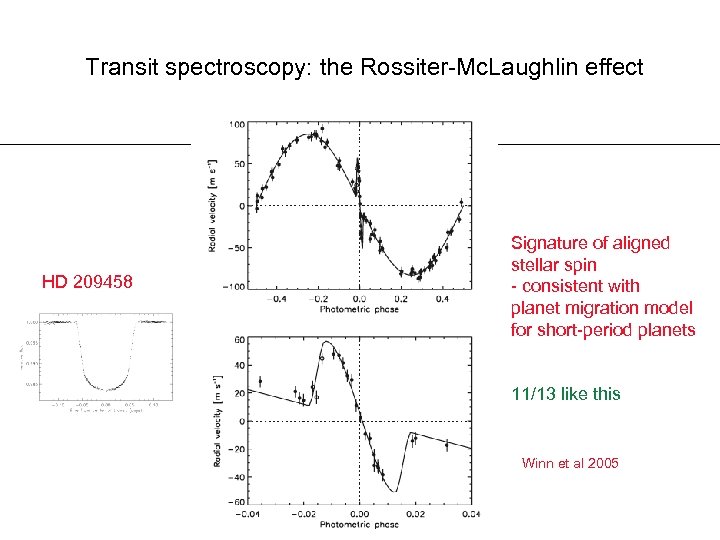Transit spectroscopy: the Rossiter-Mc. Laughlin effect HD 209458 Signature of aligned stellar spin - consistent with planet migration model for short-period planets 11/13 like this Winn et al 2005

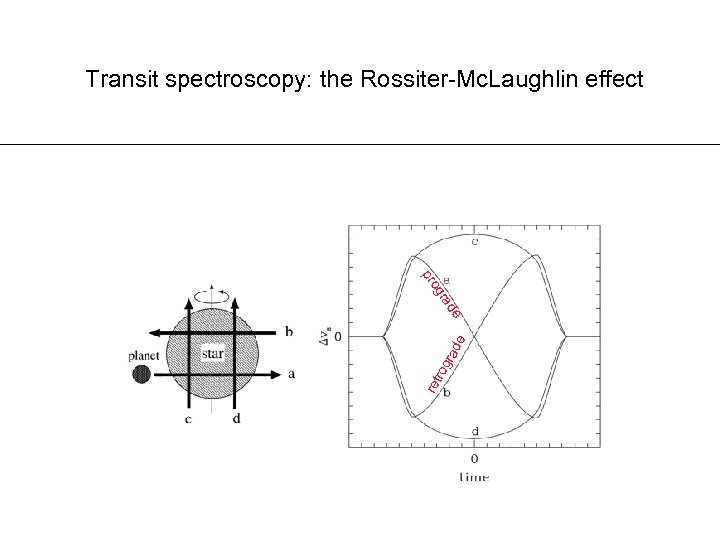Transit spectroscopy: the Rossiter-Mc. Laughlin effect ret r og rad e de ra og pr

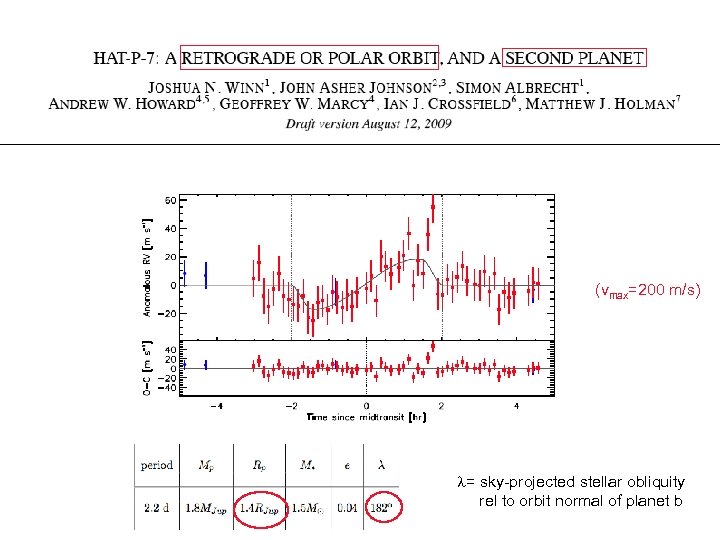(vmax=200 m/s) = sky-projected stellar obliquity rel to orbit normal of planet b

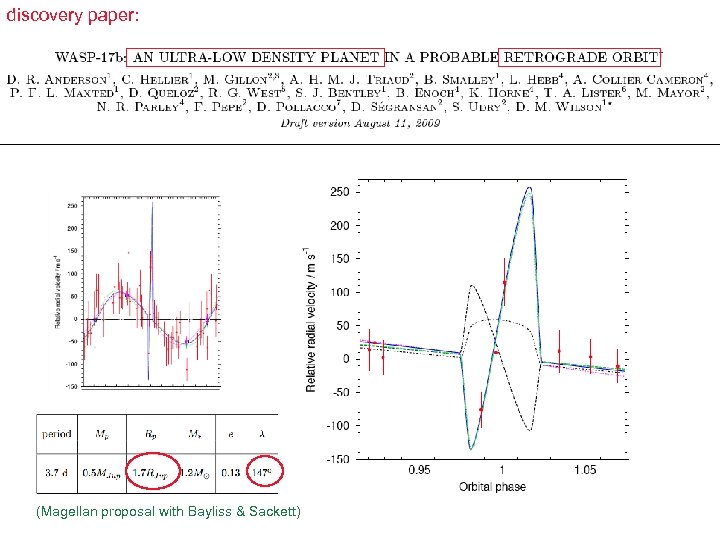discovery paper: (Magellan proposal with Bayliss & Sackett)

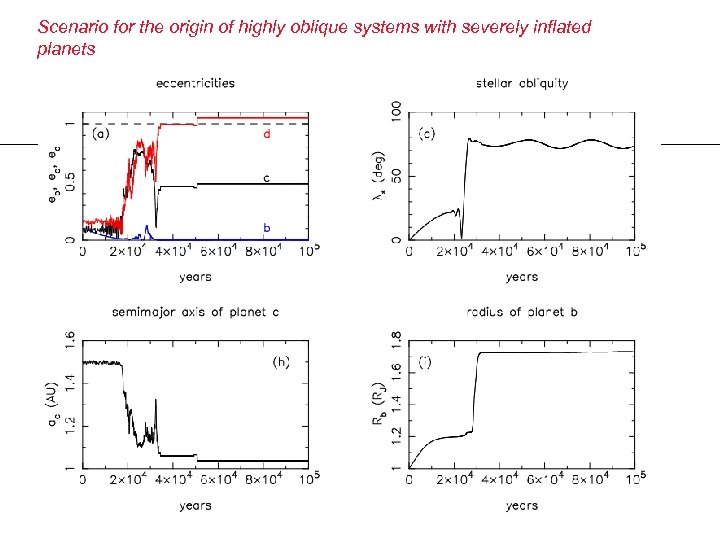Scenario for the origin of highly oblique systems with severely inflated planets