Designing a Solenoid for Low Temperature Resistance Measurements

Designing a Solenoid for Low Temperature Resistance Measurements of Nanostructures PHYS 4300 May 15, 2009 Jon Caddell Dr. Murphy

Outline • Motivation • Spintronics • Weak Localization • Minimizing Spatial Variation of Resistance • Laboratory Details • Current Experimental Setup • New Setup (add Independent Perpendicular Field) • Modeling B Field Spatial Variation • Non-infinite Solenoid B Field Non-uniformities • Conclusion • Optimizing Solenoid Design to Minimize Spatial Variation of Resistance

Spintronics • Digital technology has two states corresponding to logic True/False • If the parameters associated with spin are included, then you can double the number of logic states • Go from binary computing to four-level logic computing (T/F T↑ /T↓ /F↑ /F↓ ) • This could boost computing power (more information stored per bit) • In. Sb interesting for spintronics; need to know more about fundamental spin behavior

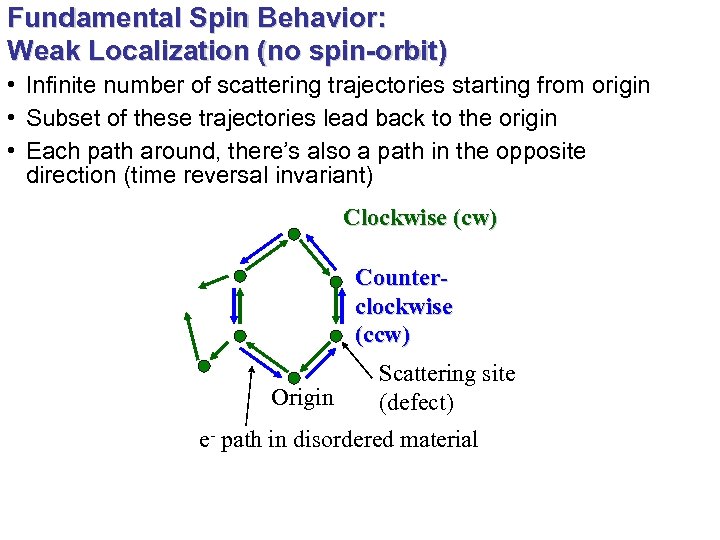Fundamental Spin Behavior: Weak Localization (no spin-orbit) • Infinite number of scattering trajectories starting from origin • Subset of these trajectories lead back to the origin • Each path around, there’s also a path in the opposite direction (time reversal invariant) Clockwise (cw) Counterclockwise (ccw) Origin Scattering site (defect) e- path in disordered material

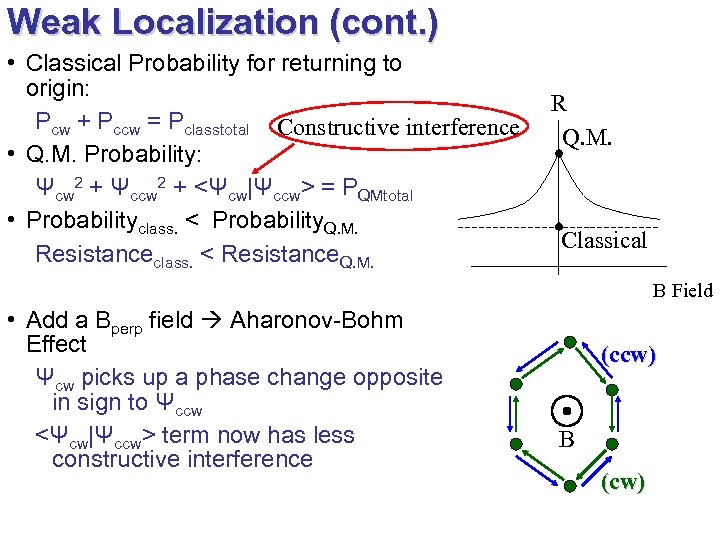Weak Localization (cont. ) • Classical Probability for returning to origin: Pcw + Pccw = Pclasstotal Constructive interference • Q. M. Probability: Ψcw 2 + Ψccw 2 + <Ψcw|Ψccw> = PQMtotal • Probabilityclass. < Probability. Q. M. Resistanceclass. < Resistance. Q. M. R Q. M. Classical B Field • Add a Bperp field Aharonov-Bohm Effect Ψcw picks up a phase change opposite in sign to Ψccw <Ψcw|Ψccw> term now has less constructive interference (ccw) B (cw)

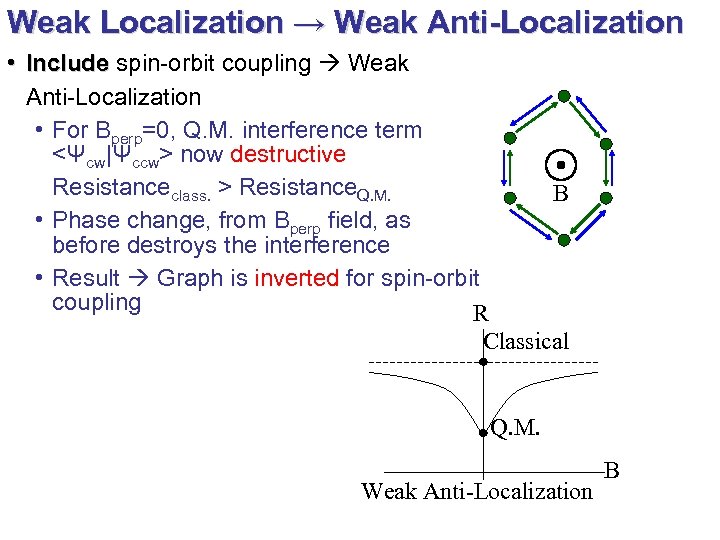Weak Localization → Weak Anti-Localization • Include spin-orbit coupling Weak Anti-Localization • For Bperp=0, Q. M. interference term <Ψcw|Ψccw> now destructive Resistanceclass. > Resistance. Q. M. B • Phase change, from Bperp field, as before destroys the interference • Result Graph is inverted for spin-orbit coupling R Classical Q. M. Weak Anti-Localization B

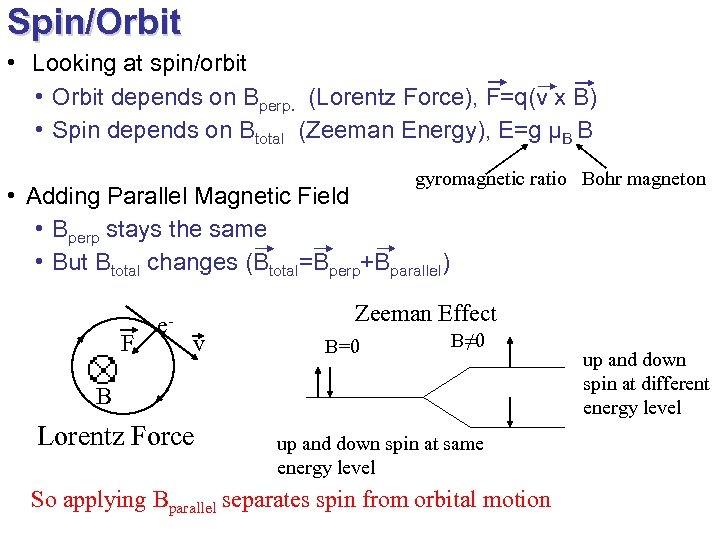Spin/Orbit • Looking at spin/orbit • Orbit depends on Bperp. (Lorentz Force), F=q(v x B) • Spin depends on Btotal (Zeeman Energy), E=g µB B gyromagnetic ratio Bohr magneton • Adding Parallel Magnetic Field • Bperp stays the same • But Btotal changes (Btotal=Bperp+Bparallel) F e- Zeeman Effect v B=0 B≠ 0 B Lorentz Force up and down spin at same energy level So applying Bparallel separates spin from orbital motion up and down spin at different energy level

Weak Anti-Localization and Bll Magnetic Field • One spin energetically favorable So applying Bparallel separates spin from orbital motion • Goal: seeing how weak anti-localization changes with magnetic field Zeeman Effect B=0 B≠ 0 R Classical Q. M. up and down spin at same energy level up and down spin at different energy level Weak Anti-Localization

Outline • Motivation • Spintronics • Weak Localization • Minimizing Resistance Spatial Variation • Background • Current Experimental Setup • New Setup (add Independent Perpendicular Field) • Modeling B Field Spatial Variation • Non-infinite Solenoid B Field Non-uniformities • Conclusion

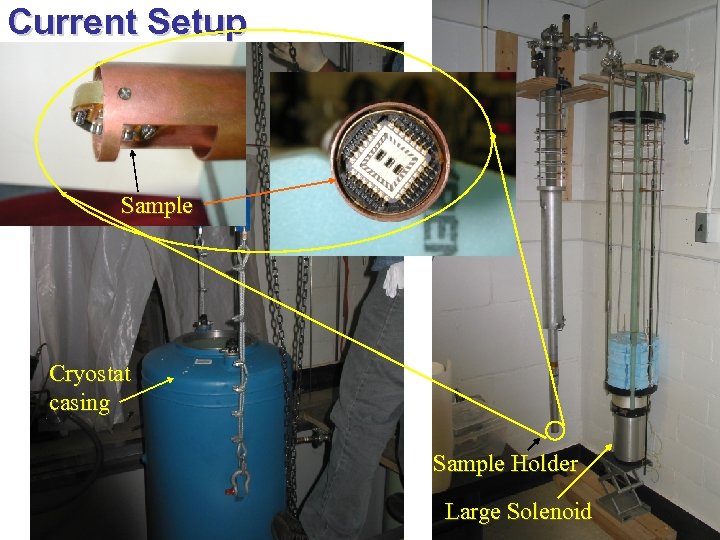Current Setup Sample Cryostat casing Sample Holder Large Solenoid

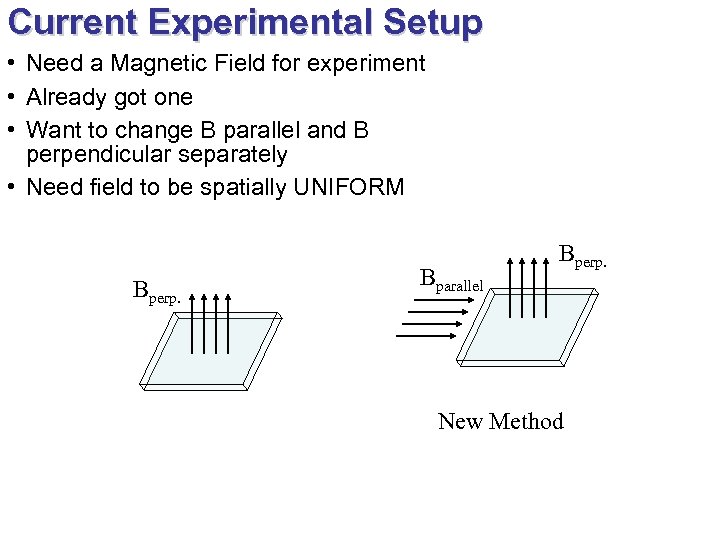Current Experimental Setup • Need a Magnetic Field for experiment • Already got one • Want to change B parallel and B perpendicular separately • Need field to be spatially UNIFORM Bperp. Bparallel Bperp. New Method

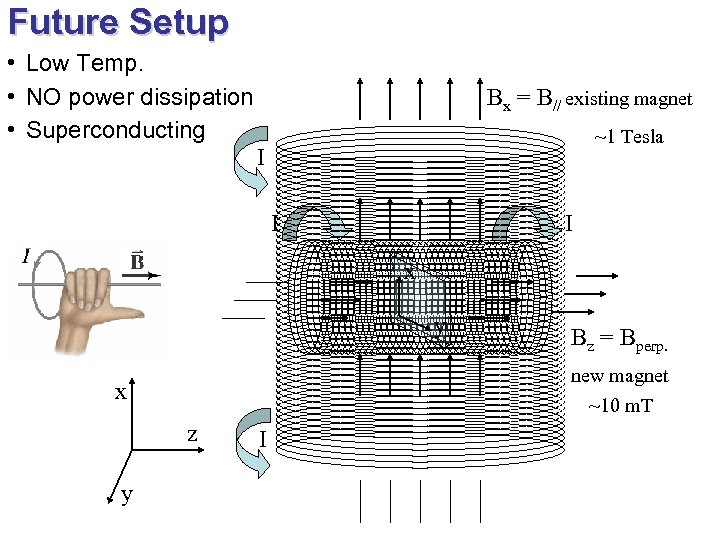Future Setup • Low Temp. • NO power dissipation • Superconducting Bx = B// existing magnet ~1 Tesla I I I x y new magnet ~10 m. T x z y Bz = Bperp. I

Manufacturability, Economics, Environmental, Safety • Manufacturability • Materials: order off-the-shelf Nb. Ti wire, machine the coil form and wind coil ourselves, pot in standard epoxy • Constraints: solenoid must fit inside 2” diameter larger solenoid (limits length and diameter), wire diameter from what is commercially available • Economics • Coil design and construction in-house to avoid outside custom work • Environmental • No power dissipation since coil is superconducting; materials recyclable (except epoxy) and non-toxic

Manufacturability, Economics, Environmental, Safety • Safety – Cryogenic Temp. • Quench Protection P=VI=0 superconducting, IIc Power dissipation → boil He (liquid → gas) Expands x 700 • Quench valve, open to relieve over-pressure • Air content • Air 22% O 2 if a quench, lots of He, O 2 content drop Evacuate room.

Outline • Motivation • Spintronics • Weak Localization • Minimizing Resistance Spatial Variation • Background • Current Experimental Setup • New Setup (add Independent Perpendicular Field) • Modeling B Field Spatial Variation • Non-infinite Solenoid B Field Non-uniformities • Conclusion

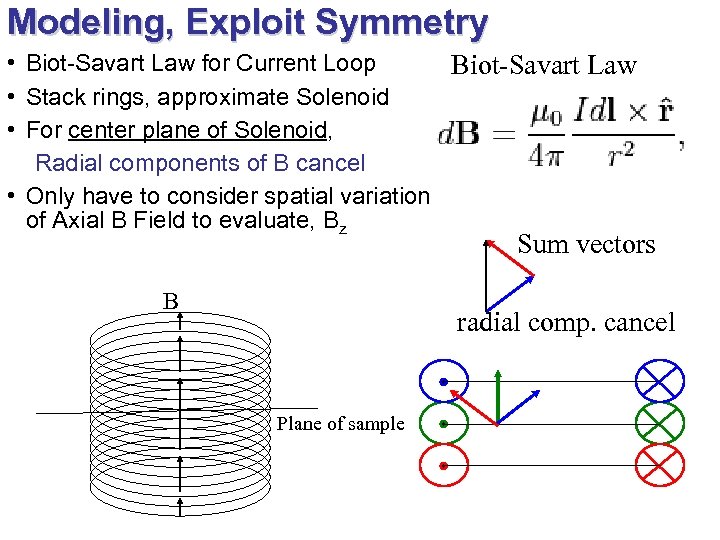Modeling, Exploit Symmetry • Biot-Savart Law for Current Loop Biot-Savart Law • Stack rings, approximate Solenoid • For center plane of Solenoid, Radial components of B cancel • Only have to consider spatial variation of Axial B Field to evaluate, Bz Sum vectors B radial comp. cancel Plane of sample

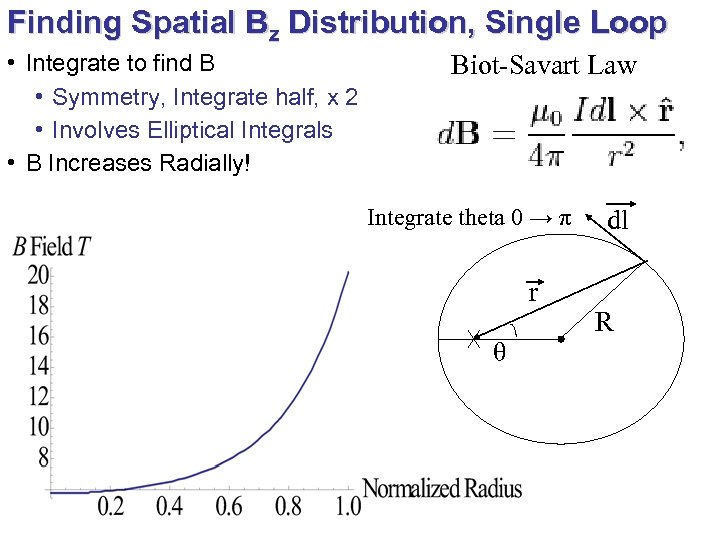Finding Spatial Bz Distribution, Single Loop • Integrate to find B • Symmetry, Integrate half, x 2 • Involves Elliptical Integrals • B Increases Radially! Biot-Savart Law Integrate theta 0 → π r θ dl R

Modeling Solenoid • Method A: Summing stacked current loops Uses Elliptical Integrals Elliptic Integral of the first kind Elliptic Integral of the second kind

Modeling Solenoid • Method B: Solenoid Model Uses Legendre Polynomials Previous citation &

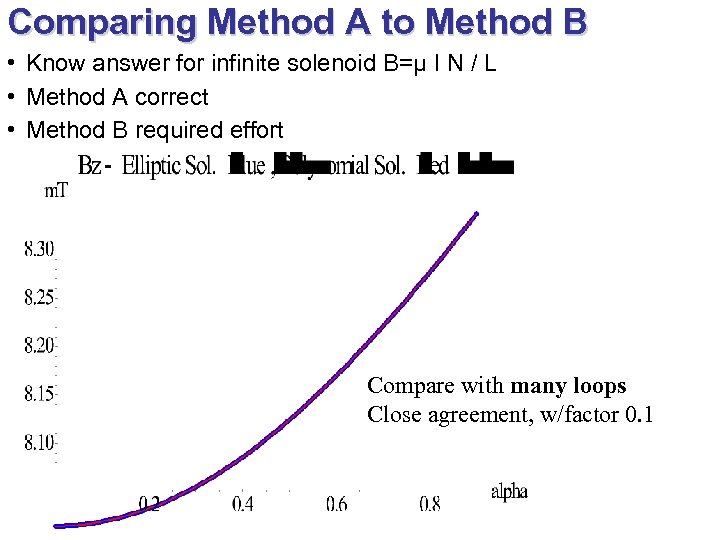Comparing Method A to Method B • Know answer for infinite solenoid B=µ I N / L • Method A correct • Method B required effort Compare with many loops Close agreement, w/factor 0. 1

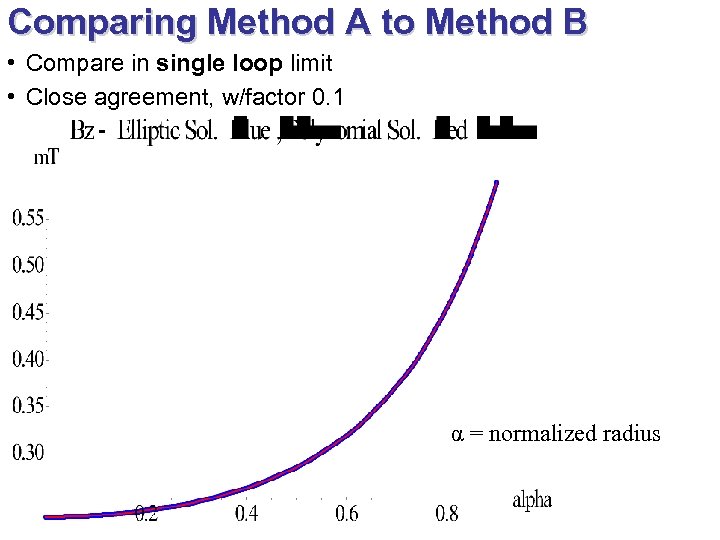Comparing Method A to Method B • Compare in single loop limit • Close agreement, w/factor 0. 1 α = normalized radius

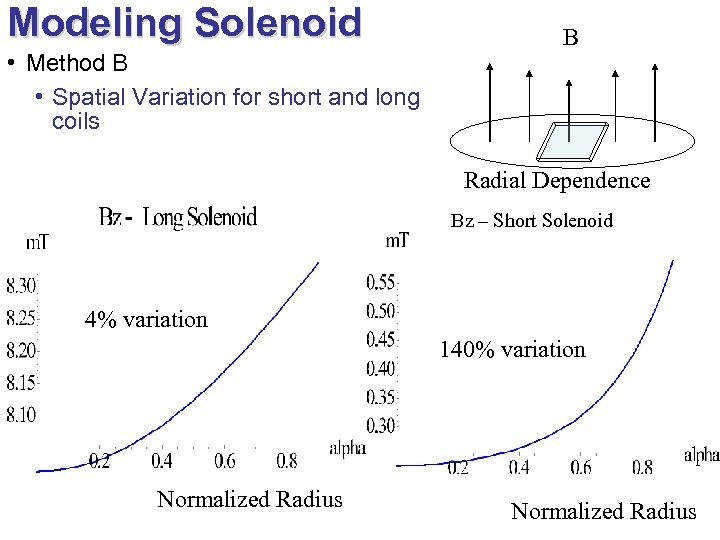Modeling Solenoid • Method B • Spatial Variation for short and long coils B Radial Dependence Bz – Short Solenoid 4% variation 140% variation Normalized Radius

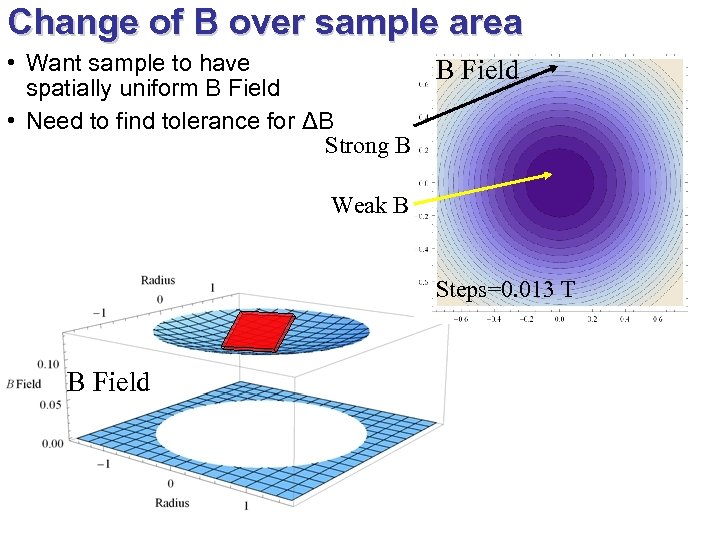Change of B over sample area • Want sample to have spatially uniform B Field • Need to find tolerance for ΔB Strong B B Field Weak B Steps=0. 013 T B Field

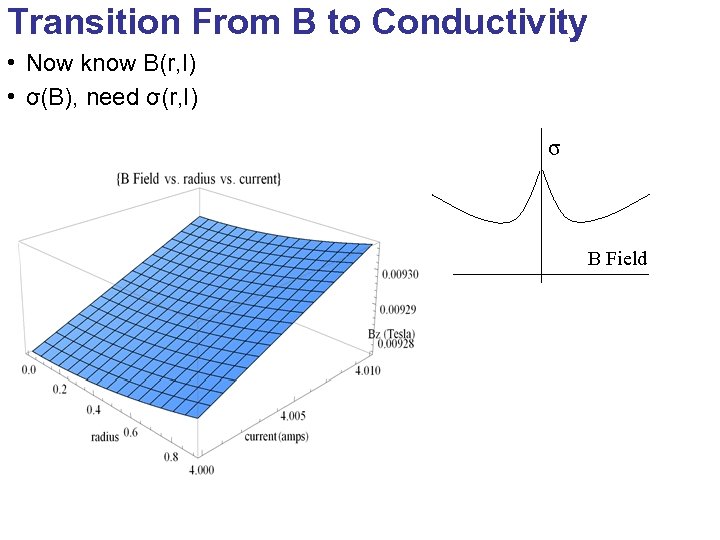Transition From B to Conductivity • Now know B(r, I) • σ(B), need σ(r, I) σ B Field

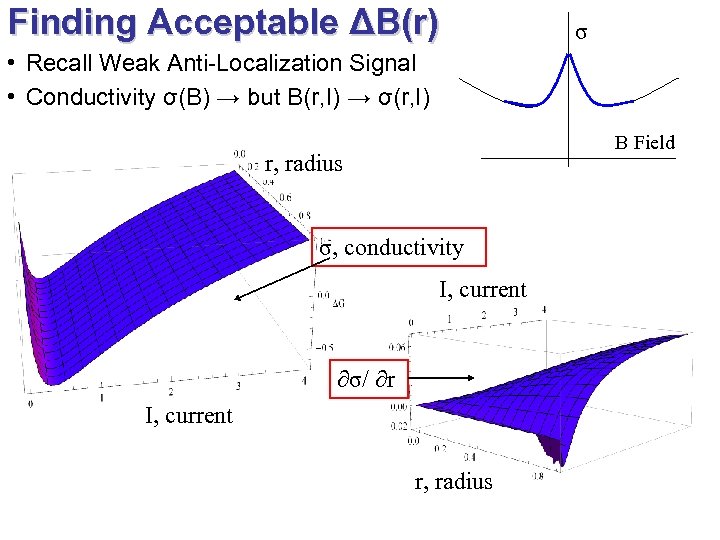Finding Acceptable ΔB(r) σ • Recall Weak Anti-Localization Signal • Conductivity σ(B) → but B(r, I) → σ(r, I) B Field r, radius σ, conductivity I, current ∂σ/ ∂r I, current r, radius

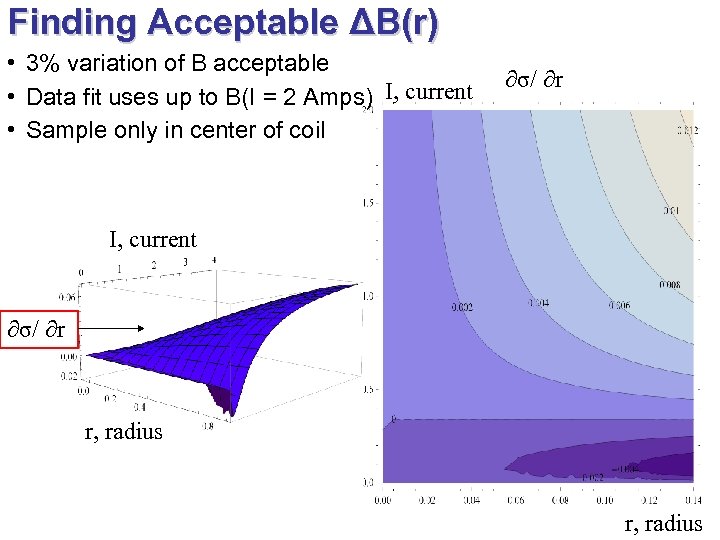Finding Acceptable ΔB(r) • 3% variation of B acceptable • Data fit uses up to B(I = 2 Amps) I, current • Sample only in center of coil ∂σ/ ∂r I, current ∂σ/ ∂r r, radius

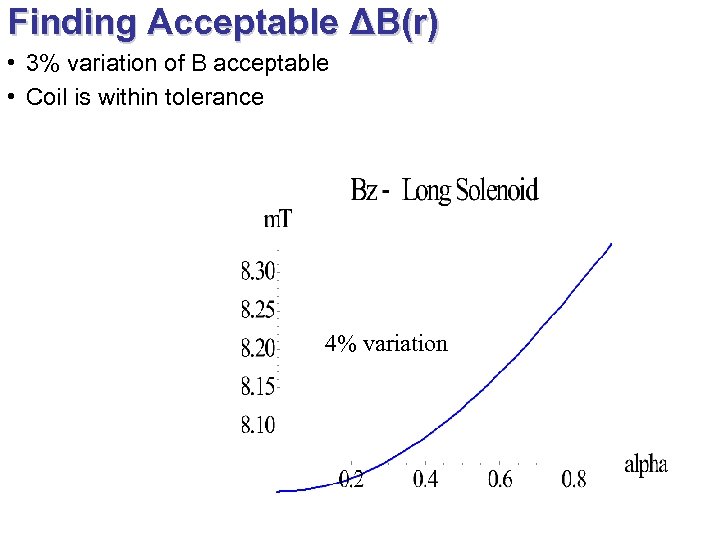Finding Acceptable ΔB(r) • 3% variation of B acceptable • Coil is within tolerance 4% variation

Trends of Field on Center B(coil dia. ) B(wire dia. ) B(length) B(coil dia. &length coupled)

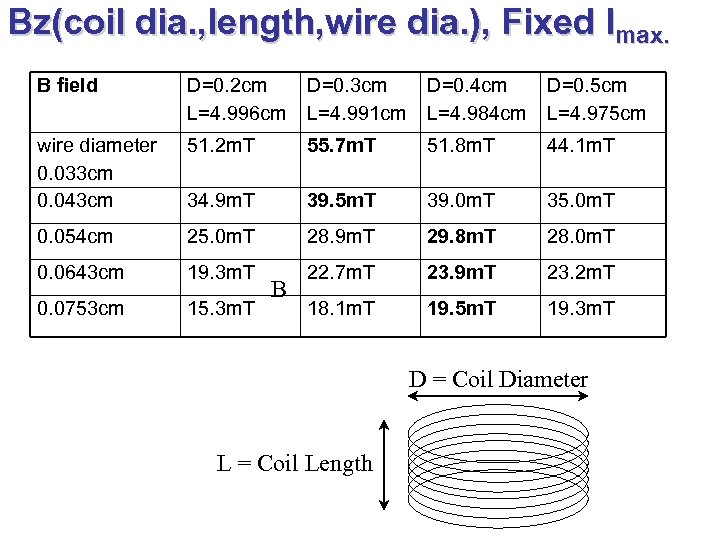Bz(coil dia. , length, wire dia. ), Fixed Imax. B field D=0. 2 cm L=4. 996 cm D=0. 3 cm L=4. 991 cm D=0. 4 cm L=4. 984 cm D=0. 5 cm L=4. 975 cm wire diameter 0. 033 cm 0. 043 cm 51. 2 m. T 55. 7 m. T 51. 8 m. T 44. 1 m. T 34. 9 m. T 39. 5 m. T 39. 0 m. T 35. 0 m. T 0. 054 cm 25. 0 m. T 28. 9 m. T 29. 8 m. T 28. 0 m. T 0. 0643 cm 19. 3 m. T 22. 7 m. T 23. 9 m. T 23. 2 m. T 0. 0753 cm 15. 3 m. T 18. 1 m. T 19. 5 m. T 19. 3 m. T B D = Coil Diameter L = Coil Length

Conclusion • Steps • Mathematica Routine to model B Field • Optimize Field by minimizing B variations • Design superconducting coil • Future Steps • Build superconducting coil • Test at cryogenic temperatures (4. 2 K) • Perform Measurements

References Sources for Formulas: Elliptical Integral, Legendre Polynomial from: • SOME USEFUL INFORMATION FOR THE DESIGN OF AIR-CORE SOLENOIDS by D. Bruce Montgomery and J. Terrell. , published November, 1961, under Air Force Contract AF 19(604)-7344. • Dimensionless Prefactor from: • THE DESIGN OF POWERFUL ELECTROMAGNETS: Part II. The Magnetizing Coil, by F. Bitter, published December 1936, R. S. I. Vol. 7 • Current Setup pictures courtesy of Ruwan Dedigama

Acknowledgements • Dr. Murphy, Capstone Advisor • Ruwan Dedigama, Graduate Student • Dilhani Jayathilaka, Graduate Student