Design of Open Channels and Culverts CE 453

Design of Open Channels and Culverts CE 453 Lecture 26 Ref: Chapter 17 of your text and HYDRAULIC DESIGN OF HIGHWAY CULVERTS, Hydraulic Design Series Number 5, Federal Highway Administration, Publication No. FHWA-NHI-01 -020, September 2001; available at http: //www. cflhd. gov/design/hyd/hds 5_03 r. pdf, accessed March 18, 2006

Design of Open Channels

Longitudinal Slopes n Gradient longitudinal direction of highway to facilitate movement of water along roadway

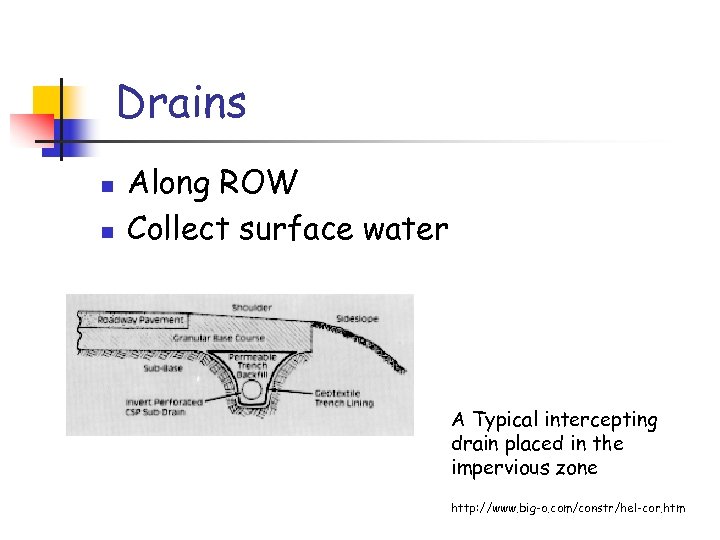Drains n n Along ROW Collect surface water A Typical intercepting drain placed in the impervious zone http: //www. big-o. com/constr/hel-cor. htm

Drainage Channels (Ditches) Design l l l Adequate capacity Minimize hazard to traffic Hydraulic efficiency Ease of maintenance Desirable design (for safety): flat slopes, broad bottom, and liberal rounding

Ditch Shape Source: Fabriform 1. com l l Trapezoidal – generally preferred considering hydraulics, maintenance, and safety V-shaped – less desirable from safety point of view and maintenance

Terms Steady Flow: rate of discharge does not vary with time (Manning’s applies) Uniform: channel properties are constant along length of channel Slope Roughness Cross-section Water surface is parallel to slope of channel Non-uniform: properties vary

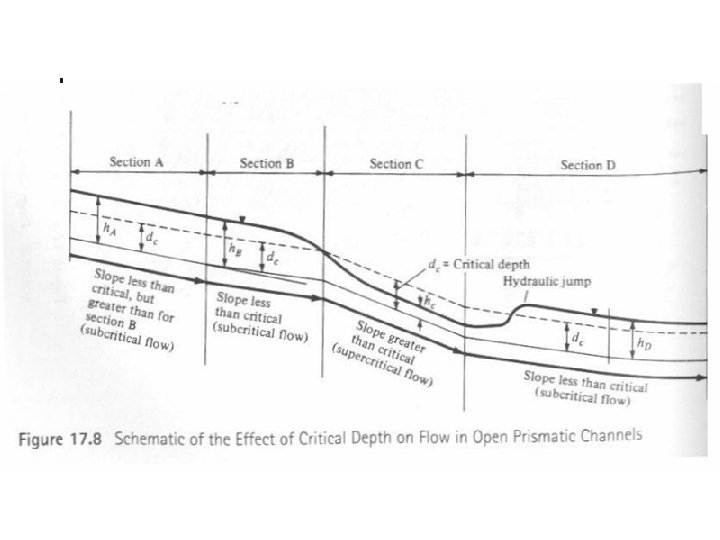
Terms Unsteady flow: rate of discharge varies with time Critical depth a hydraulic control in design depth of water where flow changes from tranquil to rapid/shooting Critical velocity: velocity corresponding to critical depth Critical slope: slope corresponding to critical depth

Flow Velocity • • Depends on lining type Should be high enough to prevent deposit of transported material (sedimentation) • • For most linings, problem if S < 1% Should be low enough to prevent erosion (scour) • For most types of linings, problem if S > 5%

Use spillway or chute if Δelev is large

Rip Rap for drainage over high slope

Riprap (TN Design Manual)

Side Ditch/Open Channel Design-Basics • • Find expected Q at point of interest (see previous lecture) Select a cross section for the slope, and any erosion control needed Manning’s formula used for design Assume steady flow in a uniform channel

Manning’s Formula V = R 2/3*S 1/2 n (metric) V = 1. 486 R 2/3*S 1/2 n where: V = mean velocity (m/sec or ft/sec) R = hydraulic radius (m, ft) = area of the cross section of flow (m 2, ft 2) divided by wetted perimeter (m, f) S = slope of channel n = Manning’s roughness coefficient

Side Ditch/Open Channel Design-Basics Q = VA Q = discharge (ft 3/sec, m 3/sec) A = area of flow cross section (ft 2, m 2) FHWA has developed charts to solve Manning’s equation for different cross sections

Open Channel Example n n n Runoff = 340 ft 3/sec (Q) Slope = 1% Manning’s # = 0. 015 Determine necessary cross-section to handle estimated runoff Use rectangular channel 6 -feet wide

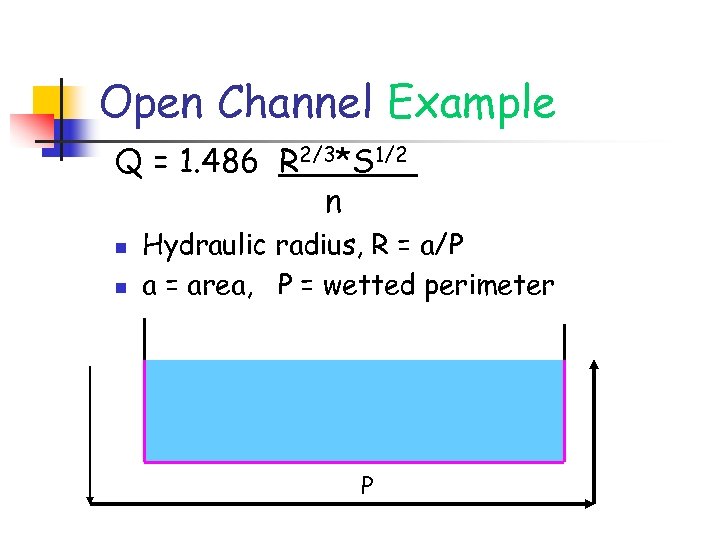Open Channel Example Q = 1. 486 R 2/3*S 1/2 n n n Hydraulic radius, R = a/P a = area, P = wetted perimeter P

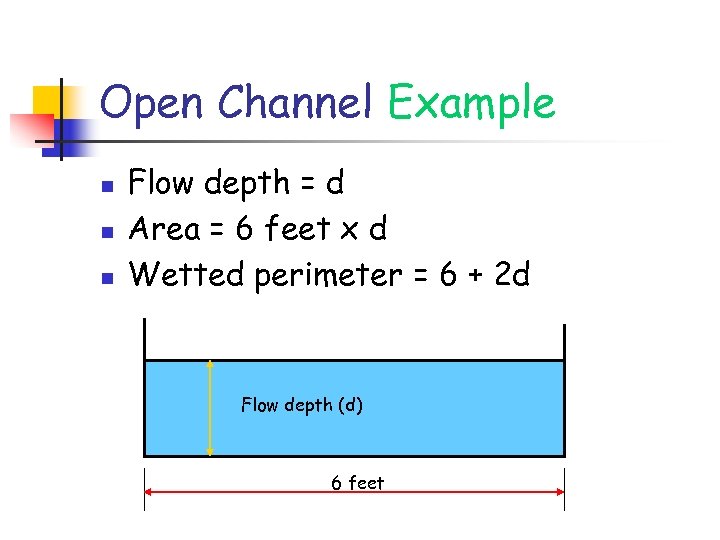Open Channel Example n n n Flow depth = d Area = 6 feet x d Wetted perimeter = 6 + 2 d Flow depth (d) 6 feet

Example (continued) Q = 1. 486 a R 2/3*S 1/2 n 340 ft 3/sec = 1. 486 (6 d)2/3 (0. 01)1/2 (6 + 2 d) 0. 015 d 4 feet Channel area needs to be at least 4’ x 6’

Example (continued) Find flow velocities. V = 1. 486 R 2/3*S 1/2 n with R = a/P = 6 ft x 4 ft = 1. 714 2(4 ft) + 6 ft so, V = 1. 486(1. 714)2/3 (0. 01)1/2 = 14. 2 ft/sec 0. 015 If you already know Q, simpler just to do V=Q/A = 340/24 = 14. 2)

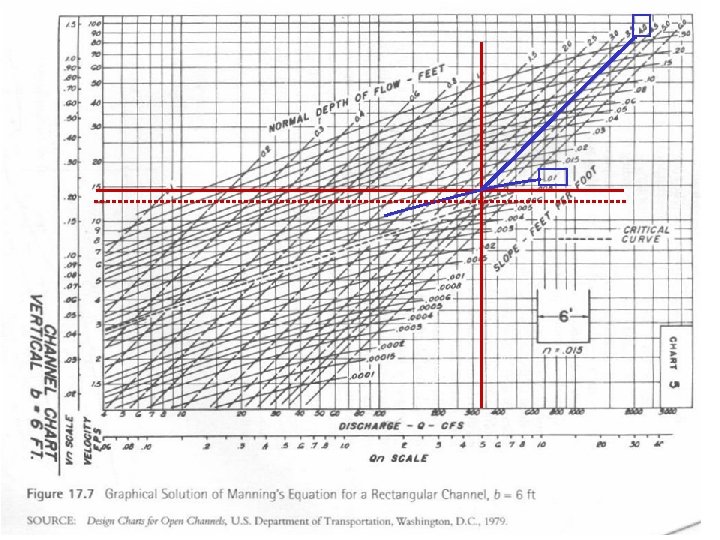
Example (continued) Find critical velocities. From chart along critical curve, vc 13 ft/sec Critical slope = 0. 007 Find critical depth: yc = (q 2/g)1/3 g = 32. 2 ft/sec 2 q = flow per foot of width = 340 ft 3/sec /6 feet = 56. 67 ft 2/sec yc = (56. 672/32. 2)1/3 = 4. 64 feet > depth of 4’

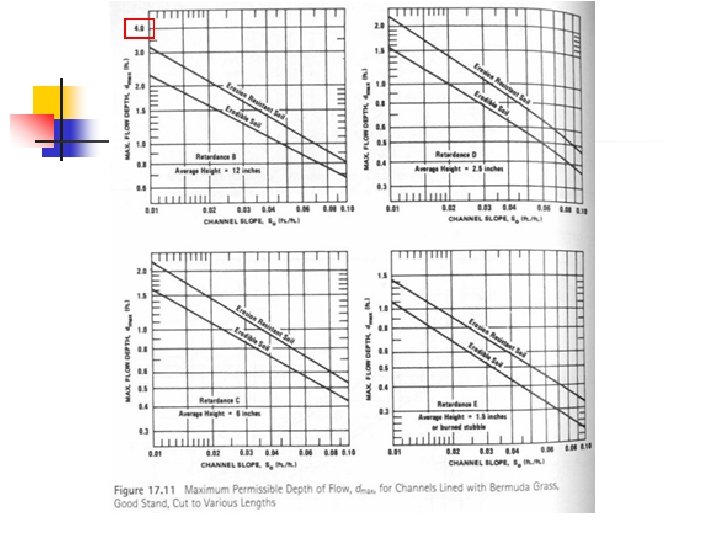
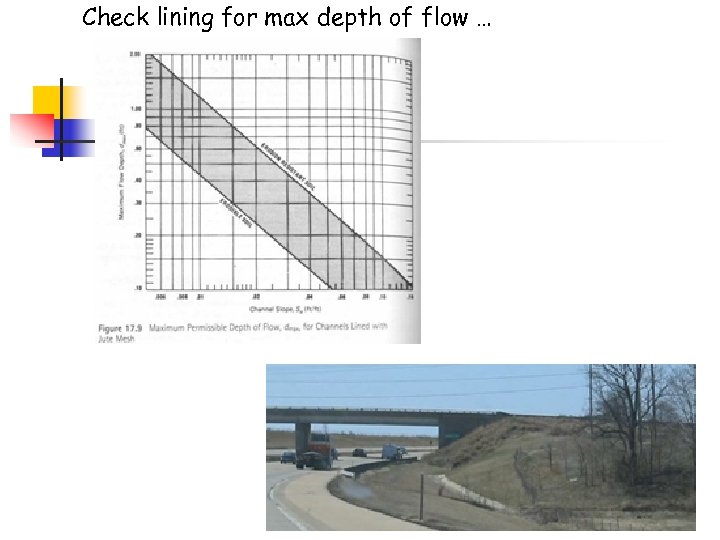Check lining for max depth of flow …

Rounded

A cut slope with ditch

A fill slope

Inlet or drain marker

Ditch treatment near a bridge US 30 – should pier be protected?

A fill slope

Hidden Drain Where’s the water going to end up?

Median drain

Design of Culverts Source: Michigan Design Manual

Culvert Design - Basics l l l Top of culvert not used as pavement surface (unlike bridge), usually less than 20 foot span > 20 feet use a bridge Three locations l l l Bottom of Depression (no watercourse) Natural stream intersection with roadway (Majority) Locations where side ditch surface drainage must cross roadway

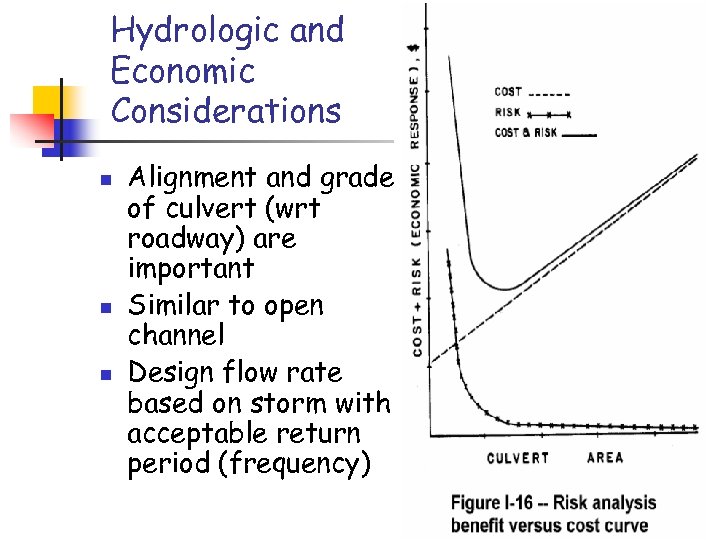Hydrologic and Economic Considerations n n n Alignment and grade of culvert (wrt roadway) are important Similar to open channel Design flow rate based on storm with acceptable return period (frequency)

Culvert Design Steps l l Obtain site data and roadway cross section at culvert crossing location (with approximation of stream elevation) – best is natural stream location and slope (may be expensive though) Establish inlet/outlet elevations, length, and slope of culvert

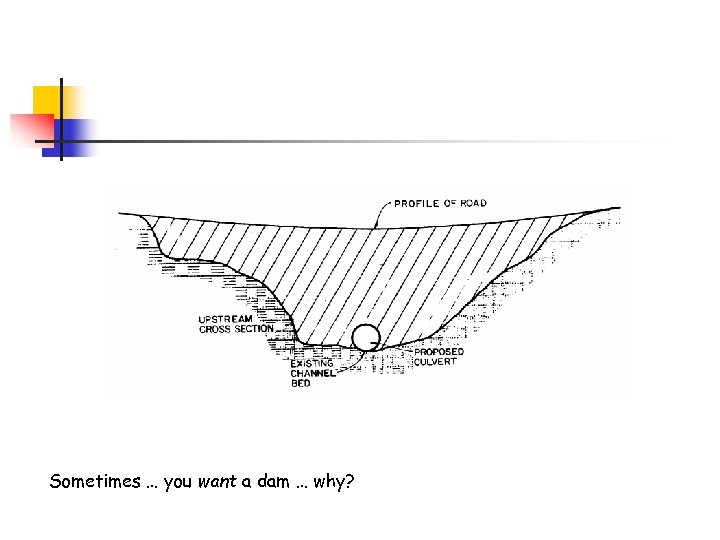Sometimes … you want a dam … why?

Culvert Design Steps l l l Determine allowable headwater depth (and probable tailwater depth) during design flood – control on design size – f(topography and nearby land use) Select type and size of culvert Examine need for energy dissipaters

Headwater Depth n n n Constriction due to culvert creates increase in depth of water just upstream Allowable/desirable level of headwater upstream usually controls culvert size and inlet geometry Allowable headwater depth depends on topography and land use in immediate vicinity

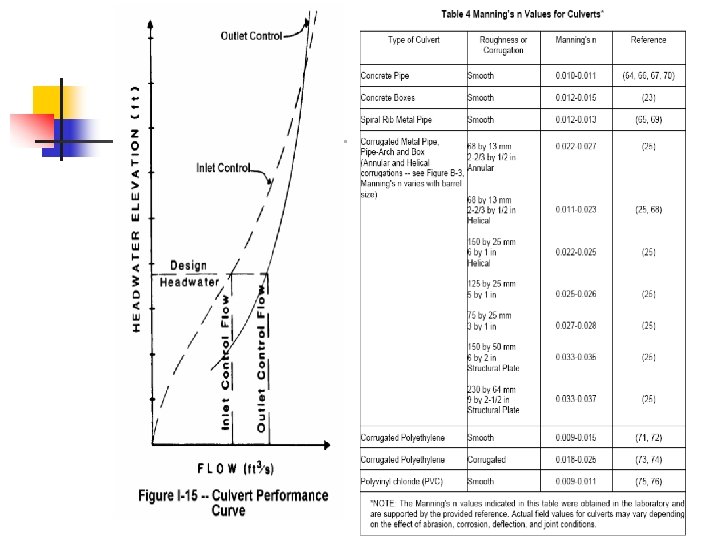
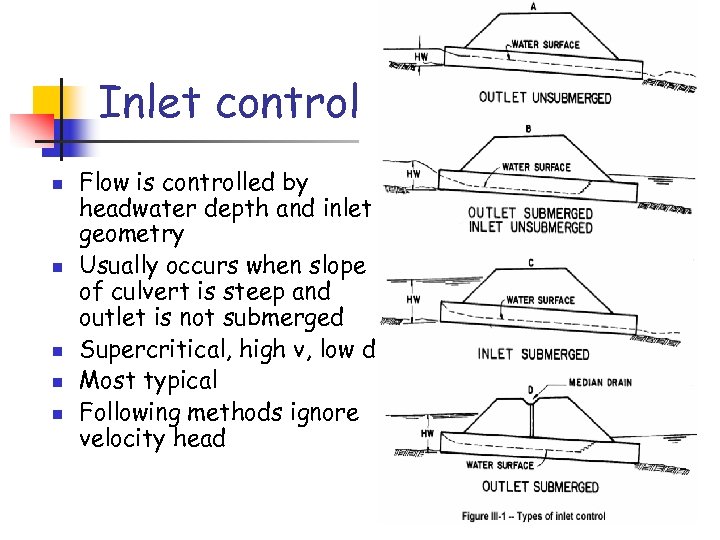Inlet control n n n Flow is controlled by headwater depth and inlet geometry Usually occurs when slope of culvert is steep and outlet is not submerged Supercritical, high v, low d Most typical Following methods ignore velocity head

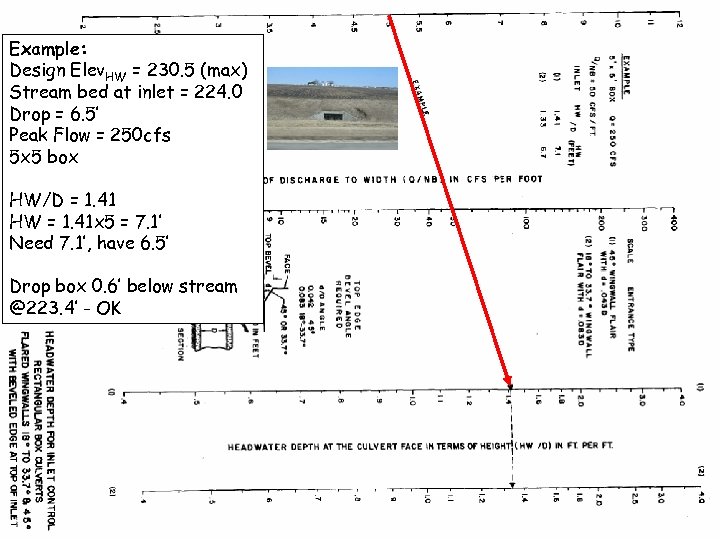Example: Design Elev. HW = 230. 5 (max) Stream bed at inlet = 224. 0 Drop = 6. 5’ Peak Flow = 250 cfs 5 x 5 box HW/D = 1. 41 HW = 1. 41 x 5 = 7. 1’ Need 7. 1’, have 6. 5’ Drop box 0. 6’ below stream @223. 4’ - OK

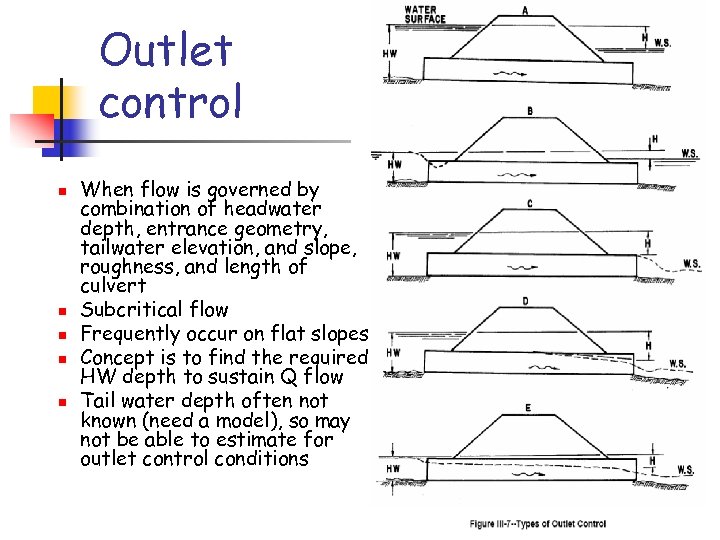Outlet control n n n When flow is governed by combination of headwater depth, entrance geometry, tailwater elevation, and slope, roughness, and length of culvert Subcritical flow Frequently occur on flat slopes Concept is to find the required HW depth to sustain Q flow Tail water depth often not known (need a model), so may not be able to estimate for outlet control conditions

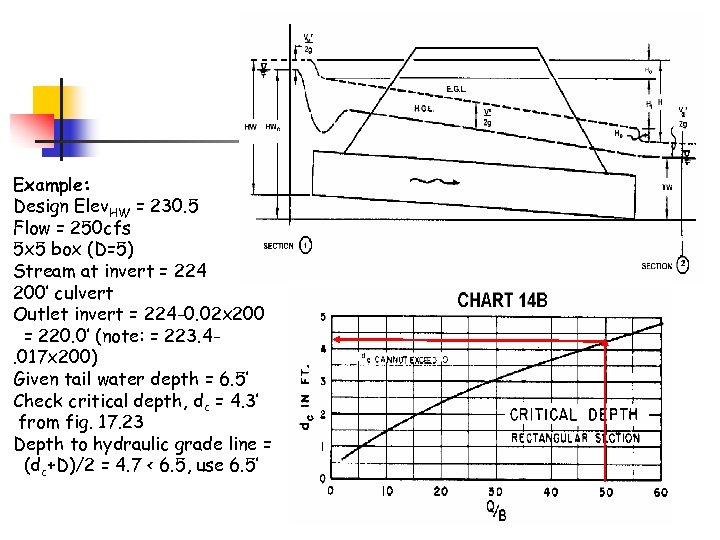Example: Design Elev. HW = 230. 5 Flow = 250 cfs 5 x 5 box (D=5) Stream at invert = 224 200’ culvert Outlet invert = 224 -0. 02 x 200 = 220. 0’ (note: = 223. 4. 017 x 200) Given tail water depth = 6. 5’ Check critical depth, dc = 4. 3’ from fig. 17. 23 Depth to hydraulic grade line = (dc+D)/2 = 4. 7 < 6. 5, use 6. 5’

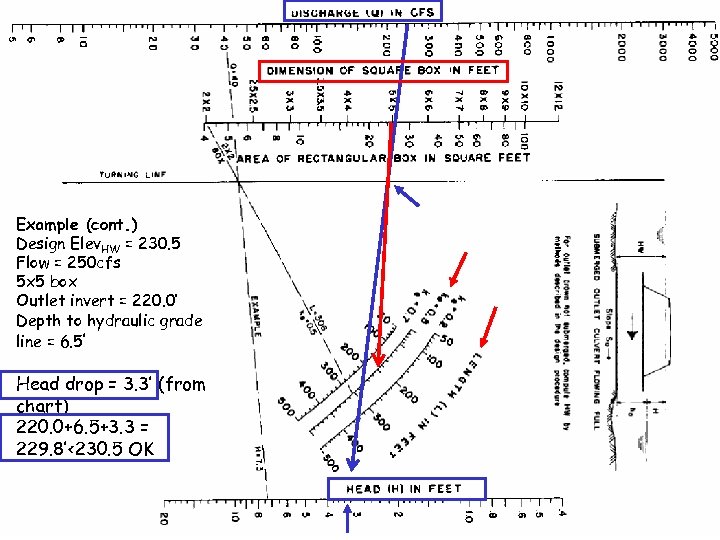Example (cont. ) Design Elev. HW = 230. 5 Flow = 250 cfs 5 x 5 box Outlet invert = 220. 0’ Depth to hydraulic grade line = 6. 5’ Head drop = 3. 3’ (from chart) 220. 0+6. 5+3. 3 = 229. 8’<230. 5 OK