Design Implementierung und Evaluierung einer virtuellen Maschine für

Design, Implementierung und Evaluierung einer virtuellen Maschine für Oz Ralf Scheidhauer PS Lab, DFKI May 18, 1999 1

Oz q Developed at DFKI since 1991 q DFKI Oz 1. 0 (1995), DFKI Oz 2. 0 (1998) q Mozart 1. 0 (1999) m 180 000 lines of C++ m 140 000 lines of Oz m 65 000 lines documentation q Since 1996 collaboration with SICS and UCL q Application strength system: multi agents (DFKI, SICS), computer-bus scheduling (Daimler), gate scheduling (Singapore), NL (SFB), comp. biology (LMU), . . . 2

Related Work q LP, CLP [Warren 77], [Jaffer Lassez 86] q Concurrency [Saraswat 93] q AKL [Janson Haridi 90, Janson 94] q FP [Appel 92] 3

Overview q Language L q Virtual machine q Implementation q Evaluation 4

The Language L q Core language of Oz q Presentation as extension of a sub language of SML m Logic variables m Threads m Synchronization m Dynamic type system q Extensions via predefined functions lvar() logic variable unify(x, y) unification spawn(f) thread creation 5

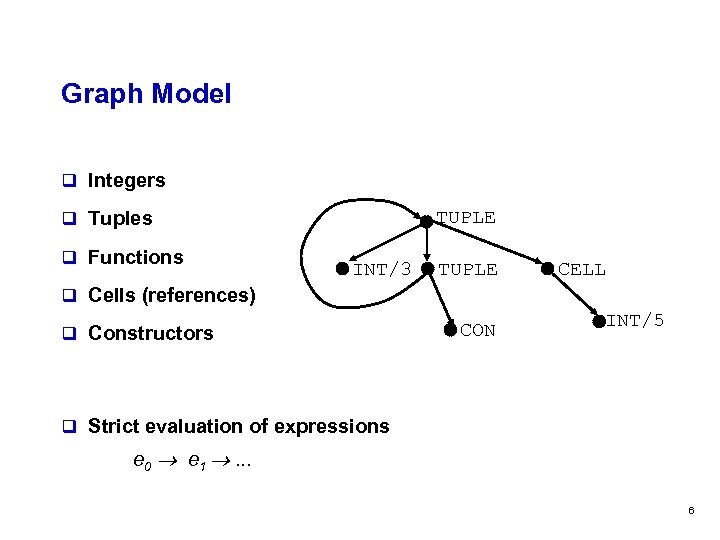Graph Model q Integers TUPLE q Tuples q Functions INT/3 TUPLE CELL q Cells (references) q Constructors CON INT/5 q Strict evaluation of expressions e 0 e 1 . . . 6

Why Logic Variables? q Programming techniques: backpatching, difference lists, . . . q Cyclic data structures q Tail recursive definition of many functions (append, map, . . . ) q Synchronization of threads q Search 7

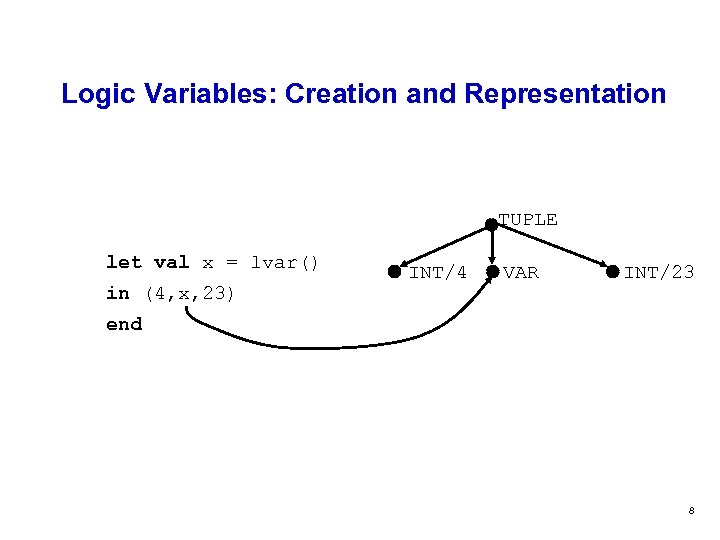Logic Variables: Creation and Representation TUPLE let val x = lvar() in (4, x, 23) INT/4 VAR INT/23 end 8

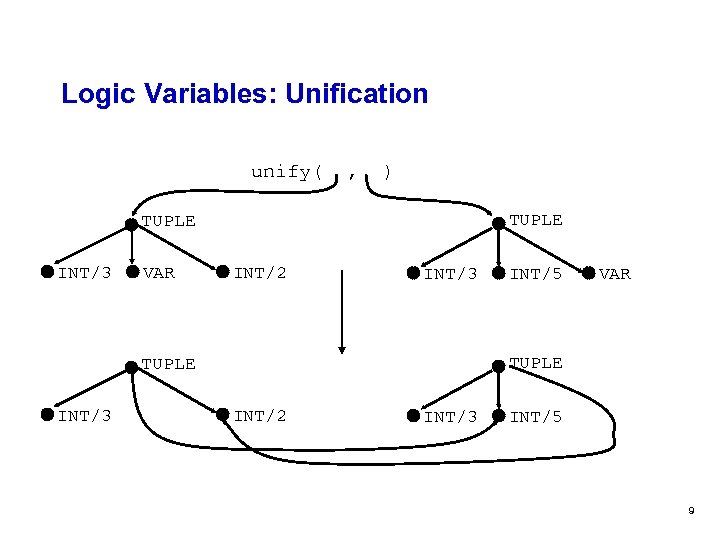Logic Variables: Unification unify( , ) TUPLE INT/3 VAR INT/2 INT/3 VAR TUPLE INT/3 INT/5 INT/2 INT/3 INT/5 9

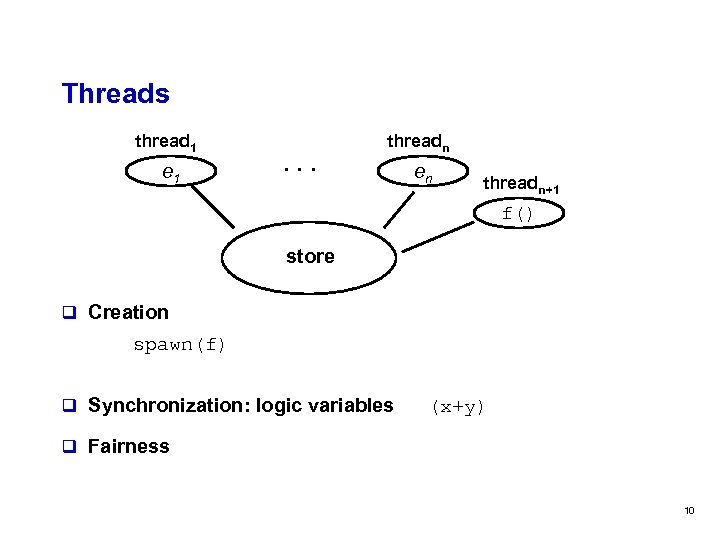Threads thread 1 e 1 . . . threadn en threadn+1 f() store q Creation spawn(f) q Synchronization: logic variables (x+y) q Fairness 10

Virtual Machine 11

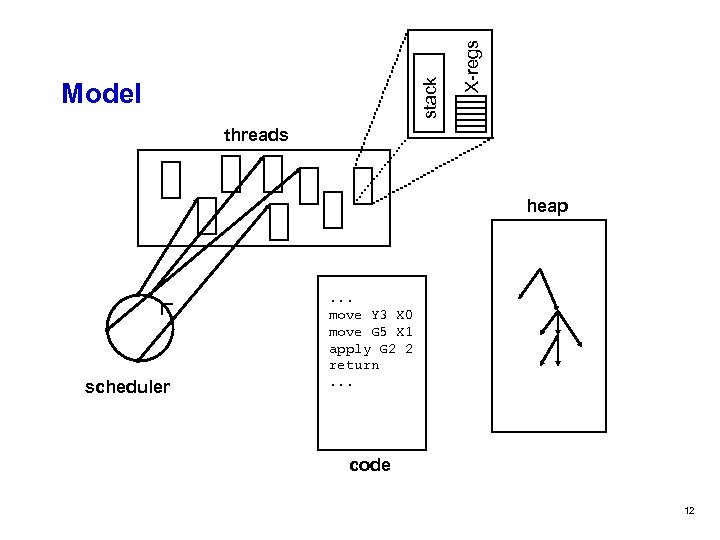X-regs stack Model threads heap scheduler . . . move Y 3 X 0 move G 5 X 1 apply G 2 2 return. . . code 12

V-Addressing q Address toplevel variables via V-registers q Loader builds data on the heap code contains direct references into heap q Example fun f(l, u) = map(fn(x)=>h(x)+g(x)+u, l) q h and g in V-register reduced memory consumption 13

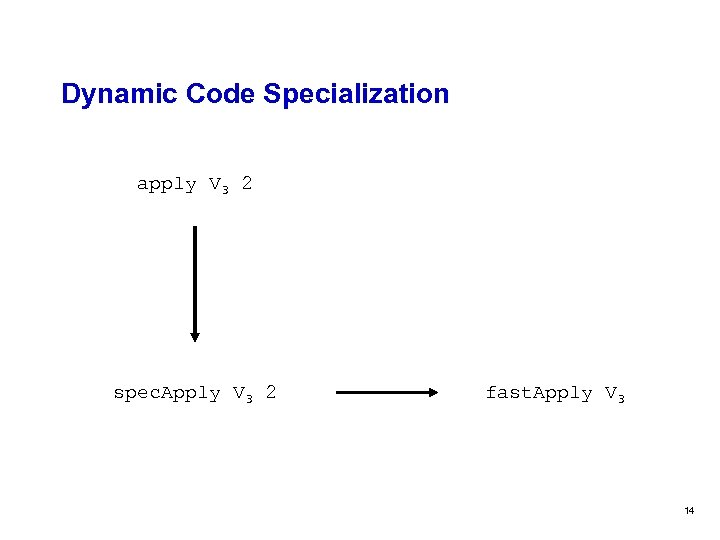Dynamic Code Specialization apply V 3 2 spec. Apply V 3 2 fast. Apply V 3 14

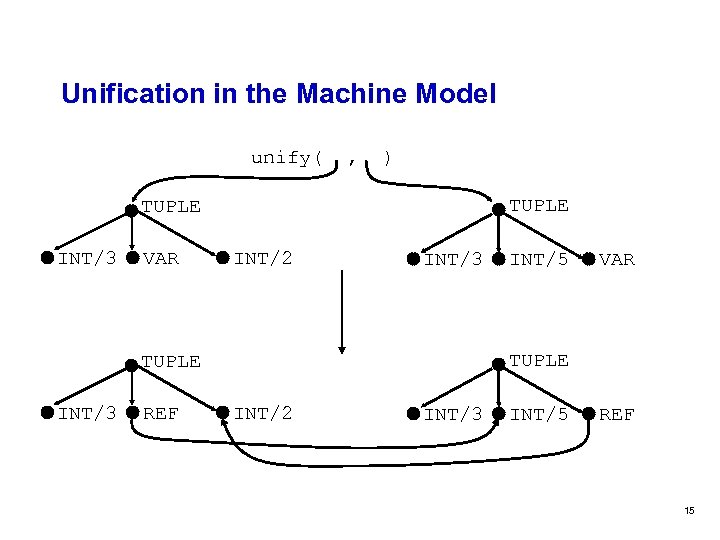Unification in the Machine Model unify( , ) TUPLE INT/3 VAR INT/2 INT/3 REF VAR TUPLE INT/3 INT/5 INT/2 INT/3 INT/5 REF 15

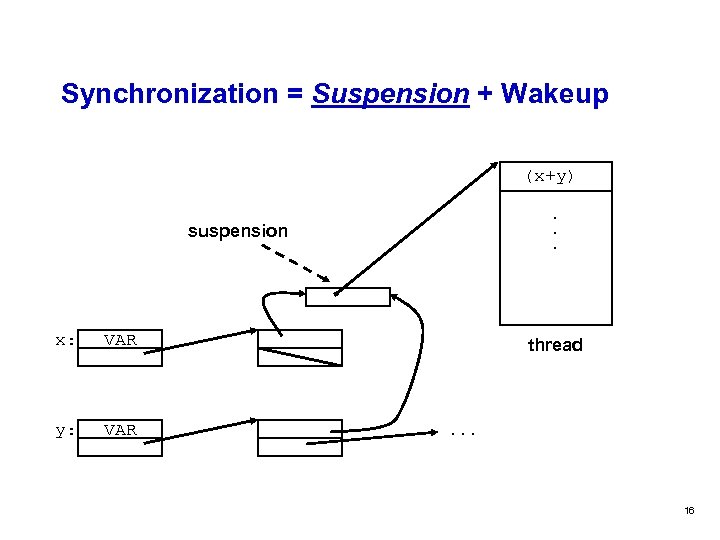Synchronization = Suspension + Wakeup (x+y). . . suspension x: VAR y: VAR thread . . . 16

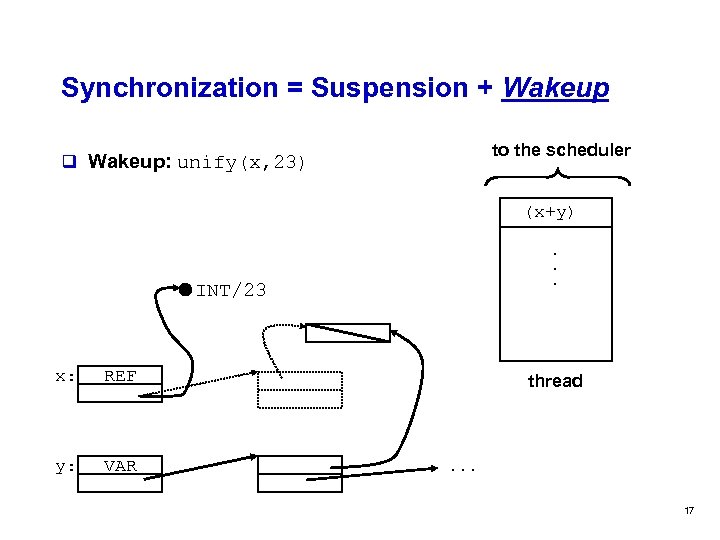Synchronization = Suspension + Wakeup to the scheduler q Wakeup: unify(x, 23) (x+y). . . INT/23 x: REF y: VAR thread . . . 17

Implementation 18

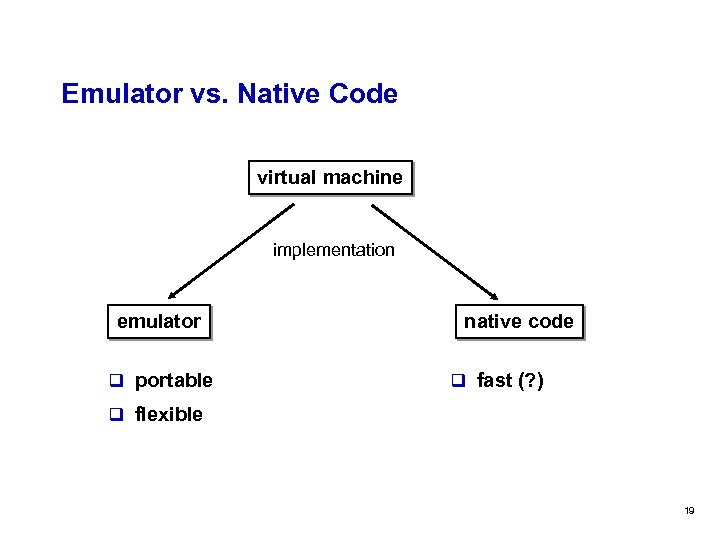Emulator vs. Native Code virtual machine implementation emulator q portable native code q fast (? ) q flexible 19

Threads q X registers: once per machine, not per thread m Save live X registers upon preemption/suspension: pessimistic guess per function m Exact determination during GC by code interpretation 20

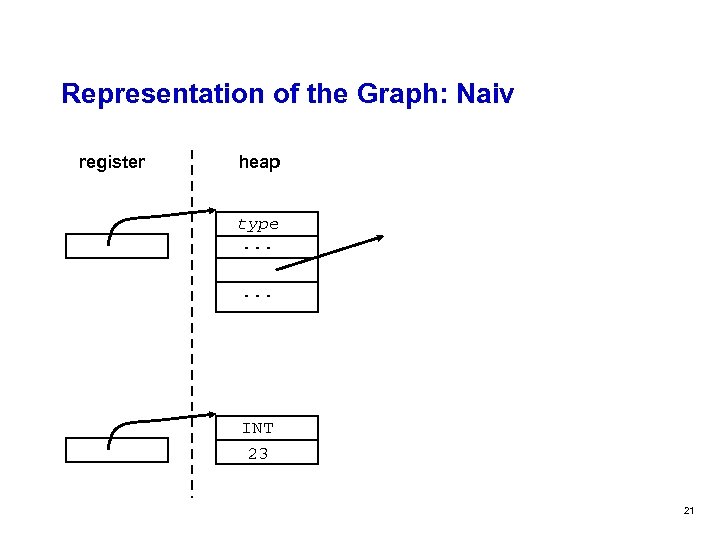Representation of the Graph: Naiv register heap type. . . INT 23 21

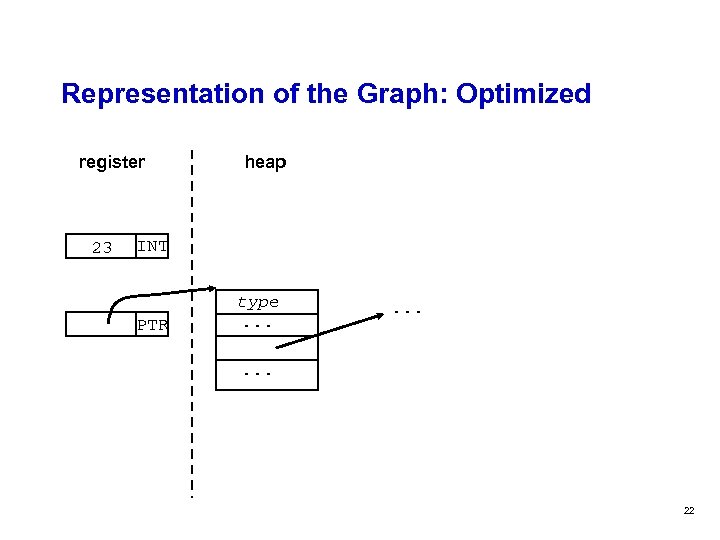Representation of the Graph: Optimized register 23 heap INT PTR type. . 22

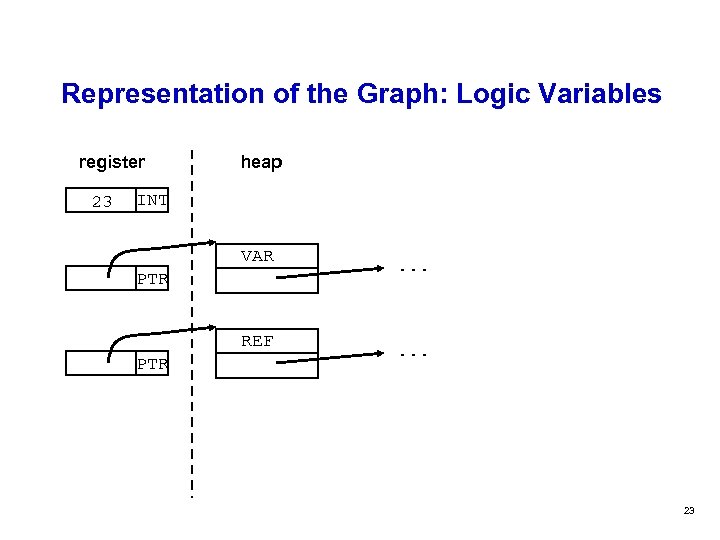Representation of the Graph: Logic Variables register 23 heap INT VAR PTR REF PTR . . . 23

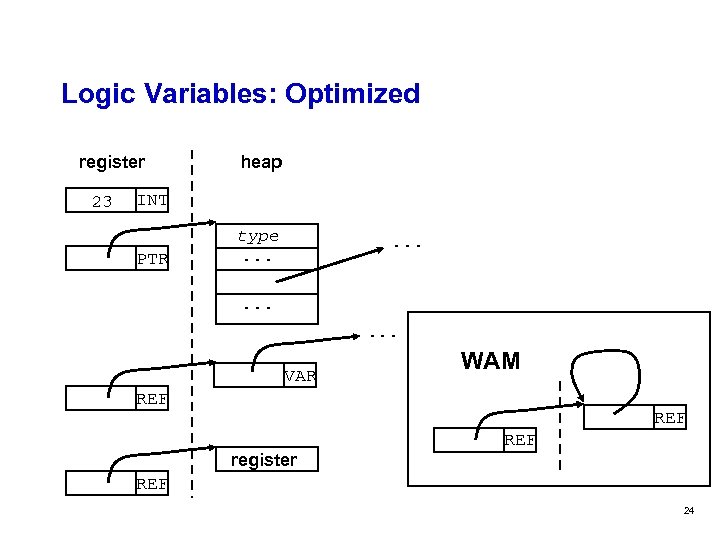Logic Variables: Optimized register 23 heap INT PTR type. . . VAR WAM REF register REF 24

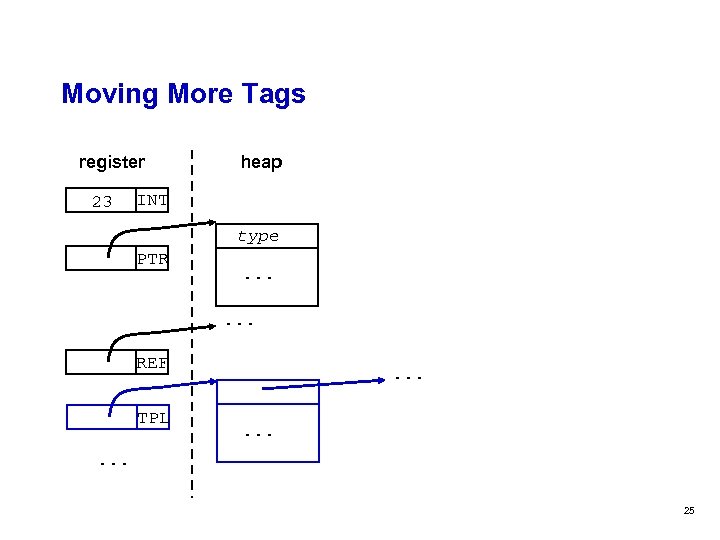Moving More Tags register 23 heap INT type PTR . . . REF TPL . . 25

Evaluation 26

Comparison with Emulators q Mozart is one of the fastest emulators q Competitive with OCAML and Java q Significantly faster than Moscow ML q Twice as fast as Sicstus Prolog and Erlang 27

Comparison with Native Code Systems q Few memory accesses (i. e. arithmetics) Mozart is easily one order of magnitude slower q Memory intensive (symbolic computation) m Difference only approx. factor 2 -3 m Mozart in single cases faster than native ML or C++ 28

Threads q Threads in Mozart are very light weight q Leading position both for creation and communication q Up to nearly 2 orders of magnitude faster than Java (creation) 29

Summary q Extended sub language of SML by logic variables and threads q Machine model m V - registers m Dynamic code specialization m Synchronization q Implementation m Efficient implementation of threads m Tagging scheme q Evaluation m Mozart is one of the fastest emulators m Compares well with native code systems on its target applications m Mozart has very light weight threads 30

Backup Slides for the Discussion 31

Logic Variables vs. Functions q Runtime fibonacci speedup takeushi 1. 18 1. 45 q Memory (large scale applications) m Use approx. 18 % of heap memory m Approx. twice as much as objects m Approx. as much as records 32

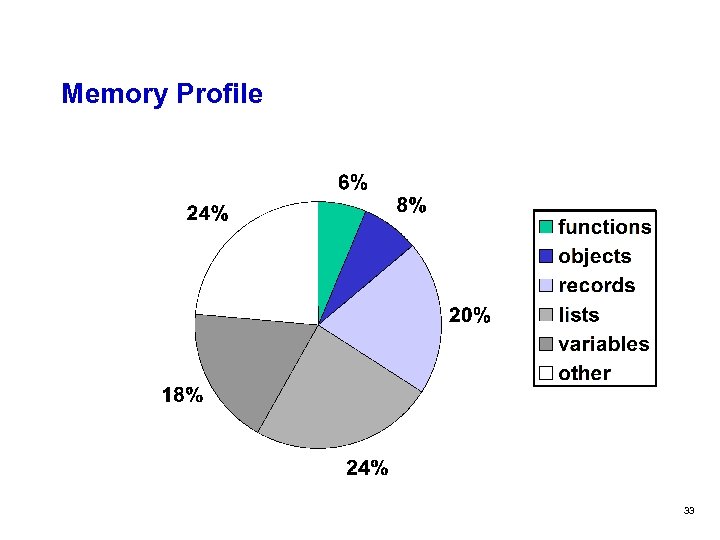Memory Profile 33

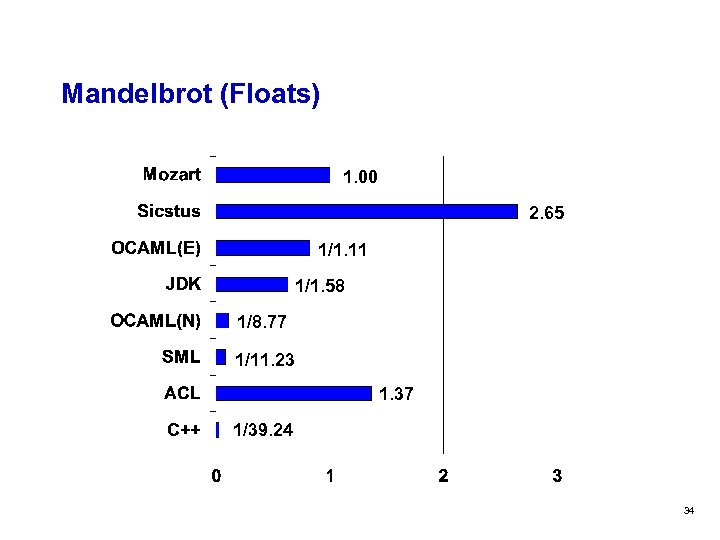Mandelbrot (Floats) 1. 00 2. 65 1/1. 11 1/1. 58 1/8. 77 1/11. 23 1. 37 1/39. 24 34

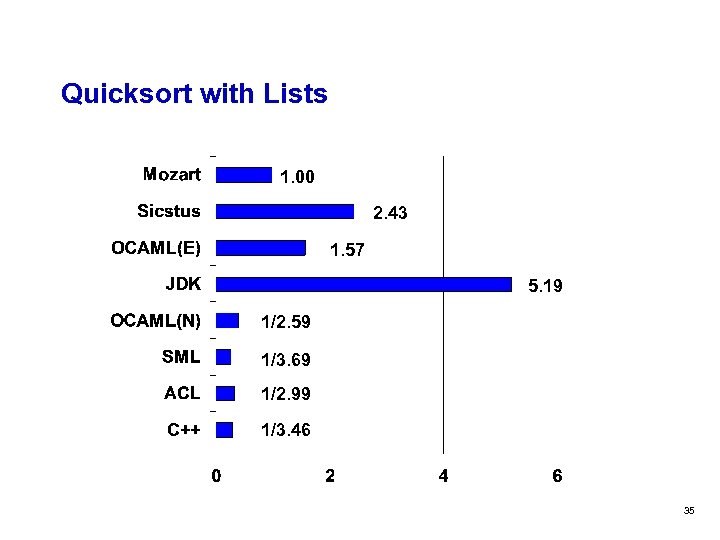Quicksort with Lists 1. 00 2. 43 1. 57 5. 19 1/2. 59 1/3. 69 1/2. 99 1/3. 46 35

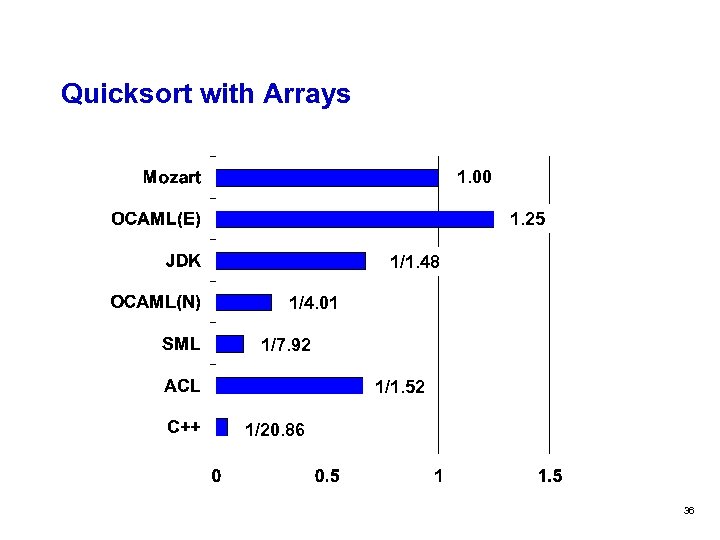Quicksort with Arrays 1. 00 1. 25 1/1. 48 1/4. 01 1/7. 92 1/1. 52 1/20. 86 36

Naiv Reverse 1. 00 1. 81 1. 59 1. 51 11. 82 1. 04 1/1. 60 2. 05 1. 70 37

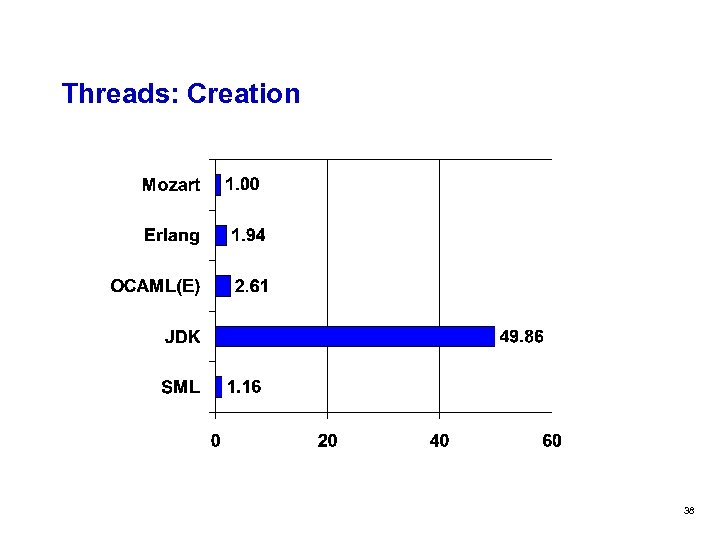Threads: Creation 38

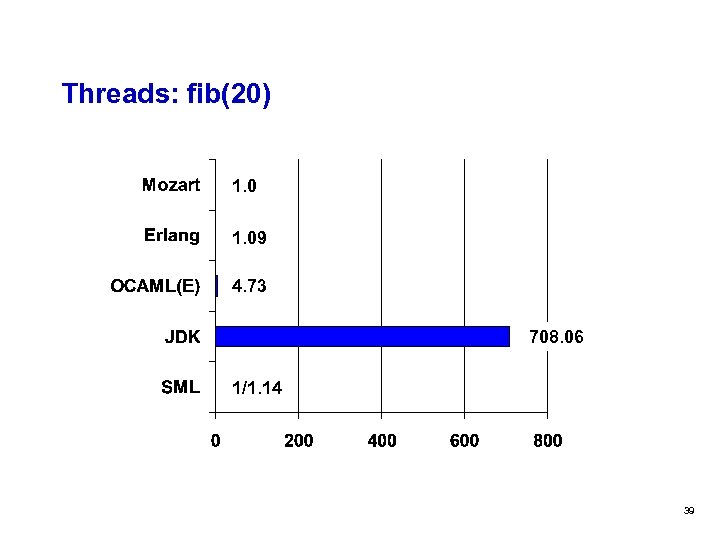Threads: fib(20) 1. 09 4. 73 708. 06 1/1. 14 39

Tagging Scheme of Mozart q 4 bit tag, but only 2 bit loss for address space (=1 GB): align structures on word boundaries q Lists, tuples: no need to unmask before type test q REF - tag m no unmask before test necessary m no unmask before deref 40

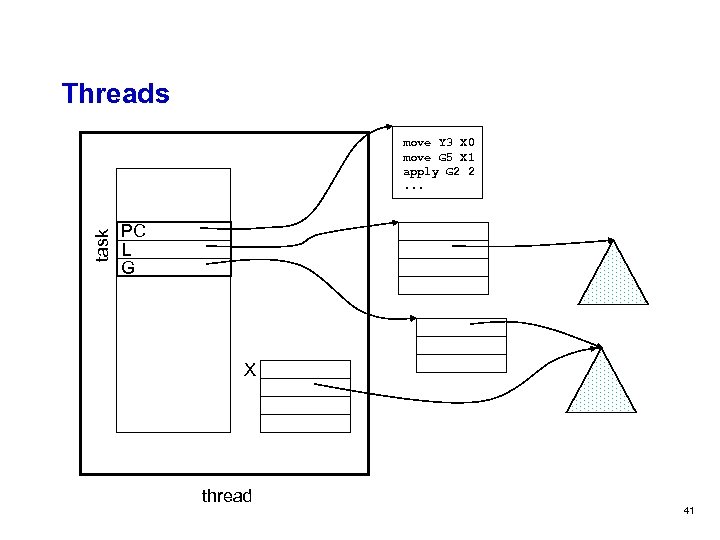Threads task move Y 3 X 0 move G 5 X 1 apply G 2 2. . . PC L G X thread 41

Emulators: Optimization Techniques q Threaded code q Instruction collapsing q Register access q Specialization q Example move Y 5 X 3 move Y 6 X 1 34 11 (SPARC) 42

Address Modes (Registers) name X thread liveness Xi notation usage temp. values, parameters local fct-body Lilocal variables global function Gi free variables virtual program Vi constants 43

Threads q Fairness: status-register PRE GC IO . . check on every function call (and return) 44

L e : : = | | | x variable n integer (e 1, . . . , en) tuple fn (x 1, . . . , xn) => e function | | e 0(e 1, . . . , en) application let val x = e in e endvariable declaration let con x in e end constructor declaration case e of p 1 => e 1 |. . . | pn=>en pattern matching Operators lvar unify spawn : () -> logic variable : -> () unification : (() -> () thread creation 45

add Xi Xk Xn Tagged Xi = X[*(PC+1)]; DEREF(Xi); if (is. Int(get. Tag(Xi))) { Tagged Xk = X[*(PC+2)]; DEREF(Xk); if (is. Int(get. Tag(Xk))) { int aux = int. Value(Xi)+int. Value(Xk); XPC(3) = oz_int(aux); ovflw+shifttag+store DISPATCH(4); } } no derefs no type tests overflow 2 2 1+2 1+1+1 3+2+2 0 (2) 0 0 2 0 (2) 3 3 -------277 (11) 23 17 6 46

Java: JIT vs. Emulator speedup quicksort (array) fib (int) fib (float) queens nrev quicksort (list) fib (thread) mandelbrot deriv (virtual) 18. 8 14. 2 4. 9 6. 1 2. 0 2. 3 1. 1 5. 4 1. 9 47