7786314f10c0101c5d4c826a16fb98c2.ppt
- Количество слайдов: 42
 Design and drawing of RC Structures CV 61 Dr. G. S. Suresh Civil Engineering Department The National Institute of Engineering Mysore-570 008 Mob: 9342188467 Email: gss_nie@yahoo. com 1
Design and drawing of RC Structures CV 61 Dr. G. S. Suresh Civil Engineering Department The National Institute of Engineering Mysore-570 008 Mob: 9342188467 Email: gss_nie@yahoo. com 1
 Portal frames 2
Portal frames 2
 Learning out Come • Introduction • Procedure for design of Portal frames • Design example 3
Learning out Come • Introduction • Procedure for design of Portal frames • Design example 3
 Books for Reference N. Krishna Raju Advanced Reinforced concrete Design Jaikrishna and O. P. Jain Plain and reinforced concrete Vol 2 B. C. Punmia Reinforced Concrete Structures Vol 2 4
Books for Reference N. Krishna Raju Advanced Reinforced concrete Design Jaikrishna and O. P. Jain Plain and reinforced concrete Vol 2 B. C. Punmia Reinforced Concrete Structures Vol 2 4
 5
5
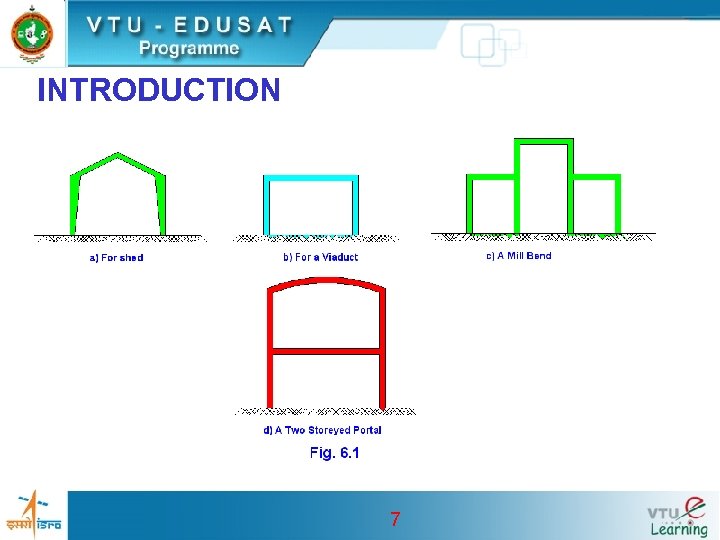
 INTRODUCTION • A portal frame consists of vertical member called Columns and top member which may be horizontal, curved or pitched. • Rigidly connected • They are used in the construction of large sheds, bridges and viaducts. • The base of portal frame may be hinged or fixed. 6
INTRODUCTION • A portal frame consists of vertical member called Columns and top member which may be horizontal, curved or pitched. • Rigidly connected • They are used in the construction of large sheds, bridges and viaducts. • The base of portal frame may be hinged or fixed. 6
 INTRODUCTION 7
INTRODUCTION 7
 For Shed 8
For Shed 8
 Inside View of Shed 9
Inside View of Shed 9
 For Rectangular Buildings 10
For Rectangular Buildings 10
 For Bridges 11
For Bridges 11
 For Viaduct 12
For Viaduct 12
 INTRODUCTION • The portal frames have high stability against lateral forces • A portal frame is a statically indeterminate structure. • In the case of buildings, the portal frames are generally spaced at intervals of 3 to 4 m • Reinforced concrete slab cast monolithically between the frames 13
INTRODUCTION • The portal frames have high stability against lateral forces • A portal frame is a statically indeterminate structure. • In the case of buildings, the portal frames are generally spaced at intervals of 3 to 4 m • Reinforced concrete slab cast monolithically between the frames 13
 INTRODUCTION Frames used for ware house sheds and workshop structures are provided with sloping of purlins and asbestos sheet roofing between the portal frames. • The base of the columns of the portal frames are either fixed or hinged. • Analysis of frames can be done by any standard methods • Columns are designed for axial force and bending moment, whereas beam is designed for bending moment and shear force • 14
INTRODUCTION Frames used for ware house sheds and workshop structures are provided with sloping of purlins and asbestos sheet roofing between the portal frames. • The base of the columns of the portal frames are either fixed or hinged. • Analysis of frames can be done by any standard methods • Columns are designed for axial force and bending moment, whereas beam is designed for bending moment and shear force • 14
 15
15
 INTRODUCTION • Step 1: Design of slabs • Step 2: Preliminary design of beams and columns • Step 3: Analysis • Step 4: Design of beams • Step 5: Design of Columns • Step 6: Design of footings 16
INTRODUCTION • Step 1: Design of slabs • Step 2: Preliminary design of beams and columns • Step 3: Analysis • Step 4: Design of beams • Step 5: Design of Columns • Step 6: Design of footings 16
 17
17
 Problem 1 • The roof of a 8 m wide hall is supported on a portal frame spaced at 4 m intervals. The height of the portal frame is 4 m. The continuous slab is 120 mm thick. Live load on roof = 1. 5 k. N/m 2, SBC of soil = 150 k. N/m 2. The columns are connected with a plinth beam and the base of the column may be assumed as fixed. Design the slab, column, beam members and suitable footing for the columns of the portal frame. Adopt M 20 grade concrete and Fe 415 steel. Also prepare the detailed structural drawing. 18
Problem 1 • The roof of a 8 m wide hall is supported on a portal frame spaced at 4 m intervals. The height of the portal frame is 4 m. The continuous slab is 120 mm thick. Live load on roof = 1. 5 k. N/m 2, SBC of soil = 150 k. N/m 2. The columns are connected with a plinth beam and the base of the column may be assumed as fixed. Design the slab, column, beam members and suitable footing for the columns of the portal frame. Adopt M 20 grade concrete and Fe 415 steel. Also prepare the detailed structural drawing. 18
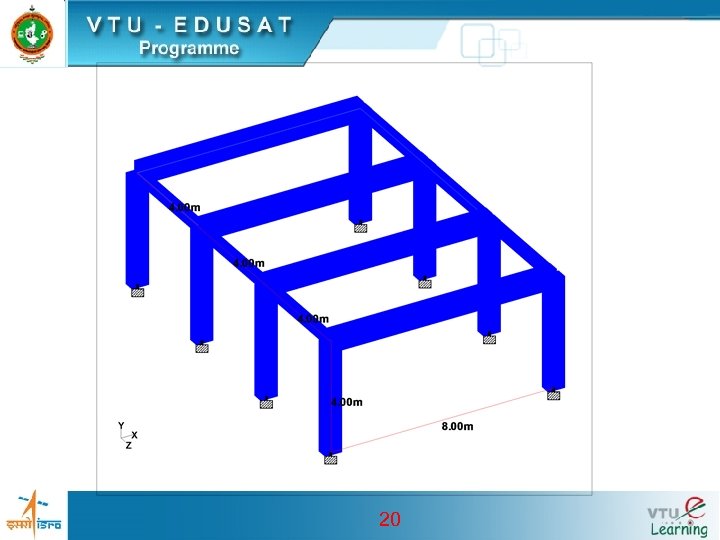
 Data given: • Spacing of frames = 4 m • Span of portal frame = 10 m • Height of columns = 4 m • Live load on roof = 1. 5 k. N/m 2 • Thickness of slab = 120 mm • Concrete: M 20 grade • Steel: Fe 415 19
Data given: • Spacing of frames = 4 m • Span of portal frame = 10 m • Height of columns = 4 m • Live load on roof = 1. 5 k. N/m 2 • Thickness of slab = 120 mm • Concrete: M 20 grade • Steel: Fe 415 19
 20
20
 21
21
 Step 1: Design of slab • Self weight of slab = 0. 12 x 24 = 2. 88 k. N/m 2 • Weight of roof finish = 0. 50 k. N/m 2 (assumed) • Ceiling finish = 0. 25 k. N/m 2 (assumed) • Total dead load wd = 3. 63 k. N/m 2 • Live load w. L = 1. 50 k. N/m 2 (Given in the data) • Maximum service load moment at interior support • Mu=1. 5 x 8. 5 = 12. 75 k. N-m/m 22
Step 1: Design of slab • Self weight of slab = 0. 12 x 24 = 2. 88 k. N/m 2 • Weight of roof finish = 0. 50 k. N/m 2 (assumed) • Ceiling finish = 0. 25 k. N/m 2 (assumed) • Total dead load wd = 3. 63 k. N/m 2 • Live load w. L = 1. 50 k. N/m 2 (Given in the data) • Maximum service load moment at interior support • Mu=1. 5 x 8. 5 = 12. 75 k. N-m/m 22
 Step 1: Design of slab (Contd) • Mulim=Qlimbd 2 (Qlim=2. 76) • = 2. 76 x 1000 x 1002 / 1 x 106 = 27. 6 k. N-m > 12. 75 k. N-m • From table 2 of SP 16 pt=0. 384; Ast=(0. 384 x 1000 x 100)/100= 384 mm 2 • Spacing of 10 mm dia bars = (78. 54 x 1000)/384= 204. 5 mm c/c • Provide #10 @ 200 c/c 23
Step 1: Design of slab (Contd) • Mulim=Qlimbd 2 (Qlim=2. 76) • = 2. 76 x 1000 x 1002 / 1 x 106 = 27. 6 k. N-m > 12. 75 k. N-m • From table 2 of SP 16 pt=0. 384; Ast=(0. 384 x 1000 x 100)/100= 384 mm 2 • Spacing of 10 mm dia bars = (78. 54 x 1000)/384= 204. 5 mm c/c • Provide #10 @ 200 c/c 23
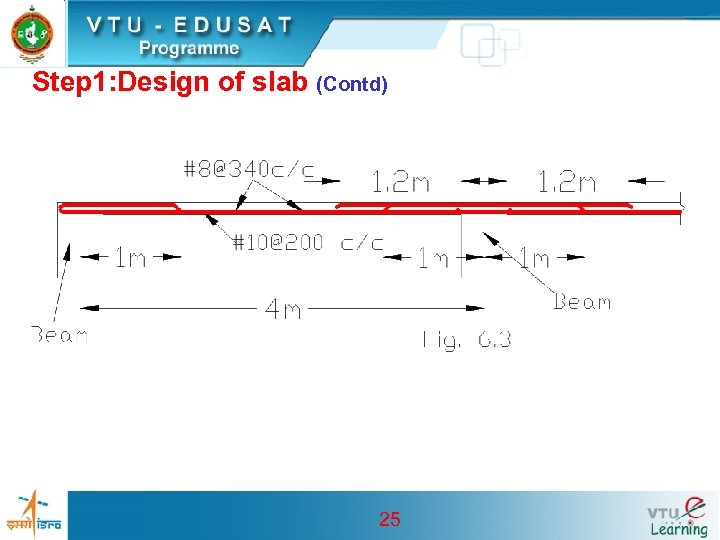
 Step 1: Design of slab (Contd) • Area of distribution steel Adist=0. 12 x 1000 x 120 / 100 = 144 mm 2 • Spacing of 8 mm dia bars = (50. 26 x 1000)/144= 349 mm c/c • Provide #8 @ 340 c/c. • Main and dist. reinforcement in the slab is shown in Fig. 6. 3 24
Step 1: Design of slab (Contd) • Area of distribution steel Adist=0. 12 x 1000 x 120 / 100 = 144 mm 2 • Spacing of 8 mm dia bars = (50. 26 x 1000)/144= 349 mm c/c • Provide #8 @ 340 c/c. • Main and dist. reinforcement in the slab is shown in Fig. 6. 3 24
 Step 1: Design of slab (Contd) 25
Step 1: Design of slab (Contd) 25
 Step 2: Preliminary design of beams and columns Beam: • Effective span = 8 m • Effective depth based on deflection criteria = 8000/12 = 666. 67 mm • Assume over all depth as 700 mm with effective depth = 650 mm, breadth b = 400 mm Column: • Let column section be equal to 400 mm x 600 mm. 26
Step 2: Preliminary design of beams and columns Beam: • Effective span = 8 m • Effective depth based on deflection criteria = 8000/12 = 666. 67 mm • Assume over all depth as 700 mm with effective depth = 650 mm, breadth b = 400 mm Column: • Let column section be equal to 400 mm x 600 mm. 26
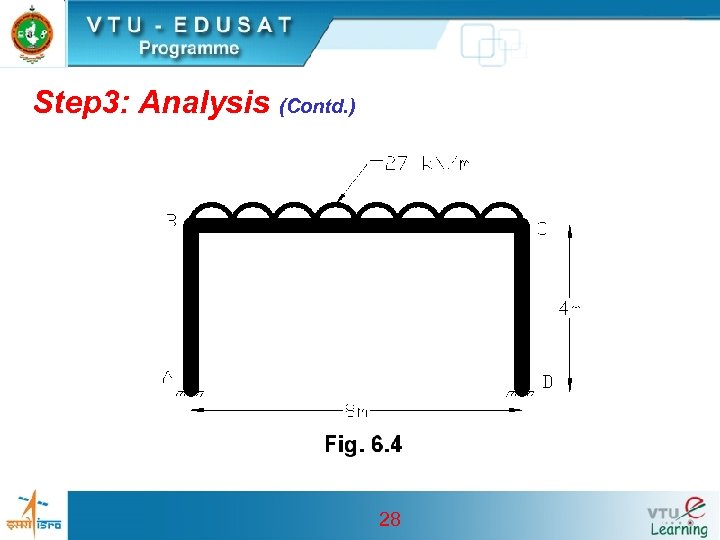
 Step 3: Analysis Load on frame i) Load from slab = (3. 63+1. 5) x 4 =20. 52 k. N/m ii) Self weight of rib of beam = 0. 4 x 0. 58 x 24 = 5. 56 k. N/m Total 27. 00 k. N/m • The portal frame subjected to the udl considered for analysis is shown in Fig. 6. 4 27
Step 3: Analysis Load on frame i) Load from slab = (3. 63+1. 5) x 4 =20. 52 k. N/m ii) Self weight of rib of beam = 0. 4 x 0. 58 x 24 = 5. 56 k. N/m Total 27. 00 k. N/m • The portal frame subjected to the udl considered for analysis is shown in Fig. 6. 4 27
 Step 3: Analysis (Contd. ) 28
Step 3: Analysis (Contd. ) 28
 Step 3: Analysis(Contd) • The moments in the portal frame fixed at the base and loaded as shown in Fig. 6. 4 are analysed by moment distribution • IAB = 400 x 6003/12 = 72 x 108 mm 4, • IBC= 400 x 7003/12 = 114. 33 x 108 mm 4 • Stiffness Factor: • KBA= IAB / LAB = 18 x 105 • KBC= IBC / LBC = 14. 3 x 105 29
Step 3: Analysis(Contd) • The moments in the portal frame fixed at the base and loaded as shown in Fig. 6. 4 are analysed by moment distribution • IAB = 400 x 6003/12 = 72 x 108 mm 4, • IBC= 400 x 7003/12 = 114. 33 x 108 mm 4 • Stiffness Factor: • KBA= IAB / LAB = 18 x 105 • KBC= IBC / LBC = 14. 3 x 105 29
 Step 3: Analysis(Contd) • Distribution Factors: • Fixed End Moments: • MFAB= MFBA= MFCD= MFDC 0 • MFBC= =-144 k. N-m • and MFCB= =144 k. N-m 30
Step 3: Analysis(Contd) • Distribution Factors: • Fixed End Moments: • MFAB= MFBA= MFCD= MFDC 0 • MFBC= =-144 k. N-m • and MFCB= =144 k. N-m 30
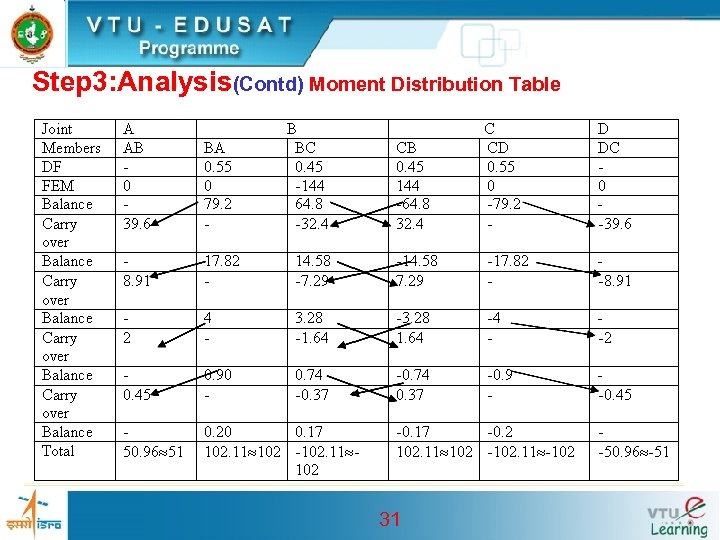 Step 3: Analysis(Contd) Moment Distribution Table 31
Step 3: Analysis(Contd) Moment Distribution Table 31
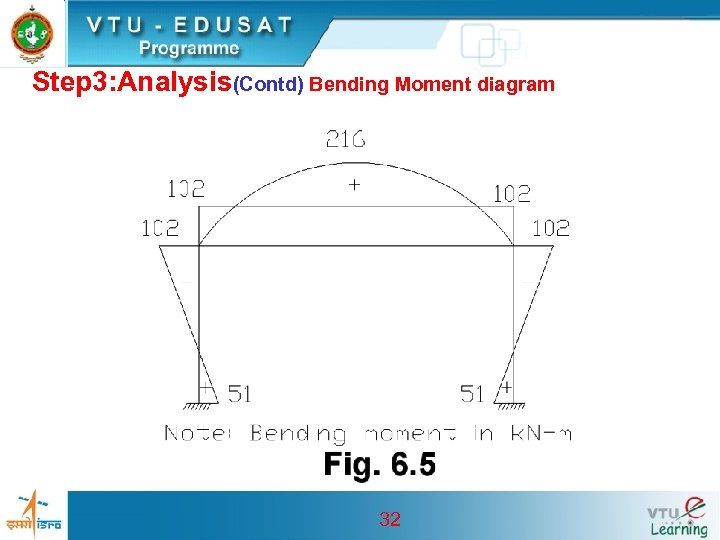 Step 3: Analysis(Contd) Bending Moment diagram 32
Step 3: Analysis(Contd) Bending Moment diagram 32
 Step 3: Analysis(Contd) Design moments: • Service load end moments: MB=102 k. N-m, MA=51 k. N-m • Design end moments Mu. B=1. 5 x 102 = 153 k. N-m, Mu. A=1. 5 x 51=76. 5 k. N-m • Service load mid span moment in beam = 27 x 82/8 – 102 =114 k. N-m • Design mid span moment Mu+ =1. 5 x 114 =171 k. N-m • Maximum Working shear force (at B or C) in beam = 0. 5 x 27 x 8 = 108 k. N • Design shear force Vu = 1. 5 x 108 = 162 k. N 33
Step 3: Analysis(Contd) Design moments: • Service load end moments: MB=102 k. N-m, MA=51 k. N-m • Design end moments Mu. B=1. 5 x 102 = 153 k. N-m, Mu. A=1. 5 x 51=76. 5 k. N-m • Service load mid span moment in beam = 27 x 82/8 – 102 =114 k. N-m • Design mid span moment Mu+ =1. 5 x 114 =171 k. N-m • Maximum Working shear force (at B or C) in beam = 0. 5 x 27 x 8 = 108 k. N • Design shear force Vu = 1. 5 x 108 = 162 k. N 33
 Step 4: Design of beams: • The beam of an intermediate portal frame is designed. The mid span section of this beam is designed as a T-beam and the beam section at the ends are designed as rectangular section. Design of T-section for Mid Span : • Design moment Mu=171 k. N-m • Flange width bf= • Here Lo=0. 7 x L = 0. 7 x 8 =5. 6 m • bf= 5. 6/6+0. 4+6 x 0. 12=2 m 34
Step 4: Design of beams: • The beam of an intermediate portal frame is designed. The mid span section of this beam is designed as a T-beam and the beam section at the ends are designed as rectangular section. Design of T-section for Mid Span : • Design moment Mu=171 k. N-m • Flange width bf= • Here Lo=0. 7 x L = 0. 7 x 8 =5. 6 m • bf= 5. 6/6+0. 4+6 x 0. 12=2 m 34
 Step 4: Design of T-beam: • bf/bw=5 and Df /d =0. 2 Referring to table 58 of SP 16, the moment resistance factor is given by KT=0. 459, • Mulim=KT bwd 2 fck = 0. 459 x 400 x 6002 x 20/1 x 106 = 1321. 92 k. N-m > Mu Safe • The reinforcement is computed using table 2 of SP 16 35
Step 4: Design of T-beam: • bf/bw=5 and Df /d =0. 2 Referring to table 58 of SP 16, the moment resistance factor is given by KT=0. 459, • Mulim=KT bwd 2 fck = 0. 459 x 400 x 6002 x 20/1 x 106 = 1321. 92 k. N-m > Mu Safe • The reinforcement is computed using table 2 of SP 16 35
 Step 4: Design of T- beam: • Mu/bd 2 = 171 x 106/(400 x 6002) 1. 2 for this pt=0. 359 • Ast=0. 359 x 400 x 600/100 = 861. 6 mm 2 • No of 20 mm dia bar = 861. 6/( x 202/4) =2. 74 • Hence 3 Nos. of #20 at bottom in the mid span 36
Step 4: Design of T- beam: • Mu/bd 2 = 171 x 106/(400 x 6002) 1. 2 for this pt=0. 359 • Ast=0. 359 x 400 x 600/100 = 861. 6 mm 2 • No of 20 mm dia bar = 861. 6/( x 202/4) =2. 74 • Hence 3 Nos. of #20 at bottom in the mid span 36
 Step 4: Design of Rectangular beam: • Design moment Mu. B=153 k. N-m • Mu. B/bd 2= 153 x 106/400 x 6002 1. 1 From table 2 of SP 16 pt=0. 327 • Ast=0. 327 x 400 x 600 / 100 = 784. 8 • No of 20 mm dia bar = 784. 8/( x 202/4) =2. 5 • Hence 3 Nos. of #20 at the top near the ends for a distance of o. 25 L = 2 m from face of the column as shown in Fig 6. 6 37
Step 4: Design of Rectangular beam: • Design moment Mu. B=153 k. N-m • Mu. B/bd 2= 153 x 106/400 x 6002 1. 1 From table 2 of SP 16 pt=0. 327 • Ast=0. 327 x 400 x 600 / 100 = 784. 8 • No of 20 mm dia bar = 784. 8/( x 202/4) =2. 5 • Hence 3 Nos. of #20 at the top near the ends for a distance of o. 25 L = 2 m from face of the column as shown in Fig 6. 6 37
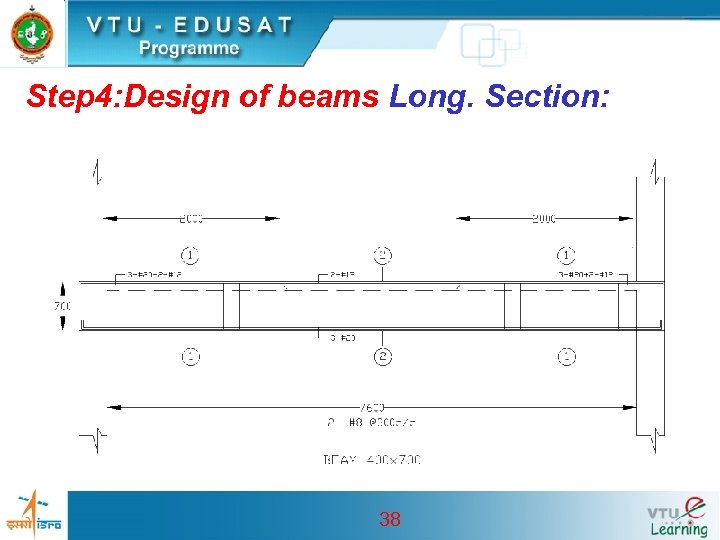 Step 4: Design of beams Long. Section: 38
Step 4: Design of beams Long. Section: 38
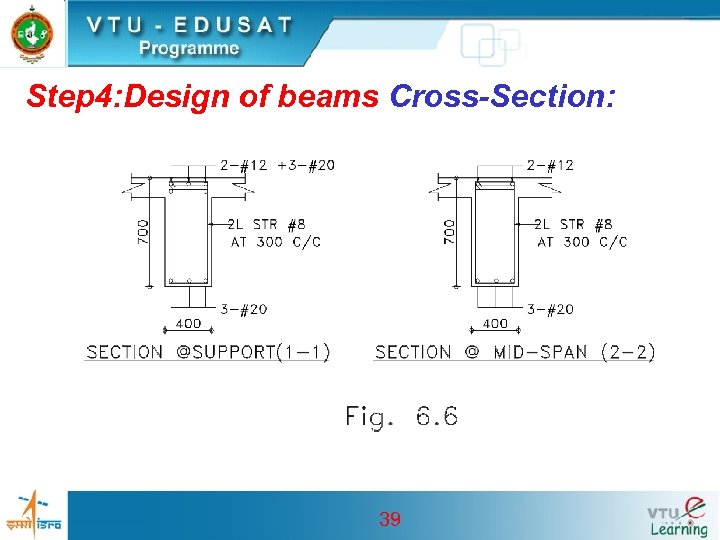 Step 4: Design of beams Cross-Section: 39
Step 4: Design of beams Cross-Section: 39
 Step 4: Check for Shear: • Nominal shear stress = pt=100 x 942/(400 x 600)=0. 39 0. 4 • Permissible stress for pt=0. 4 from table 19 c=0. 432 < v • Hence shear reinforcement is required to be designed • Strength of concrete Vuc =0. 432 x 400 x 600/1000 = 103 k. N • Shear to be carried by steel Vus=162 -103 = 59 k. N 40
Step 4: Check for Shear: • Nominal shear stress = pt=100 x 942/(400 x 600)=0. 39 0. 4 • Permissible stress for pt=0. 4 from table 19 c=0. 432 < v • Hence shear reinforcement is required to be designed • Strength of concrete Vuc =0. 432 x 400 x 600/1000 = 103 k. N • Shear to be carried by steel Vus=162 -103 = 59 k. N 40
 Step 4: Check for Shear: • Spacing 2 legged 8 mm dia stirrup sv= • Two legged #8 stirrups are provided at 300 mm c/c (equal to maximum spacing) 41
Step 4: Check for Shear: • Spacing 2 legged 8 mm dia stirrup sv= • Two legged #8 stirrups are provided at 300 mm c/c (equal to maximum spacing) 41
 Dr. G. S. Suresh Civil Engineering Department The National Institute of Engineering Mysore-570 008 Mob: 9342188467 Email: gss_nie@yahoo. com 42
Dr. G. S. Suresh Civil Engineering Department The National Institute of Engineering Mysore-570 008 Mob: 9342188467 Email: gss_nie@yahoo. com 42


