Design and Analysis Algorithm Pertemuan 11 Drs Achmad

Design and Analysis Algorithm Pertemuan 11 Drs. Achmad Ridok M. Kom Imam Cholissodin, S. Si. , M. Kom M. Ali Fauzi, S. Kom. , M. Kom. Ratih Kartika Dewi, ST, M. Kom

Contents 3 1 Decrease and Conquer 2 Insertion and Selection Sort 3 DFS and BFS 4 Binary Search Tree 2

Decrease and Conquer 1. Mengurangi permasalahan menjadi lebih kecil pada permasalahan yang sama 2. Selesaikan permasalahan yang lebih kecil tersebut 3. Kembangkan permasalahan yang lebih kecil itu sehingga menyelesaikan permasalahan sebenarnya 4. Dapat dilakukan dengan metode top down atau bottom up 3

Permasalahan eksponensial: Hitung xn § Brute Force: n-1 multiplications § Divide and Conquer: T(n) = 2*T(n/2) + 1 = n-1 § Decrease by one: T(n) = T(n-1) + 1 = n-1 T(n) = T(n/a) + a-1 § Decrease by = (a-1) = constant factor: 4 n when a = 2

Insertion sort To sort array A[0. . n-1], sort A[0. . n-2] recursively and then insert A[n-1] in its proper place among the sorted A[0. . n-2] § Usually implemented bottom up (nonrecursively) Example: Sort 6, 4, 1, 8, 5 6|4 1 8 5 4 6|1 8 5 1 4 6|8 5 1 4 6 8|5 1 4 5 6 8 Exercise : 5

Pseudo code Insertion sort 6

7

8

Kompleksitas waktu algoritma Insertion Sort: Penyelesaian: T(n) = cn + T(n – 1) = cn + { c ⋅ (n – 1) + T(n – 2) } = cn + c(n – 1) + { c ⋅ (n – 2) + T(n – 3) } = cn + c ⋅ (n – 1) + c ⋅ (n – 2) + {c(n – 3) + T(n – 4) } =. . . = cn+c⋅(n– 1)+c(n– 2)+c(n– 3)+. . . +c 2+T(1) = c{ n + (n – 1) + (n – 2) + (n – 3) +. . . + 2 } + a = c{ (n – 1)(n + 2)/2 } + a = cn 2/2+cn/2 +(a–c) = O(n 2) 9

Selection Sort § Algoritma sorting § Sorting perbandingan pada element § Terbagi menjadi 2 : § Sorted list § Sisa himpunan yang belum tersorting 10

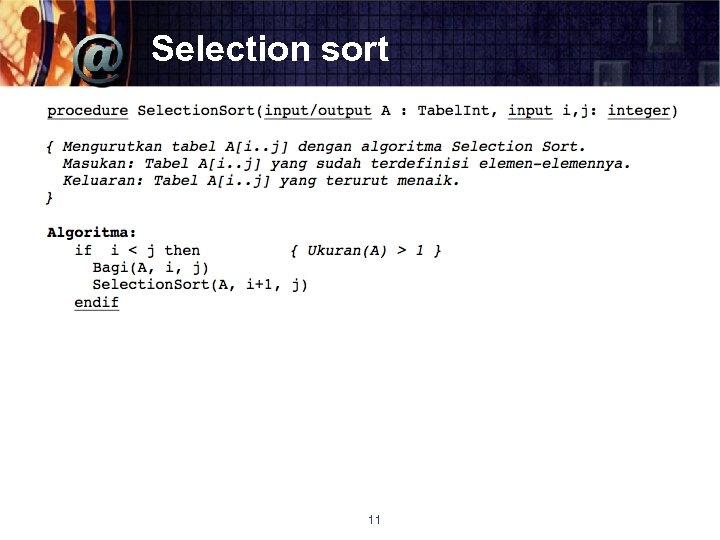Selection sort 11

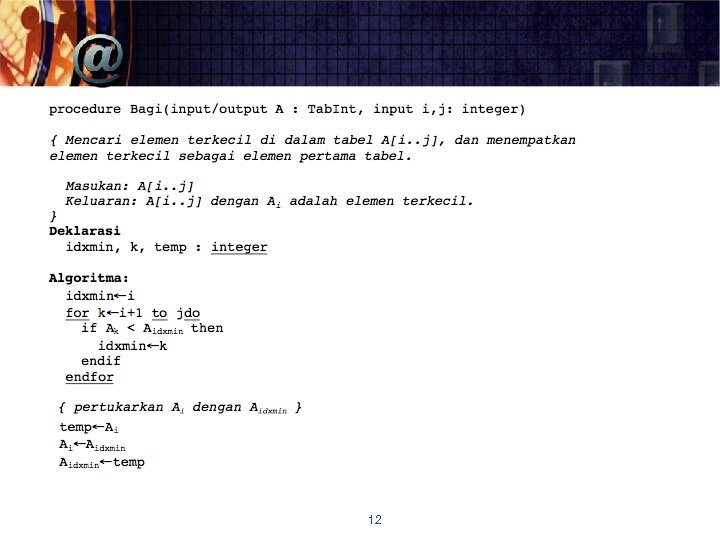12

• Misalkan tabel A berisi elemen-elemen berikut: • Langkah-langkah pengurutan dengan Selection Sort: 13

§ Kompleksitas waktu algoritma: § Penyelesaian (seperti pada Insertion Sort): 14

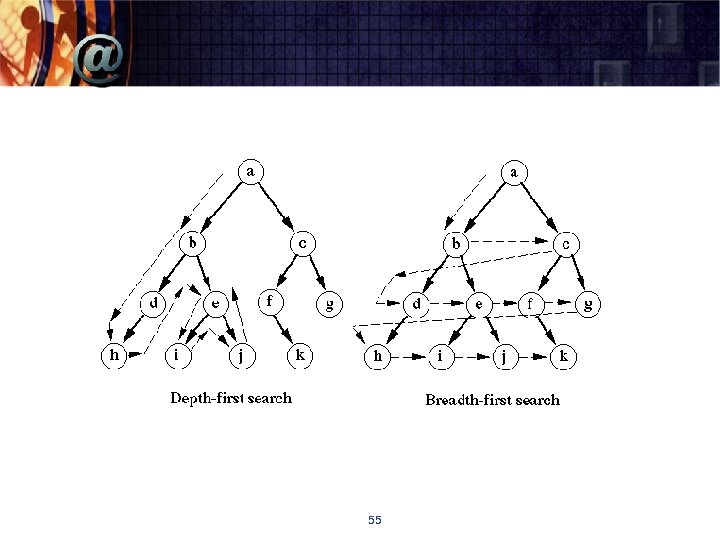
Depth-First Search (DFS) § Mengunjungi vertex-vertex pada grafik dengan selalu bergerak dari vertex yang terakhir dikunjungi ke vertex yang belum dikunjungi, lakukan backtrack apabila tidak ada vertex tetangga yang belum dikunjungi. § Rekursif atau menggunakan stack § Vertex di-push ke stack ketika dicapai untuk pertama kalinya § Sebuah vertex di-pop off atau dilepas dari stack ketika vertex tersebut merupakan vertex akhir (ketika tidak ada vertex tetangga yang belum dikunjungi) § “Redraws” atau gambar ulang grafik dalam bentuk seperti pohon (dengan edges pohon dan back edges untuk grafik tak berarah/undirected graph) 15

Pseudo code DFS 16

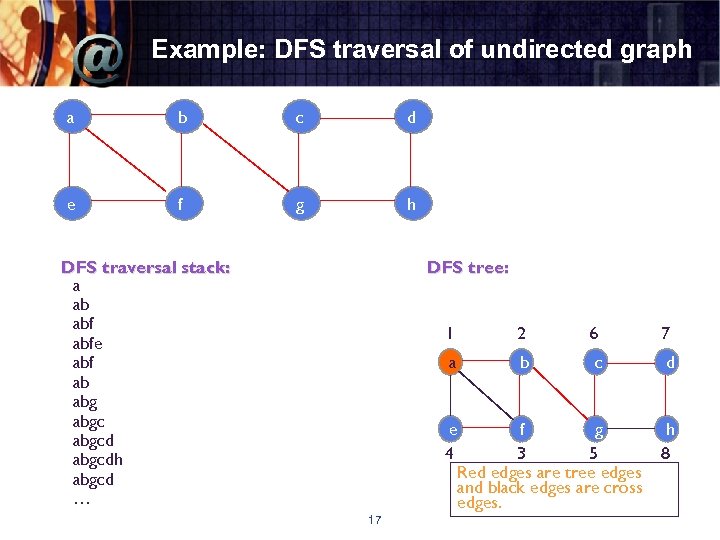Example: DFS traversal of undirected graph a b c d e f g h DFS traversal stack: a ab abfe abf ab abgcdh abgcd … DFS tree: 1 2 6 7 a b c d e f g 4 3 5 Red edges are tree edges and black edges are cross edges. 17 h 8

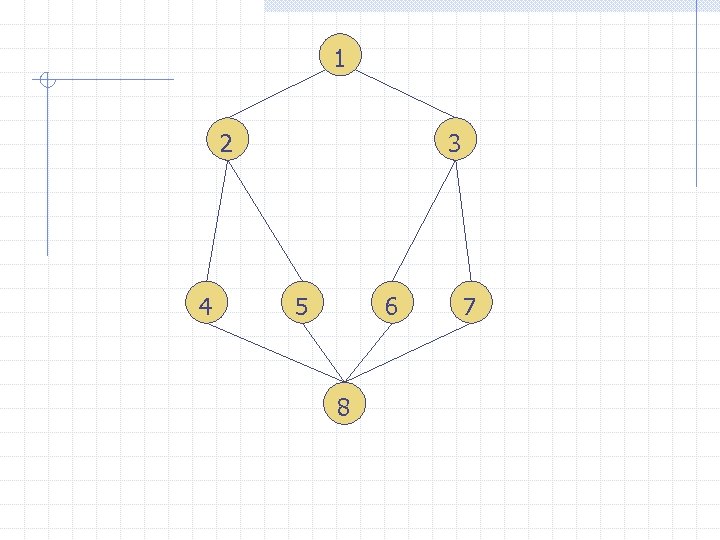1 2 4 3 5 6 8 7

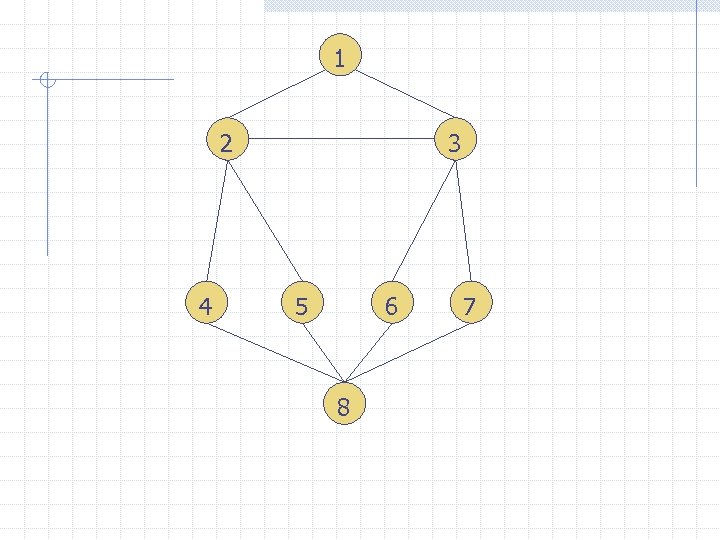1 2 4 3 5 6 8 7

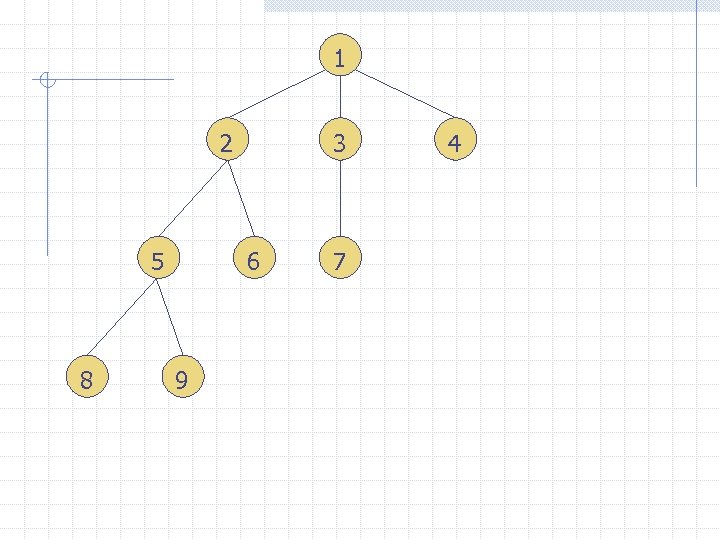1 2 5 8 3 6 9 7 4

Notes on DFS § Time complexity of DFS is O(|V|). Why? § each edge (u, v) is explored exactly once, § All steps are constant time. 21

Breadth-first search (BFS) § Mengunjungi vertex-vertex grafik dengan berpindah ke semua vertex tetangga dari vertex yang terakhir dikunjungi. § BFS menggunakan queue § Mirip dengan level ke level dari pohon merentang § “Redraws” atau gambar ulang grafik dalam bentuk seperti pohon (dengan edges pohon dan back edges untuk grafik tak berarah/undirected graph) 22

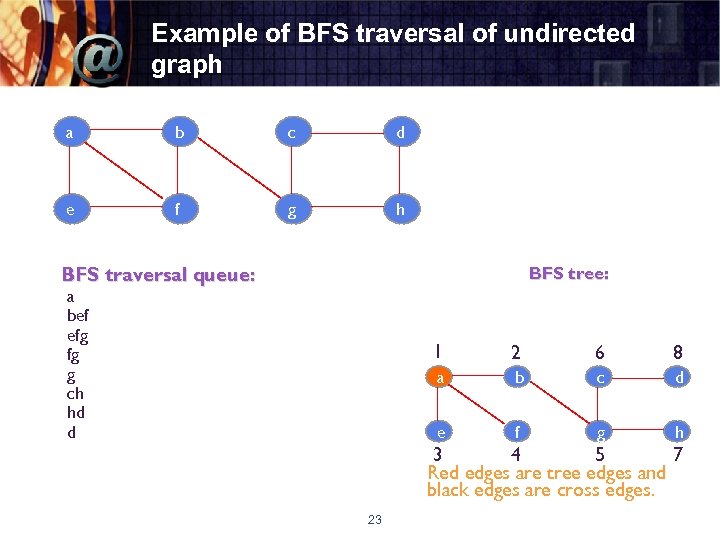Example of BFS traversal of undirected graph a b c d e f g h BFS tree: BFS traversal queue: a bef efg fg g ch hd d 1 2 6 8 a b c d e f g h 3 4 5 7 Red edges are tree edges and black edges are cross edges. 23

Pseudo code BFS 24

Notes on BFS § Asumsi: setiap simpul dapat membangkitkan b buah simpul baru. § Misalkan solusi ditemukan pada aras/level ke-d § Jumlah maksimum seluruh simpul: 1+b+b 2 +b 3 +. . . +bd =(bd+1 – 1)/(b– 1) T(n) = O(bd) Kompleksitas ruang algoritma BFS = sama dengan kompleksitas waktunya, karena semua simpul daun dari pohon harus disimpan di dalam memori selama proses pencarian. 25

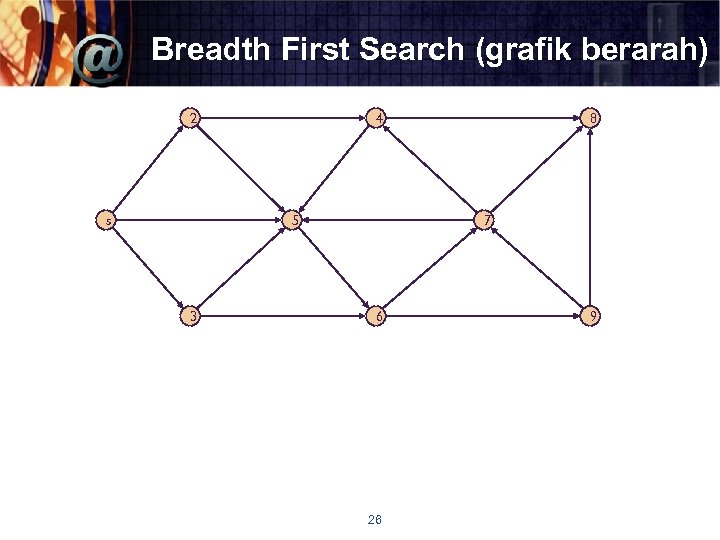Breadth First Search (grafik berarah) 2 s 4 5 3 8 7 6 26 9

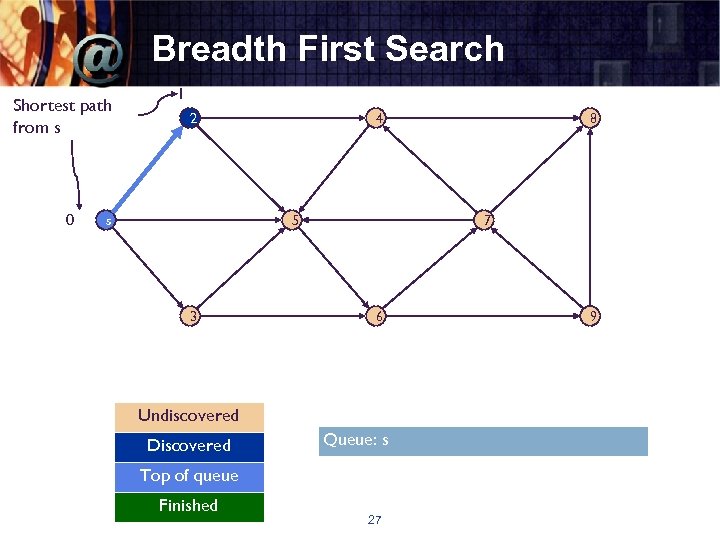Breadth First Search Shortest path from s 0 1 2 s 4 5 3 7 6 Undiscovered Discovered Queue: s Top of queue Finished 8 27 9

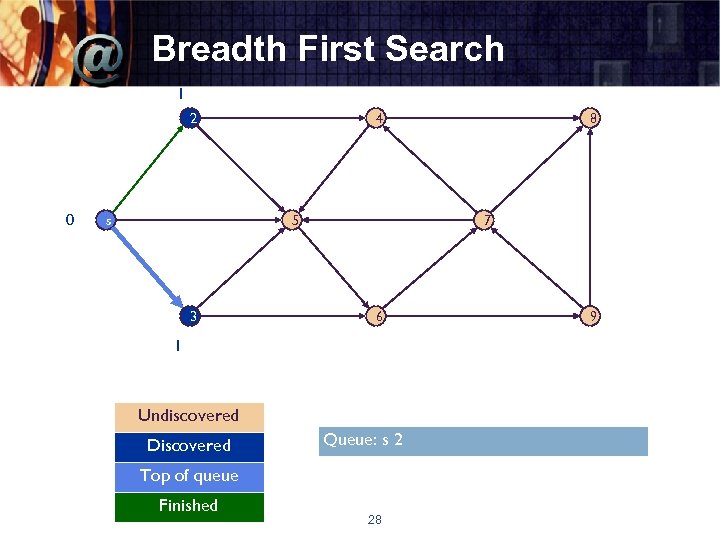Breadth First Search 1 2 0 s 4 5 3 7 6 1 Undiscovered Discovered Queue: s 2 Top of queue Finished 8 28 9

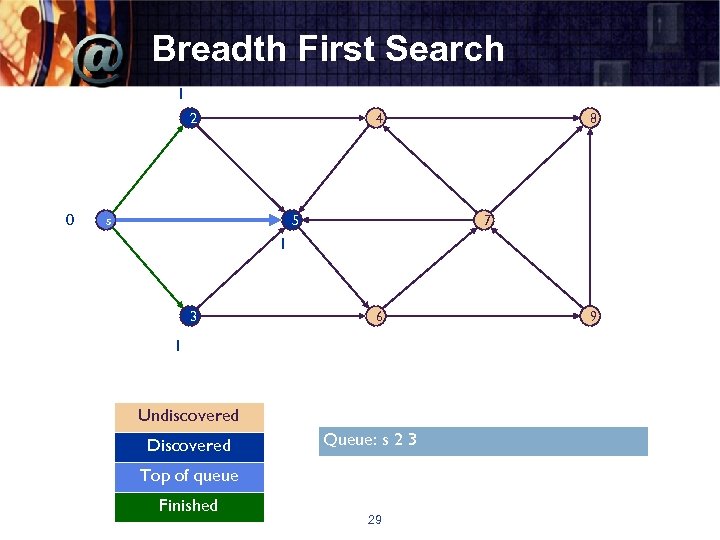Breadth First Search 1 2 0 4 5 s 8 7 1 3 6 1 Undiscovered Discovered Queue: s 2 3 Top of queue Finished 29 9

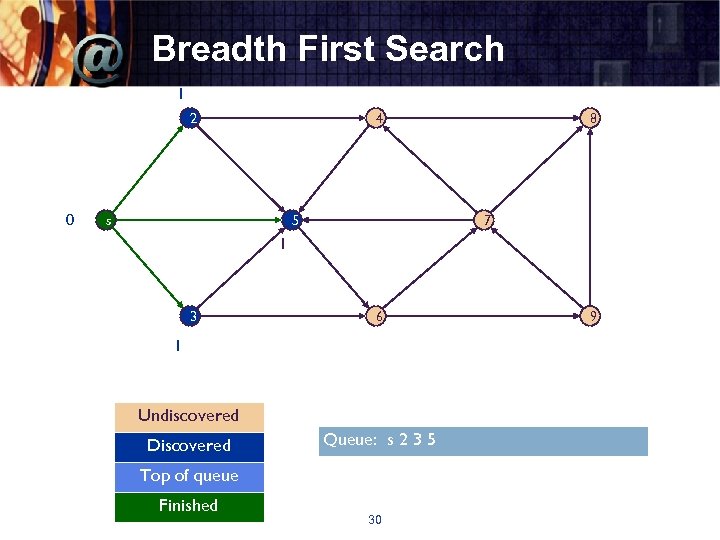Breadth First Search 1 2 0 4 s 5 8 7 1 3 6 1 Undiscovered Discovered Queue: s 2 3 5 Top of queue Finished 30 9

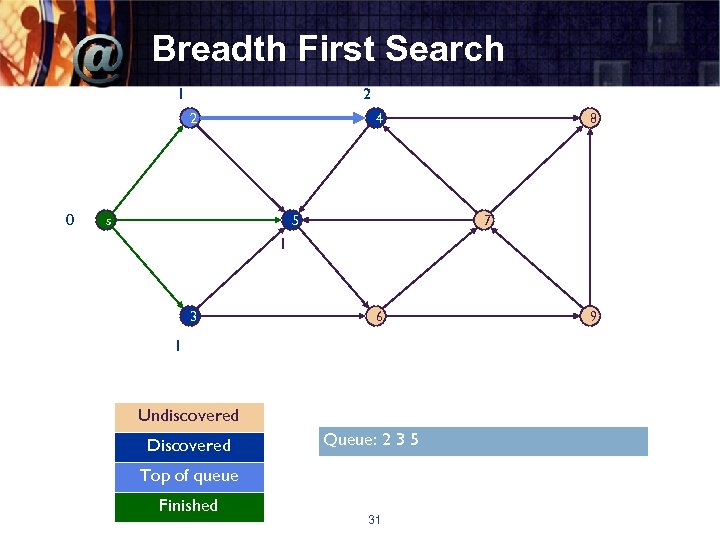Breadth First Search 1 2 2 0 4 s 5 8 7 1 3 6 1 Undiscovered Discovered Queue: 2 3 5 Top of queue Finished 31 9

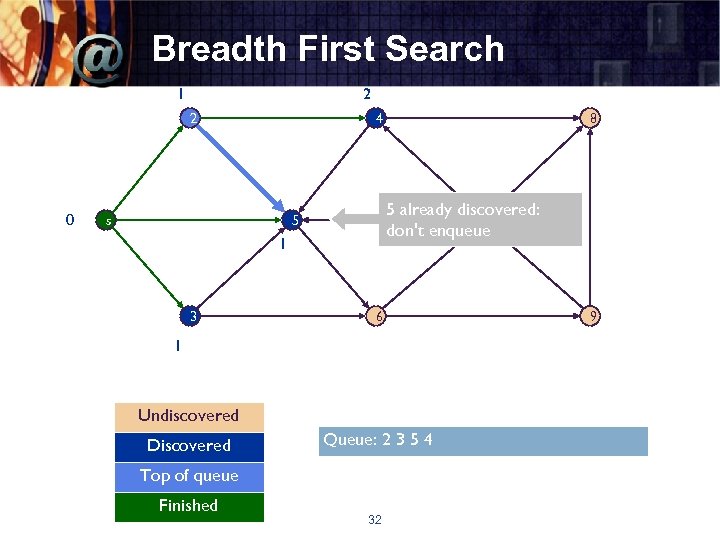Breadth First Search 1 2 2 0 4 s 5 already discovered: 7 don't enqueue 5 1 3 8 6 1 Undiscovered Discovered Queue: 2 3 5 4 Top of queue Finished 32 9

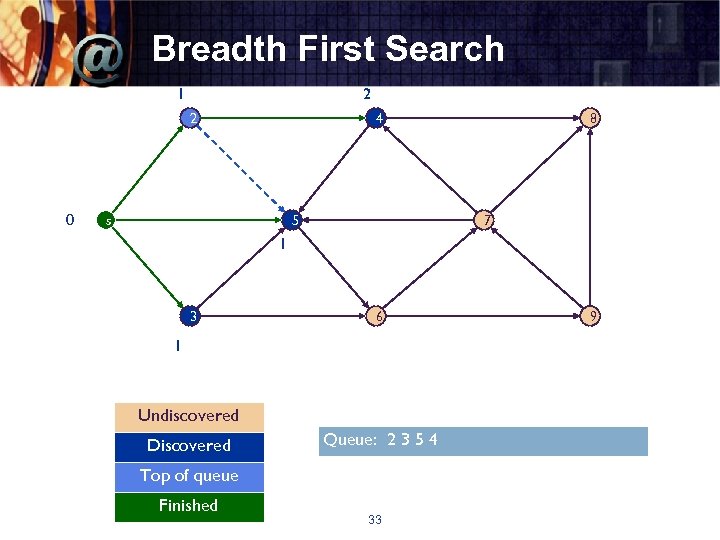Breadth First Search 1 2 2 0 4 s 5 8 7 1 3 6 1 Undiscovered Discovered Queue: 2 3 5 4 Top of queue Finished 33 9

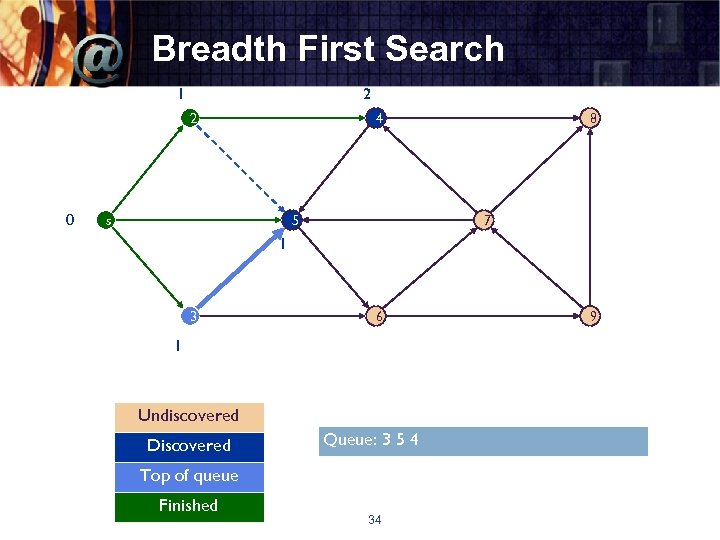Breadth First Search 1 2 2 0 4 s 5 8 7 1 3 6 1 Undiscovered Discovered Queue: 3 5 4 Top of queue Finished 34 9

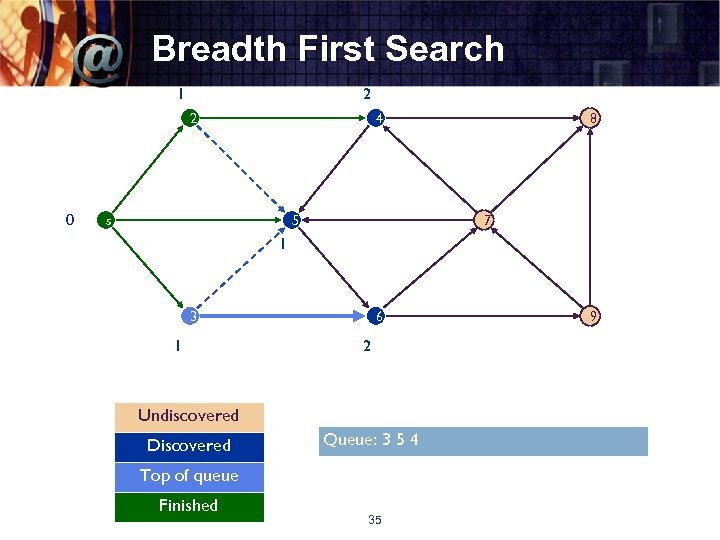Breadth First Search 1 2 2 0 4 s 5 8 7 1 6 3 1 2 Undiscovered Discovered Queue: 3 5 4 Top of queue Finished 35 9

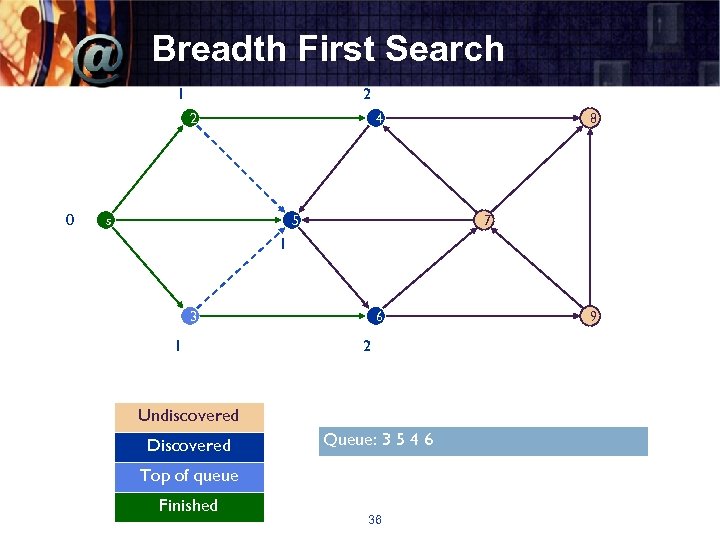Breadth First Search 1 2 2 0 4 s 5 8 7 1 3 1 6 2 Undiscovered Discovered Queue: 3 5 4 6 Top of queue Finished 36 9

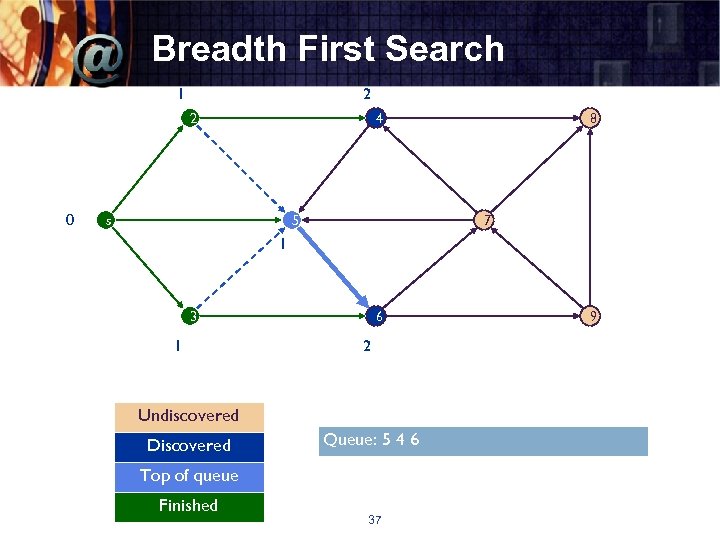Breadth First Search 1 2 2 0 4 s 5 8 7 1 3 1 6 2 Undiscovered Discovered Queue: 5 4 6 Top of queue Finished 37 9

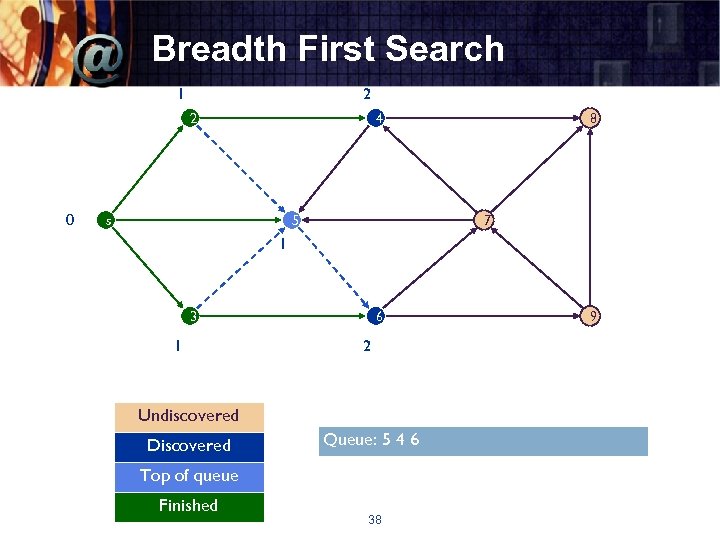Breadth First Search 1 2 2 0 4 s 5 8 7 1 3 1 6 2 Undiscovered Discovered Queue: 5 4 6 Top of queue Finished 38 9

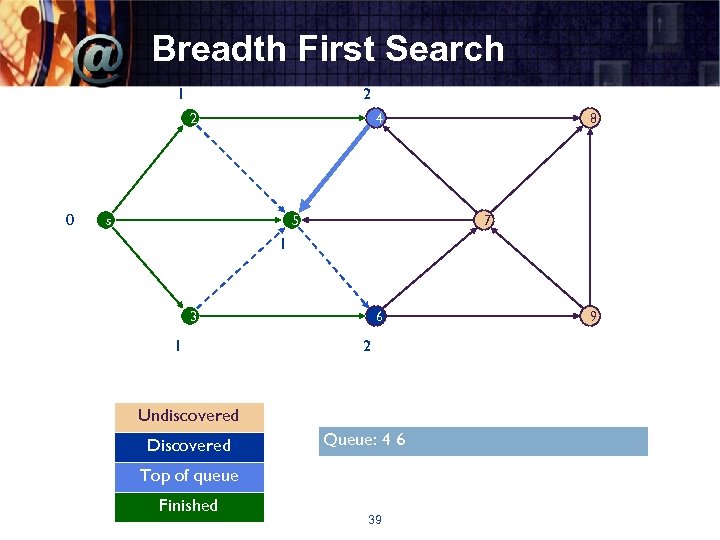Breadth First Search 1 2 2 0 4 s 5 8 7 1 3 1 6 2 Undiscovered Discovered Queue: 4 6 Top of queue Finished 39 9

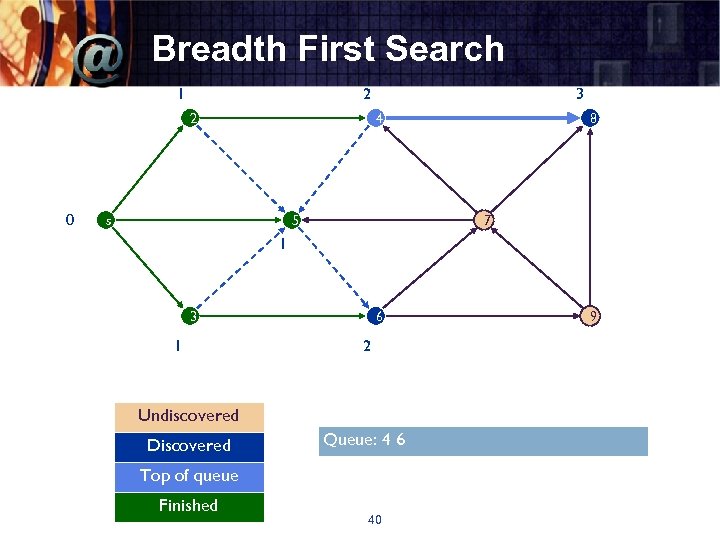Breadth First Search 1 2 2 0 3 4 s 5 8 7 1 3 1 6 2 Undiscovered Discovered Queue: 4 6 Top of queue Finished 40 9

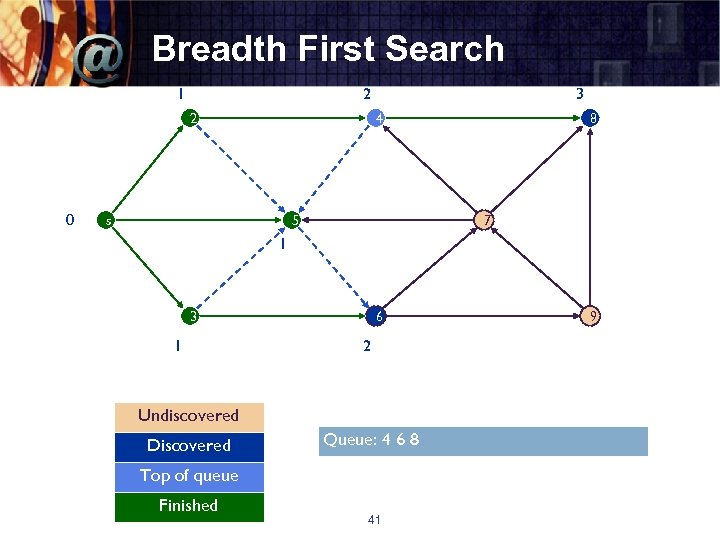Breadth First Search 1 2 2 0 3 4 s 5 8 7 1 3 1 6 2 Undiscovered Discovered Queue: 4 6 8 Top of queue Finished 41 9

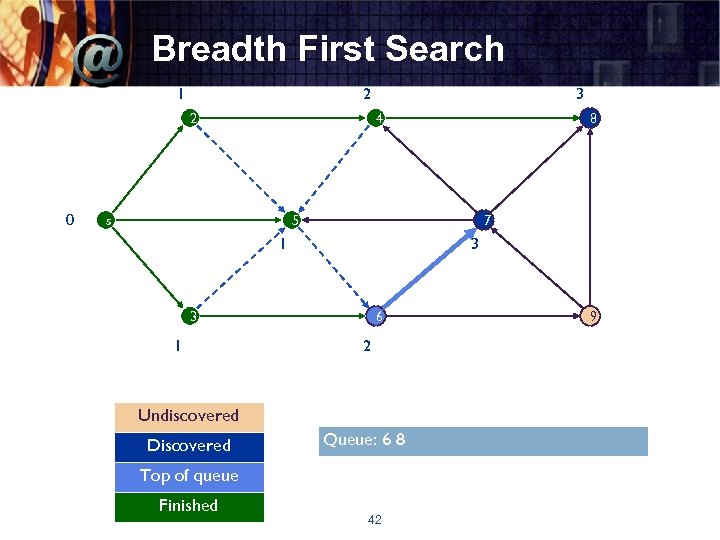Breadth First Search 1 2 2 0 3 4 s 8 7 5 1 3 3 1 6 2 Undiscovered Discovered Queue: 6 8 Top of queue Finished 42 9

Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 6 2 Undiscovered Discovered Queue: 6 8 7 Top of queue Finished 43 9 3

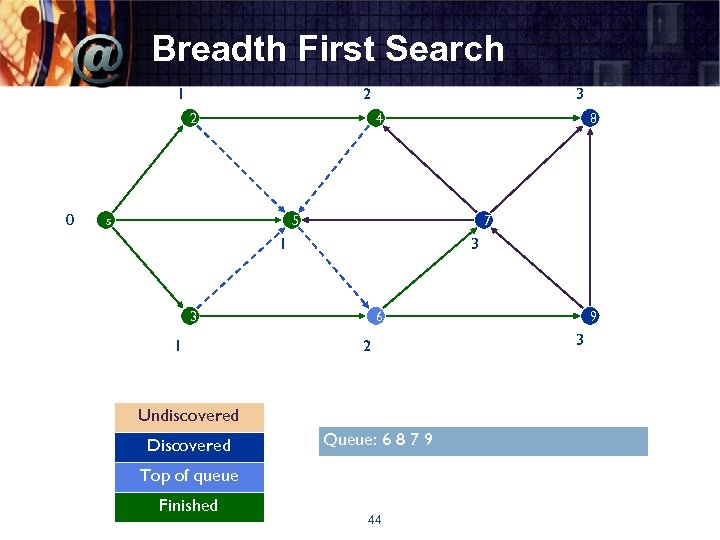Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 6 2 Undiscovered Discovered Queue: 6 8 7 9 Top of queue Finished 44 9 3

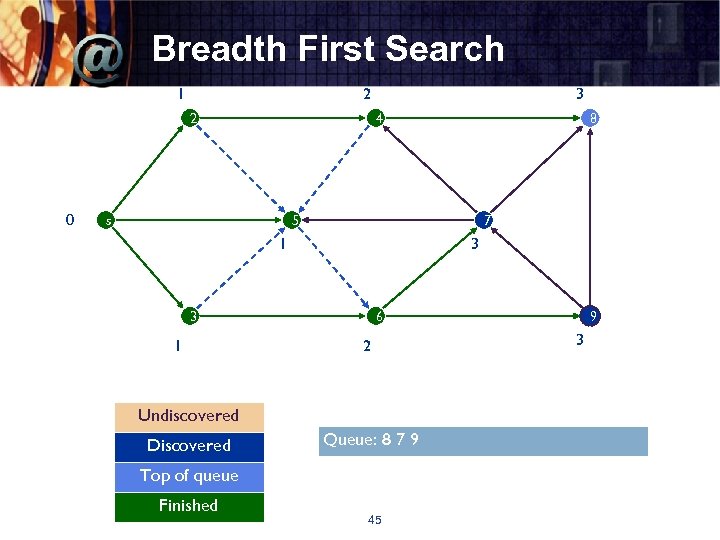Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 6 2 Undiscovered Discovered Queue: 8 7 9 Top of queue Finished 45 9 3

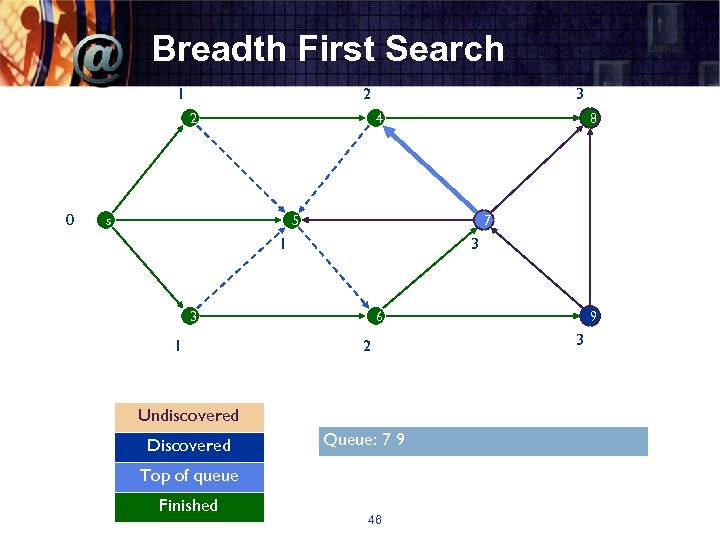Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 6 2 Undiscovered Discovered Queue: 7 9 Top of queue Finished 46 9 3

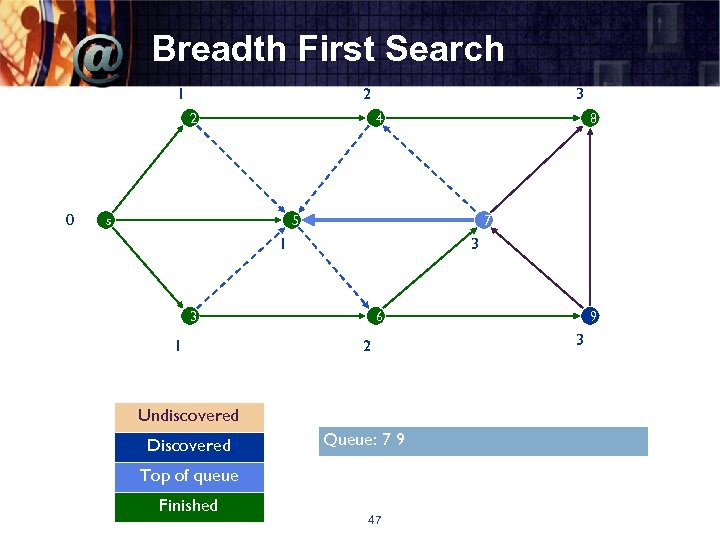Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 6 2 Undiscovered Discovered Queue: 7 9 Top of queue Finished 47 9 3

Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 6 2 Undiscovered Discovered Queue: 7 9 Top of queue Finished 48 9 3

Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 6 2 Undiscovered Discovered Queue: 7 9 Top of queue Finished 49 9 3

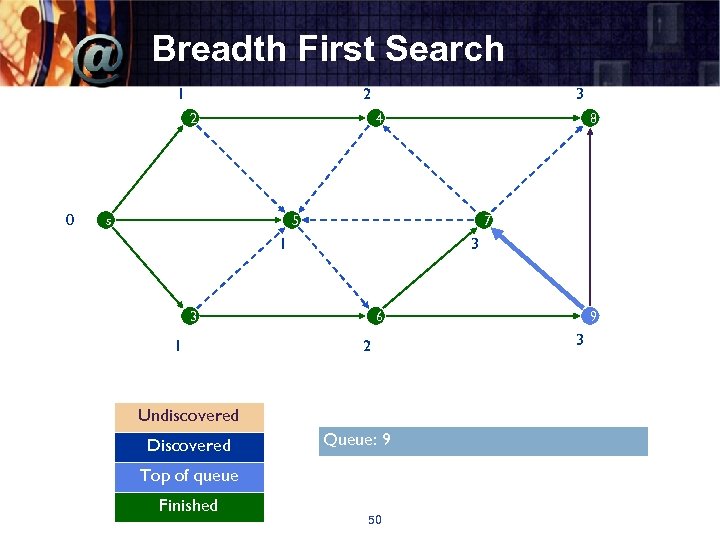Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 6 2 Undiscovered Discovered Queue: 9 Top of queue Finished 50 9 3

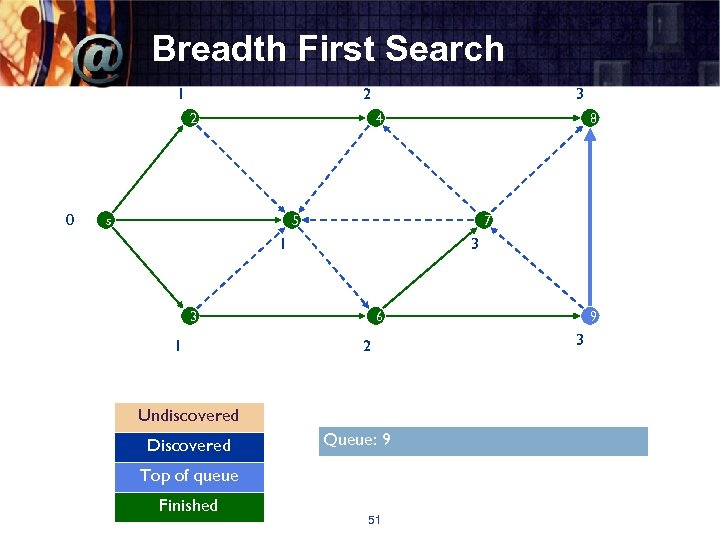Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 6 2 Undiscovered Discovered Queue: 9 Top of queue Finished 51 9 3

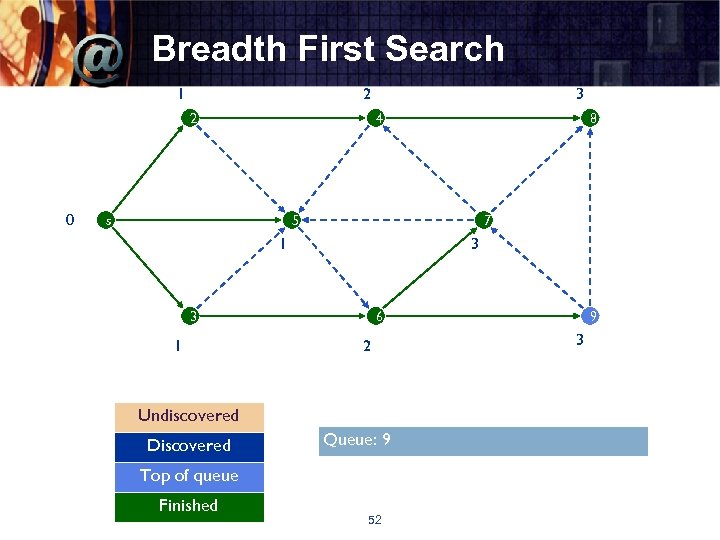Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 6 2 Undiscovered Discovered Queue: 9 Top of queue Finished 52 9 3

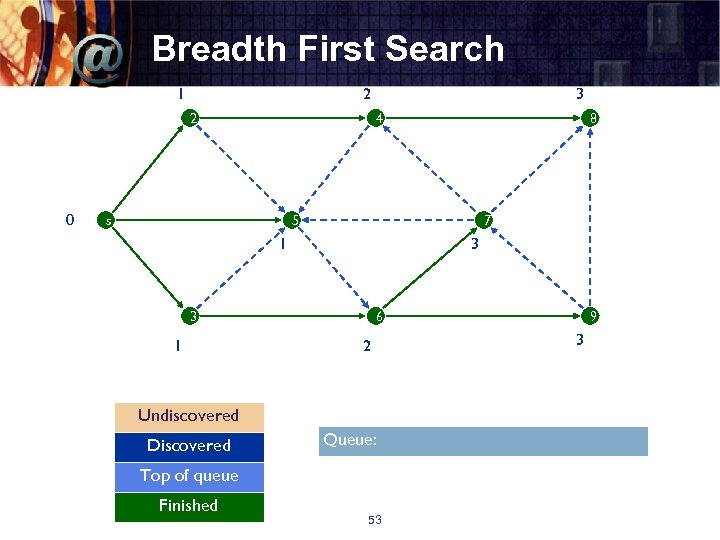Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 6 2 Undiscovered Discovered Queue: Top of queue Finished 53 9 3

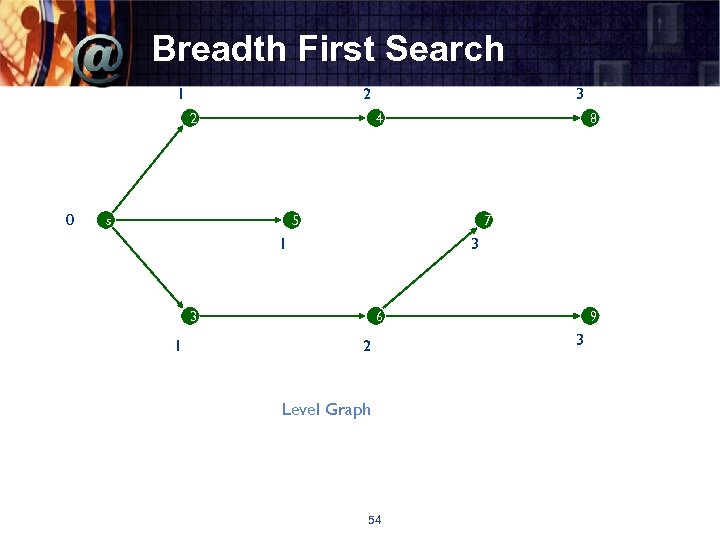Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 6 2 Level Graph 54 9 3

55

§ Latihan: Gunakan algoritma BFS dan DFS untuk menemukan pohon merentang (spanning tree) dari graf G di bawah ini jika traversalnya dimulai dari simpul k. Dalam menjawab soal ini, perlihatkan traversal BFS/DFS sebagai pohon berakar dengan e sebagai akarnya. 56

Binary Search Tree Several algorithms on BST requires recursive processing of just one of its subtrees, e. g. , k § Searching § Insertion of a new key § Finding the smallest (or the largest) key 57 k

Binary Search Tree Not a binary search tree A binary search tree 58

59

60

61

Bagaimana spider menjelajahi (surfing) web? § § Halaman web dimodelkan sebagai graf berarah Simpul menyatakan halaman web (web page) Sisi menyatakan link ke halaman web Bagaimana teknik menjelajahi web? Secara DFS atau BFS § Dimulai dari web page awal, lalu setiap link ditelusuri secara DFS sampai setiap web page tidak mengandung link. § Pada setiap halaman web, informasi di dalamnya dianalisis dan disimpan di dalam basis data index. 62

Click to edit subtitle style