6841f8c8c2caa2a0c8b6426fcb74a556.ppt
- Количество слайдов: 33

Desenvolvimento de Sistemas Baseados em Conhecimento Planejamento com Tempo, Prazos e Recursos Planejamento Hierárquico
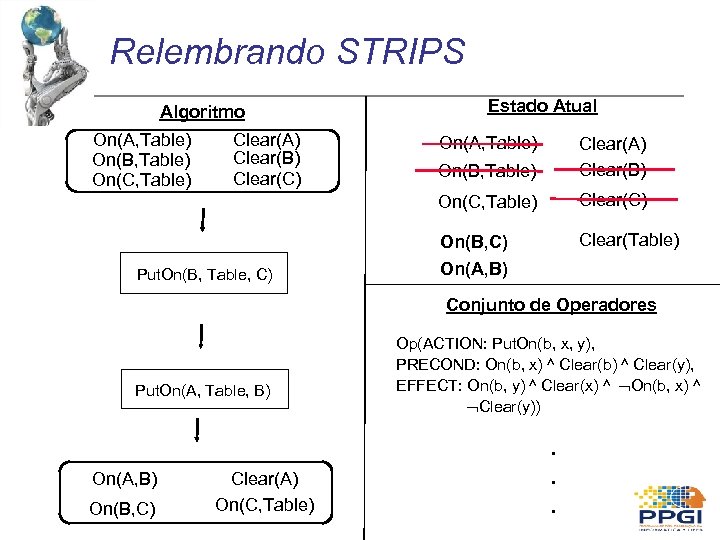
Relembrando STRIPS Algoritmo On(A, Table) On(B, Table) On(C, Table) Clear(A) Clear(B) Clear(C) Estado Atual On(A, Table) On(C, Table) Put. On(B, Table, C) On(B, Table) Clear(A) Clear(B) Clear(C) On(B, C) On(A, B) Clear(Table) Conjunto de Operadores Put. On(A, Table, B) On(A, B) On(B, C) Clear(A) On(C, Table) Op(ACTION: Put. On(b, x, y), PRECOND: On(b, x) ^ Clear(b) ^ Clear(y), EFFECT: On(b, y) ^ Clear(x) ^ On(b, x) ^ Clear(y)) . . .
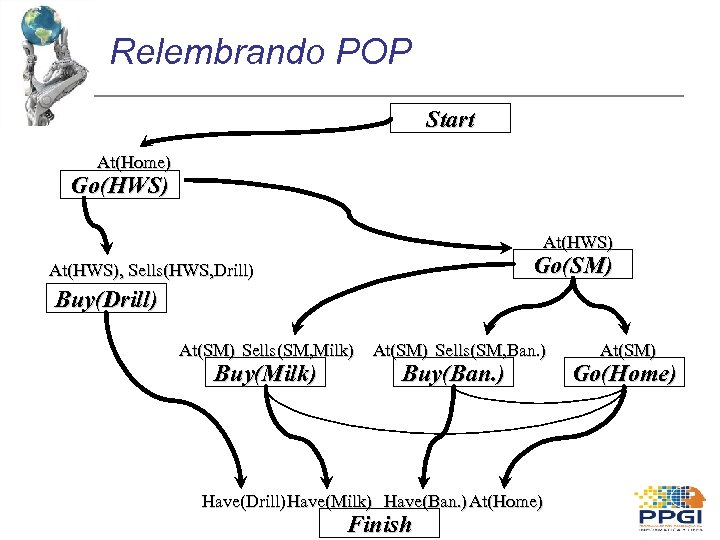
Relembrando POP Start At(Home) Go(HWS) At(HWS) Go(SM) At(HWS), Sells(HWS, Drill) Buy(Drill) At(SM) Sells(SM, Milk) At(SM) Sells(SM, Ban. ) Buy(Milk) Buy(Ban. ) Have(Drill) Have(Milk) Have(Ban. ) At(Home) Finish At(SM) Go(Home)
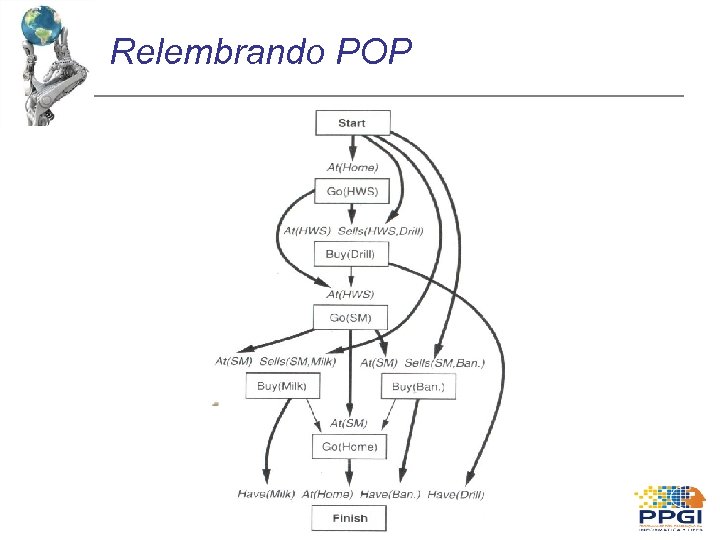
Relembrando POP

Limitações POP-STRIPS • O tempo não é levado em conta – Diz “o que”, mas não “quando” nem “por quanto tempo” – “O modelo de planejamento temporal deve ser baseado numa abordagem de intervalo explicito, o qual permita a representação de referências temporais quantitativas e qualitativas, assim como relações entre eles”. a I Ii If Duração = If - Ii

Limitações POP-STRIPS • A limitação dos recursos não é considerada – Não custa nada agir (ex: orçamento, pessoas) » Os recursos de uma brigada de incêndio, assim como a própria brigada, são limitados – Plano de viagem X orçamento

Limitações POP-STRIPS • Pré-condições e efeitos são muito limitados – Os operadores são essencialmente proposicionais » ex: sem quantificador universal nos efeitos, não se pode dizer que os componentes de uma esquadrilha atacam juntos Identified(target), available(esq) Attack(target) p Plane(p) p esq Attack(p, target)
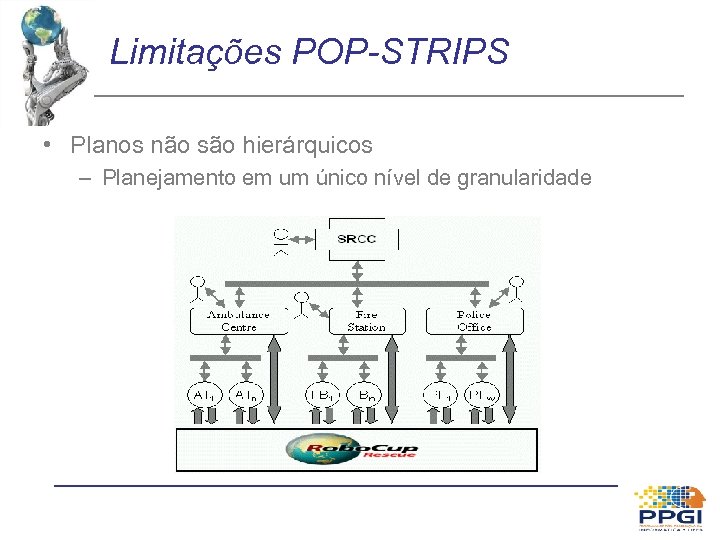
Limitações POP-STRIPS • Planos não são hierárquicos – Planejamento em um único nível de granularidade

Limitações POP-STRIPS -Operadores de baixo nível: - Mover - Girar - Zoom câmera - Identificar cadáveres

Tempo e Prazos • Job Shop Scheduling – – Completar conjunto de tarefas (jobs) Cada tarefa é composto por uma seqüência de ações Cada ação tem uma duração e pode precisar de recursos Encontrar o escalonamento mais rápido para a execução das tarefas, respeitando restrições de recursos • Exemplo de Job Shop Problem – 2 tarefas (jobs): montar dois carros C 1 e C 2 – Ações: colocar motor, colocar rodas, inspecionar – Ordem: motor antes das rodas e inspecionar no final • Como lidar com isto?

Tempo e Prazos • Acrescentar Duration(d) para ações em STRIPS • Exemplo. . . – Init (Car(C 1) Car(C 2) Engine(E 1, C 1, 30) Engine(E 2, C 2, 60) Wheels(W 1, C 1, 30) Wheels(W 2, C 2, 15)) – Goal (Done(C 1) Done(C 2)) – Action (Add. Engine(e, c), Precond: Engine (e, c, d) Car(c) Engine. In(c), Effect: Engine. In(c) Duration(d)) – Action (Add. Wheels(w, c), Precond: Wheels(w, c, d) Car(c) Effect: Wheels. On(c) Duration(d)) – Action (Inspect(c), Precond: Engine. In(c) Wheels. On(c) Car(c) Effect: Done(c) Duration(10))
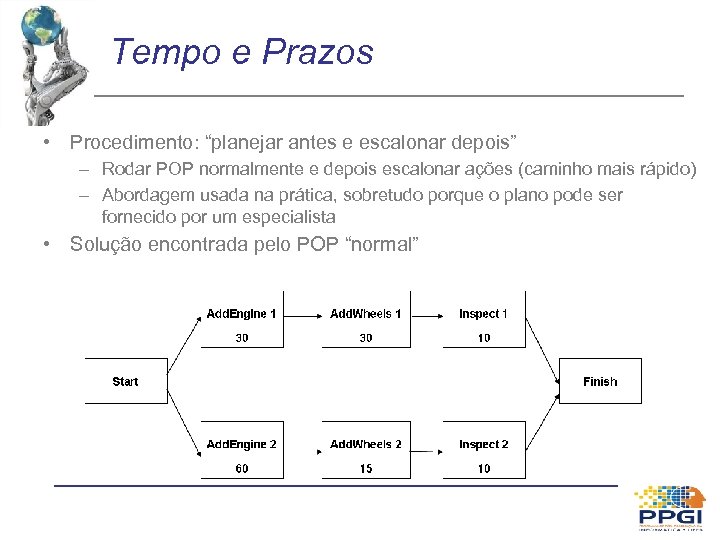
Tempo e Prazos • Procedimento: “planejar antes e escalonar depois” – Rodar POP normalmente e depois escalonar ações (caminho mais rápido) – Abordagem usada na prática, sobretudo porque o plano pode ser fornecido por um especialista • Solução encontrada pelo POP “normal”

Tempo e Prazos • Método do Caminho Crítico (CPM) – Caminho Crítico: caminho cujo tempo total é maior – Para cada ação, indicar » Tempo Mais Cedo de Início (ES – Earliest Start) » Tempo Mais Tarde de Início (LS – Latest Start) – Ações no caminho crítico não podem sofrer nenhum atraso – Ações fora desse caminho podem sofrer atrasos de tolerância LS - ES
![Tempo e Prazos [0, 15] Add. Engine 1 30 [30, 45] Add. Wheels 1 Tempo e Prazos [0, 15] Add. Engine 1 30 [30, 45] Add. Wheels 1](https://present5.com/presentation/6841f8c8c2caa2a0c8b6426fcb74a556/image-14.jpg)
Tempo e Prazos [0, 15] Add. Engine 1 30 [30, 45] Add. Wheels 1 30 [60, 75] Inspect 1 10 [0, 0] Start [85, 85] Finish [0, 0] Add. Engine 2 60 Caminho crítico [60, 60] Add. Wheels 2 15 [75, 75] Inspect 2 10
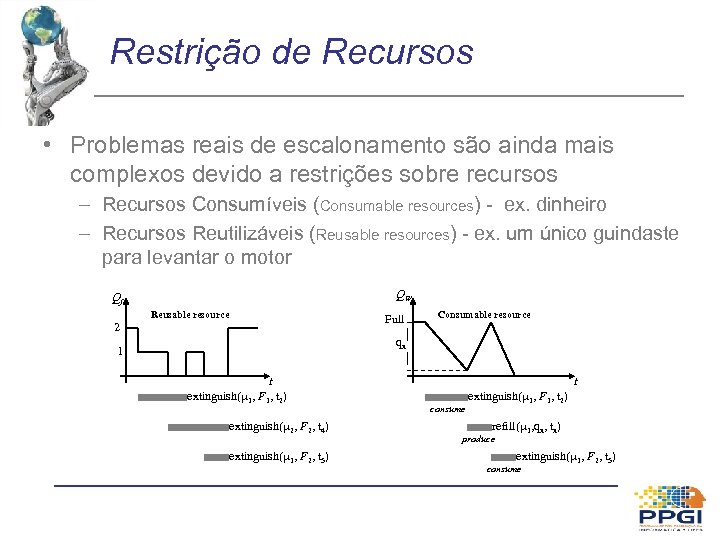
Restrição de Recursos • Problemas reais de escalonamento são ainda mais complexos devido a restrições sobre recursos – Recursos Consumíveis (Consumable resources) - ex. dinheiro – Recursos Reutilizáveis (Reusable resources) - ex. um único guindaste para levantar o motor QW Qf Reusable resource 2 Full Consumable resource qx 1 t extinguish( 1, F 1, t 2) extinguish( 2, F 2, t 4) extinguish( 1, F 2, t 5) t consume extinguish( 1, F 1, t 2) refill( 1, qx, tx) produce extinguish( 1, F 2, t 5) consume

Restrição de Recursos • Solução para recursos consumíveis – adicionar precondições e efeitos – Action (Add. Engine(e, c), Precond: Engine (e, c, d) Car(c) Engine. In(c) (Money(g) > 100) Effect: Engine. In(c) Duration(d) Money(g-100))

Restrição de Recursos • Solução para recurso reutilizável: – Mais complicado porque a quantidade de recursos permanece inalterada depois da ação! – Incrementar representação do problema para incluir novo campo » “Resource: R(k)”, k unidades de R são necessárias – Funciona tanto como » uma pré-condição (não se pode fazer sem ele) » um efeito temporário (indisponível pela duração da ação) • Voltando ao exemplo. . . – 1 guindaste, um macaco mecânico e 1 inspetor disponível

Exemplo: Montagem de Dois Carros Init (Car(C 1) Car(C 2) Engine(E 1, C 1, 30) Engine(E 2, C 2, 60) Wheels(W 1, C 1, 30) Wheels(W 2, C 2, 15) Engine. Hoists(1) Wheel. Stations(1) Inspectors(2) ) Goal (Done(C 1) Done(C 2) Action (Add. Engine(e, c, m), PRECOND: Engine(e, c, d) Car(c) Engine. In(c) EFFECT: Engine. In(c) Duration(d) RESOURCE: Engine. Hoist(1) ) Action (Add. Wheels(w, c), PRECOND: Wheels(w, c, d) Car(c) EFFECT: Wheels. On(c) Duration(d) RESOURCE: Wheel. Stations(1) ) Action (Inspect(c), PRECOND: Engine. In(c) Wheels. On(c) Car(c) EFFECT: Done(c) Duration(10) RESOURCE: Inspectors(1) )
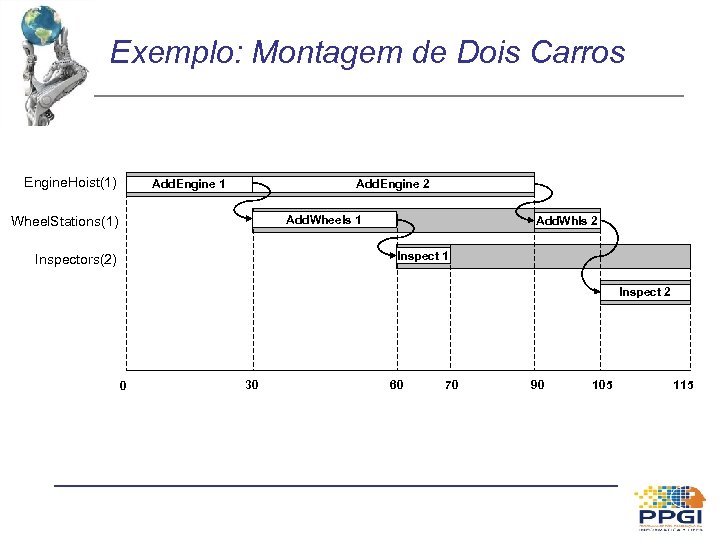
Exemplo: Montagem de Dois Carros Engine. Hoist(1) Add. Engine 1 Add. Engine 2 Wheel. Stations(1) Add. Wheels 1 Add. Whls 2 Inspect 1 Inspectors(2) Inspect 2 0 30 60 70 90 105 115
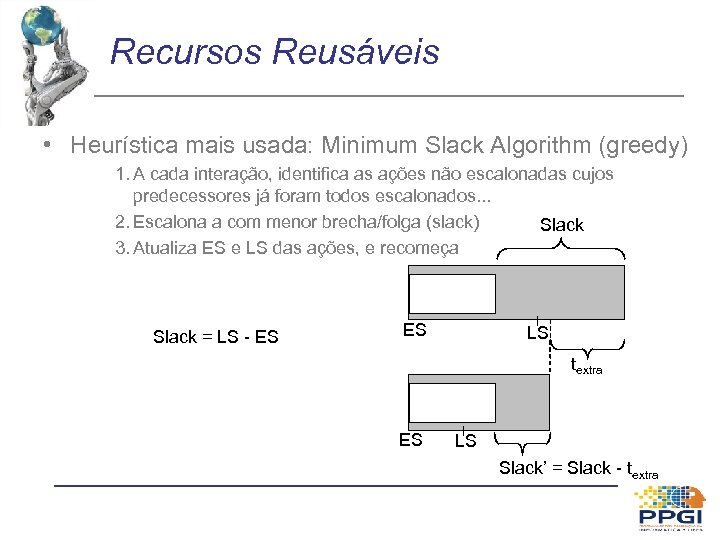
Recursos Reusáveis • Heurística mais usada: Minimum Slack Algorithm (greedy) 1. A cada interação, identifica as ações não escalonadas cujos predecessores já foram todos escalonados. . . 2. Escalona a com menor brecha/folga (slack) Slack 3. Atualiza ES e LS das ações, e recomeça Slack = LS - ES ES LS textra ES LS Slack’ = Slack - textra

Planejamento Hierárquico • Benefício de uma estrutura hierárquica – A cada nível a quantidade de tarefas é pequena comparada com o todo » Ex. planejamento militar e administrativo • De fato. . . – Instruções detalhadas provocam explosão combinatória » Ex. “Avançar(1 m), Girar(40°), . . . ” • Embora. . . – Instruções abstratas não são diretamente implementáveis no mundo real. » Ex. Go(Supermarket), Buy(Milk), Build(House)

Planejamento Hierárquico • Hierarchical Task Network (HTN) Planning – Planejar refinando um plano inicial completo apenas com decomposição hierárquica de operadores abstratos • Operadores – Primitivos: diretamente executáveis – Abstratos: não primitivos • Plan library – Contém várias decomposições de ações abstratas em menos abstratas ou mesmo planos inteiros pré-concebidos – Cada ação abstrata tem pré-condições e efeitos que são comuns a todas as instanciações dela
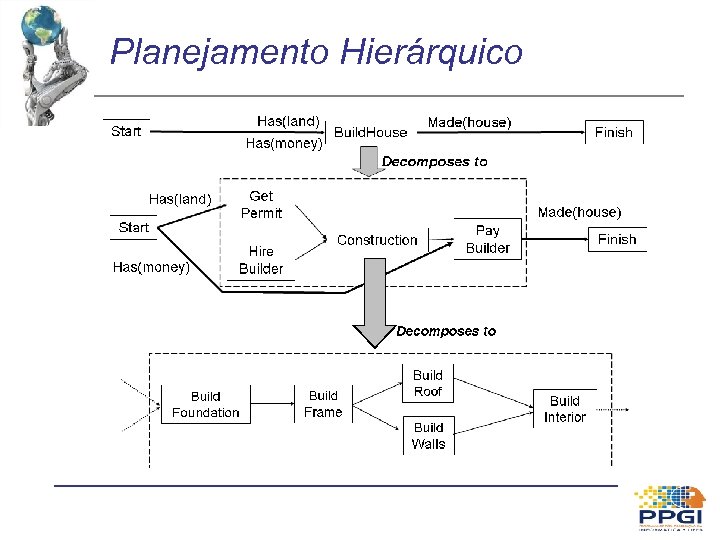
Planejamento Hierárquico

Planejamento Hierárquico • Planejamento hierárquico híbrido – Na prática, se mistura operadores de decomposição (HTN) com outros operadores padrão (POP) • Como implementa? • Estendendo/Redefinindo POP – Decomposição de operadores abstratos » c/ indicação de quem são ou não os operadores abstratos – Como decompor operadores não primitivos

Planejamento Hierárquico • Planejamento hierárquico híbrido – Na prática, se mistura operadores de decomposição (HTN) com outros operadores padrão (POP) • Como implementa? • Estendendo/Redefinindo POP – Decomposição de operadores abstratos » c/ indicação de quem são ou não os operadores abstratos – Como decompor operadores não primitivos

Planejamento Hierárquico • Operador Decompose( )

Planejamento Hierárquico • Algoritmo – Construir POP inicial ao maior nível de abstração – Recursivamente decompor ações abstratas até POP final conter apenas operadores primitivos (que podem ser executados pelo agente) – Resolver ameaças e verificar consistência global do POP final • Obs – Deve-se garantir que todo passo de um plano final P é primitivo • Decomposição d’ para a ação a’ – Tarefa realizada em 3 fases. . .
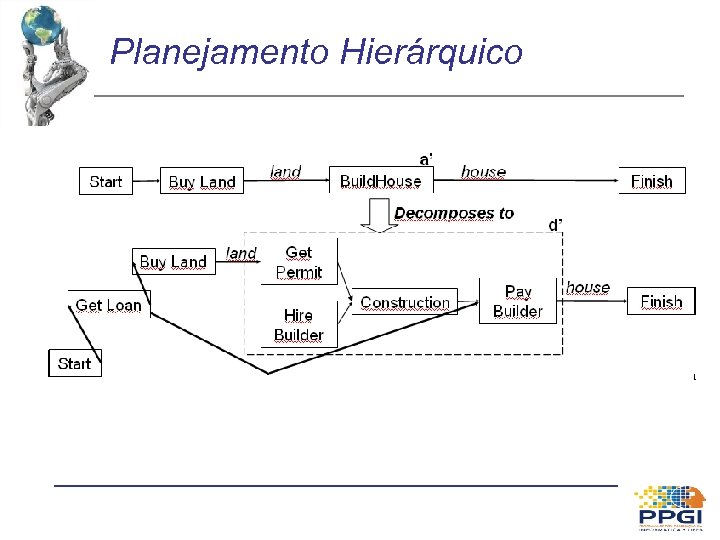
Planejamento Hierárquico

Planejamento Hierárquico • Fase 1: Substituir a’ por d’ – Remover a’ » ex. Build. House – Inserir cada passo de d’ – Transcrever restrições internas à d’ » ex. Get. Permit antes Contruction – Introduzir novos passos quando for o caso » ex. Get. Loan – Ou, eventualmente, reutilizar um passo já existente (chamado de compartilhamento) » ex. Get. Loan

Planejamento Hierárquico • Fase 2: Transcrever as restrições de ordenamento – Dado um passo qualquer B < a’ (ou B > a’), como ele fica em relação à d’? » solução 1: B antes (ou depois) de todos os passos de d’ => muito restritivo, pois Buy. Land não precisa vir antes de Hire. Builder » solução 2: menor engajamento • Fase 3: Ligações causais – Se B p a’, troque ela por um conjunto de ligações para todos os passo de d’ contendo a pré-condição p » Ex. Buy. Land land Build. House, é substituído por Buy. Land – Idem para as ligações causais do tipo a’ p C land Permit

Planejamento Hierárquico • Vantagens de Sub-POPs independentes: – espaço de busca reduzido – conhecimento composicional – uso e reuso de sub-POPs pré-planejado

Aplicações Industriais (Job Shop) • Sistema Tosca na Hitachi – Planejamento mensal para 350 produtos diferentes, 35 máquinas de montagem, mais de 2000 operações – Menor engajamento (ex. classe de máquina a ser usada) • Sistema Isis na Westinghouse – Milhares de lâminas de turbinas e várias máquinas de montagem – O tempo atribuído depende da prioridade do pedido – Menor engajamento, planejamento hierárquico

Aplicações Espaciais • Sistema Optimun-AIV – Montagem, integração e verificação de aeronaves – Gera planos, monitora execução (feita por seres humanos) e replaneja rapidamente – Melhor que Pesquisa Operacional para problemas complexos pois pode replanejar automaticamente – Implementado com O-Plan (Currie & Tate 91) que estende POPStrips (+ tempo, recursos e hierarquia)
6841f8c8c2caa2a0c8b6426fcb74a556.ppt