Description of Interactive Modeling Simulation Animation and Real-Time

Description of Interactive Modeling, Simulation, Animation, and Real-Time Control (Mo. SART) Aircraft Environment Tae-Young Kim Richard P. Metzger, Jr. Chen-l Lim Armando A. Rodriguez ASEE Pacific Southwest Meeting `99 Saturday, March 20 th 1999 Harrah’s Hotel Las Vegas, Nevada Ack : White House , NSF, WAESO/CIMD, Boeing, Intel, Microsoft, CADSI, Knowledge Revolution, Math. Works, Lego, Xilinx, Honeywell, National Instruments, Integrated Systems, ASU CIEE. http: //www. eas. asu. edu/~aar/research/mosart

Outline • Motivation • Mathematical Models • Control Laws • Environment • Utility • Summary & Future Directions

Motivation • MIMO Aircraft Control Design - High Performance Extensive Coupling • Need Advanced Analysis, Design, and Visualization Tools

Aircraft Mathematical Models

Longitudinal Pitch Dynamics. x= Ax + Bu y= Cx u (Inputs) y (Outputs) ele (Elevator) rpm (Engine rpm) (Pitch) v v x (States) (Speed) (Alpha) . (Pitch) (Pitch rate) (Speed)

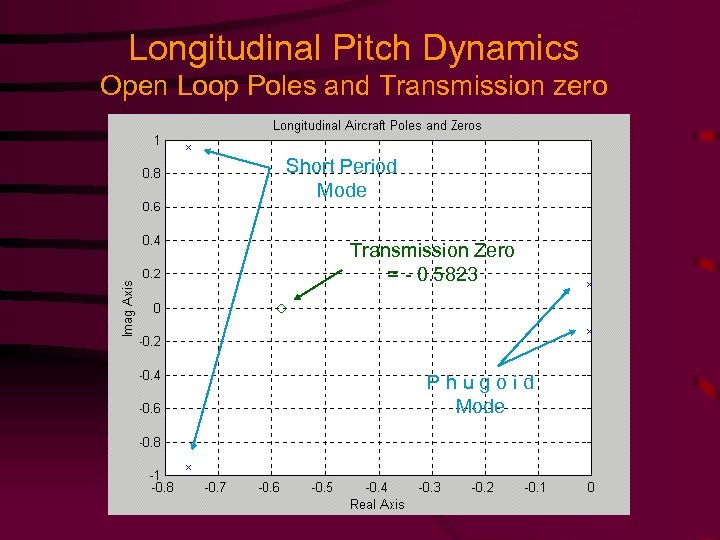Longitudinal Pitch Dynamics Open Loop Poles and Transmission zero Short Period Mode Transmission Zero = - 0. 5823 Phugoid Mode

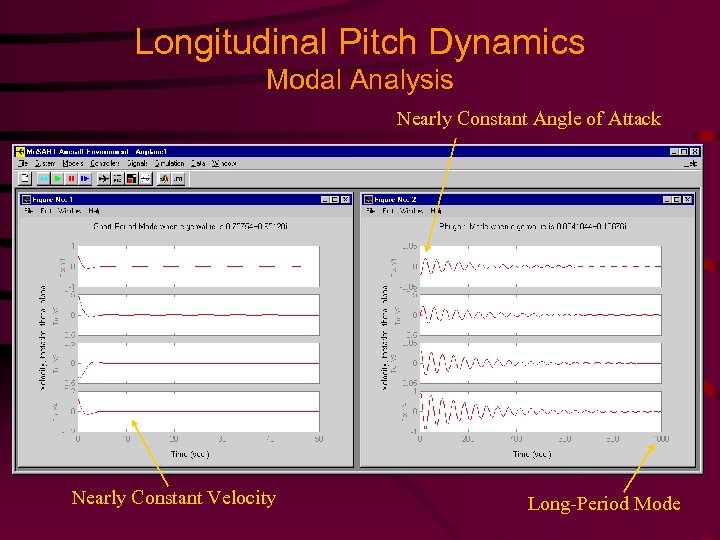Longitudinal Pitch Dynamics Modal Analysis Nearly Constant Angle of Attack Nearly Constant Velocity Long-Period Mode

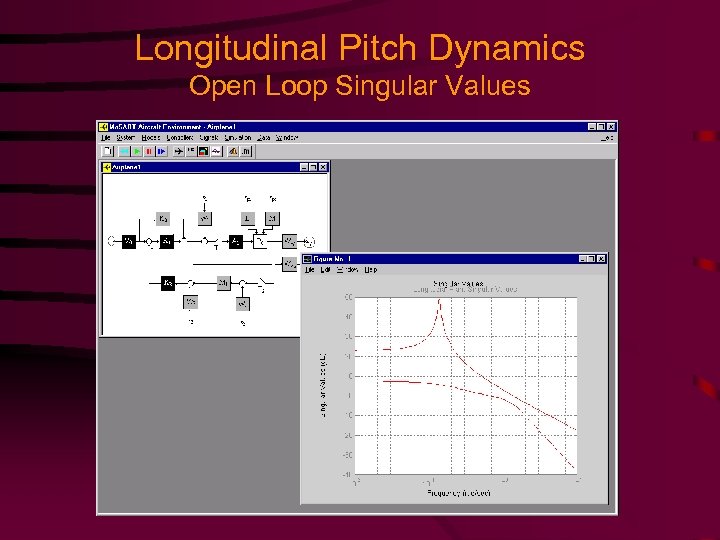Longitudinal Pitch Dynamics Open Loop Singular Values

Lateral (Roll - Yaw Rate) Dynamics. x= Ax + Bu y= Cx u (Inputs) y (Outputs) ail (Aileron) (Roll angle) rud (Rudder) . (Yaw Rate) . (Roll rate) x (States) (Roll). (Yaw rate) (Side Slip Angle)

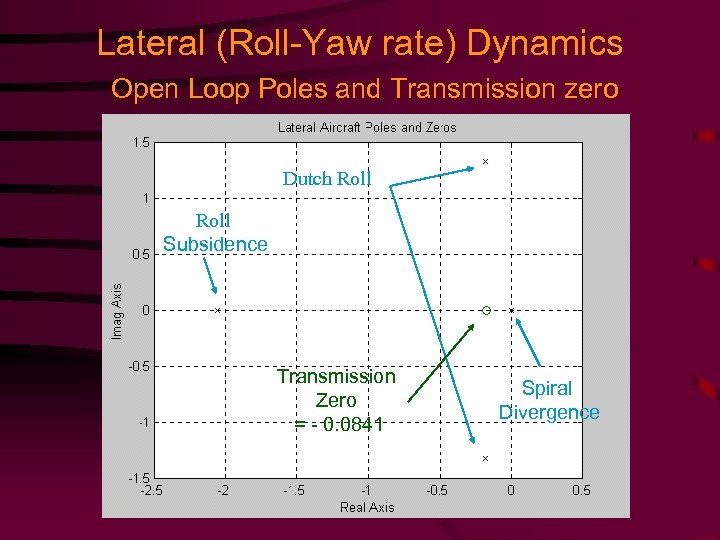Lateral (Roll-Yaw rate) Dynamics Open Loop Poles and Transmission zero Dutch Roll Subsidence Transmission Zero = - 0. 0841 Spiral Divergence

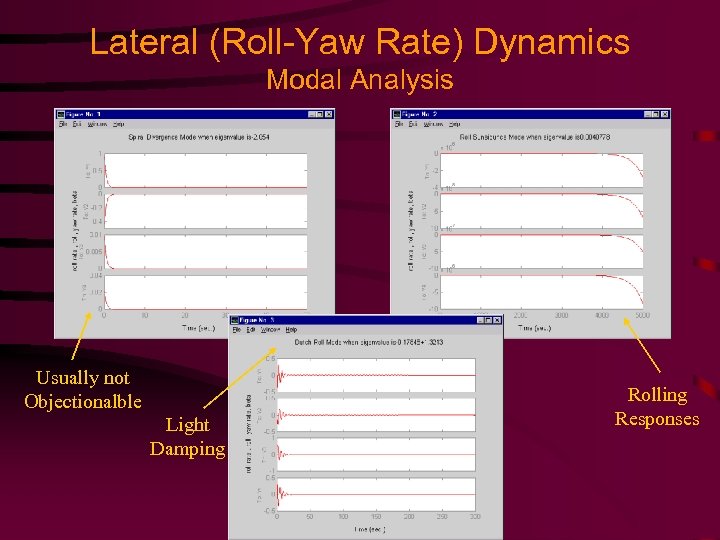Lateral (Roll-Yaw Rate) Dynamics Modal Analysis Usually not Objectionalble Light Damping Rolling Responses

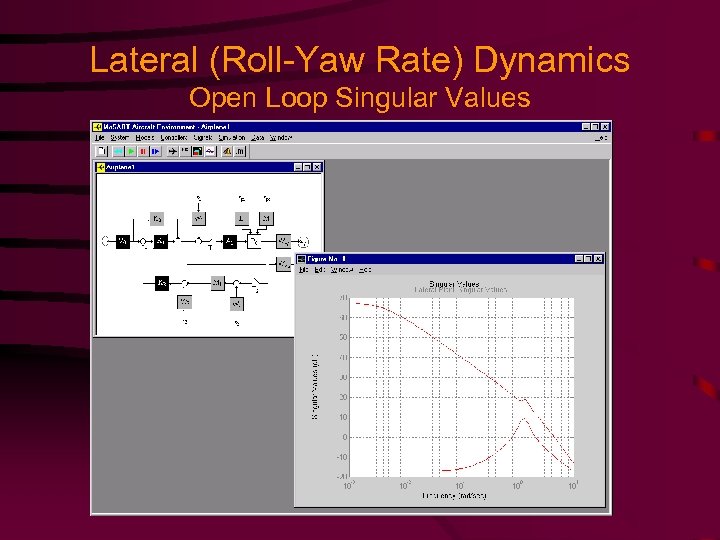Lateral (Roll-Yaw Rate) Dynamics Open Loop Singular Values

Control Laws

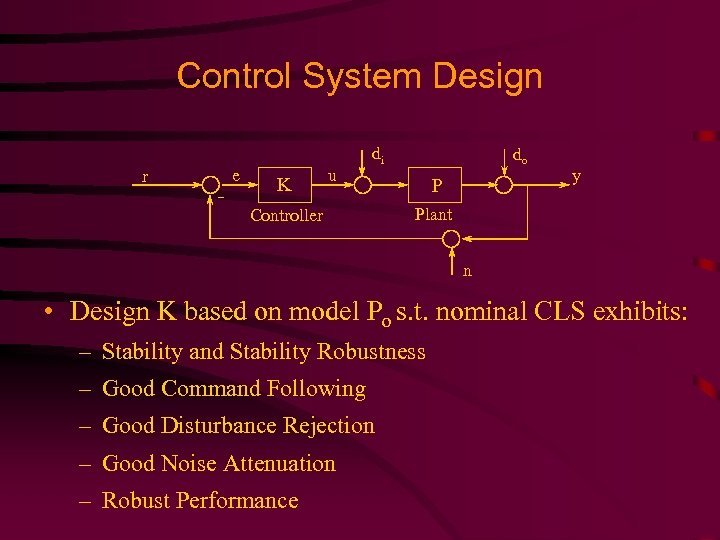Control System Design r e K u di Controller do P y Plant n • Design K based on model Po s. t. nominal CLS exhibits: – Stability and Stability Robustness – Good Command Following – Good Disturbance Rejection – Good Noise Attenuation – Robust Performance

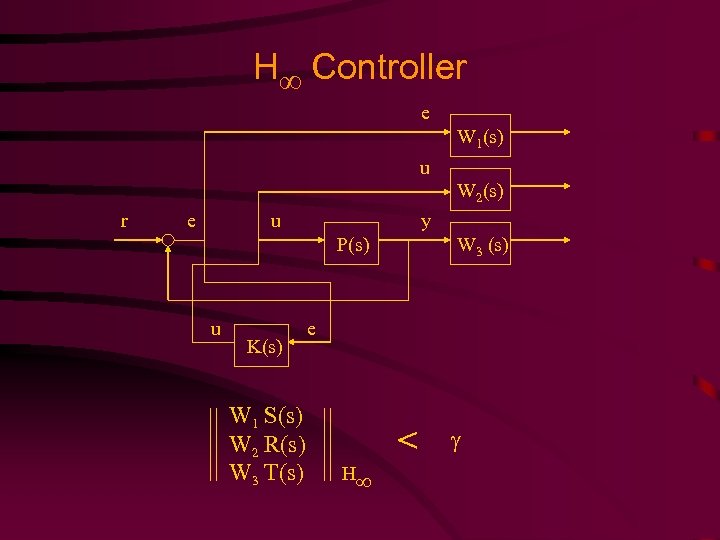H Controller e W 1(s) u W 2(s) r e u y P(s) u K(s) W 1 S(s) W 2 R(s) W 3 T(s) W 3 (s) e < H

H Norm W 1 S(s) W 2 R(s) W 3 T(s) = max H W 1 S(j ) W 2 R(j ) W 3 T(j )

Longitudinal (Pitch) Dynamics : W 1, W 2, and W 3 = 0. 6337 = 1/1. 5781 W 1 (s) = d i a g W 2 (s) = d i a g W 3 (s) = d i a g (s + 1. 3 s + 0. 22)(s + 0. 0001) 1. 3 , 1. 3 0. 6337 0. 01 , 0. 6337(s + 0. 0001) 2

Longitudinal (Pitch) Dynamics : Complementary Sensitivity : T = [I + PK]-1 PK

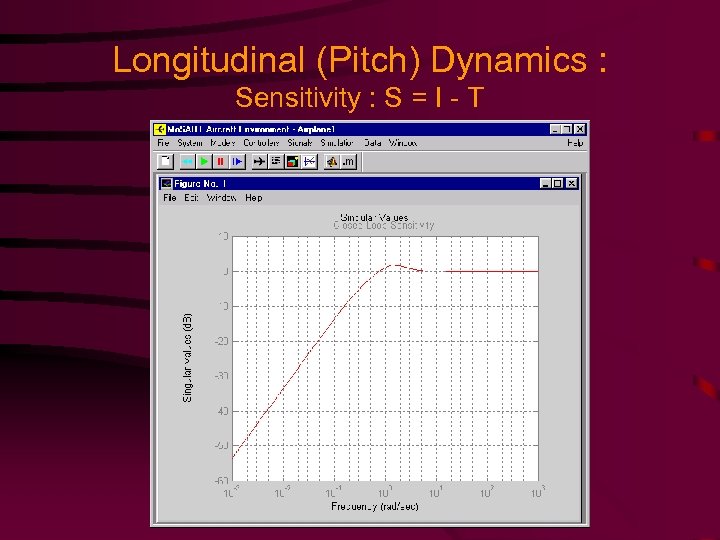Longitudinal (Pitch) Dynamics : Sensitivity : S = I - T

Longitudinal (Pitch) Dynamics : Reference command Following [ v] = [ 1 0 ] [ v] = [ 0 1 ]

Lateral (Roll- Yaw rate) Dynamics : W 1, W 2, W 3 and = 0. 7574 = 1/1. 3203 W 1 (s) = d i a g W 2 (s) = W 3 (s) = diag (s + 1)(s + 0. 0001) 1 , 1 0. 7574 0. 01 , 0. 7574(s + 04) (s + 0. 0001) , 0. 7574(s + 0. 4) (s + 0. 0001)

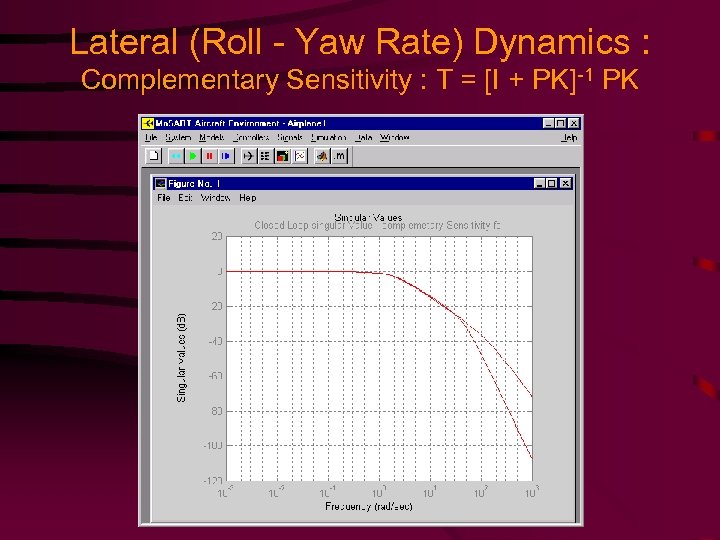Lateral (Roll - Yaw Rate) Dynamics : Complementary Sensitivity : T = [I + PK]-1 PK

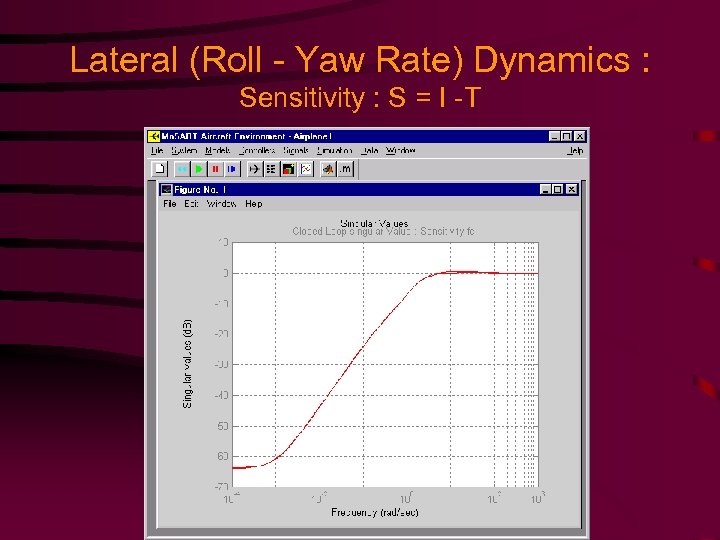Lateral (Roll - Yaw Rate) Dynamics : Sensitivity : S = I -T

Lateral (Roll - Yaw Rate) Dynamics : Reference command Following . [ ] = [1 0] . [ ] = [0 1]

Environment Structure • Program User Interface UI) (P IM) • Simulation Module (S AM) • Graphical Animation Module (G OM) • Communications Module (C • Help-Instruct Module IM) (H

Utility of Environment SIMULINK Driven 3 D Animation Environment : Evaluation of H Design

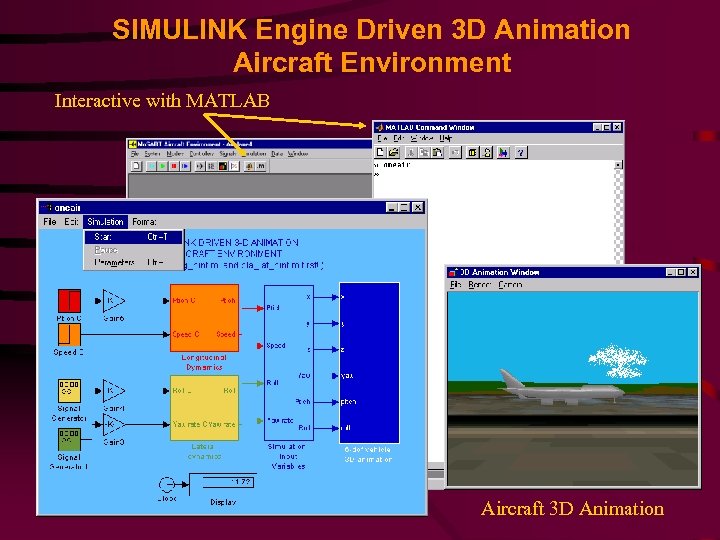SIMULINK Engine Driven 3 D Animation Aircraft Environment Interactive with MATLAB Aircraft 3 D Animation

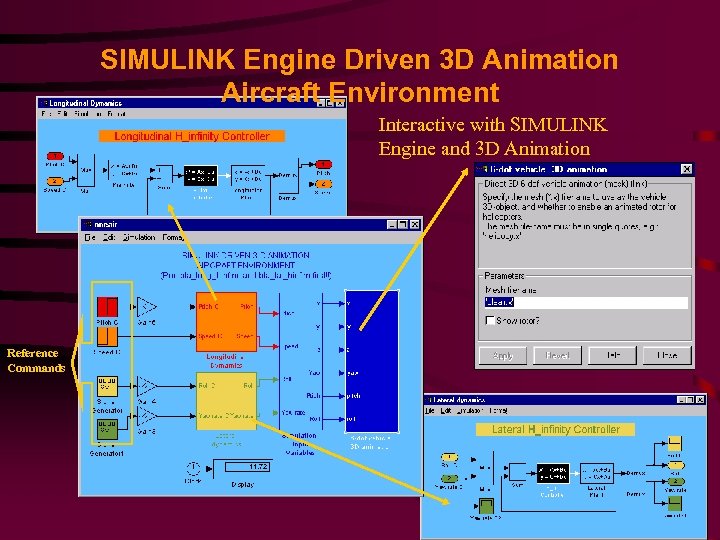SIMULINK Engine Driven 3 D Animation Aircraft Environment Interactive with SIMULINK Engine and 3 D Animation Reference Commands

Summary • Versatile system-specific interactive Mo. SART environments • • Windows / C++ / Direct-X / MATLAB User friendly: accessible & intuitive User can alter model structures & parameters Highly extensible: ability to incorporate new simulation/animation models

Future Directions More visual indicators Advanced SIM and GAM Expanded HIM: web support, multimedia Enhanced integration with MATLAB Integrated design & analysis environment … development of Mo. SART Facility at ASU Online presentation available at: Visit Mo. SART facility web site: http: //www. eas. asu. edu/~aar/research/mosart/Presentations