Derivation and Application of Nonlinear Analytical Redundancy Techniques

Derivation and Application of Nonlinear Analytical Redundancy Techniques with Applications to Robotics M. L. Leuschen Thesis Defense 22 October, 2001

Overview l Analytical redundancy (AR): A powerful technique for fault detection » Review of standard linear AR (LAR) techniques Derive novel nonlinear AR (NLAR) technique using nonlinear observability l NLAR application and results l Conclusions and future work l

Motivation Robotic fault detection an important issue due to circumstances in which robots are used l Many robots have significant nonlinearities l Nonlinear systems degrade the efficiency of linear model-based fault detection schemes such as AR l

Contribution of Thesis Standard LAR methods inappropriate for nonlinear systems l Modern nonlinear control methods were applied to develop a accurate new nonlinear analytical redundancy (NLAR) l NLAR tested on physical and simulated systems l » Compares favorably to LAR

Previous Work Visinsky: Linear AR for electrical robots l Wunnenberg/Frank: Linear observers and AR for conventional robot dynamics l Starosweicki/Comtet-Varga: Nonlinear AR relations for certain nonlinear systems without observability based guarantees l

Analytical Redundancy (AR) l First described by Chow and Willsky. (IEEE Transactions on Automatic Control, July, 1984. ) l Rigorous Formal Method: » » Tests based on left null-space of the observability matrix, giving greatest possible number of independent tests Typical result uses time history of sensor data to test model equations, higher order dynamic response, as well as sensor redundancies

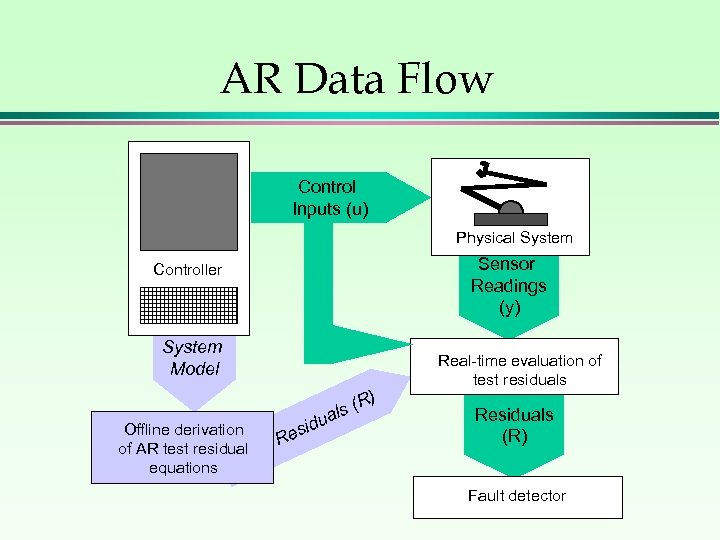AR Data Flow Control Inputs (u) Physical System Sensor Readings (y) Controller System Model Offline derivation of AR test residual equations R d esi (R) s ual Real-time evaluation of test residuals Residuals (R) Fault detector

AR Structure l Core Concept: » Find left null-space of canonical observability » Take product of null-space and input-output formulation of observability to derive tests

Linear AR (LAR) Standard continuous-time linear control model, n states, q inputs, m sensors: Calculate the left null-space: Canonical observability submatrices for standard linear system:

LAR Dynamically Derived Observability Restate observability matrix in terms of known quantities: For fault-free system, dynamically derived observability is equivalent to standard linear observability times the state vector:

How Many LAR Tests? l In Linear AR, the Cayley-Hamilton theorem is used to determine the number of independent tests: l Extra sensors (increases m, additional CL(j)’s) result in more tests

Null-Space AR Tests System LAR Example DD Observability R 1 is the first model equation R 2 is the derivative of R 1 R 3 is the second model equation R 4 is the derivative of R 3

Initial Approach: Nearly Nonlinear AR (NNAR) Nonlinear systems better modeled by using several linearizations over local regions l Taking the limit as region size goes to zero will produce nonlinear tests l Limitation: The observability used is approximate l » Number of tests and coverage of tests is ad hoc

NLAR: a Nonlinear Observability Based Approach AR adapted using nonlinear control theory to develop accurate Nonlinear Analytical Redundancy method (NLAR) l Superior to previous methods l » Follows nonlinear model, unlike LAR » Uses full observability space, unlike NNAR l Nontrivial to derive » Nonlinear systems lack useful principles such as superposition

Observability for Nonlinear Systems (Isidori) Standard continuous nonlinear control model; n states, q inputs, m sensors: Nonlinear observation space for this system is: is the Lie derivative l If rank(grad( )) = n (the system rank), the system is ‘locally observable’

A Reformulated Nonlinear Observability for AR Normal nonlinear not suitable for NLAR- Unable to construct a dynamically derived observability! l Triangular Nonlinear Observability l Where:

Nonlinear Dynamically Derived Observability l Express in an input-output format: l Repeated derivatives of y, similar to LAR

Number of NLAR Tests Cayley-Hamilton does not apply to nonlinear systems l However, we have shown that the number of independent NLAR tests is: l - number of states - number of sensors - j th sub-matrix of

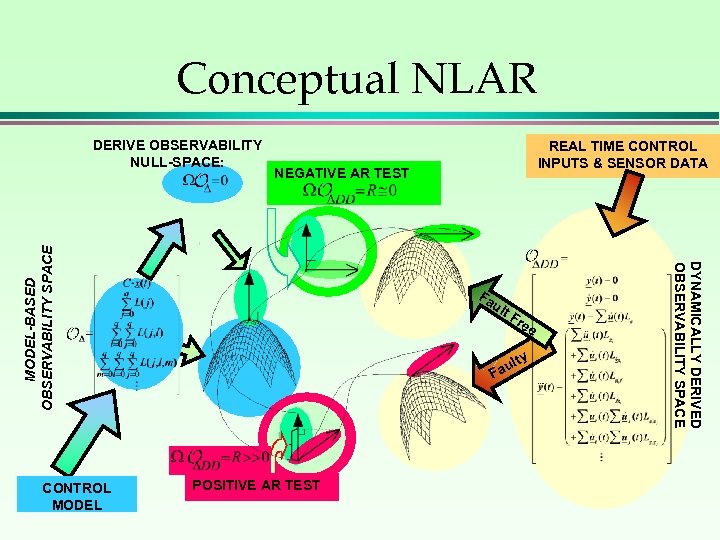Conceptual NLAR Fa ult Fr ee y ult Fa POSITIVE AR TEST DYNAMICALLY DERIVED OBSERVABILITY SPACE CONTROL MODEL REAL TIME CONTROL INPUTS & SENSOR DATA NEGATIVE AR TEST MODEL-BASED OBSERVABILITY SPACE DERIVE OBSERVABILITY NULL-SPACE:

The Rosie Mobile Worksystem L. C. Bares, L. S. Conley, and B. R. Thompson. Rosie: A Mobile Worksystem for D&D: Overview of System Capabilities and CP-5 Reactor Application. In Proceedings of the ANS 7 th Topical Meeting on Robotics and Remote Systems, pages 471 -477 L. Conley, W. R. Hamel, and B. R. Thompson. Rosie: A Mobile Worksystem for Decontamination and Dismantlement Operations. In Proceedings of the ANS 6 th Topical Meeting on Robotics and Remote Systems, pages 231 -238

The Rosie Hydraulic Testbed l Physical testbed based on the Rosie mobile worksystem, a decommissioning robot built for DOE p. S Control Valve Motor . (k) m pl (k) xv

NLAR Tests System Rosie NLAR R 1 is the first model equation, R 2 is the derivative of R 1, R 3 is the second model equation, R 4 is the derivative of R 3

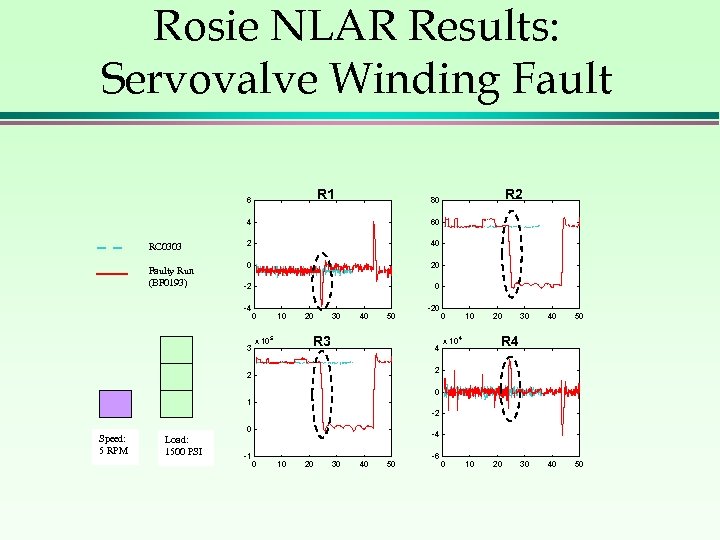Rosie NLAR Results: Servovalve Winding Fault R 1 6 4 RC 0303 Faulty Run (BF 0193) R 2 80 60 2 40 0 20 -2 0 -4 3 0 10 20 30 40 50 R 3 x 10 5 -20 4 0 10 20 30 40 50 R 4 x 10 4 2 2 0 1 -2 Speed: 5 RPM 0 Load: 1500 PSI -1 -4 0 10 20 30 40 50 -6 0 10 20

The Integrated Motion Inc. Robot W. E. Dixon, I. D. Walker, Darren M. Dawson, J. P. Hartranft. Fault Detection for Robot Manipulators with Parametric Uncertainty: A Prediction-Error-Based Approach. IEEE Transactions on Robotics and Automation, 16(6): 689 -699, 2001.

NLAR for the IMI Robot l A two joint planar manipulator at Clemson University » Canonical robot example » Many interesting nonlinearities l Extensively modeled for dynamic control » Control model used to derive NLAR tests » Control model converted to simulation to generate copious data quickly

IMI Robot Model Equations pi are inertias, fi are frictions, qi are joint positions, and ui are control input torques

IMI Robot NLAR Tests l NLAR test residuals complex, stated here in terms of the model equations

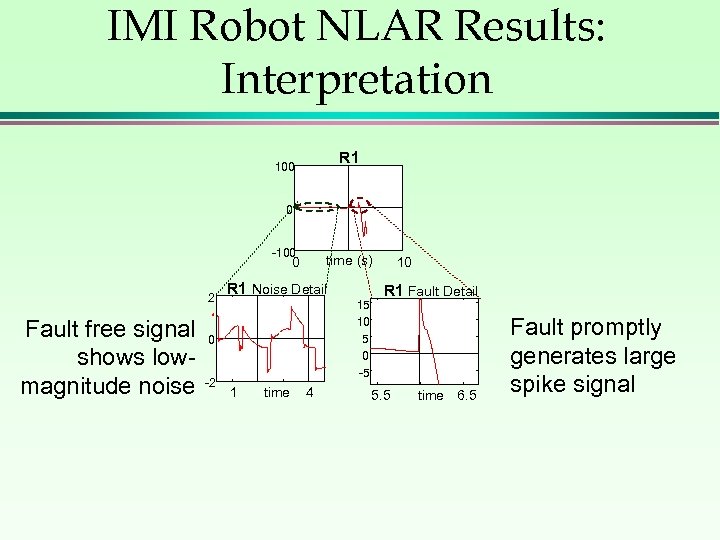IMI Robot NLAR Results: Interpretation R 1 100 0 -100 time (s) 0 2 Fault free signal shows lowmagnitude noise R 1 Noise Detail 0 -2 1 time 4 15 10 5 0 -5 10 R 1 Fault Detail 5. 5 time 6. 5 Fault promptly generates large spike signal

IMI Robot NLAR Results: Frozen Elbow Sensor Fault R 1 100 1 4 x 10 R 2 1 6 x 10 R 3 20 0 time (s) 10 R 7 400 -1 0 10000 0 time (s) 10 R 8 -2 0 0. 5 time (s) 10 R 9 -10 0 10 5000 200 time (s) 10 -5000 0 R 6 R 10 5 time (s) x 105 10 -1 0 time (s) R 11 0 0 -10 0 -200 0 4 x 10 0 -100 0 1 0 0 -100 0 R 5 100 10 -1 0 R 4 time (s) 10 -0. 5 0 time (s) 10 -20 0 time (s) 10 -5 0 time (s) 10 Elbow resolver freezes at t=6 s l This fault is subtle, yet is still detected in one or two steps by most NLAR tests l 10

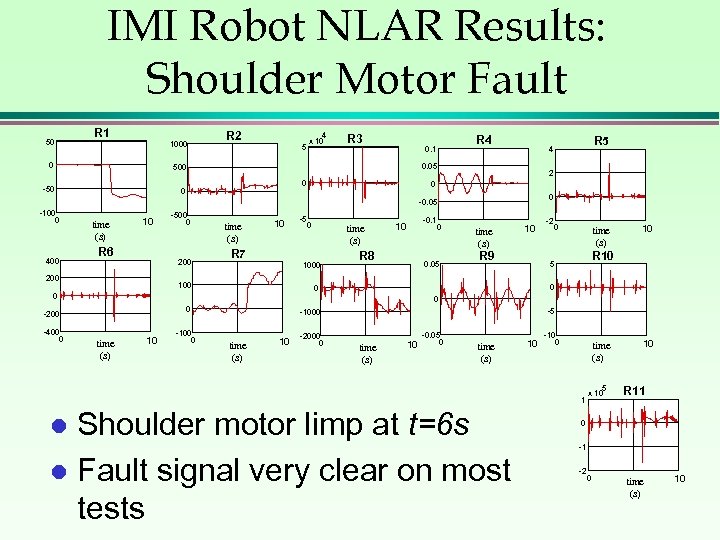IMI Robot NLAR Results: Shoulder Motor Fault 50 R 1 1000 0 R 2 5 4 x 10 R 3 0. 1 0 0 2 0 0 -0. 05 -100 0 400 time (s) 10 R 6 -500 0 200 time (s) 10 0 time (s) R 7 1000 100 -0. 1 0 10 R 8 0. 05 time (s) 10 R 9 -2 0 time (s) 0 0 0 -200 time (s) 10 -100 0 -5 -1000 time (s) 10 -2000 0 time (s) 10 -0. 05 0 time (s) 10 -10 0 time (s) 1 Shoulder motor limp at t=6 s l Fault signal very clear on most tests l 10 R 10 5 0 0 -400 0 -5 R 5 4 0. 05 500 -50 R 4 5 x 10 10 R 11 0 -1 -2 0 time (s) 10

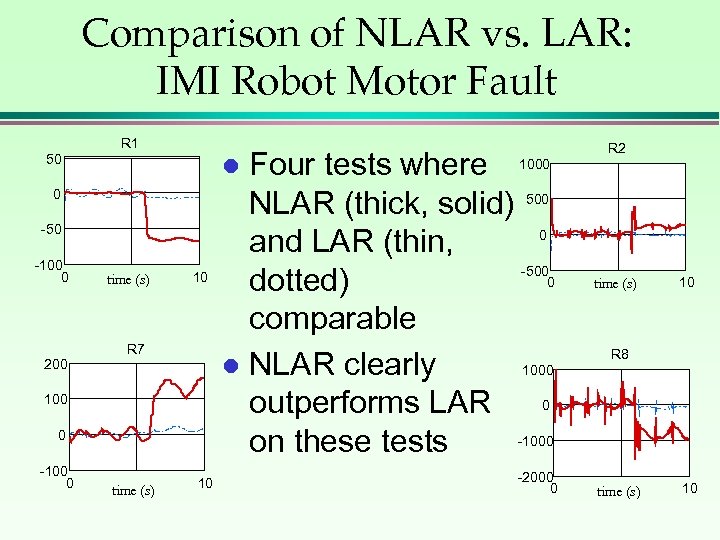Comparison of NLAR vs. LAR: IMI Robot Motor Fault R 1 50 0 -50 -100 0 time (s) 10 R 7 200 100 0 -100 0 Four tests where 1000 NLAR (thick, solid) 500 0 and LAR (thin, -500 0 dotted) comparable 1000 l NLAR clearly 0 outperforms LAR -1000 on these tests l time (s) 10 -2000 0 R 2 time (s) 10 R 8 time (s) 10

Summary and Conclusions Our new nonlinear analytical redundancy technique (NLAR) is a powerful modelbased fault detection method for nonlinear systems l NLAR a clear improvement over LAR l NLAR shows excellent results on our example nonlinear systems l

Contributions l New nonlinear analytical redundancy (NLAR) technique for fault detection in nonlinear systems » Reformulated nonlinear observability for NLAR null matrix determination » Nonlinear dynamically derived observability » Calculation of number of valid NLAR tests l Application of NLAR to test robots » Automatic calculation of NLAR tests

Directions for Future Work Further testing on data from physical testbeds and systems l Analysis of test residuals l » Thresholding and sensitivity » Fault classification Non smooth nonlinearities l Automated NLAR software package l

The End

Appendix: Additional Information

Rosie Details Foster-Miller testbed is based on the Rosie mobile worksystem, a decommissioning robot built for DOE l Wheeled platform with heavy-duty robotic manipulator l Central hydraulic power source l Wheel actuators of special interest to prevent failures that trap robot l

Physical Testbed l Collaborating with Foster-Miller Technologies Incorporated (FM) » Considerable experience in evaluating the reliability of hydraulic systems » Contracted by DOE to examine hydraulic fault issues for hazardous environments l FM constructed physical testbed to acquire fault data » Faults simulated by modifications to test rig

Hydraulic Test Rig

Dynamic Model Flow Equation: Linearized Flow: Torque Equation:

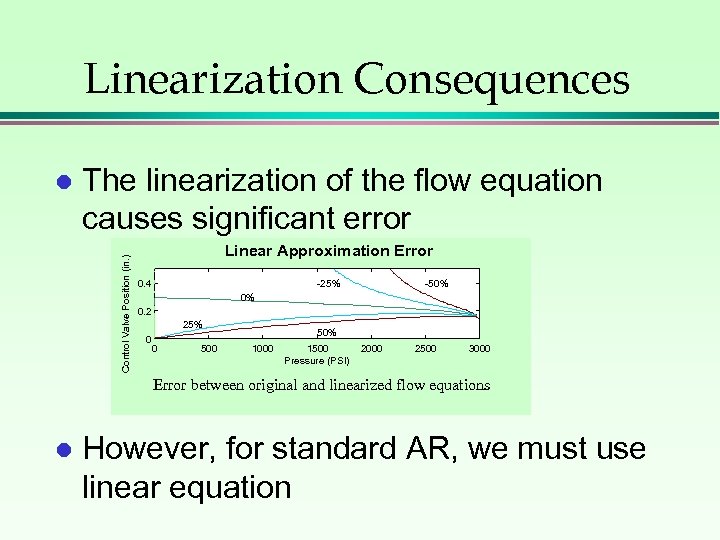Linearization Consequences The linearization of the flow equation causes significant error Control Valve Position (in. ) l Linear Approximation Error 0. 4 -25% -50% 0% 0. 2 25% 0 0 50% 1000 1500 Pressure (PSI) 2000 2500 3000 Error between original and linearized flow equations l However, for standard AR, we must use linear equation

Linear System AR Tests

Linear AR Test Characteristics V 1 and V 3 are the original discrete-time model equations l V 2 and V 4 are related to the first derivatives of V 1 and V 3 respectively, but use both model equations l More AR tests than model equations! l However, linearization of flow equation severely degrades performance l

Idea: Piecewise Linear Division of Workspace 3000 PSI Pressure Linearization Points Transition Regions -3000 PSI -0. 5 in. Valve Position 0. 5 in. Piecewise linear division of workspace

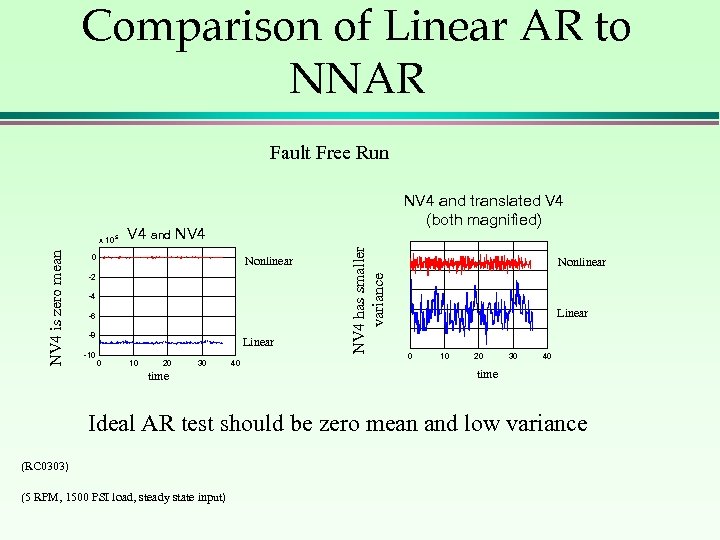Comparison of Linear AR to NNAR Fault Free Run V 4 and NV 4 0 Nonlinear -2 -4 -6 -8 -10 Linear 0 10 20 30 time 40 NV 4 has smaller variance NV 4 is zero mean x 10 5 NV 4 and translated V 4 (both magnified) Nonlinear Linear 0 10 20 30 40 time Ideal AR test should be zero mean and low variance (RC 0303) (5 RPM, 1500 PSI load, steady state input)

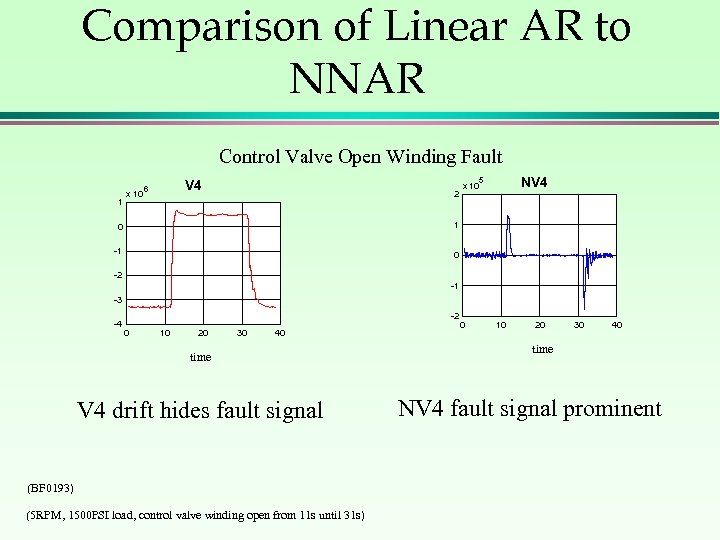Comparison of Linear AR to NNAR Control Valve Open Winding Fault 1 x 10 NV 4 5 V 4 6 2 0 1 -1 x 10 0 -2 -1 -3 -4 -2 0 10 20 30 40 time V 4 drift hides fault signal (BF 0193) (5 RPM, 1500 PSI load, control valve winding open from 11 s until 31 s) 0 10 20 30 40 time NV 4 fault signal prominent

Why go Beyond NNAR? l Nonlinear extension works better than linear, but it is not rigorous » Linear model used to derive basic tests » Essentially looking at AR for system linearized about current point of operation l Want to examine nonlinear equivalent to the observability space complement idea in AR

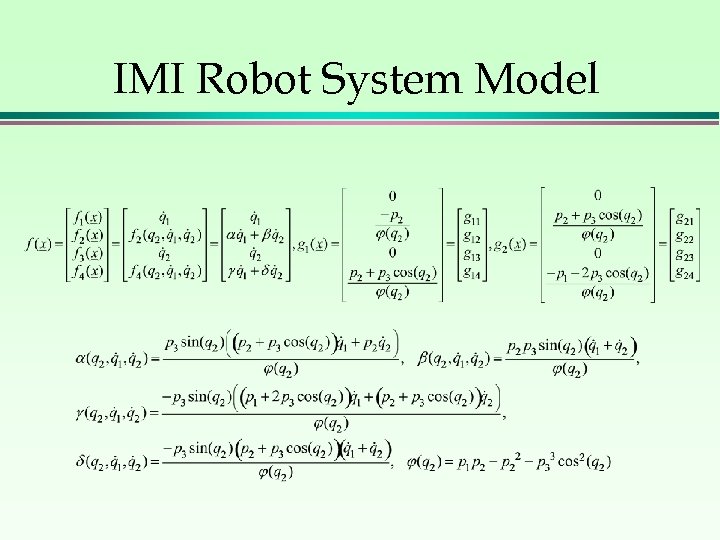IMI Robot System Model

IMI Fault Run Details Input signal: Example Test Residuals: