Деревья и их представление в STL Презентацию подготовила

Деревья и их представление в STL Презентацию подготовила Чиркова Ольга, 2 подгруппа, группа 271 ПИ

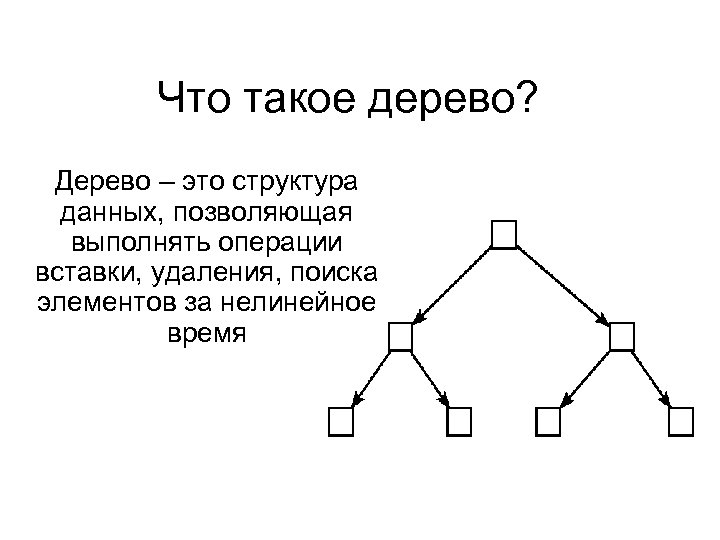Что такое дерево? Дерево – это структура данных, позволяющая выполнять операции вставки, удаления, поиска элементов за нелинейное время

Основные понятия: • Только одна вершина дерева не имеет предков – корень. • Все вершины, кроме корня, имеют единственного предка. • Вершины, не имеющие детей – листья. • Высота дерева – наибольшее число вершин от листа до корня. • Из любой вершины можно добраться до корня, последовательно перебираясь от одной вершины к ее предку, единственным путем.

Примеры деревьев: • Файловая система; • Иерархия в организациях (начальник подчиненные); • Генеалогическое дерево.

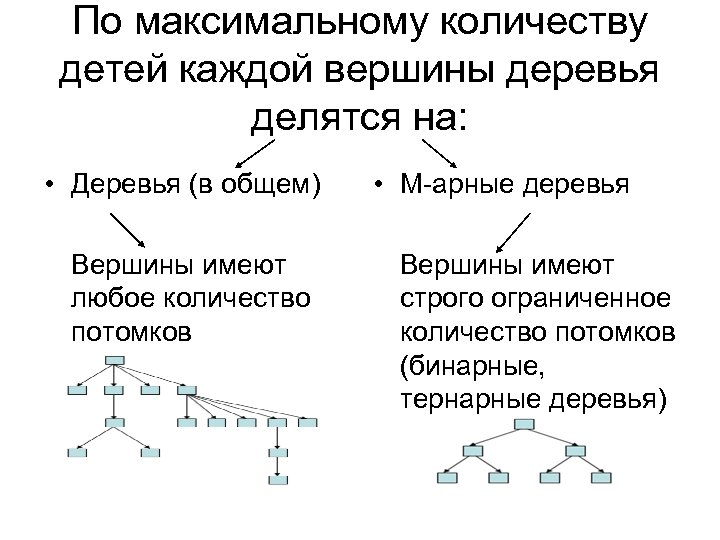По максимальному количеству детей каждой вершины деревья делятся на: • Деревья (в общем) Вершины имеют любое количество потомков • М-арные деревья Вершины имеют строго ограниченное количество потомков (бинарные, тернарные деревья)

Двоичные деревья Двоичное дерево – это M-арное дерево, у которого M=2. Куча (heap) – дерево, содержащее элементы либо в порядке убывания, либо в порядке возрастания.

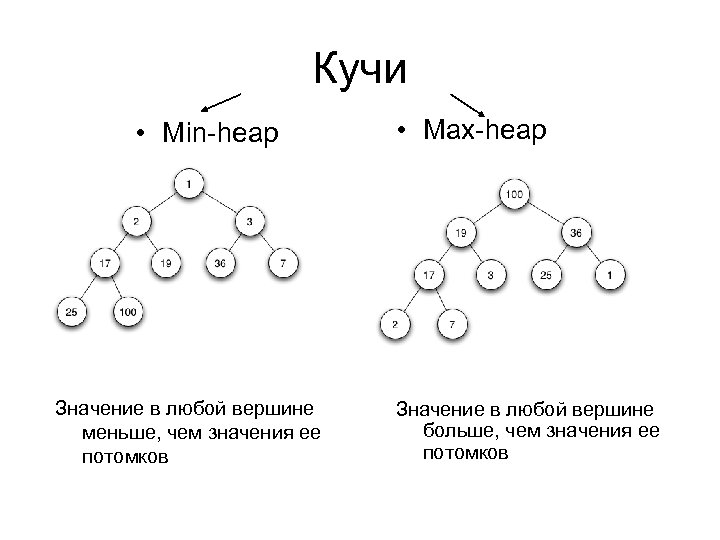Кучи • Min-heap Значение в любой вершине меньше, чем значения ее потомков • Max-heap Значение в любой вершине больше, чем значения ее потомков

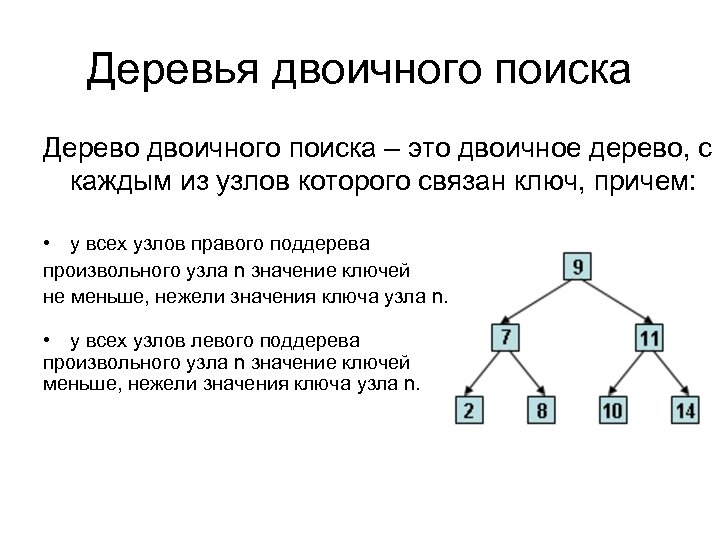Деревья двоичного поиска Дерево двоичного поиска – это двоичное дерево, с каждым из узлов которого связан ключ, причем: • у всех узлов правого поддерева произвольного узла n значение ключей не меньше, нежели значения ключа узла n. • у всех узлов левого поддерева произвольного узла n значение ключей меньше, нежели значения ключа узла n.

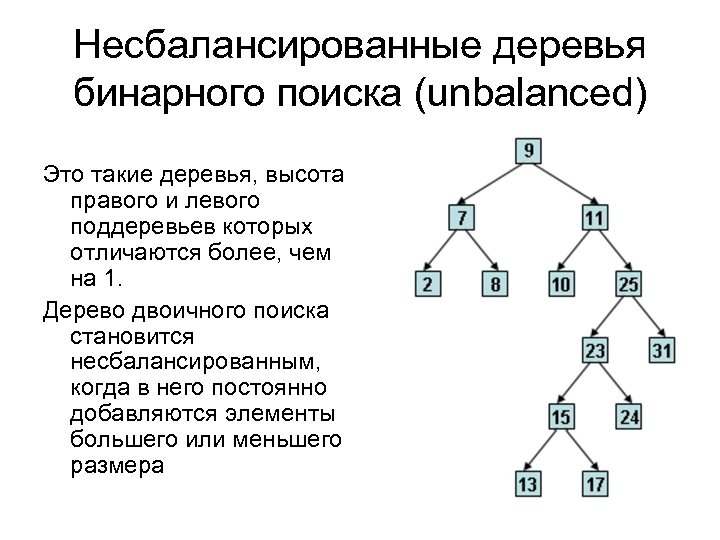Несбалансированные деревья бинарного поиска (unbalanced) Это такие деревья, высота правого и левого поддеревьев которых отличаются более, чем на 1. Дерево двоичного поиска становится несбалансированным, когда в него постоянно добавляются элементы большего или меньшего размера

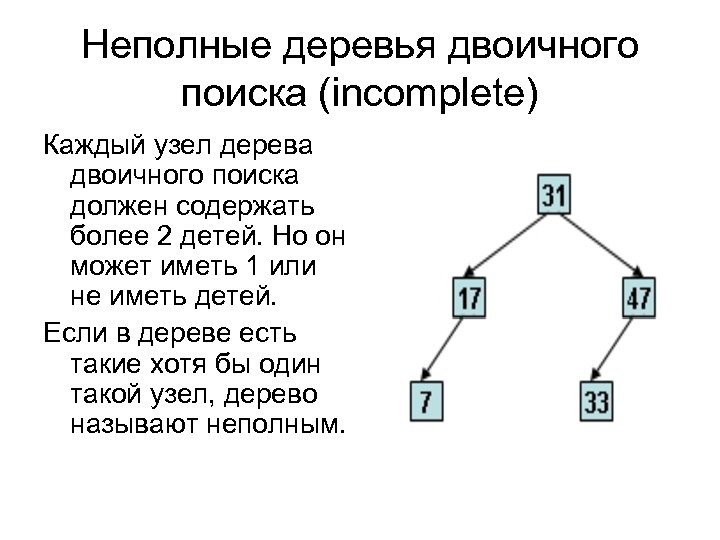Неполные деревья двоичного поиска (incomplete) Каждый узел дерева двоичного поиска должен содержать более 2 детей. Но он может иметь 1 или не иметь детей. Если в дереве есть такие хотя бы один такой узел, дерево называют неполным.

Использование деревьев двоичного поиска Дерево двоичного поиска может быть использовано для реализации таких абстракций, как множество, словарь (набор соответствий "ключ-значение"), очередь с приоритетами и так далее.

Использование деревьев двоичного поиска Далее рассмотрим контейнеры STL, основанные на деревьях и приведем примеры работы с ними. Ассоциативные контейнеры обеспечивают быстрый доступ к данным за счет того, что они, как правило, построены на основе сбалансированных деревьев поиска.

Использование деревьев двоичного поиска Пояснения на следующем слайде

Использование деревьев двоичного поиска Поиск значений в двоичном дереве поиска реализован рекурсивно. Процедура принимает на вход вершину. Сравнивает ее значение с искомым: в случае равенства, искомое значение найдено, иначе – рекурсивно перемещаемся в корень соответствующего поддерева: либо большего, либо меньшего. Если же нужного поддерева нет, то искомое значение не содержится в дереве.

Использование STL Множество (set) – это ассоциативный контейнер, содержащий только значения ключей. • Значения ключей уникальны. Повторяющиеся элементы не заносятся в множество. • Элементы множества хранятся отсортированными

Работа со множествами • Объявление объектов класса set: • Добавление элементов во множество с помощью функции insert

Работа с множествами • Узнаем количество элементов множества с помощью функции size: • Поиск элемента множества, с помощью функции find:

Алгоритмы работы с множествами Ассоциативные контейнеры могут использоваться в сочетании c алгоритмами работы со множествами.

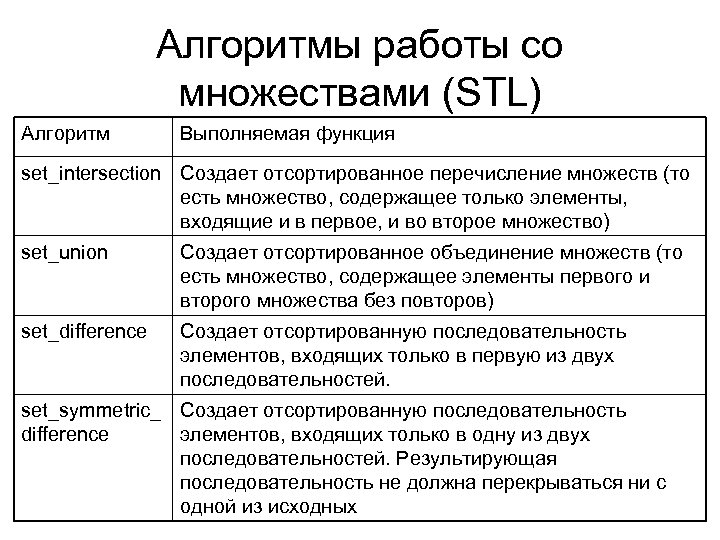Алгоритмы работы со множествами (STL) Алгоритм Выполняемая функция set_intersection Создает отсортированное перечисление множеств (то есть множество, содержащее только элементы, входящие и в первое, и во второе множество) set_union Создает отсортированное объединение множеств (то есть множество, содержащее элементы первого и второго множества без повторов) set_difference Создает отсортированную последовательность элементов, входящих только в первую из двух последовательностей. set_symmetric_ Создает отсортированную последовательность difference элементов, входящих только в одну из двух последовательностей. Результирующая последовательность не должна перекрываться ни с одной из исходных

Пример использования алгоритмов работы со множествами

Использование STL Словарь (map) Словарь map – это ассоциативный массив, построенный на основе пар значений: - ключ для идентификации элемента - собственно элемент • Значения ключей уникальны (кроме multimap) • Элементы в словаре хранятся отсортированными

Работа со словарем • Объявление объектов класса map: • Вставка элементов с помощью функции insert

Работа со словарем • Более быстрый способ вставки элемента с помощью операции [ ] : • Доступ к элементам по ключу с помощью операции [ ]: • Просмотр элеметов с помощью итератеров

Использование STL Очереди с приоритетами (priority_queue) В очереди с приоритетами каждому элементу соответствует приоритет, определяющий порядок выборки из очереди. По умолчанию он определяется с помощью операции <. То есть из очереди каждый раз выбирается максимальный элемент.

Пример использования очереди с приоритетами

Библиотека STL позволяет в качестве функций сравнения использовать пользовательские функции либо классы.

Использование контейнеров + : Использование контейнеров позволяет значительно повысить надежность программ, их переносимость и универсальность, а также уменьшить сроки их разработки. - : Снижение быстродействия в некоторых случаях может быть весьма значительным. Для эффективного использования необходимо затратить достаточно времени на освоение библиотеки.

Стандартные классы просто так в состав С++ не добавляются. • Г. Шилдт