Деревья Бинарные деревья Прошивка бинарных деревьев

Деревья. Бинарные деревья.

Прошивка бинарных деревьев ► замена по определенному правилу пустых указателей на сыновей указателями на последующие узлы, соответствующие обходу ►N ► ( N+1 ) NULL ► "нити"

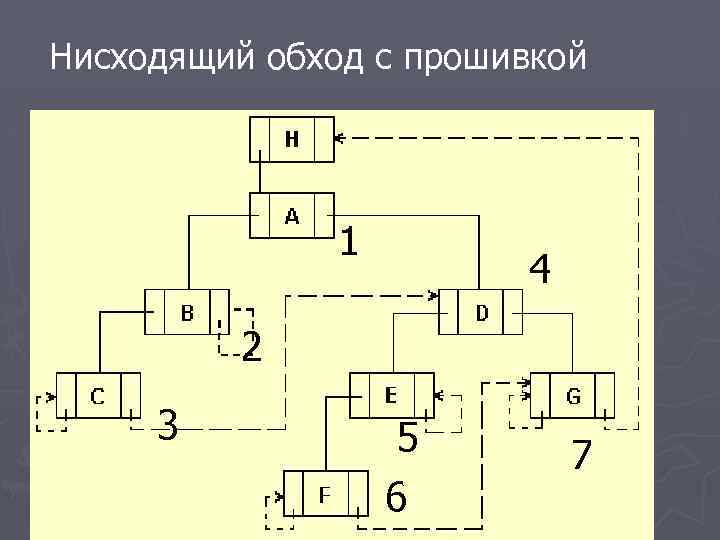
Нисходящий обход с прошивкой 1 4 2 3 5 6 7

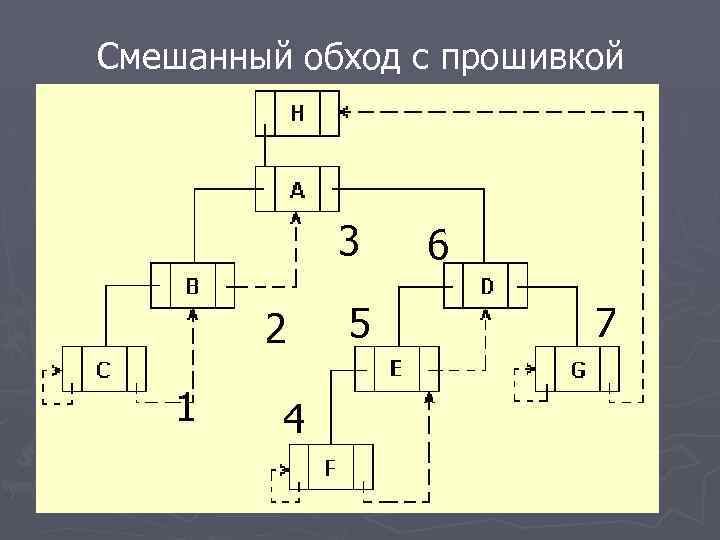
Смешанный обход с прошивкой 3 2 1 4 5 6 7

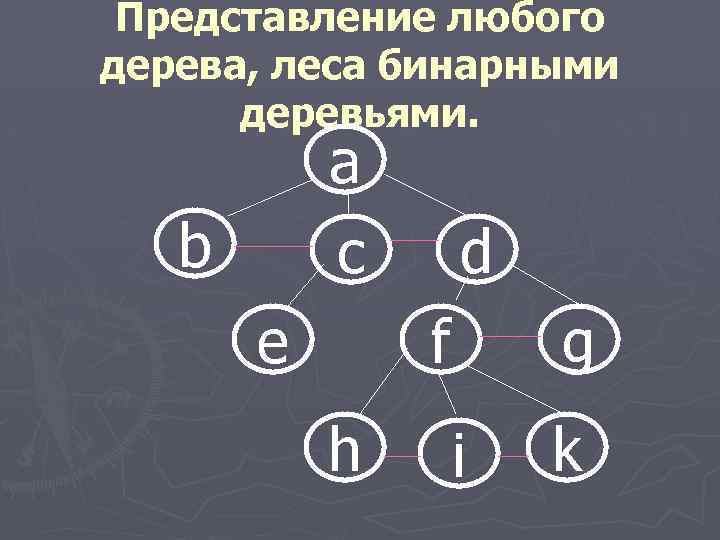
Представление любого дерева, леса бинарными деревьями. a b c e d f h g i k

алгоритм ►В каждом узле оставить только ветвь к старшему сыну; ► 2. Соединить горизонтальными ребрами всех братьев одного отца; ► 3 Развернуть дерево таким образом, чтобы все вертикальные ветви отображали левых сыновей, а горизонтальные - правых.

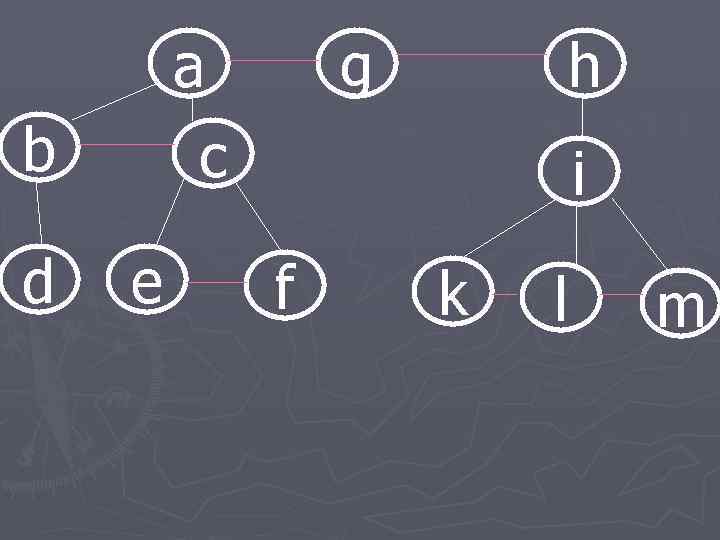
a b d g h c e i f k l m

алгоритм ► корни всех поддеревьев леса соединить горизонтальными связями. ► использовать алгоритм представления любого дерева бинарным деревом

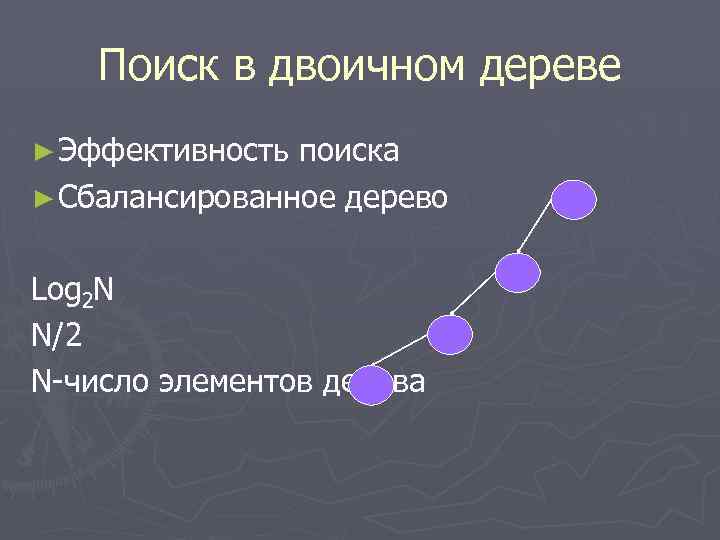
Поиск в двоичном дереве ► Эффективность поиска ► Сбалансированное дерево Log 2 N N/2 N-число элементов дерева

Сбалансированные деревья AVL-деревья Дерево является СБАЛАНСИРОВАННЫМ тогда и только тогда, когда для каждого узла высота его двух поддеревьев различается не более чем на 1. Адельсоном-Вельским и Ландисом АВЛ-дерево AVL-дерво

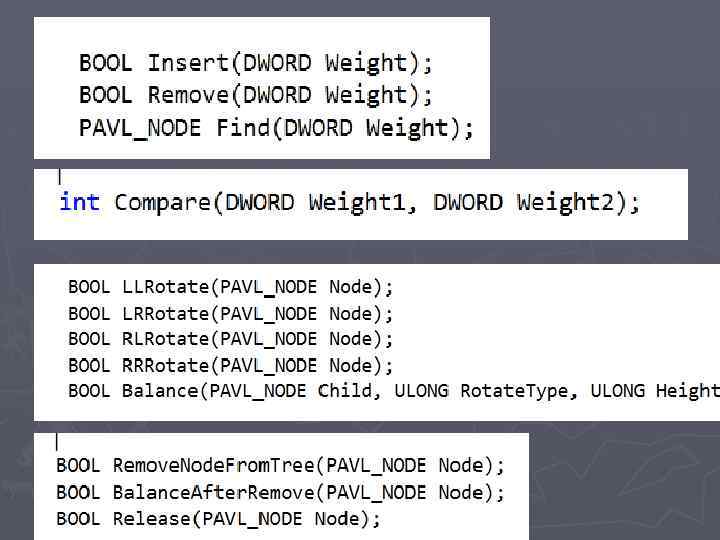
операции ► Вставить новый элемент ► Удалить заданный элемент ► Поиск заданного элемента

показатель сбалансированногсти (balance factor) ► Левое (L) - узел левоперевешивающий, если самый длинный путь по ее левому поддереву на единицу больше самого длинного пути по ее правому поддереву ► Сбалансированное (B) - равны наиболее длинные пути по обеим ее поддеревьям ► Правое (R) - узел правоперевешивающий, если самый длинный путь по ее правому поддереву на единицу больше самого длинного пути по ее левому поддереву

Включение ► 1. Следовать по пути поиска, пока не будет найден ключ или окажется, что ключа нет в дереве. ► 2. Включить новый узел и определить новый показатель сбалансированности. ► 3. Пройти обратно по пути поиска и проверить показатель сбалансированности у каждого узла. ► 4. Корректировать ссылки дерева.

виды балансировки ► однократный правый (RR) поворот ► однократный левый (LL) поворот ► двукратный поворот налево и направо (LR) ► двукратный поворот направо и налево (RL) ► число вращений не превышает С · h

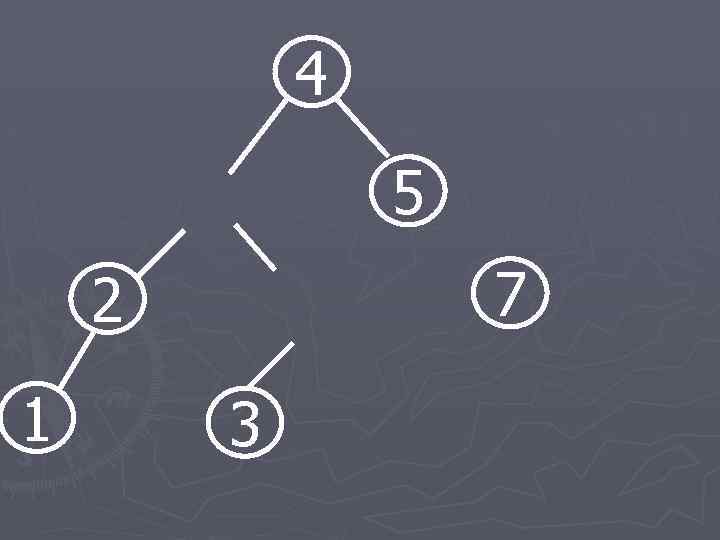
4 5 7 2 1 3

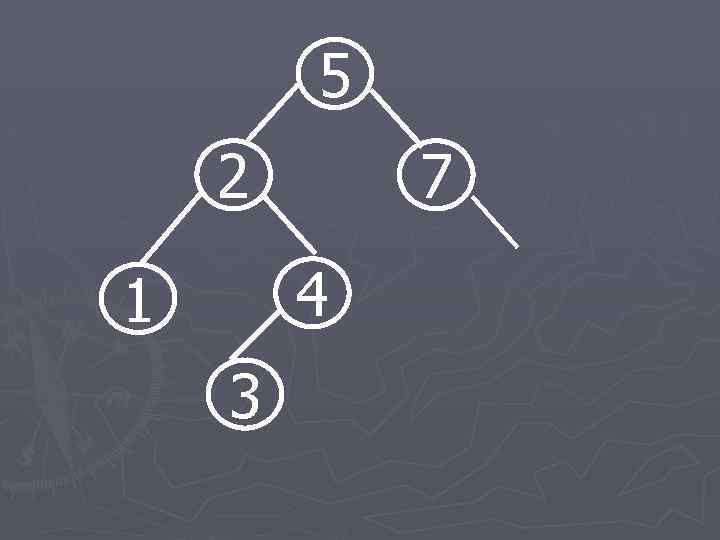
5 2 7 4 1 3

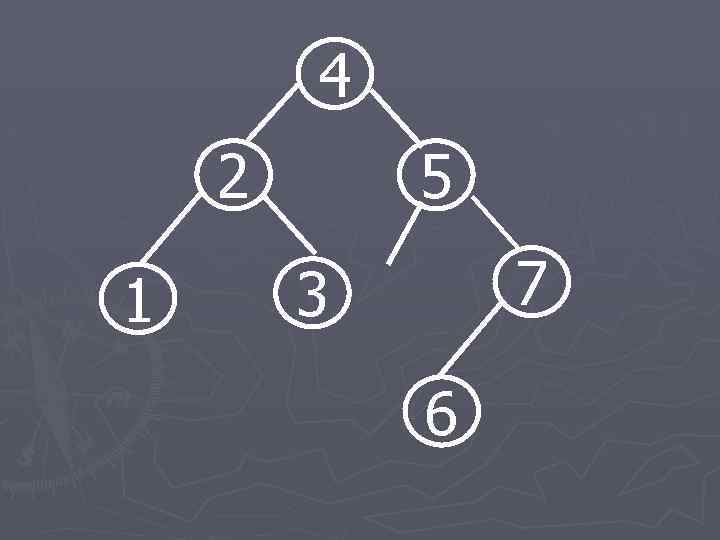
4 2 1 5 7 3 6

Удаление ► 1. Следовать по дереву, пока не будет найден удаляемый элемент. ► 2. Удалить найденный элемент, не разрушив структуры связей между элементами. ► 3. Произвести балансировку полученного дерева и откорректировать показатели сбалансированности.

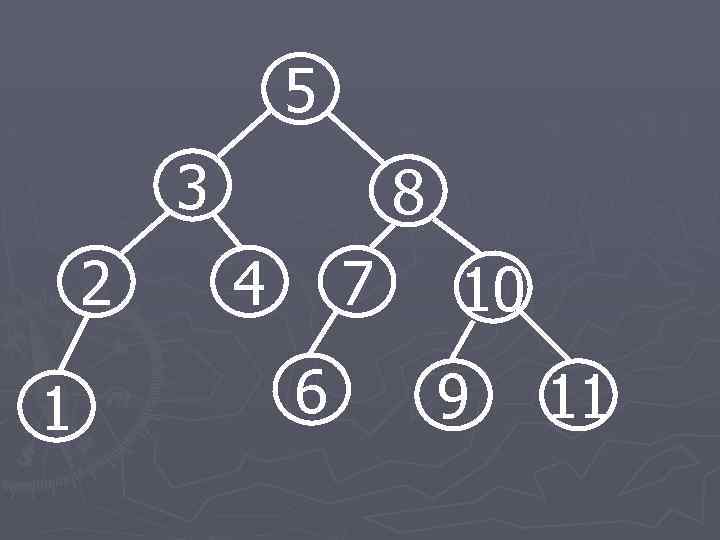
5 3 2 1 8 4 7 6 10 9 11

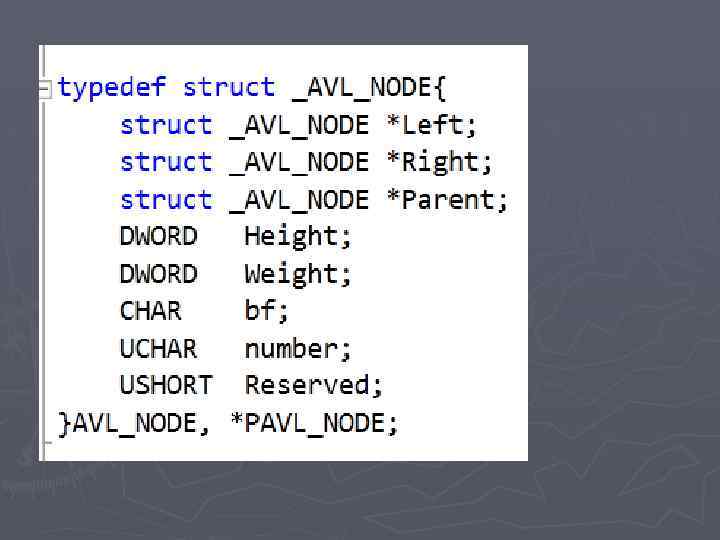
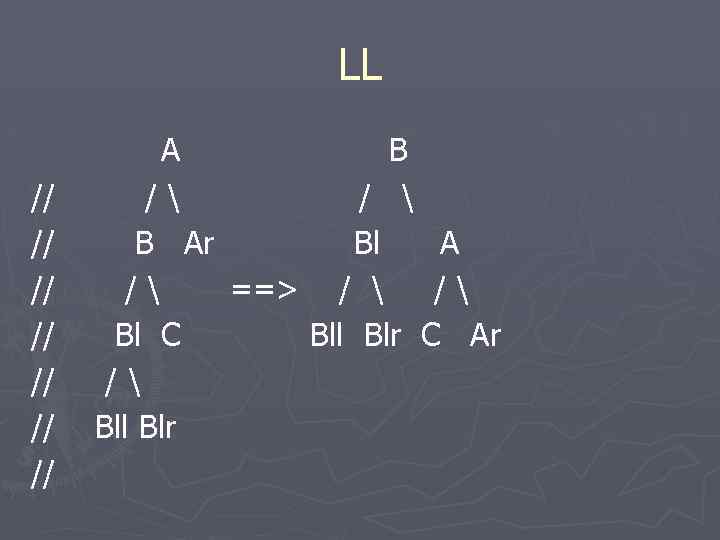
LL // // A B / / B Ar Bl A / ==> / / Bl C Bll Blr C Ar / Bll Blr

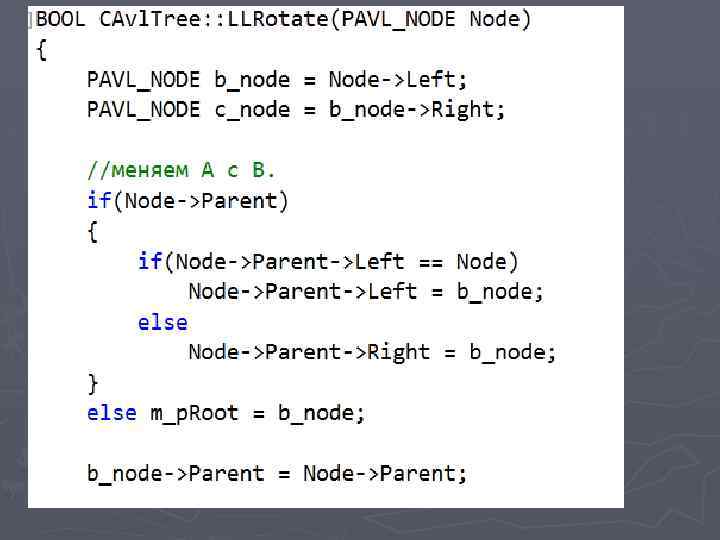
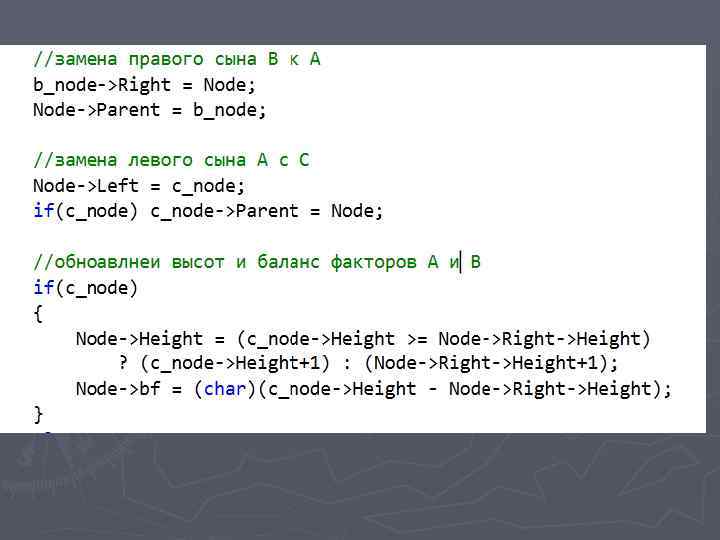
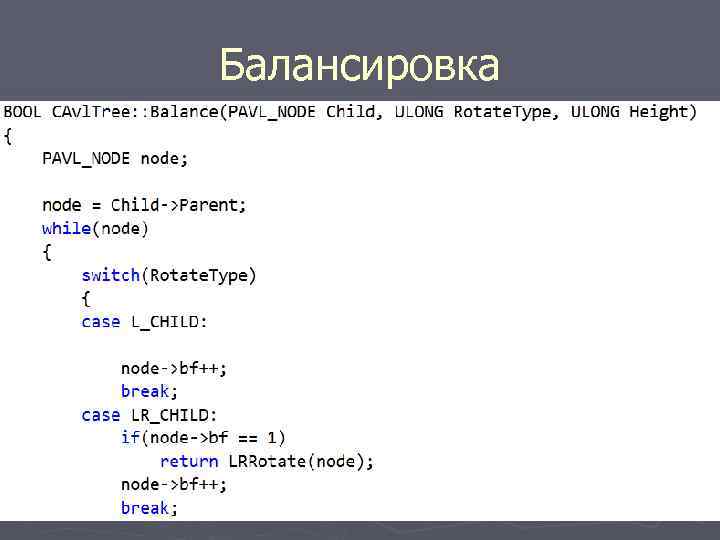
Балансировка

Балансировка через массив ► (1) Скопировать данные из дерева в массив в отсортированном виде (2) очистить дерево. (3) добавить элемент из массива не отсортировано; средний элемент – вершина и т. д. ; средний левой части, средний правой части и ► т. д. ►.

► Высота сбалансированного дерева h ► h <= log 2 n + 1 ► h <= C log 2 n

Красно-черные деревья ► RB-деревья ► Байером ► set в 1972 и map

RB- бинарное дерево со след свойствами ► каждая внешняя (или нулевая) вершина считается черной; ► корневая вершина дерева черная; ► у красной вершины дети черные; ► всякий путь от корня дерева к произвольной внешней вершине имеет одно и то же количество черных вершин (сбалансированность по черным).

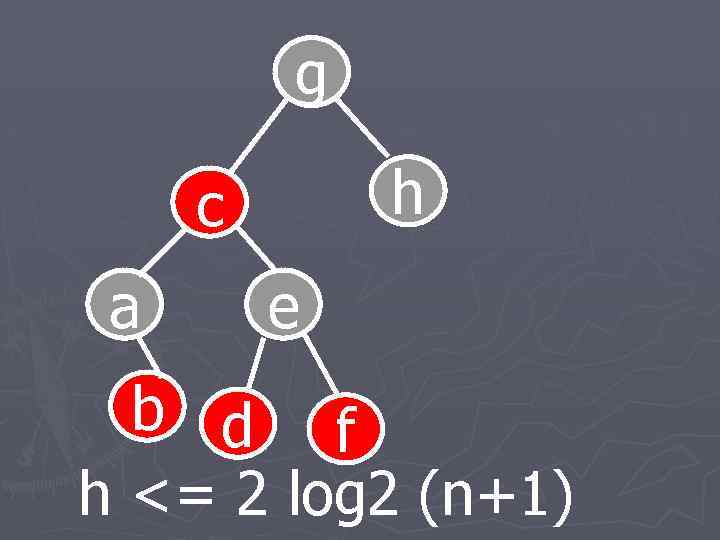
g h c a e b d f h <= 2 log 2 (n+1)

Преимущества RB ► Простая процедура восстановления сбалансированности ►перекраска § операции вращения вершины влево и вправо, (не больше двух при добавлении элемента и не больше четырех при удалении). § число операций при восстановлении структуры RB-дерева <= K · h

реализация

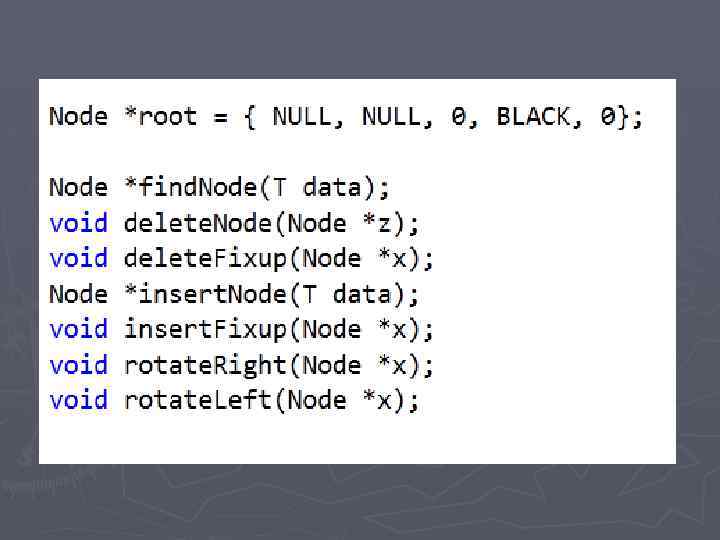
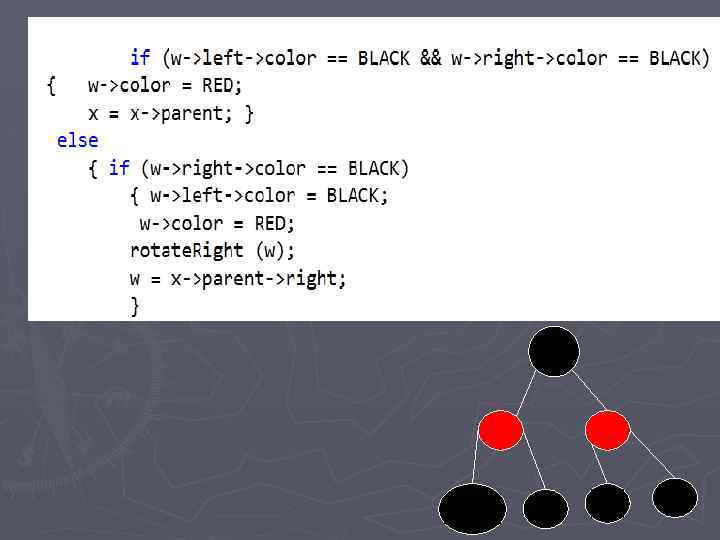
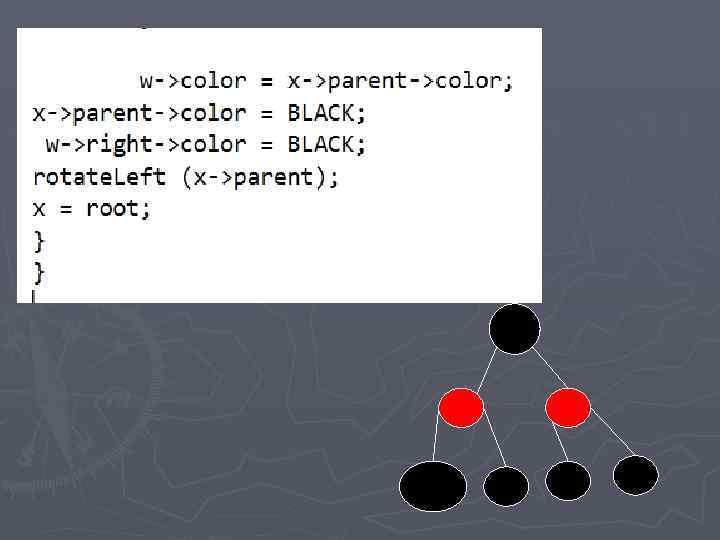
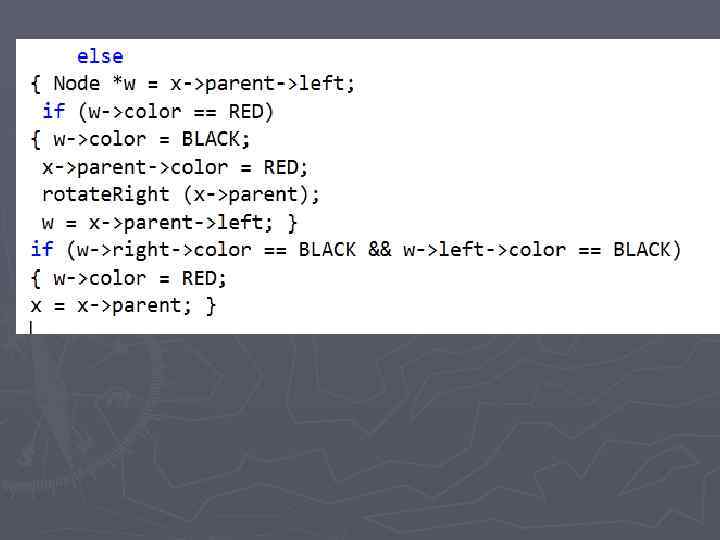
Приложения деревьев ► Трансляторы таблиц решений ► создание и ведение таблиц символов ► экономическое кодирование сообщений ► решение арифметических выражений

Алгоритм Хаффмана ►А В А С С D А ► А -3 раза, С -2 раза, В -1 раз, D -1 раз тоесть можно ► 1. использовать коды переменной длины. ► 2. код одного символа не должен совпадать с кодом другого (раскодирование идет слева направо). ► АВАССDА ► 0 10 0 110 111 0 -13 бит.

Алгоритм 1)прочтение полностью файла и подсчет встречаемости каждого символ из расширенного набора ASCII; 2)выстраивание исходных символов в соответствии с их вероятностями по убыванию (сортировка таблицы ссылок не меняя местонахождение каждого символа; каждую ссылку из последней таблицы назовем "узлом");

► 3)объединение двух последних символов в композицию символов, с частотой вхождения равной сумме частот; ► 4)повторение шага 2 до тех пор, пока не получится композиция с частотой равной размеру файла (называемая корнем). Полученная структура называется деревом Хаффмана; ► ► 5)трассировка от корня до соответствующего символа и присвоение 0 левой и 1 правой ветви.

. Пусть имеется файл длинной 100 байт и имеющий 6 различных символов в себе. Подсчитываем вхождение каждого из символов в файл и получили следующее : Таблица 1 Символ A B C D E F Частота 10 20 30 5 25 10 вхождений

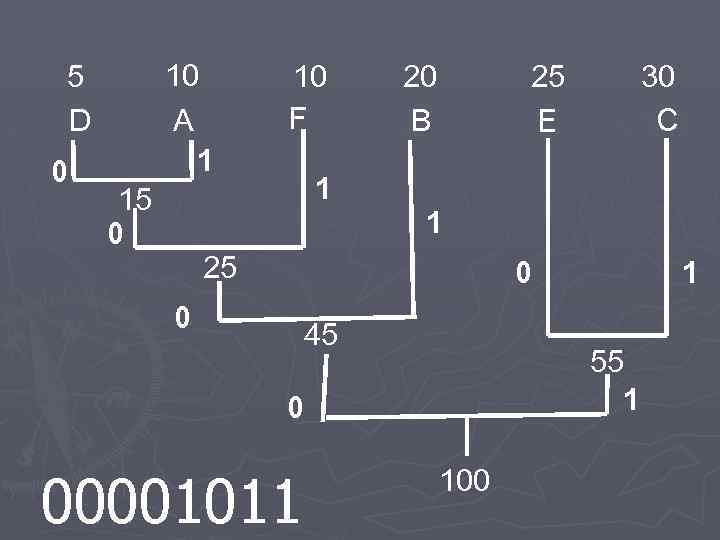
10 A 1 5 D 0 15 0 10 F 1 20 B 25 E 30 C 1 25 0 0 45 55 1 0 00001011 1 100

Таблица 2 Символ Размер (бит) B E 11 0000 001 01 10 2 Код С A 2 2 4 D 4 F 3

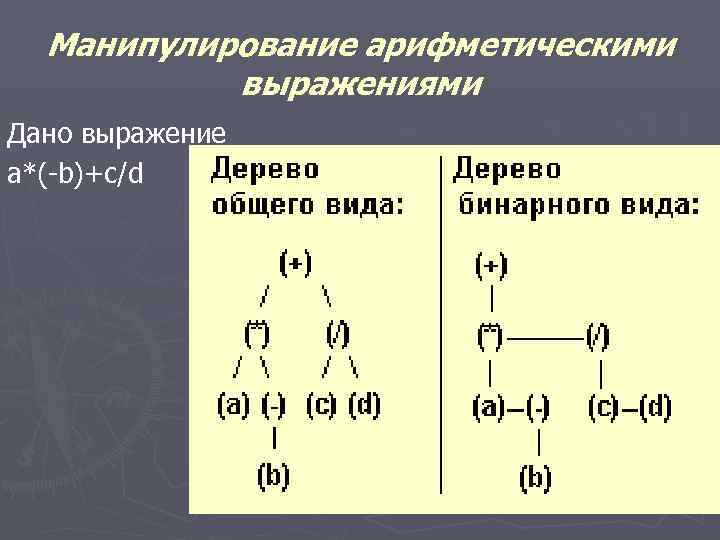
Манипулирование арифметическими выражениями Дано выражение а*(-b)+с/d

Формирование таблиц символов LPTR SYMBOLS INFO RPTR

► Длина пути – число ребер соединяющих вершины ► Глубина дерева – длина пути от корня до произвольной вершины ► Высота дерева – максимальная глубина вершины ► Если N число вершин, то высота дерева h=log 2 N