Дерево решений как инструмент визуализации принятии решений в

Дерево решений как инструмент визуализации принятии решений в условиях неопределенности ПРИМЕР Кафедра ВТ Казанская О. В. 1

ОПРЕДЕЛЕНИЕ • Дерево – конечный связный граф, состоящий по крайней мере из двух вершин и не содержащий циклов 2

Пример инвестиционного проекта Известно: • Некоторая компания предполагает построить новое предприятие. Имеется несколько вариантов развития (срок планирования 10 лет) • 1 ВАРИАНТ – строительство большого предприятия. Стоимость - $ 3 млн Предполагаемый доход в разных ситуациях: а) высокий спрос с доходом $ 1 млн в год б) высокий спрос первые 2 года (с доходом $ 1 млн в год), затем снижение спроса с доходом $ 100 тыс. в год в) низкий спрос все 10 лет с доходом $ 100 тыс. в год 3

ПРИМЕР 1: условия задачи «выбор инвестиционного проекта» Известно: • 2 ВАРИАНТ – строительство небольшого предприятия. Стоимость - $ 1, 3 млн Предполагаемый доход в разных ситуациях: а) высокий спрос первые 2 года с доходом $ 450 тыс. в год; затем дилемма: А) расширение предприятия (затраты $ 2, 2 млн) ; возможные варианты развития: Аа) высокий спрос 8 лет, доход - $ 700 тыс. в год Аb) низкий спрос, доход - $ 50 тыс. б) низкий спрос первые 2 года с доходом $ 40 тыс. в год – дальнейшее расширение нецелесообразно 4

ПРИМЕР 1: условия задачи «выбор инвестиционного проекта» Известно: • 2 ВАРИАНТ – строительство небольшого предприятия. Стоимость - $ 1, 3 млн Предполагаемый доход в разных ситуациях: а) высокий спрос первые 2 года с доходом $ 450 тыс. в год; затем дилемма: B) предприятие не расширяется (затрат нет) , возможные варианты развития: Bа) высокий спрос 8 лет, доход - $ 300 тыс. в год Bb) низкий спрос 8 лет, доход - $ 40 тыс. в год 5

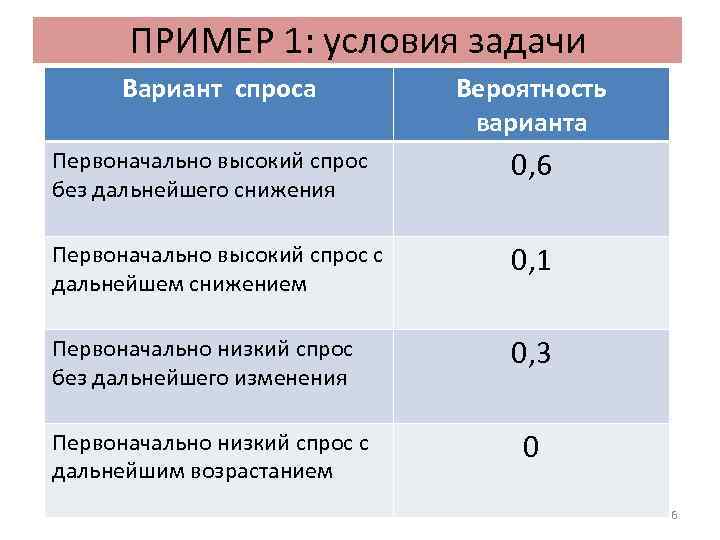ПРИМЕР 1: условия задачи Вариант спроса Известно: Вероятность варианта Первоначально высокий спрос без дальнейшего снижения 0, 6 Первоначально высокий спрос с дальнейшем снижением 0, 1 Первоначально низкий спрос без дальнейшего изменения 0, 3 Первоначально низкий спрос с дальнейшим возрастанием 0 6

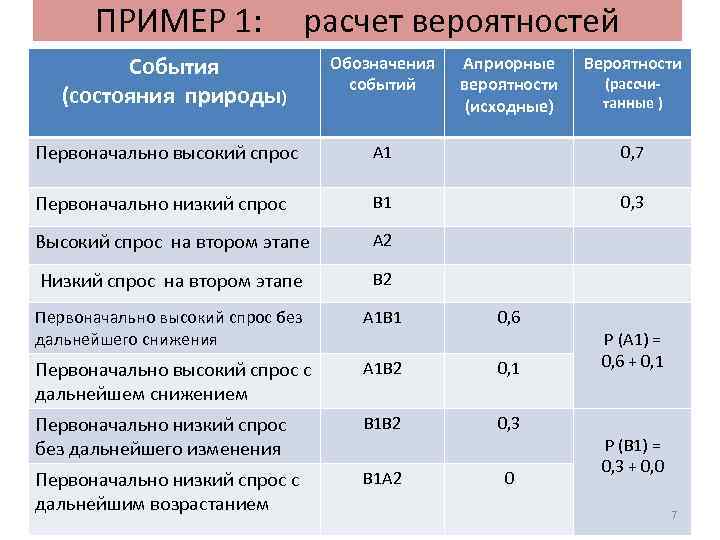ПРИМЕР 1: расчет вероятностей События (состояния природы) Обозначения событий Априорные вероятности (исходные) Вероятности (рассчитанные ) Первоначально высокий спрос А 1 0, 7 Первоначально низкий спрос B 1 0, 3 Высокий спрос на втором этапе А 2 Низкий спрос на втором этапе B 2 Первоначально высокий спрос без дальнейшего снижения А 1 B 1 0, 6 Первоначально высокий спрос с дальнейшем снижением А 1 B 2 0, 1 Первоначально низкий спрос без дальнейшего изменения B 1 B 2 0, 3 Первоначально низкий спрос с дальнейшим возрастанием B 1 A 2 0 P (A 1) = 0, 6 + 0, 1 P (B 1) = 0, 3 + 0, 0 7

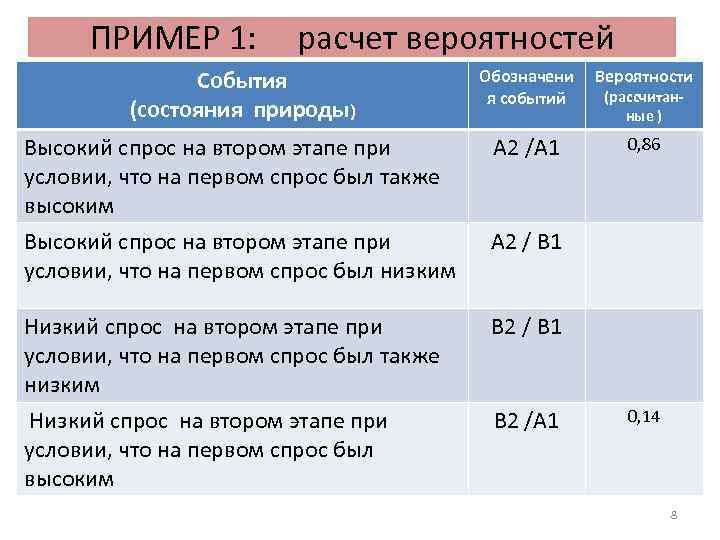ПРИМЕР 1: расчет вероятностей События (состояния природы) Обозначени я событий Вероятности Высокий спрос на втором этапе при условии, что на первом спрос был также высоким A 2 /А 1 0, 86 Высокий спрос на втором этапе при условии, что на первом спрос был низким A 2 / B 1 Низкий спрос на втором этапе при условии, что на первом спрос был также низким Низкий спрос на втором этапе при условии, что на первом спрос был высоким B 2 / B 1 B 2 /А 1 (рассчитанные ) 0, 14 8

ПРИМЕР 1: расчет вероятностей Теорема умножения вероятностей: P (A*B) = P (A) * P (B / A) Т. е. : P (A 1*A 2) = P (A 1) * P (A 2 / A 1) или Р (А 2 / А 1) = P (A 1*A 2) / P (A 1) = 0, 6 / 0, 7 = 0, 86 Р (B 2 / А 1) = P (A 1*B 2) / P (A 1) = 0, 1 / 0, 7 = 0, 14 Р (А 2 / А 1) + Р (B 2 / А 1) = 1, 0 !! 9

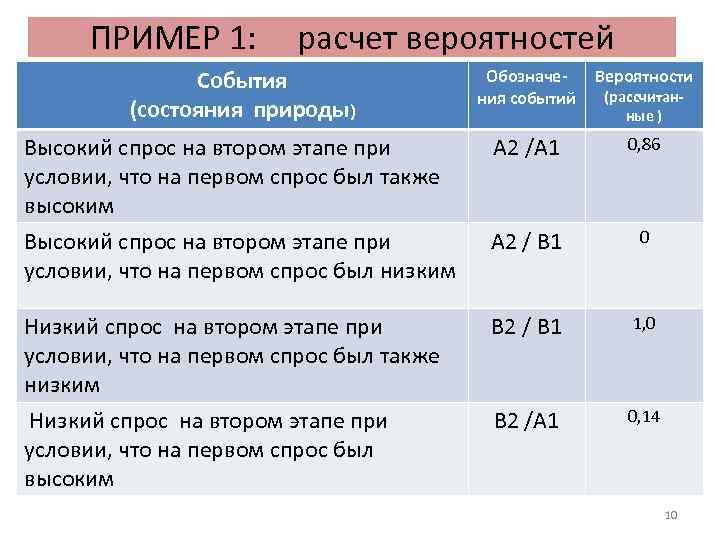ПРИМЕР 1: расчет вероятностей События (состояния природы) Обозначения событий Вероятности Высокий спрос на втором этапе при условии, что на первом спрос был также высоким A 2 /А 1 0, 86 Высокий спрос на втором этапе при условии, что на первом спрос был низким A 2 / B 1 0 Низкий спрос на втором этапе при условии, что на первом спрос был также низким Низкий спрос на втором этапе при условии, что на первом спрос был высоким B 2 / B 1 1, 0 B 2 /А 1 0, 14 (рассчитанные ) 10

ПРИМЕР 1: расчет вероятностей Теорема умножения вероятностей: P (A*B) = P (A) * P (B / A) Т. е. : P (B 1*B 2) = P (B 1) * P (B 2 / B 1) или Р (B 2 / B 1) = P (B 1*B 2) / P (B 1) = 0, 3 / 0, 3 = 1, 0 Р (B 2 / А 1) = P (A 1*B 2) / P (A 1) = 0, 0 / 0, 3 = 0, 0 Р (B 2 / B 1) + Р (B 2 / А 1) = 1, 0 !! 11

ПРИМЕР 1: искомые решения d 1 d 21 d 22 вложения в крупный завод (затраты $ 3 млн) вложения в небольшой завод (затраты $ 1, 3 млн) расширение малого предприятия (затраты $ 2, 2 млн) отказ от дальнейшего развития предприятия 12

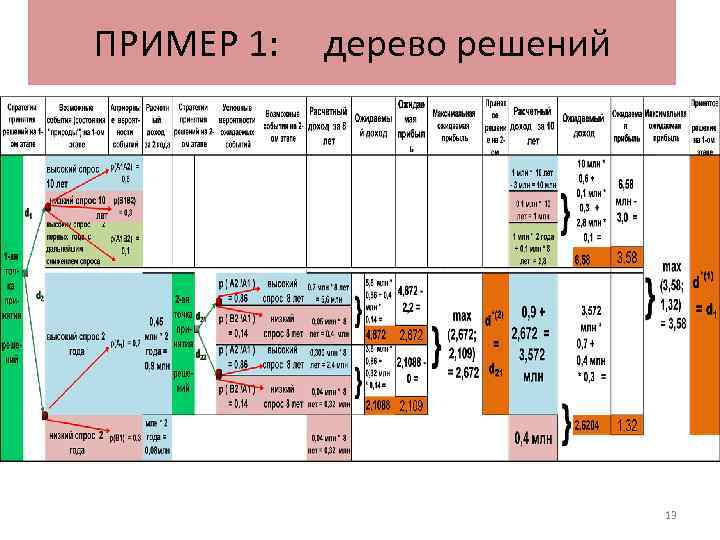ПРИМЕР 1: дерево решений 13

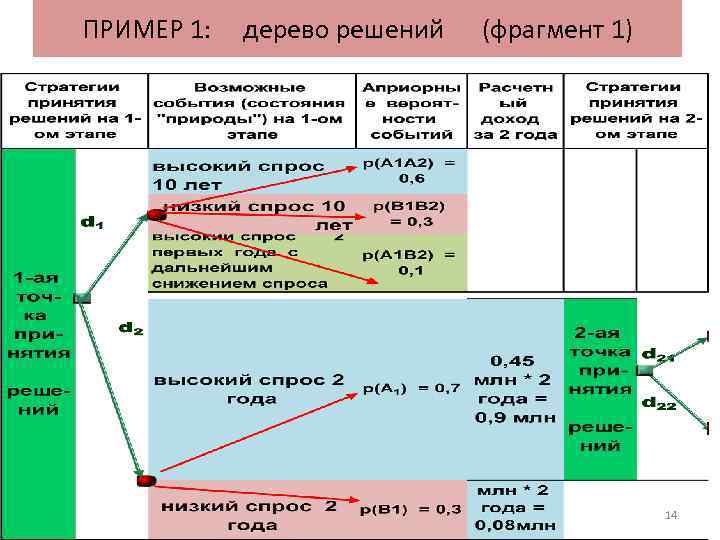ПРИМЕР 1: дерево решений (фрагмент 1) 14

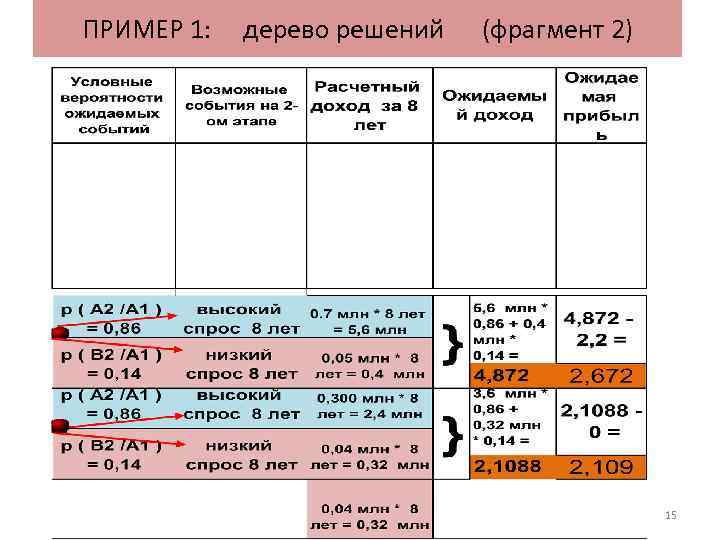ПРИМЕР 1: дерево решений (фрагмент 2) 15

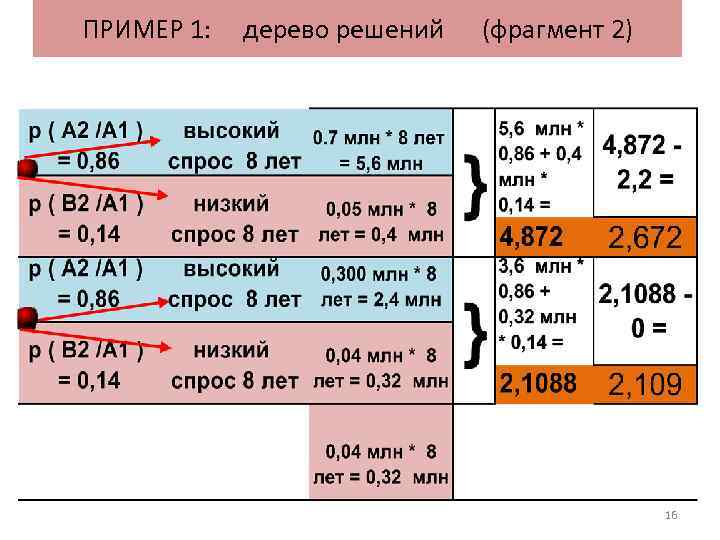ПРИМЕР 1: дерево решений (фрагмент 2) 16

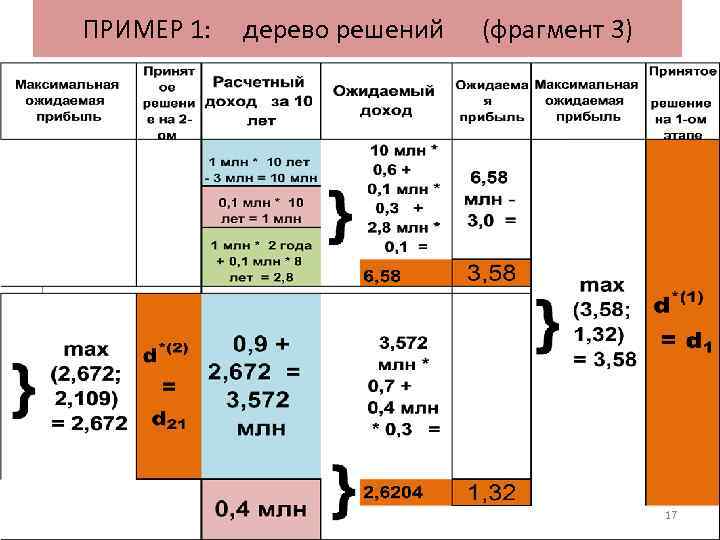ПРИМЕР 1: дерево решений (фрагмент 3) 17