Dependent Types for Termination Verification Hongwei Xi University

Dependent Types for Termination Verification Hongwei Xi University of Cincinnati 1

Overview Motivation n n Program error detection at compile-time Compilation certification Termination Verification for Dependent ML n n Theoretical development Practical applications Conclusion 2

Program Error Detection Unfortunately one often pays a price for [languages which impose no disciplines of types] in the time taken to find rather inscrutable bugs — anyone who mistakenly applies CDR to an atom in LISP and finds himself absurdly adding a property list to an integer, will know the symptoms. -- Robin Milner A Theory of Type Polymorphism in Programming Therefore, a stronger type discipline allows for capturing more program errors at compile-time. 3

Some Advantages of Types Detecting program errors at compile-time Enabling compiler optimizations Facilitating program verification n n Using types to encode program properties Verifying the encoded properties through typechecking Serving as program documentation n Unlike informal comments, types are formally verified and can thus be fully trusted 4

Compiler Correctness How can we prove the correctness of a (realistic) compiler? Source program e n n compilation Target code |. | |e | Verifying that the semantics of e is the same as the semantics of |e| for every program e But this simply seems too challenging (and is unlikely to be feasible) 5

Compilation Certification Source program e: P(e) holds compilation |. | Target code |e|: P(|e|) holds Assume that P(e) holds, i. e. , e has the property P Then P(|e|) should hold, too A compiler can be designed to produce a certificate to assert that |e| does have the property P 6

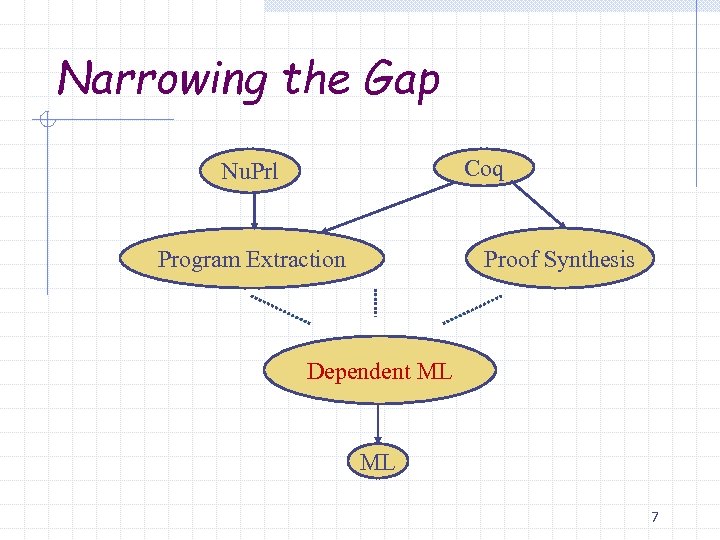Narrowing the Gap Coq Nu. Prl Program Extraction Proof Synthesis Dependent ML ML 7

Termination Verification Termination n is a liveness property can not be verified at run-time is often proven with a well-founded metric that decreases whenever a recursive function call is made 8

Primitive Recursion datatype Nat with nat = Z(0) | {n: nat} S(n+1) of Nat(n) (* Z: Nat(0) S: {n: nat} Nat(n) -> Nat(n+1) *) fun (‘a) R Z u v = u | R (S n) u v = v n (R n u v) withtype {n: nat} => Nat(n) -> ‘a -> (Nat -> ‘a) -> ‘a (* Nat is for [n: nat] Nat(n) *) 9

Ackermann Function in DML fun ack (m, n) = if m = 0 then n+1 else if n = 0 then ack (m-1, 1) else ack (m-1, ack (m, n-1)) withtype {m: nat, n: nat} => int(m) * int(n) -> nat (* Note: nat = [a: int | a >=0] int(a) *) 10

What’s really new here? We present a formalism that n n allows the programmer to supply crucial information for facilitating program termination verification can smoothly integrate into a realistic programming language 11

ML 0: start point base types d : : = int | bool | (user defined datatypes) types t : : = d | t 1 t 2 | t 1 * t 2 patterns p : : = x | c(p) | <> |

match clauses ms : : = (p e) | (p e | ms) expressions e : : = x | f | c | if (e, e 1, e 2) | <> | | lam x: t. e | fix f: t. e | e 1(e 2) | let x=e 1 in e 2 end | case e of ms values v : : = x | c | | lam x: t. e context G : : =. | G, x: t 12

Integer Constraint Domain We use a for index variables index expressions i, j : : = a | c | i + j | i – j | i * j | i / j | … index propositions P, Q : : = i < j | i <= j | i >= j | i <> j | P Q|P Q index sorts g : : = int | {a : g | P } index variable contexts f : : =. | f, a: g | f, P index constraints F : : = P | P F | a: g. F 13

Dependent Types dependent types t : : =. . . | d(i) | Pa: g. t | Sa: g. t For instance, int(0), bool array(16); nat = [a: int | a >= 0] int(a); {a: int | a >= 0} int list(a) -> int list(a) 14

DML 0: ML 0 + dependent types expressions e : : =. . . | la: g. v | e[i] | | open e 1 as in e 2 end values v : : =. . . | la: g. v | typing judgment f; G |- e: t 15