Скачать презентацию Демонстрационная курса Лекция 3 СЛОЖНЫЕ ПРОЦЕНТЫ Наращение Скачать презентацию Демонстрационная курса Лекция 3 СЛОЖНЫЕ ПРОЦЕНТЫ Наращение

L3.ppt

  • Количество слайдов: 41

Демонстрационная презентация курса Лекция 3 СЛОЖНЫЕ ПРОЦЕНТЫ. Наращение и дисконтирование Демонстрационная презентация курса Лекция 3 СЛОЖНЫЕ ПРОЦЕНТЫ. Наращение и дисконтирование

Начисление сложных годовых процентов n В средне- и долгосрочных финансово-кредитных операциях, если проценты не Начисление сложных годовых процентов n В средне- и долгосрочных финансово-кредитных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга, применяют сложные проценты. n База для начисления сложных процентов увеличивается с каждым шагом во времени. n Наращение по сложным процентам можно представить как последовательное реинвестирование средств, вложенных под простые проценты на один период начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, часто называют капитализацией процентов.

n Найдем формулу для расчета наращенной суммы при условии, что проценты начисляются и капитализируются n Найдем формулу для расчета наращенной суммы при условии, что проценты начисляются и капитализируются один раз в году (годовые проценты). n Для этого применяется сложная ставка наращения. n Обозначения: Р — первоначальный размер долга, n S — наращенная сумма на конец срока ссуды, n n — срок, число лет наращения, n i — уровень годовой ставки процентов. n

n В конце n-го года наращенная сумма будет равна (1) Проценты за этот же n В конце n-го года наращенная сумма будет равна (1) Проценты за этот же срок в целом (2) Проценты на проценты составляют (3)

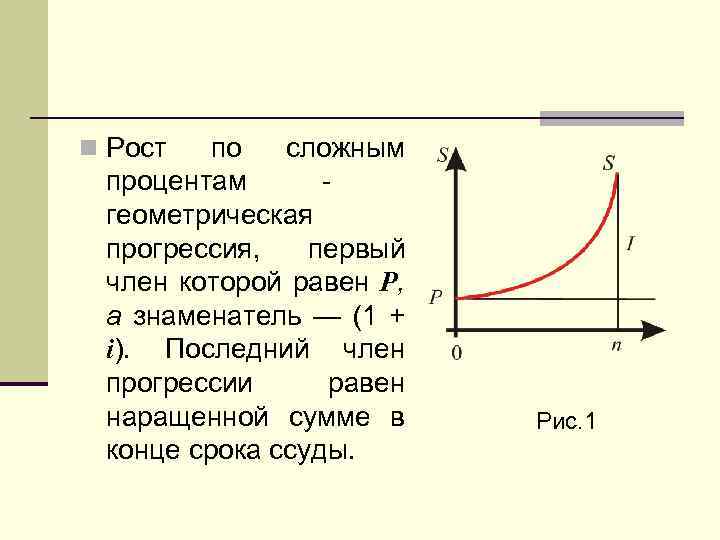n Рост по сложным процентам геометрическая прогрессия, первый член которой равен Р, а знаменатель n Рост по сложным процентам геометрическая прогрессия, первый член которой равен Р, а знаменатель — (1 + i). Последний член прогрессии равен наращенной сумме в конце срока ссуды. Рис. 1

n Множитель наращения сложных процентов за полный срок n периодов по процентной ставке i n Множитель наращения сложных процентов за полный срок n периодов по процентной ставке i за каждый, является основным финансовым коэффициентом и показывает будущую стоимость 1 денежной единицы, вложенной на n периодов под сложные проценты, начисляемые в по ставке i.

n Формула наращения по сложным процентам (1) получена для годовой процентной ставки и срока, n Формула наращения по сложным процентам (1) получена для годовой процентной ставки и срока, измеряемого в годах. n Однако ее можно применять и при других периодах начисления. В этих случаях i означает ставку за один период начисления (месяц, квартал и т. д. ), а n — число таких периодов.

Замечание Формулы (1)—(3) предполагают, что проценты начисляются по той же ставке, что и при Замечание Формулы (1)—(3) предполагают, что проценты начисляются по той же ставке, что и при начислении на основную сумму долга.

Пусть проценты на основной долг начисляются по ставке i, а проценты на проценты — Пусть проценты на основной долг начисляются по ставке i, а проценты на проценты — по ставке r ≠ i. В этом случае (4)

Начисление процентов в смежных календарных периодах Выше при начислении процентов не принималось во внимание Начисление процентов в смежных календарных периодах Выше при начислении процентов не принималось во внимание расположение срока начисления процентов относительно календарных периодов. Однако, часто даты начала и окончания ссуды находятся в разных периодах. Ясно, что начисленные за весь срок проценты не могут быть отнесены только к последнему периоду. В этом случае возникает задача распределения начисленных процентов по периодам.

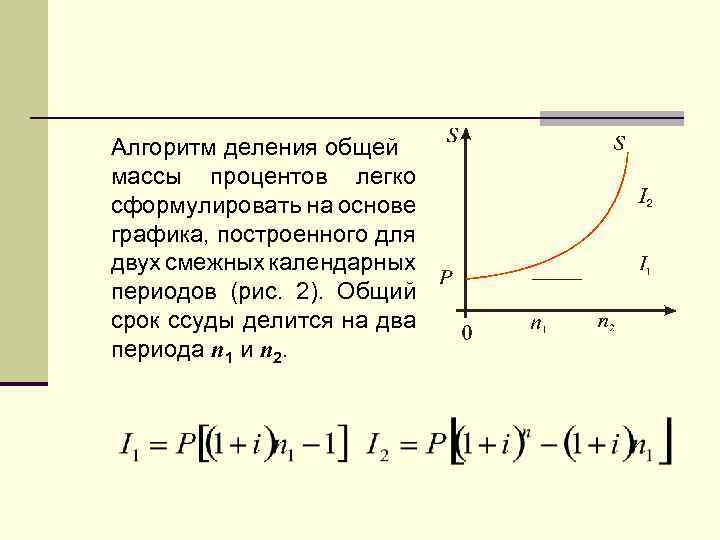Алгоритм деления общей массы процентов легко сформулировать на основе графика, построенного для двух смежных Алгоритм деления общей массы процентов легко сформулировать на основе графика, построенного для двух смежных календарных периодов (рис. 2). Общий срок ссуды делится на два периода n 1 и n 2.

Переменные ставки n Формула (1) предполагает постоянную ставку на протяжении всего срока начисления процентов. Переменные ставки n Формула (1) предполагает постоянную ставку на протяжении всего срока начисления процентов. Неустойчивость кредитно-денежного рынка диктует применение плавающих ставок. n В этом случае, общий множитель наращения определяется как произведение частных, т. е. (5) i 1, i 2, . . ik - последовательные значения ставок; n 1, n 2, . . nk - периоды, в течение которых "работают" соответствующие ставки.

Начисление процентов при дробном числе лет Часто срок в годах для начисления процентов не Начисление процентов при дробном числе лет Часто срок в годах для начисления процентов не является целым числом. В правилах ряда коммерческих банков для некоторых операций проценты начисляются только за целое число лет или других периодов начисления. Дробная часть периода отбрасывается. В большинстве же случаев учитывается полный срок. При, этом применяют два метода.

n Общий метод: расчет ведется непосредственно по формуле (1). n Смешанный метод предполагает начисление n Общий метод: расчет ведется непосредственно по формуле (1). n Смешанный метод предполагает начисление процентов за целое число лет по формуле сложных процентов и за дробную часть срока по формуле простых процентов: n (6) n = a + b – срок ссуды, a – целое число лет, b – дробная часть года. n Аналогичный метод применяется и в случаях, когда периодом начисления является полугодие, квартал или месяц.

Наращение процентов т раз в году n В современных условиях в связи с развитием Наращение процентов т раз в году n В современных условиях в связи с развитием систем электронных платежей проценты могут начисляться даже чаще, чем один раз в день. Пусть годовая ставка равна j, число периодов начисления в году - т. Каждый раз проценты начисляются по ставке j/т. Ставку j называют номинальной. Формулу наращения имеет вид: n (7) где N — общее количество периодов начисления.

n При более частом, чем один раз в год, начислении сложных процентов внутри года, n При более частом, чем один раз в год, начислении сложных процентов внутри года, размер номинальной годовой ставки j пропорционально уменьшают, а длину срока в процентных периодах увеличивают во столько же раз. n В случае ежемесячной капитализации (m = 12) календарный срок 2 года выражается числом расчетных периодов 2·12=24 месяца, а ежемесячная процентная ставка получается из номинальной годовой делением на 12. Ясно, что при одинаковой номинальной годовой ставке j увеличение частоты начисления сложных процентов m приводит в конце каждого года к большему финансовому результату в виде будущей стоимости S.

n Эффективная ставка процента - эта ставка, которая измеряет реальный относительный доход, который получают n Эффективная ставка процента - эта ставка, которая измеряет реальный относительный доход, который получают в целом за год, т. е. эффективная ставка — это годовая ставка сложных процентов, которая дает тот же результат, что и m-разовое начисление процентов по ставке j / m. n Эффективная доходность вложений является инструментом приведения условий финансовых контрактов к сопоставимому виду.

n Обозначим эффективную ставку через i. По определению множители наращения по двум ставкам (эффективной n Обозначим эффективную ставку через i. По определению множители наращения по двум ставкам (эффективной и номинальной при mразовом начислении) должны быть равны другу: (8) (9)

Дисконтирование по сложной ставке n Если требуется определить Р по значению S по сложной Дисконтирование по сложной ставке n Если требуется определить Р по значению S по сложной ставке процентов, то на основе (1) получим (10) n Величину v называют дисконтным, учетным, или дисконтирующим множителем.

n Для случаев, когда проценты начисляются т раз в году, получим (11) Замечание. Величину n Для случаев, когда проценты начисляются т раз в году, получим (11) Замечание. Величину Р, полученную дисконтированием S называют современной текущей стоимостью или современен величиной S. Современная стоимость может быть рассчитана на любой момент до выплаты суммы S.

Разность S - P, в случае, когда P определено дисконтированием, называют дисконтом и обозначают Разность S - P, в случае, когда P определено дисконтированием, называют дисконтом и обозначают D. (12)

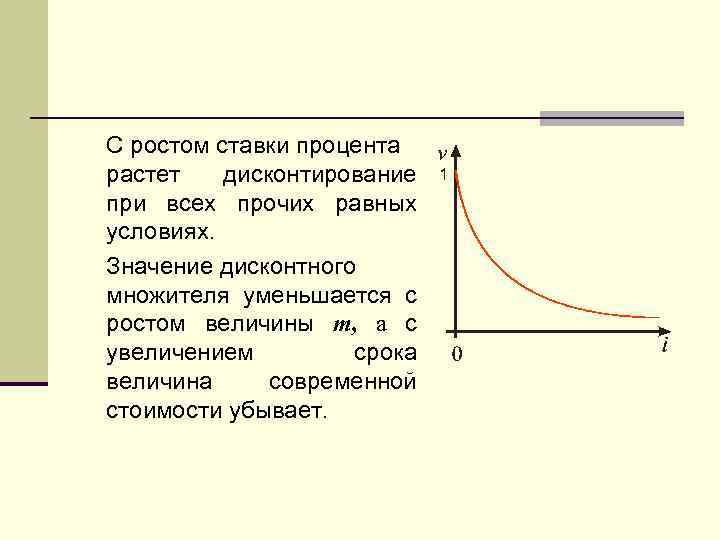С ростом ставки процента растет дисконтирование при всех прочих равных условиях. Значение дисконтного множителя С ростом ставки процента растет дисконтирование при всех прочих равных условиях. Значение дисконтного множителя уменьшается с ростом величины m, а с увеличением срока величина современной стоимости убывает.

Учет по сложной учетной ставке n. В практике учетных операций иногда применяют сложную учетную Учет по сложной учетной ставке n. В практике учетных операций иногда применяют сложную учетную ставку. В этих случаях процесс дисконтирования происходит с замедлением, так каждый раз учетная ставка применяется не к первоначальной сумме (как при простой учетной ставке), а к сумме, дисконтированной на предыдущем шаге во времени.

Дисконтирование по сложной учетной ставке осуществляется по формуле (13) d - сложная годовая учетная Дисконтирование по сложной учетной ставке осуществляется по формуле (13) d - сложная годовая учетная ставка.

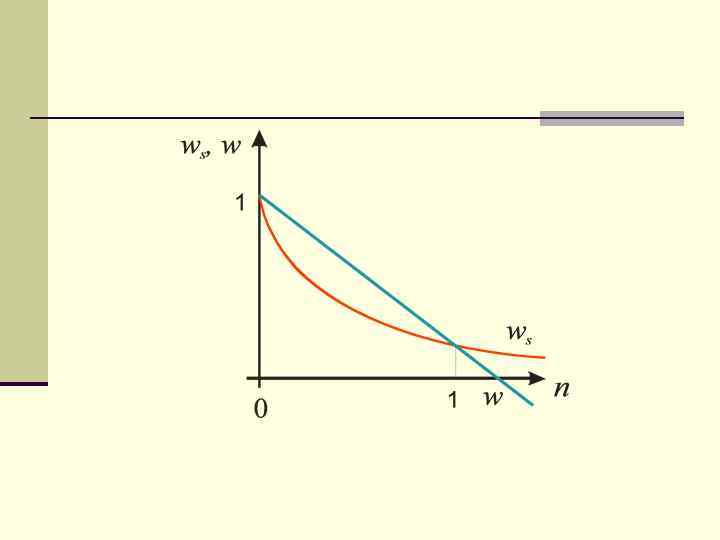
n Дисконтирование по сложной учетной ставке выгоднее для должника, чем по простой учетной ставке, n Дисконтирование по сложной учетной ставке выгоднее для должника, чем по простой учетной ставке, это видно при сравнении формул для дисконтных множителей: ds, d - простая и сложная учетные ставки соответственно.

n Дисконтирование по сложной учетной ставке выгоднее для должника, чем по простой учетной ставке, n Дисконтирование по сложной учетной ставке выгоднее для должника, чем по простой учетной ставке, это видно при сравнении формул для дисконтных множителей: Значение дисконтного множителя равномерно уменьшается по мере роста n и достигает нуля при n = 1/d.

n Дисконтирование по сложной учетной ставке выгоднее для должника, чем по простой учетной ставке, n Дисконтирование по сложной учетной ставке выгоднее для должника, чем по простой учетной ставке, это видно при сравнении формул для дисконтных множителей: Множитель экспоненциально уменьшается и достигает нуля лишь в пределе, при п = ∞.

Номинальная и эффективная учетные ставки Дисконтирование может производиться не один, а т раз в Номинальная и эффективная учетные ставки Дисконтирование может производиться не один, а т раз в году, т. е. каждый раз учет производится по ставке f / т , (14) f — номинальная годовая учетная ставка.

Эффективная учетная ставка d характеризует степень дисконтирования за год. Из равенства дисконтных множителей определим Эффективная учетная ставка d характеризует степень дисконтирования за год. Из равенства дисконтных множителей определим эффективную учетную ставку. Замечание. Эффективная учетная ставка во всех случаях, когда т > 1, меньше номинальной. (15) (16)

Наращение по сложной учетной ставке n Наращенную сумму можно получить используя сложную учетную ставку. Наращение по сложной учетной ставке n Наращенную сумму можно получить используя сложную учетную ставку. В этом случае имеем: (17) (18)

Срок ссуды n n При наращении по сложной годовойставке i и по номинальной ставке Срок ссуды n n При наращении по сложной годовойставке i и по номинальной ставке j имеем (19) (20)

Срок ссуды n n При дисконтировани и по сложной годовой учетной ставке d и Срок ссуды n n При дисконтировани и по сложной годовой учетной ставке d и по номинальной учетной ставке f получим (21) (22)

Величина процентной ставки n При наращении по сложной годовой ставке процентов i и по Величина процентной ставки n При наращении по сложной годовой ставке процентов i и по номинальной ставке j получим (23) (24)

При дисконтировании по сложным учетным ставкам dиf (25) (26) При дисконтировании по сложным учетным ставкам dиf (25) (26)

Непрерывное наращение и дисконтирование n В практических финансово-кредитных операциях непрерывное наращение применяется крайне редко, Непрерывное наращение и дисконтирование n В практических финансово-кредитных операциях непрерывное наращение применяется крайне редко, оно имеет значение в анализе сложных финансовых проблем, например при обосновании и выборе инвестиционных решений, в финансовом проектировании. n С помощью непрерывных процентов удается учесть сложные закономерности процесса наращения, например использовать изменяющиеся по определенному закону процентные ставки. n При непрерывном наращении процентов применяют особый вид процентной ставки — силу роста. Сила роста характеризует относительный прирост наращенной суммы за бесконечно малый промежуток времени. Она может быть постоянной или изменяться во времени.

Постоянная сила роста n При дискретном начислении процентов т раз в году по номинальной Постоянная сила роста n При дискретном начислении процентов т раз в году по номинальной ставке j наращенная

n Для того чтобы отличить непрерывную ставку от дискретной, обозначим силу роста как . n Для того чтобы отличить непрерывную ставку от дискретной, обозначим силу роста как . Тогда S=Pe n n При непрерывном наращении процентов наращенная сумма равна конечной величине, зависящей от первоначальной суммы, срока наращения и силы роста, которая в свою очередь представляет собой номинальную ставку сложных процентов при т .

n Дискретные и непрерывные ставки наращения находятся в функциональной зависимости: n Дискретные и непрерывные ставки наращения находятся в функциональной зависимости:

Переменная сила роста n Пусть сила роста изменяется во времени, следуя некоторому закону, представленному Переменная сила роста n Пусть сила роста изменяется во времени, следуя некоторому закону, представленному в виде непрерывной функции времени: t = f(t). Тогда наращенная сумма и современная величина определяются как

n Функция времени может быть самого различного вида, например линейная. В этом случае имеем n Функция времени может быть самого различного вида, например линейная. В этом случае имеем Здесь - начальное значение силы роста, а - прирост силы роста в единицу времени, q - множитель наращения.