Демонстрационная презентация курса Лекция 2 СЛОЖНЫЕ ПРОЦЕНТЫ Наращение

Демонстрационная презентация курса Лекция 2 СЛОЖНЫЕ ПРОЦЕНТЫ. Наращение и дисконтирование

Начисление сложных годовых процентов n В средне- и долгосрочных финансово- кредитных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга. n База для начисления сложных процентов увеличивается времени. с каждым шагом во

n В конце n-го года наращенная сумма будет равна Проценты за этот же срок в целом Проценты на проценты составляют

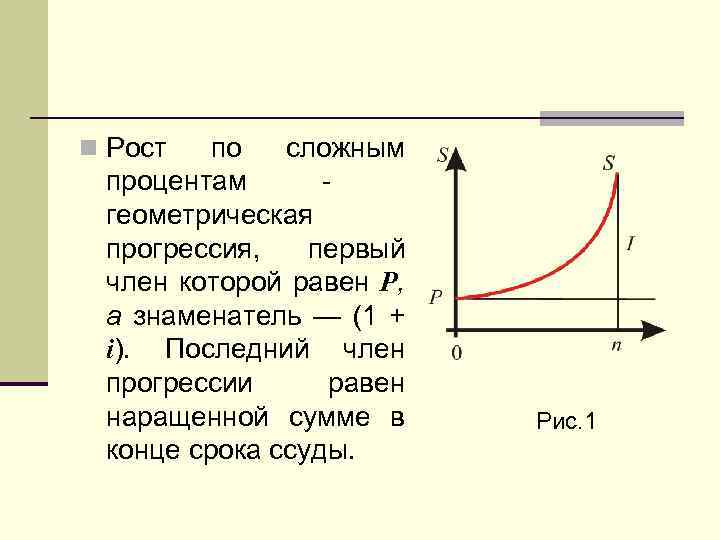n Рост по сложным процентам геометрическая прогрессия, первый член которой равен Р, а знаменатель — (1 + i). Последний член прогрессии равен наращенной сумме в конце срока ссуды. Рис. 1

Пусть проценты на основной долг начисляются по ставке i, а проценты на проценты — по ставке r ≠ i. В этом случае

Переменные ставки n Неустойчивость кредитно-денежного рынка диктует применение плавающих ставок. n В этом случае, общий множитель наращения определяется как произведение частных, т. е. i 1, i 2, . . ik - последовательные значения ставок; n 1, n 2, . . nk - периоды, в течение которых "работают" соответствующие ставки.

n Общий метод: расчет ведется непосредственно по формуле сложных процентов. n Смешанный метод предполагает начисление процентов за целое число лет по формуле сложных процентов и за дробную часть срока по формуле простых процентов: n = a + b – срок ссуды, a – целое число лет, b – дробная часть года.

Наращение процентов т раз в году n Пусть годовая ставка равна j, число периодов начисления в году - т. Каждый раз проценты начисляются по ставке j/т. Ставку j называют номинальной. Формулу наращения имеет вид: где N — общее количество периодов начисления.

n Эффективная ставка процента - эта ставка, которая измеряет реальный относительный доход, который получают в целом за год, т. е. эффективная ставка — это годовая ставка сложных процентов, которая дает тот же результат, что и mразовое начисление процентов по ставке j / m.

n Обозначим эффективную ставку через i. По определению множители наращения по двум ставкам (эффективной и номинальной при mразовом начислении) должны быть равны другу:

Дисконтирование по сложной ставке n Если требуется определить Р по значению S по сложной ставке процентов, то на основе (1) получим n Для случаев, когда проценты начисляются т раз в году, получим

Учет по сложной учетной ставке Дисконтирование по сложной учетной ставке осуществляется по формуле d - сложная годовая учетная ставка.

Номинальная и эффективная учетные ставки Дисконтирование может производиться не один, а т раз в году, т. е. каждый раз учет производится по ставке f / т , f — номинальная годовая учетная ставка.

Эффективная учетная ставка d

Наращение по сложной учетной ставке

Постоянная сила роста n При дискретном начислении процентов т раз в году по номинальной ставке j наращенная

n Для того чтобы отличить непрерывную ставку от дискретной, обозначим силу роста как . Тогда S= n Pe

n Дискретные и непрерывные ставки наращения находятся в функциональной зависимости:

Переменная сила роста n Пусть сила роста изменяется во времени, следуя некоторому закону, представленному в виде непрерывной функции времени: t = f(t). Тогда наращенная сумма и современная величина определяются как

n Функция времени может быть самого различного вида, например линейная. В этом случае имеем Здесь - начальное значение силы роста, а - прирост силы роста в единицу времени, q - множитель наращения.