Demo Find Goal Build Map q Record initial

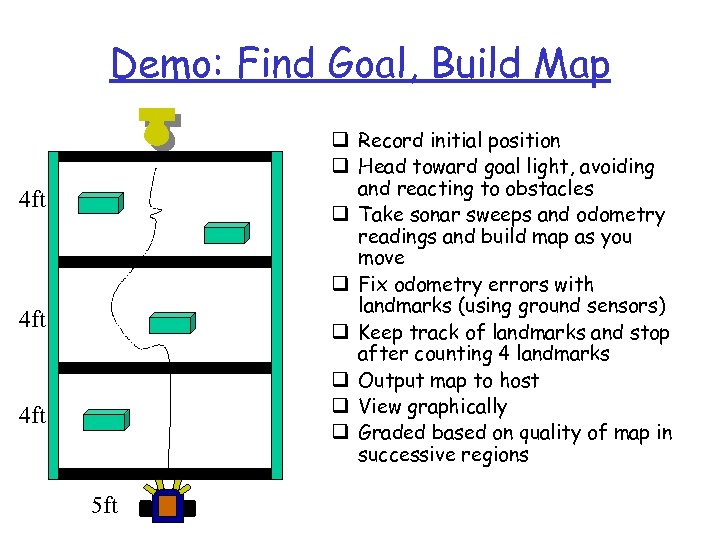
Demo: Find Goal, Build Map q Record initial position q Head toward goal light, avoiding and reacting to obstacles q Take sonar sweeps and odometry readings and build map as you move q Fix odometry errors with landmarks (using ground sensors) q Keep track of landmarks and stop after counting 4 landmarks q Output map to host q View graphically q Graded based on quality of map in successive regions 4 ft 4 ft 5 ft

Lab 9 Off-board Map Building and Path Planning http: //plan. mcs. drexel. edu/cours es/robotlab/labs/lab 09. pdf

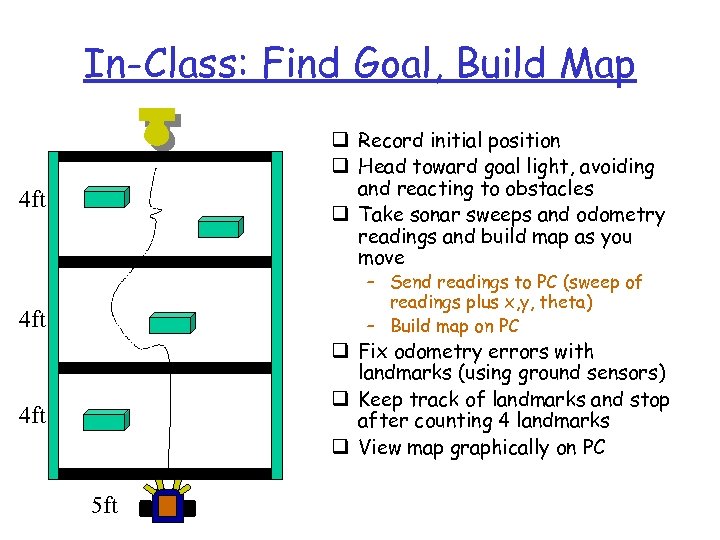
In-Class: Find Goal, Build Map q Record initial position q Head toward goal light, avoiding and reacting to obstacles q Take sonar sweeps and odometry readings and build map as you move 4 ft – Send readings to PC (sweep of readings plus x, y, theta) – Build map on PC 4 ft q Fix odometry errors with landmarks (using ground sensors) q Keep track of landmarks and stop after counting 4 landmarks q View map graphically on PC 4 ft 5 ft

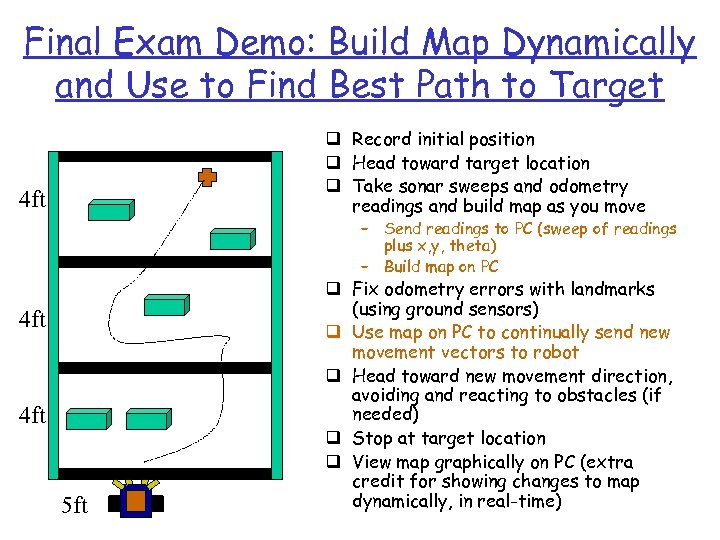
Final Exam Demo: Build Map Dynamically and Use to Find Best Path to Target q Record initial position q Head toward target location q Take sonar sweeps and odometry readings and build map as you move 4 ft – Send readings to PC (sweep of readings plus x, y, theta) – Build map on PC 4 ft 5 ft q Fix odometry errors with landmarks (using ground sensors) q Use map on PC to continually send new movement vectors to robot q Head toward new movement direction, avoiding and reacting to obstacles (if needed) q Stop at target location q View map graphically on PC (extra credit for showing changes to map dynamically, in real-time)

Today q Review global sonar maps q Review kinematics q Full duplex serial communication for offboard planning and control q Dynamic path planning with global maps

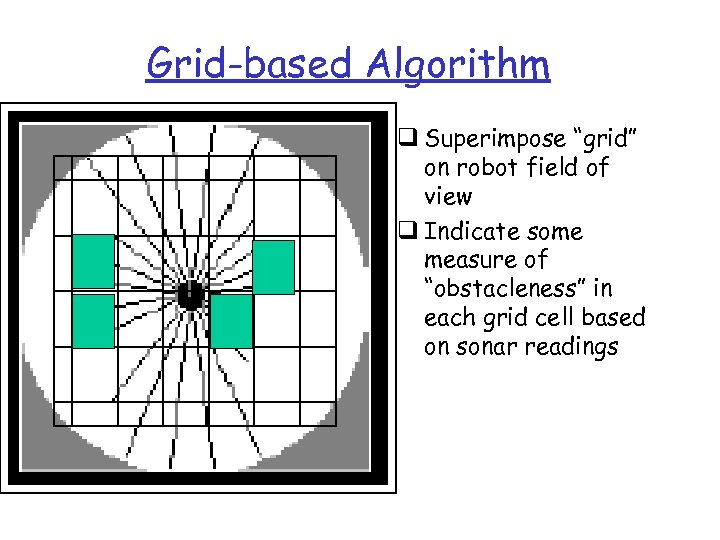
Grid-based Algorithm q Superimpose “grid” on robot field of view q Indicate some measure of “obstacleness” in each grid cell based on sonar readings

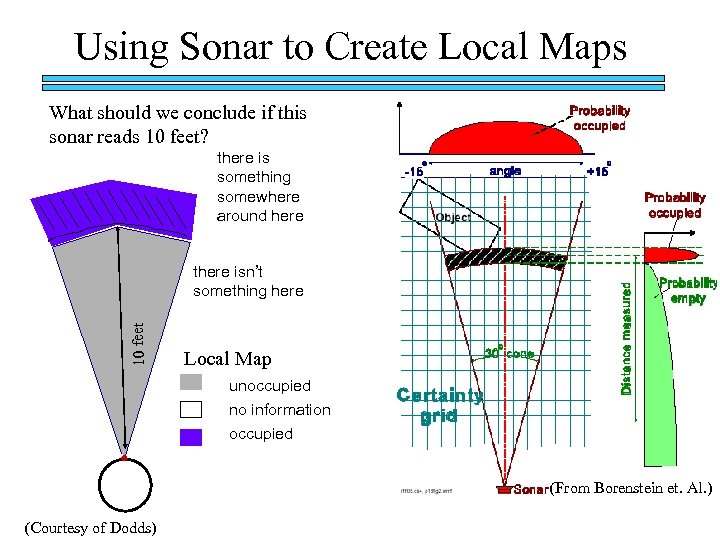
Using Sonar to Create Local Maps What should we conclude if this sonar reads 10 feet? there is something somewhere around here 10 feet there isn’t something here Local Map unoccupied no information occupied or. . . (From Borenstein et. Al. ) (Courtesy of Dodds)

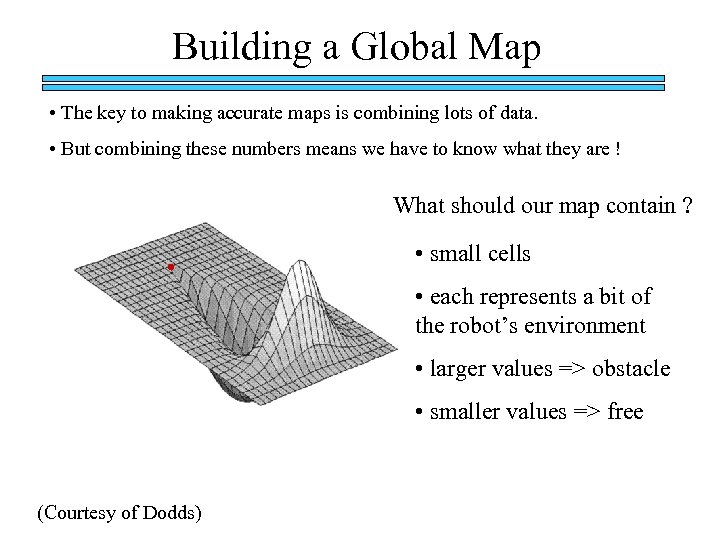
Building a Global Map • The key to making accurate maps is combining lots of data. • But combining these numbers means we have to know what they are ! What should our map contain ? • small cells • each represents a bit of the robot’s environment • larger values => obstacle • smaller values => free (Courtesy of Dodds)

Building a Global Map with Vector Field Histogram q Faster than using probabilities q Makes assumptions and approximations q Uses certainty values in each grid cell rather than occupancy probabilities q Rather than update all cells in range, only those on line of sight of sensor are updated with increment if near range reading and decrement below range reading q Cells bounded below and above (eg 0, 10) q Key observation: by taking rapid readings, this method approximates a probability distribution by sampling the real world

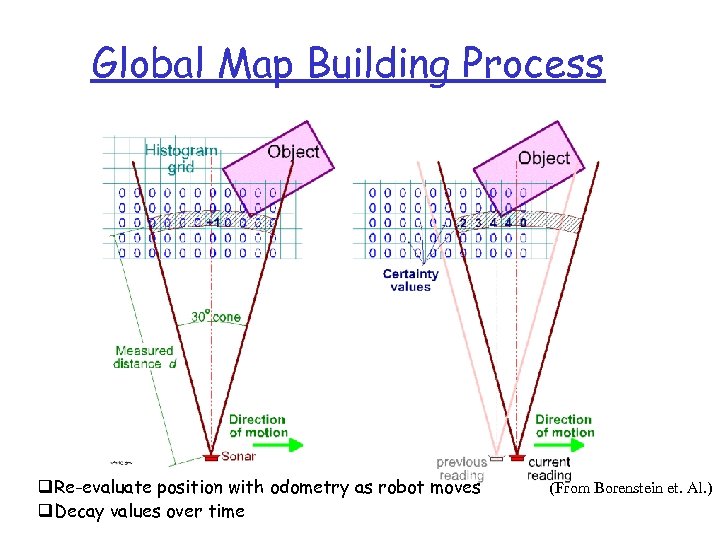
Global Map Building Process q. Re-evaluate position with odometry as robot moves q. Decay values over time (From Borenstein et. Al. )

Displaying Global Map of Occupancy Values on Host http: //plan. mcs. drexel. edu/cgibin/legorobots/occgrid. cgi

Today q Review global sonar maps q Review kinematics q Full duplex serial communication for offboard planning and control q Dynamic path planning with global maps

Review: Forward Kinematics q q Given: Starting pose (x, y, theta), Motor commands Compute: Ending pose (x’, y’, theta’) Assume encoders mounted on drive motors Let – – Cm = encoder count to linear displacement conversion factor Dn = wheel diameter Ce = encoder pulses per revolution N = gear ratio q Cm = p Dn / N Ce q Incremental travel distance for left wheel = Cm NL (NL = encoder counts on left wheel) q Incremental travel distance for right wheel = Cm NR (NR = encoder counts on right wheel) q That’s all we need for determining horizontal displacement and rotation from encoder counts

Differential Drive Odometry/Kinematics q DL = distance traveled by left wheel q DR = distance traveled by right wheel Distance traveled by center point of robot is then D = (DR+DL)/2 Change in orientation Dtheta is then (DR – DL)/base New orientation is then theta’=theta + Dtheta If old robot position is x, y new robot position is now x’ = x + D cos theta’ y’ = y + D sin theta’

Review: Localization using Kinematics q Need to know robot location during sonar sweep in order to know how to update Global Map q Issue: We can’t tell direction from encoders alone q Solution: Keep track of forward/backward motor command sent to each wheel q Localization program: Build new arrays into behavior/priority-based controller and use to continually update location

Today q Review global sonar maps q Review kinematics q Full duplex serial communication for offboard planning and control q Dynamic path planning with global maps

Review: Serial Communication Modes q Collect sensor data on Handy Board q Upload to PC host, either 1. Batch mode: program stores data on Handy Board and later writes to host using serial line 2. Real-time data collection: program on Handy Board writes data directly to serial line during data collection activities 3. On-line interaction: programs active on both Handy Board and Host communicate with each other over serial line (copyright Prentice Hall 2001)

Real-Time Interaction q No longer using terminal program q Replacing terminal program with C++ code to monitor serial port and send/receive data q Adding functions to Handy. Board to implement communications protocol with new Host program q (We also have Java code available)

Andrew’s Serial Comms API PC-side - Setup q Include “pc. Serial. h” into your c++ program. q Constructor: pc. Serial(); q Destructor: ~pc. Serial();

Andrew’s Serial Comms API PC-side – Write to Handy. Board q Write byte (unsigned char) or integer to Handyboard over serial line. – void write. Byte(BYTE c); – void write. Int(int i); // not working q Write an Array to the Handyboard (not yet working) – void write. Array(int data[], int size. Of);

Andrew’s Serial Comms API PC-side – Read from Handy. Board q Read byte (unsigned char) or integer from Handyboard over serial line. – BYTE read. Byte(); – int read. Int(); q Read an Array of integers from the Handyboard q Needs array and size of array – void read. Array(int data[], int size. Of);

Andrew’s Serial Comms API Handy. Board-side – Read from PC q Read a char or int from the PC – char serial_read. Byte() – int serial_read. Int() (not working yet!) q Read an Array from the PC (Not yet working) – void serial_read. Array(int data[], int size. Of)

Andrew’s Serial Comms API Handy. Board-side – Write to PC q Write a char or int to the PC – void serial_write. Byte(int A) – void serial_write. Int(int A) q Write an Array to the PC – void serial_write. Array(int A[], int size. Of)

To Read/Write One Int at a Time This code goes into the handyboard main() int c = 500; start_press(); while(1){ serial_write. Int(c); msleep(5 L); } This code goes into the pc main() int b; pc. Serial S; while(1){ b = S. read. Int(); cout << "b = " << b << endl; }

To Read/Write Array of Ints This code goes into the handyboard main() char c; int i; int a[90] ; start_press(); for(i=0; i<90; i++){ a[i] =1000+i; } printf("write. Array"); serial_write. Array(a, 90); This code goes into the pc main() int A[90]; pc. Serial S; cout << "S. read. Array " << endl; S. read. Array(A, 90); cout << "S. read. Array done " << endl; for(int j =0; j<90; j++){ cout << "A[" <<j << "] = " << A[j] << endl; }

Running the code: sending data from the handyboard to the pc q Start the handyboard. – Handyboard sends garbage over the serial line when it is first turned on. q Start the PC program. q Press Start on the handyboard and the data will be sent to the PC

Running the code: sending data from the pc to the handyboard q Start the Handyboard. q Press the start button. – Handyboard will wait for data to be sent to it. q Start the PC program and the data will be sent to the handyboard.

Today q Review global sonar maps q Review kinematics q Full duplex serial communication for offboard planning and control q Dynamic path planning with global maps

Off-board Map Building and Path Planning q How does the robot use Global Map + Target location to choose current heading? q Closing the Loop

Review: Closed-loop Control q Drive parallel to wall q Feedback from proximity sensors (e. g. bump, IR, sonar) q Feedback loop, continuous monitoring and correction of motors -- adjusting distance to wall to maintain goal distance (Courtesy of Bennet)

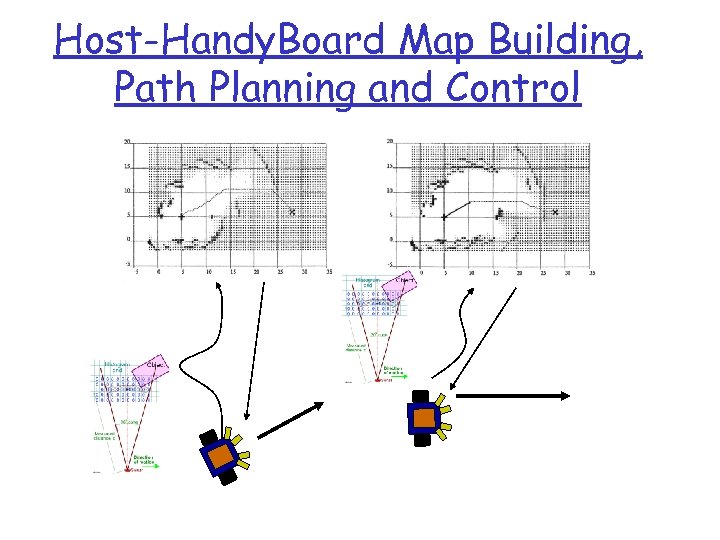
Host-Handy. Board Map Building, Path Planning and Control

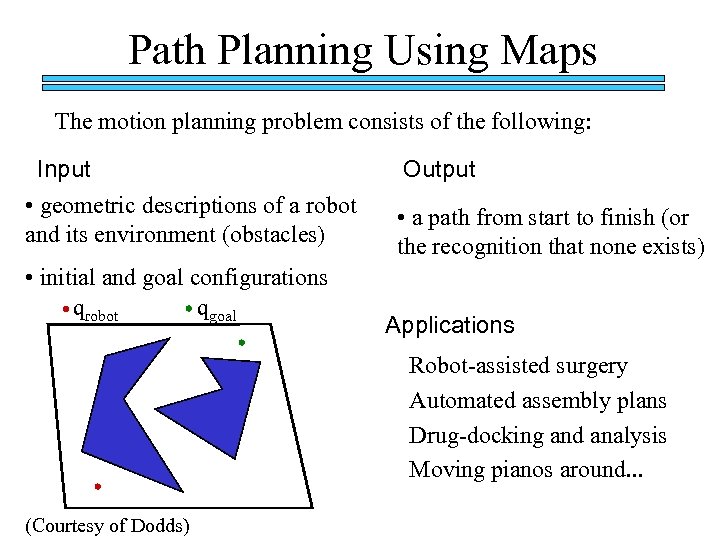
Path Planning Using Maps The motion planning problem consists of the following: Input • geometric descriptions of a robot and its environment (obstacles) • initial and goal configurations qrobot qgoal Output • a path from start to finish (or the recognition that none exists) Applications Robot-assisted surgery Automated assembly plans Drug-docking and analysis Moving pianos around. . . (Courtesy of Dodds)

Roadmap approaches Visibility graphs In a polygonal (or polyhedral) configuration space, construct all of the line segments that connect vertices to one another (and that do not intersect the obstacles themselves). Dijkstra’s algorithm Converts the problem into one of graph search. N = the number of vertices in C. Space (Courtesy of Dodds) O(N^2)

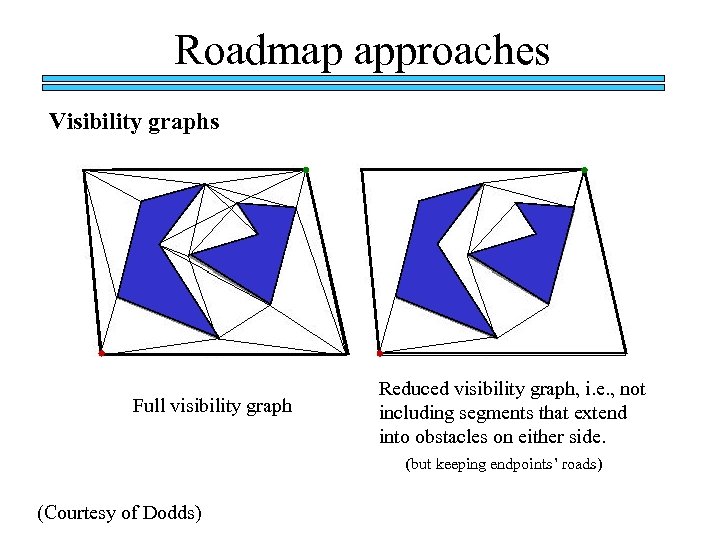
Roadmap approaches Visibility graphs Full visibility graph Reduced visibility graph, i. e. , not including segments that extend into obstacles on either side. (but keeping endpoints’ roads) (Courtesy of Dodds)

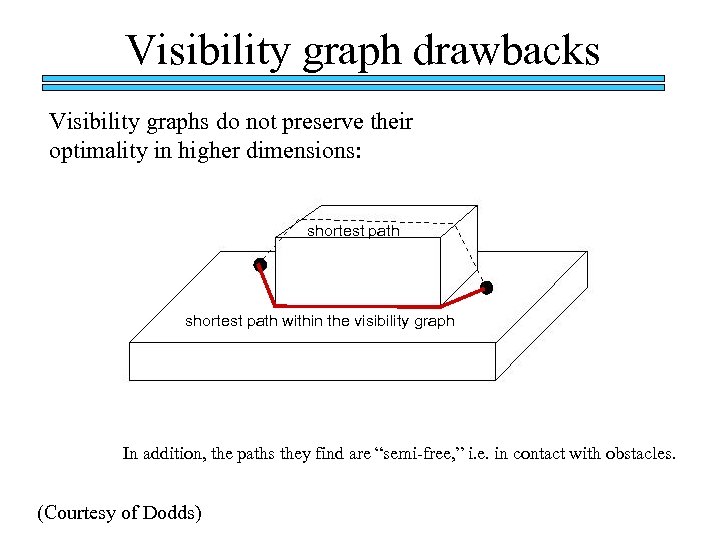
Visibility graph drawbacks Visibility graphs do not preserve their optimality in higher dimensions: shortest path within the visibility graph In addition, the paths they find are “semi-free, ” i. e. in contact with obstacles. (Courtesy of Dodds)

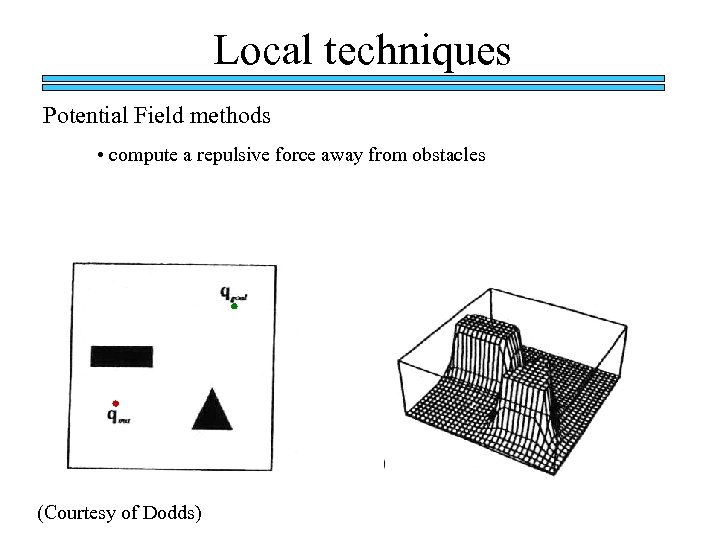
Local techniques Potential Field methods • compute a repulsive force away from obstacles (Courtesy of Dodds)

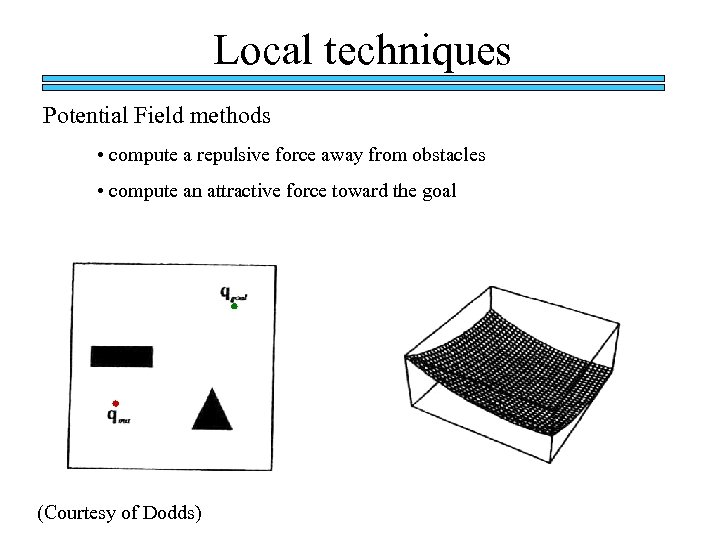
Local techniques Potential Field methods • compute a repulsive force away from obstacles • compute an attractive force toward the goal (Courtesy of Dodds)

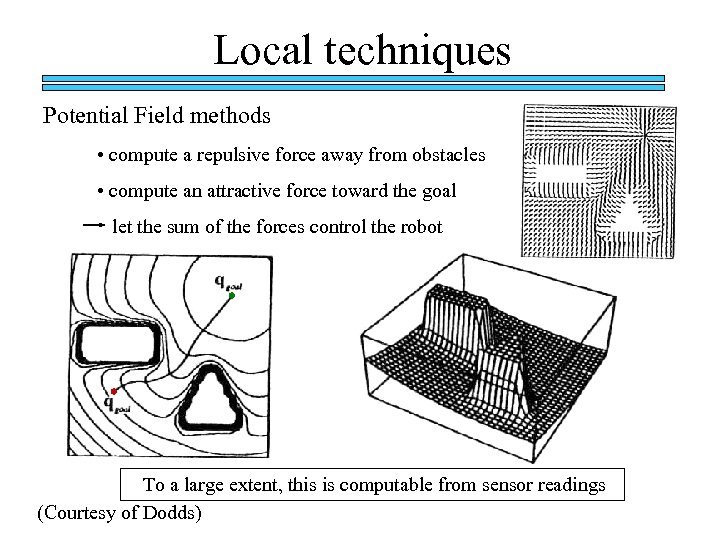
Local techniques Potential Field methods • compute a repulsive force away from obstacles • compute an attractive force toward the goal let the sum of the forces control the robot To a large extent, this is computable from sensor readings (Courtesy of Dodds)

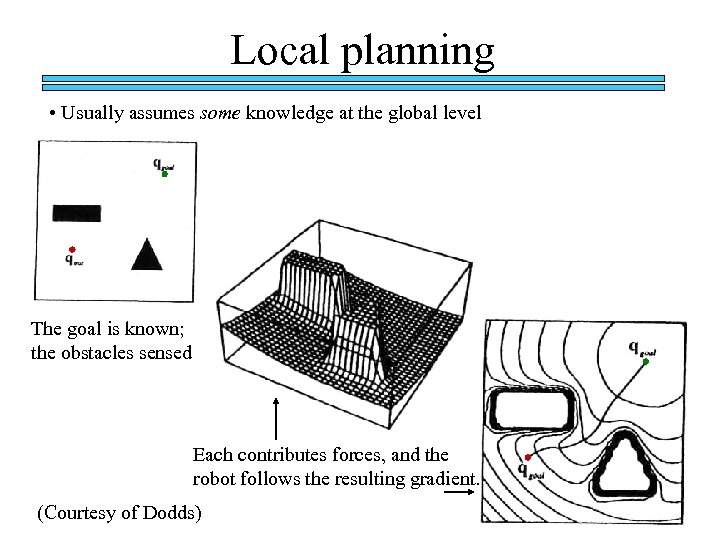
Local planning • Usually assumes some knowledge at the global level The goal is known; the obstacles sensed Each contributes forces, and the robot follows the resulting gradient. (Courtesy of Dodds)

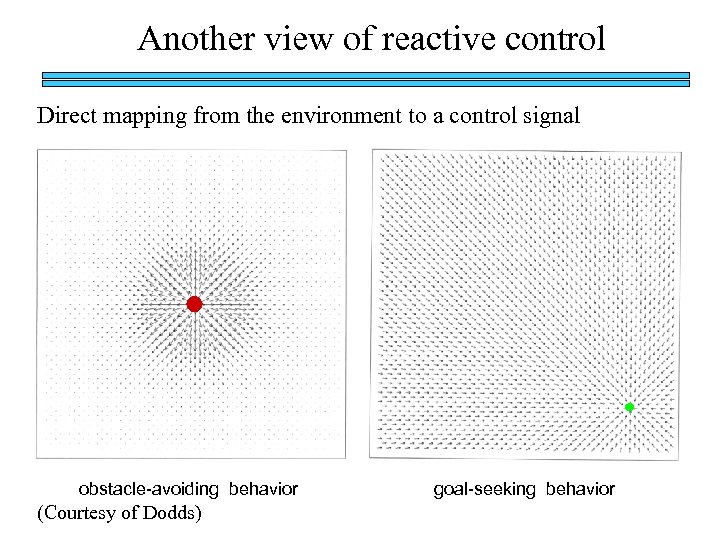
Another view of reactive control Direct mapping from the environment to a control signal obstacle-avoiding behavior (Courtesy of Dodds) goal-seeking behavior

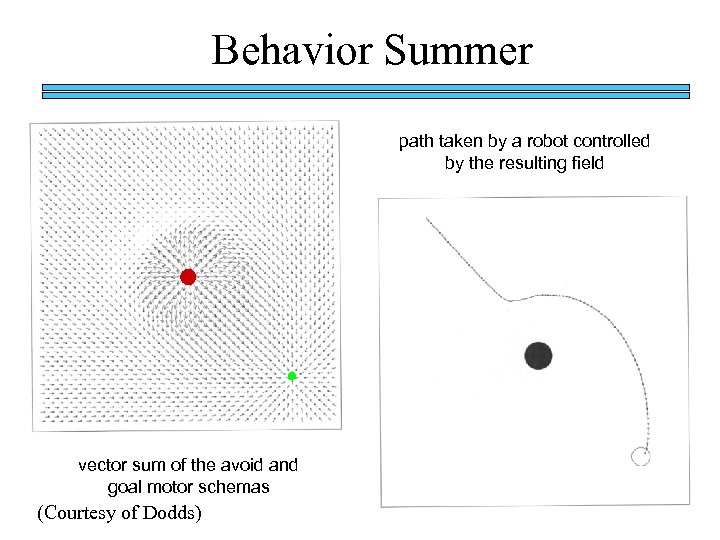
Behavior Summer path taken by a robot controlled by the resulting field vector sum of the avoid and goal motor schemas (Courtesy of Dodds)

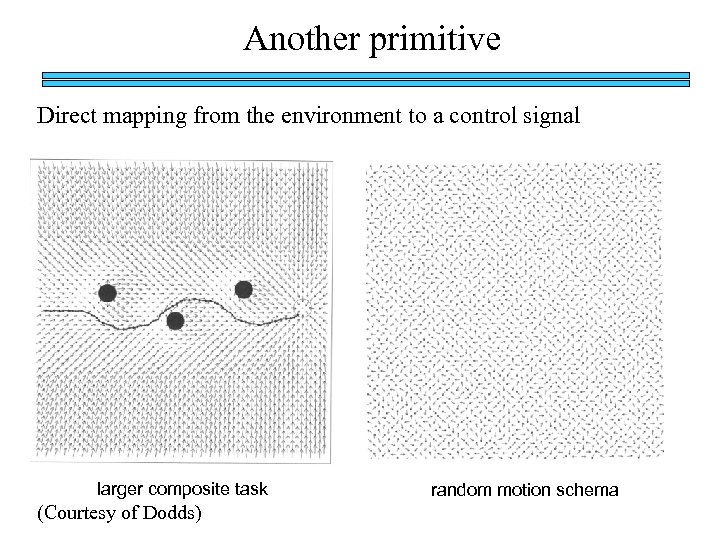
Another primitive Direct mapping from the environment to a control signal larger composite task (Courtesy of Dodds) random motion schema

Local minima Noise allows a system to “jump out” of local minima. the problem (Courtesy of Dodds) a solution

Path Planning in Evidence Grids Reduces to a search problem within the graph of cells, and the graph is created on the fly. Search for a minimumcost path, depending on • length • probability of collision • Can use many different path planning algorithms • We will use potential-fieldlike force summing • Note: need to compute vectors for sequence of moves around robot’s current location (policy) (Courtesy of Dodds)

Lab 9 Off-board Map Building and Path Planning http: //plan. mcs. drexel. edu/cours es/robotlab/labs/lab 09. pdf

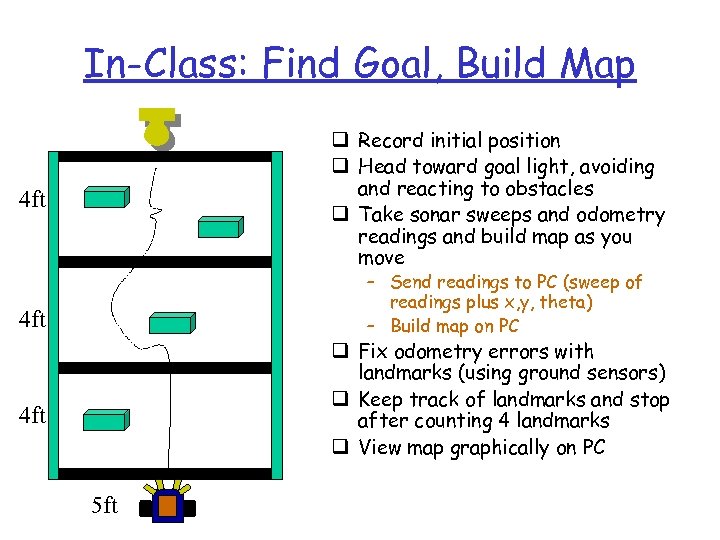
In-Class: Find Goal, Build Map q Record initial position q Head toward goal light, avoiding and reacting to obstacles q Take sonar sweeps and odometry readings and build map as you move 4 ft – Send readings to PC (sweep of readings plus x, y, theta) – Build map on PC 4 ft q Fix odometry errors with landmarks (using ground sensors) q Keep track of landmarks and stop after counting 4 landmarks q View map graphically on PC 4 ft 5 ft

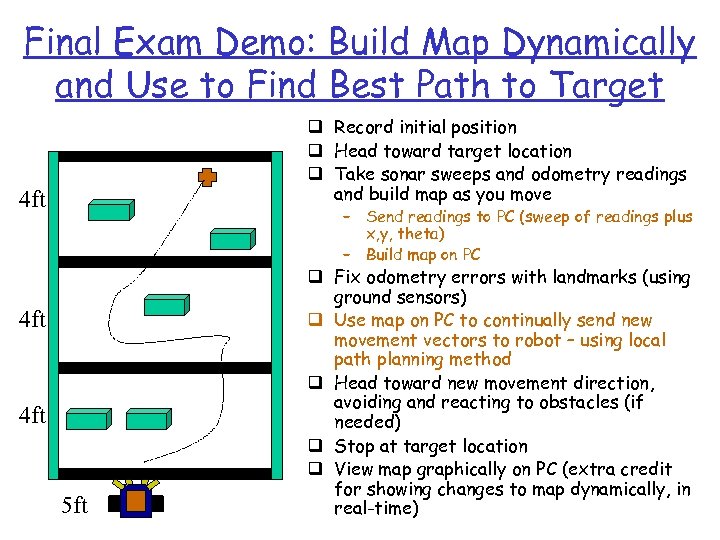
Final Exam Demo: Build Map Dynamically and Use to Find Best Path to Target q Record initial position q Head toward target location q Take sonar sweeps and odometry readings and build map as you move 4 ft – Send readings to PC (sweep of readings plus x, y, theta) – Build map on PC 4 ft 5 ft q Fix odometry errors with landmarks (using ground sensors) q Use map on PC to continually send new movement vectors to robot – using local path planning method q Head toward new movement direction, avoiding and reacting to obstacles (if needed) q Stop at target location q View map graphically on PC (extra credit for showing changes to map dynamically, in real-time)

Final Projects and Reports q Significant portion of grade (~3 labs or so) q Due Wednesday of Finals Week q Undergraduates: Report on Final Exam Robot, including: – Code – … to be filled in soon q Graduate Students: Demo of Final Project, Report on Final Project, including: – Code – … to be filled in soon

References q http: //plan. mcs. drexel. edu/courses/robotl ab/labs/lab 09. pdf q http: //plan. mcs. drexel. edu/courses/robotl ab/readings/hbmanual. pdf q http: //plan. mcs. drexel. edu/courses/readin gs