cf8816dddd6ec7daf30b766bded36747.ppt
- Количество слайдов: 117
 Demand & Utility
Demand & Utility
 What is Utility? Satisfaction, happiness, benefit
What is Utility? Satisfaction, happiness, benefit
 Cardinal Utility vs. Ordinal Utility Cardinal Utility: Assigning numerical values to the amount of satisfaction Ordinal Utility: Not assigning numerical values to the amount of satisfaction but indicating the order of preferences, that is, what is preferred to what
Cardinal Utility vs. Ordinal Utility Cardinal Utility: Assigning numerical values to the amount of satisfaction Ordinal Utility: Not assigning numerical values to the amount of satisfaction but indicating the order of preferences, that is, what is preferred to what
 Util A unit of measure of utility
Util A unit of measure of utility
 Total Utility The amount of satisfaction obtained by consuming specified amounts of a product period of time.
Total Utility The amount of satisfaction obtained by consuming specified amounts of a product period of time.
 Example: TU(X) = 16 X – X 2 where X is the amount a good that is consumed in a given period of time. 5 units of the product period of time yields 55 utils of satisfaction
Example: TU(X) = 16 X – X 2 where X is the amount a good that is consumed in a given period of time. 5 units of the product period of time yields 55 utils of satisfaction
 Marginal Utility The change in total utility ( TU) resulting from a one unit change in consumption ( X). MU = TU/ X
Marginal Utility The change in total utility ( TU) resulting from a one unit change in consumption ( X). MU = TU/ X
 Diminishing Marginal Utility Each additional unit of a product contributes less extra utility than the previous unit.
Diminishing Marginal Utility Each additional unit of a product contributes less extra utility than the previous unit.
 When the changes in consumption are infinitesimally small, marginal utility is the derivative of total utility. MU = d. TU/d. X
When the changes in consumption are infinitesimally small, marginal utility is the derivative of total utility. MU = d. TU/d. X
 Calculating MU from a TU Function Example: TU(X) = 16 X – X 2 MU = d. TU/d. X = 16 -2 X
Calculating MU from a TU Function Example: TU(X) = 16 X – X 2 MU = d. TU/d. X = 16 -2 X
 In general, the derivative of a total function is the marginal function. The marginal function is the slope of the total function.
In general, the derivative of a total function is the marginal function. The marginal function is the slope of the total function.
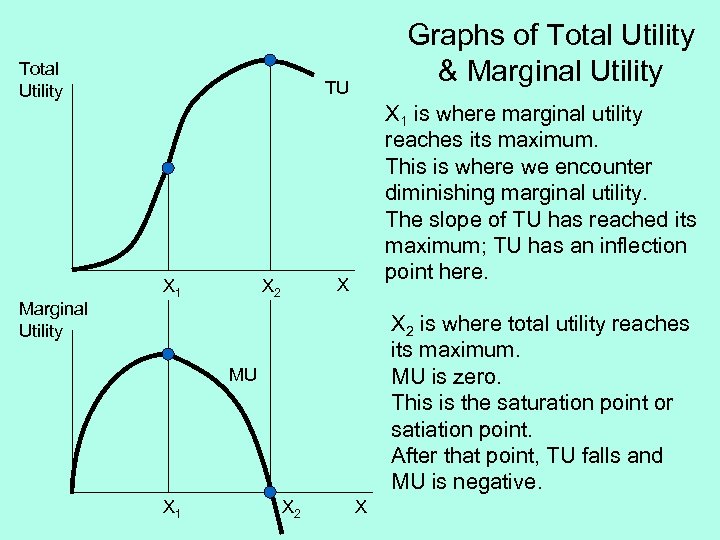 Total Utility Marginal Utility Graphs of Total Utility & Marginal Utility TU X 1 is where marginal utility reaches its maximum. This is where we encounter diminishing marginal utility. The slope of TU has reached its maximum; TU has an inflection point here. X X 2 is where total utility reaches its maximum. MU is zero. This is the saturation point or satiation point. After that point, TU falls and MU is negative. MU X 1 X 2 X
Total Utility Marginal Utility Graphs of Total Utility & Marginal Utility TU X 1 is where marginal utility reaches its maximum. This is where we encounter diminishing marginal utility. The slope of TU has reached its maximum; TU has an inflection point here. X X 2 is where total utility reaches its maximum. MU is zero. This is the saturation point or satiation point. After that point, TU falls and MU is negative. MU X 1 X 2 X
 Example: If TU = 15 X + 7 X 2 – (1/3) X 3, find (a) the MU function, (b) the point of diminishing marginal utility, & (c) the satiation point. a. b. MU = d. TU/d. X = 15 +14 X – X 2 Diminishing MU is where MU has a maximum, or the derivative of MU is zero. 0 = d. MU/dx = 14 – 2 X X=7 c. Satiation is where TU reaches a maximum or its derivative (which is MU) is zero. How do we determine where MU = 15 +14 X – X 2 = 0 ?
Example: If TU = 15 X + 7 X 2 – (1/3) X 3, find (a) the MU function, (b) the point of diminishing marginal utility, & (c) the satiation point. a. b. MU = d. TU/d. X = 15 +14 X – X 2 Diminishing MU is where MU has a maximum, or the derivative of MU is zero. 0 = d. MU/dx = 14 – 2 X X=7 c. Satiation is where TU reaches a maximum or its derivative (which is MU) is zero. How do we determine where MU = 15 +14 X – X 2 = 0 ?
 Apply Quadratic Formula to –X 2 + 14 X + 15 = 0. Since a negative amount of a product makes no sense, X must equal 15.
Apply Quadratic Formula to –X 2 + 14 X + 15 = 0. Since a negative amount of a product makes no sense, X must equal 15.
 If the previous example were about eating free cookies at a party, you’d eat 15 of them. That is where you become satiated. After 15 cookies, you begin to feel a bit bloated.
If the previous example were about eating free cookies at a party, you’d eat 15 of them. That is where you become satiated. After 15 cookies, you begin to feel a bit bloated.
 When you have more than one product, the marginal utility is a partial derivative. Calculating partial derivatives is no more difficult than calculating other derivatives. You just treat all variables as constants, except the one with which you are taking the derivative. We denote the partial derivative of Z with respect to X as Z/ X instead of d. Z/d. X. Example: Z = X 2 +3 XY + 5 Y 3 To take the partial derivative with respect to X, pretend Y is a constant (like 4). Then, Z/ X = 2 X + 3 Y. Similarly, to take the partial derivative with respect to Y, pretend X is a constant (like 4). So, Z/ Y = 3 X + 15 Y 2.
When you have more than one product, the marginal utility is a partial derivative. Calculating partial derivatives is no more difficult than calculating other derivatives. You just treat all variables as constants, except the one with which you are taking the derivative. We denote the partial derivative of Z with respect to X as Z/ X instead of d. Z/d. X. Example: Z = X 2 +3 XY + 5 Y 3 To take the partial derivative with respect to X, pretend Y is a constant (like 4). Then, Z/ X = 2 X + 3 Y. Similarly, to take the partial derivative with respect to Y, pretend X is a constant (like 4). So, Z/ Y = 3 X + 15 Y 2.
 The Connection between Demand Utility Instead of thinking in terms of utils, let’s think in terms of dollars. Suppose the purchase of one unit of a good gives you $10 worth of satisfaction. In other words, the marginal utility of that first unit of the good is $10. Then you would be willing to pay up to $10 for it.
The Connection between Demand Utility Instead of thinking in terms of utils, let’s think in terms of dollars. Suppose the purchase of one unit of a good gives you $10 worth of satisfaction. In other words, the marginal utility of that first unit of the good is $10. Then you would be willing to pay up to $10 for it.
 If a second unit of the good contributes $8 more of satisfaction, the marginal utility of your second unit is $8 and you would be willing to pay up to $8 for it. If a third unit of the good contributes $6 more of satisfaction, the marginal utility of your third unit is $6 and you would be willing to pay up to $6 for it.
If a second unit of the good contributes $8 more of satisfaction, the marginal utility of your second unit is $8 and you would be willing to pay up to $8 for it. If a third unit of the good contributes $6 more of satisfaction, the marginal utility of your third unit is $6 and you would be willing to pay up to $6 for it.
 Remember that the demand curve tells you what people are willing to pay for various amounts of a good or, equivalently, how many units of a good they are willing to purchase at various prices. So, since we just found that the marginal utility tells us what we are willing to pay for a good, the marginal utility provides us with information that we can use to determine our demand curve.
Remember that the demand curve tells you what people are willing to pay for various amounts of a good or, equivalently, how many units of a good they are willing to purchase at various prices. So, since we just found that the marginal utility tells us what we are willing to pay for a good, the marginal utility provides us with information that we can use to determine our demand curve.
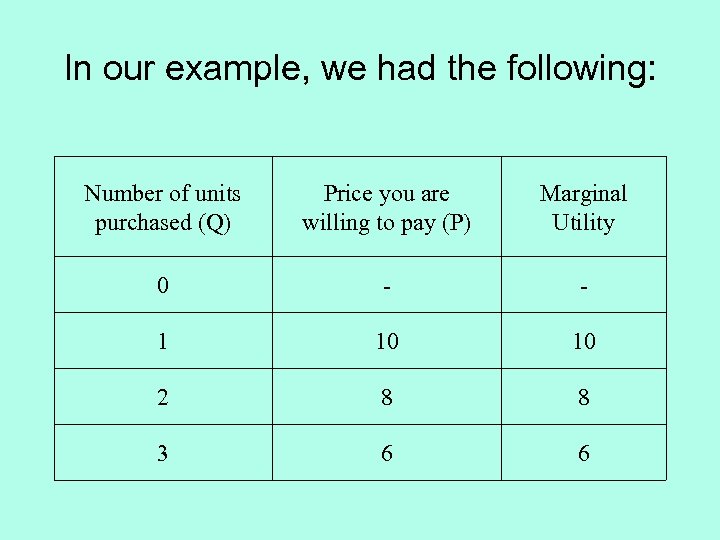 In our example, we had the following: Number of units purchased (Q) Price you are willing to pay (P) Marginal Utility 0 - - 1 10 10 2 8 8 3 6 6
In our example, we had the following: Number of units purchased (Q) Price you are willing to pay (P) Marginal Utility 0 - - 1 10 10 2 8 8 3 6 6
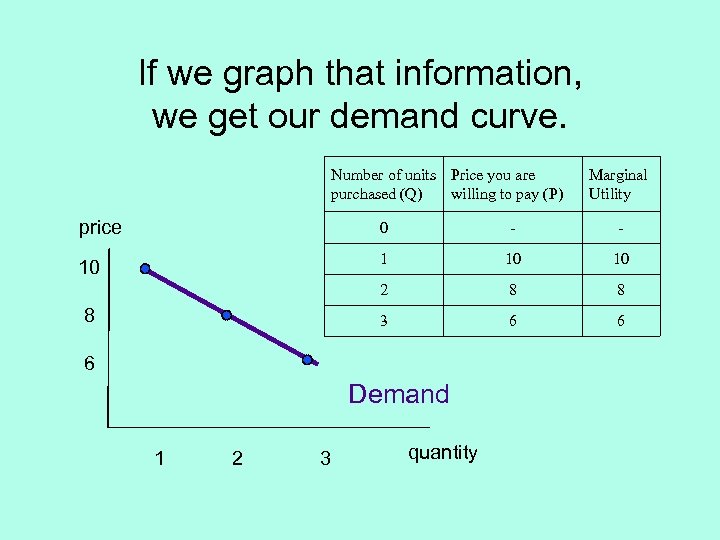 If we graph that information, we get our demand curve. Number of units Price you are purchased (Q) willing to pay (P) Marginal Utility price 0 - - 10 10 2 8 8 3 6 6 8 6 Demand 1 2 3 quantity
If we graph that information, we get our demand curve. Number of units Price you are purchased (Q) willing to pay (P) Marginal Utility price 0 - - 10 10 2 8 8 3 6 6 8 6 Demand 1 2 3 quantity
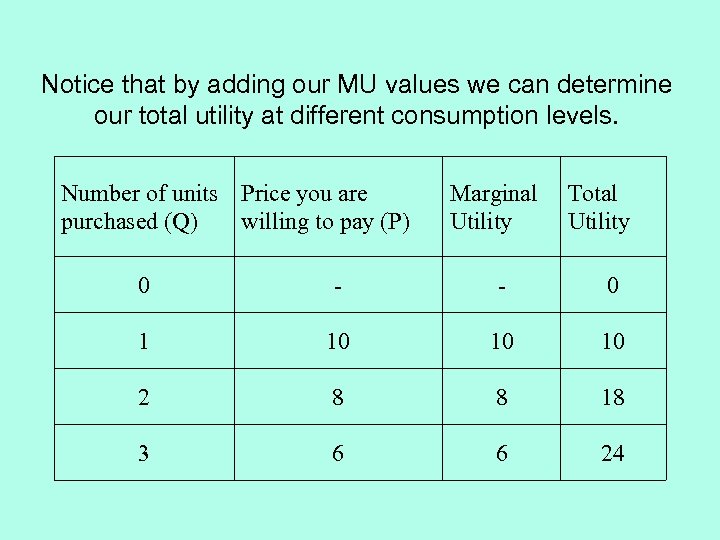 Notice that by adding our MU values we can determine our total utility at different consumption levels. Number of units Price you are purchased (Q) willing to pay (P) Marginal Utility Total Utility 0 - - 0 1 10 10 10 2 8 8 18 3 6 6 24
Notice that by adding our MU values we can determine our total utility at different consumption levels. Number of units Price you are purchased (Q) willing to pay (P) Marginal Utility Total Utility 0 - - 0 1 10 10 10 2 8 8 18 3 6 6 24
 Indifference Curve A set of combinations of goods that are viewed as equally satisfactory by the consumer.
Indifference Curve A set of combinations of goods that are viewed as equally satisfactory by the consumer.
 Indifference Map A collection of indifference curves
Indifference Map A collection of indifference curves
 Assumptions 1. The consumer can rank all bundles of commodities. 2. If bundle A is preferred to bundle B and B is preferred to C, then A is preferred to C. (This property is called transitivity. ) 3. More is better.
Assumptions 1. The consumer can rank all bundles of commodities. 2. If bundle A is preferred to bundle B and B is preferred to C, then A is preferred to C. (This property is called transitivity. ) 3. More is better.
 Characteristics of indifference curves
Characteristics of indifference curves
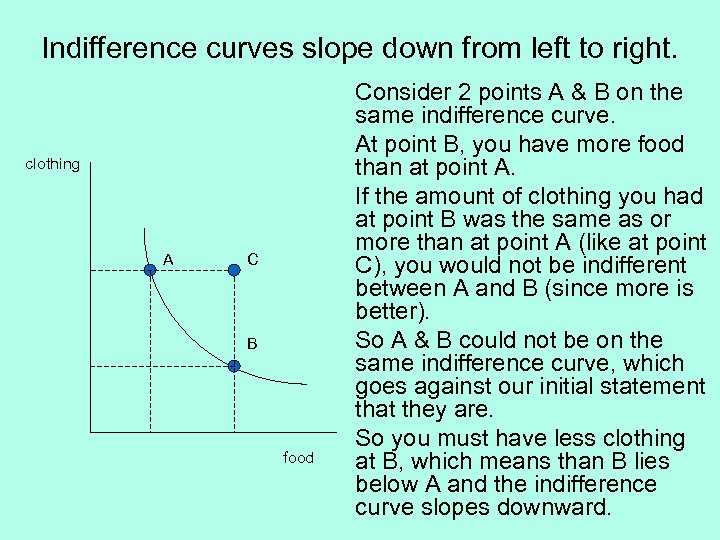 Indifference curves slope down from left to right. clothing A C B food Consider 2 points A & B on the same indifference curve. At point B, you have more food than at point A. If the amount of clothing you had at point B was the same as or more than at point A (like at point C), you would not be indifferent between A and B (since more is better). So A & B could not be on the same indifference curve, which goes against our initial statement that they are. So you must have less clothing at B, which means than B lies below A and the indifference curve slopes downward.
Indifference curves slope down from left to right. clothing A C B food Consider 2 points A & B on the same indifference curve. At point B, you have more food than at point A. If the amount of clothing you had at point B was the same as or more than at point A (like at point C), you would not be indifferent between A and B (since more is better). So A & B could not be on the same indifference curve, which goes against our initial statement that they are. So you must have less clothing at B, which means than B lies below A and the indifference curve slopes downward.
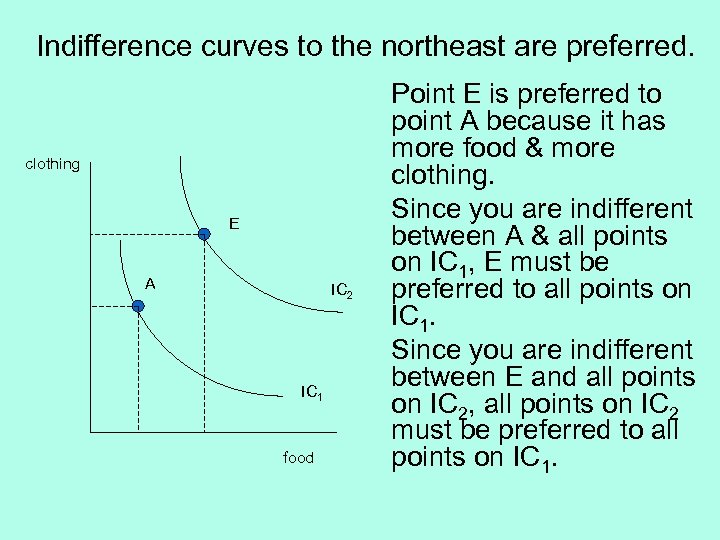 Indifference curves to the northeast are preferred. clothing E A IC 2 IC 1 food Point E is preferred to point A because it has more food & more clothing. Since you are indifferent between A & all points on IC 1, E must be preferred to all points on IC 1. Since you are indifferent between E and all points on IC 2, all points on IC 2 must be preferred to all points on IC 1.
Indifference curves to the northeast are preferred. clothing E A IC 2 IC 1 food Point E is preferred to point A because it has more food & more clothing. Since you are indifferent between A & all points on IC 1, E must be preferred to all points on IC 1. Since you are indifferent between E and all points on IC 2, all points on IC 2 must be preferred to all points on IC 1.
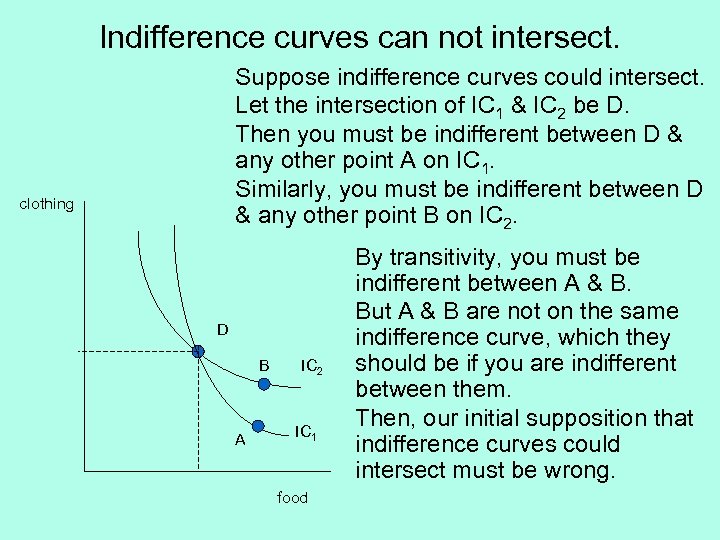 Indifference curves can not intersect. Suppose indifference curves could intersect. Let the intersection of IC 1 & IC 2 be D. Then you must be indifferent between D & any other point A on IC 1. Similarly, you must be indifferent between D & any other point B on IC 2. clothing D B A IC 2 IC 1 food By transitivity, you must be indifferent between A & B. But A & B are not on the same indifference curve, which they should be if you are indifferent between them. Then, our initial supposition that indifference curves could intersect must be wrong.
Indifference curves can not intersect. Suppose indifference curves could intersect. Let the intersection of IC 1 & IC 2 be D. Then you must be indifferent between D & any other point A on IC 1. Similarly, you must be indifferent between D & any other point B on IC 2. clothing D B A IC 2 IC 1 food By transitivity, you must be indifferent between A & B. But A & B are not on the same indifference curve, which they should be if you are indifferent between them. Then, our initial supposition that indifference curves could intersect must be wrong.
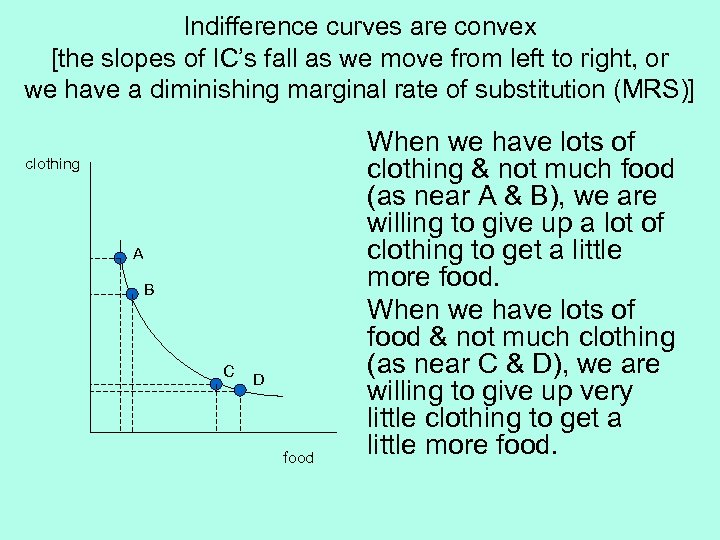 Indifference curves are convex [the slopes of IC’s fall as we move from left to right, or we have a diminishing marginal rate of substitution (MRS)] clothing A B C D food When we have lots of clothing & not much food (as near A & B), we are willing to give up a lot of clothing to get a little more food. When we have lots of food & not much clothing (as near C & D), we are willing to give up very little clothing to get a little more food.
Indifference curves are convex [the slopes of IC’s fall as we move from left to right, or we have a diminishing marginal rate of substitution (MRS)] clothing A B C D food When we have lots of clothing & not much food (as near A & B), we are willing to give up a lot of clothing to get a little more food. When we have lots of food & not much clothing (as near C & D), we are willing to give up very little clothing to get a little more food.
 Odd special cases that are not consistent with the characteristics listed previously.
Odd special cases that are not consistent with the characteristics listed previously.
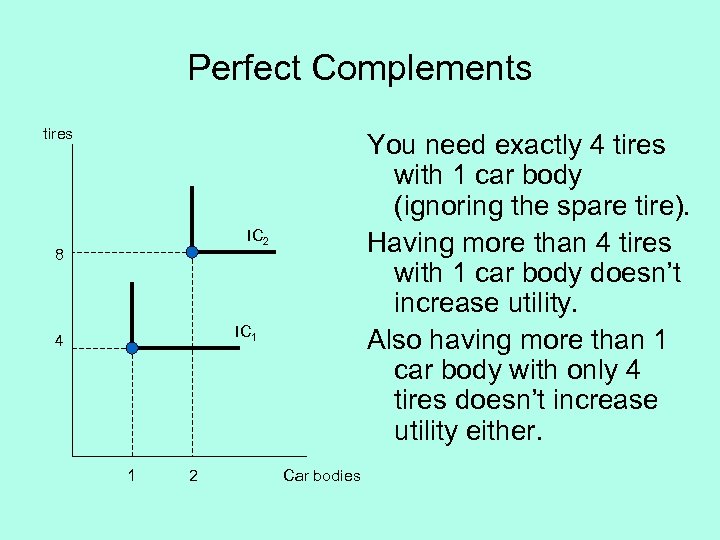 Perfect Complements tires You need exactly 4 tires with 1 car body (ignoring the spare tire). Having more than 4 tires with 1 car body doesn’t increase utility. Also having more than 1 car body with only 4 tires doesn’t increase utility either. IC 2 8 IC 1 4 1 2 Car bodies
Perfect Complements tires You need exactly 4 tires with 1 car body (ignoring the spare tire). Having more than 4 tires with 1 car body doesn’t increase utility. Also having more than 1 car body with only 4 tires doesn’t increase utility either. IC 2 8 IC 1 4 1 2 Car bodies
 Perfect Substitutes Mini-packs 10 5 IC 1 1 IC 2 2 Jumbo packs Consider two packs of paper; the mini-pack has 100 sheets & the jumbo pack has 500 sheets. No matter how many mini-packs or jumbo packs you have, you are always willing to trade 5 mini -packs for 1 jumbo pack. Since the rate at which you’re willing to trade is the slope of the IC, and that rate is constant, your IC’s have a constant slope. That means they are straight lines.
Perfect Substitutes Mini-packs 10 5 IC 1 1 IC 2 2 Jumbo packs Consider two packs of paper; the mini-pack has 100 sheets & the jumbo pack has 500 sheets. No matter how many mini-packs or jumbo packs you have, you are always willing to trade 5 mini -packs for 1 jumbo pack. Since the rate at which you’re willing to trade is the slope of the IC, and that rate is constant, your IC’s have a constant slope. That means they are straight lines.
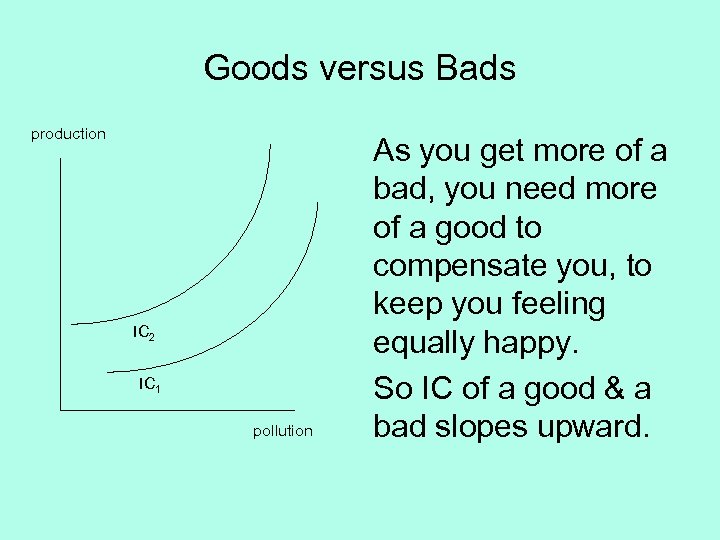 Goods versus Bads production IC 2 IC 1 pollution As you get more of a bad, you need more of a good to compensate you, to keep you feeling equally happy. So IC of a good & a bad slopes upward.
Goods versus Bads production IC 2 IC 1 pollution As you get more of a bad, you need more of a good to compensate you, to keep you feeling equally happy. So IC of a good & a bad slopes upward.
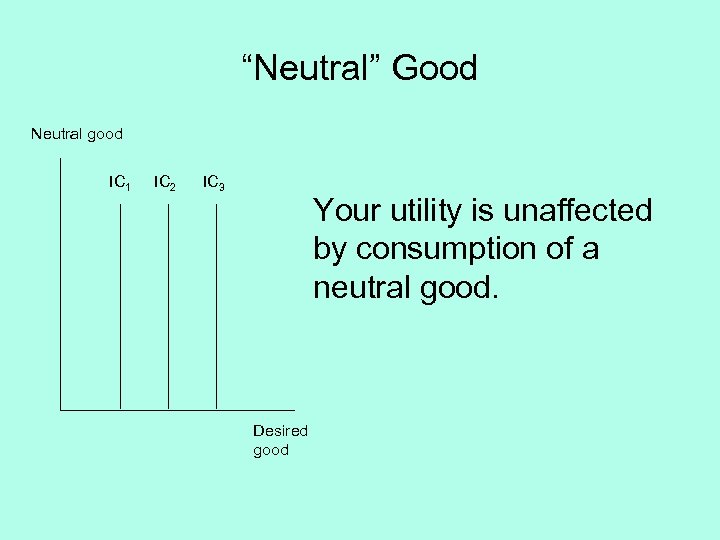 “Neutral” Good Neutral good IC 1 IC 2 IC 3 Your utility is unaffected by consumption of a neutral good. Desired good
“Neutral” Good Neutral good IC 1 IC 2 IC 3 Your utility is unaffected by consumption of a neutral good. Desired good
 Addict Substance 1 Substance 2 The more substance 1 the addict has the more he/she is willing to give up of substance 2 to get a little more of 1 (& vice versa). So the IC’s are concave instead of convex.
Addict Substance 1 Substance 2 The more substance 1 the addict has the more he/she is willing to give up of substance 2 to get a little more of 1 (& vice versa). So the IC’s are concave instead of convex.
 The slope of the indifference curve is the rate at which you are willing to trade off one good to get another good. It is called the marginal rate of substitution or MRS.
The slope of the indifference curve is the rate at which you are willing to trade off one good to get another good. It is called the marginal rate of substitution or MRS.
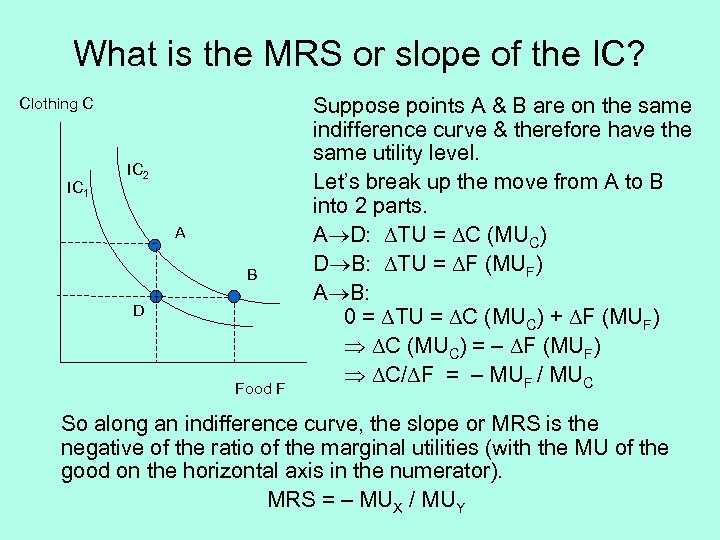 What is the MRS or slope of the IC? Clothing C IC 1 IC 2 A B D Food F Suppose points A & B are on the same indifference curve & therefore have the same utility level. Let’s break up the move from A to B into 2 parts. A D: TU = C (MUC) D B: TU = F (MUF) A B: 0 = TU = C (MUC) + F (MUF) C (MUC) = – F (MUF) C/ F = – MUF / MUC So along an indifference curve, the slope or MRS is the negative of the ratio of the marginal utilities (with the MU of the good on the horizontal axis in the numerator). MRS = – MUX / MUY
What is the MRS or slope of the IC? Clothing C IC 1 IC 2 A B D Food F Suppose points A & B are on the same indifference curve & therefore have the same utility level. Let’s break up the move from A to B into 2 parts. A D: TU = C (MUC) D B: TU = F (MUF) A B: 0 = TU = C (MUC) + F (MUF) C (MUC) = – F (MUF) C/ F = – MUF / MUC So along an indifference curve, the slope or MRS is the negative of the ratio of the marginal utilities (with the MU of the good on the horizontal axis in the numerator). MRS = – MUX / MUY
 For example, Clothing C IC 1 =90 IC 2 = 96 A 6 B 5 D 7 9 Food F Suppose IC 1 is the 90 -util indifference curve & IC 2 is the 96 -util indifference curve. Point A is 7 units of food & 6 of clothing. B is 9 units of food & 5 of clothing. Since an additional unit of clothing gives you 6 more utils of satisfaction, the MU of clothing must be 6. Since an additional 2 units of food also give you 6 more utils of satisfaction, the MU of food must be 3. So, MRS = – MUF / MUC = -3/6 = -0. 5. You’d give up 2 units of food to get 1 units of clothing.
For example, Clothing C IC 1 =90 IC 2 = 96 A 6 B 5 D 7 9 Food F Suppose IC 1 is the 90 -util indifference curve & IC 2 is the 96 -util indifference curve. Point A is 7 units of food & 6 of clothing. B is 9 units of food & 5 of clothing. Since an additional unit of clothing gives you 6 more utils of satisfaction, the MU of clothing must be 6. Since an additional 2 units of food also give you 6 more utils of satisfaction, the MU of food must be 3. So, MRS = – MUF / MUC = -3/6 = -0. 5. You’d give up 2 units of food to get 1 units of clothing.
 Budget Constraint or Budget Line This equation tells you what you can buy. For example, suppose you have $24, & there are two goods. The price of the first good is $3 per unit & the price of the second good is $4 per unit. So, if you buy X units of the first good for $3 each, you spend 3 X on that good. Similarly, if you buy Y units of the second good, you spend 4 Y on that good. Your total spending is 3 X+4 Y. If you spend all 24 dollars that you have, 3 X+4 Y=24. That equation is your budget constraint.
Budget Constraint or Budget Line This equation tells you what you can buy. For example, suppose you have $24, & there are two goods. The price of the first good is $3 per unit & the price of the second good is $4 per unit. So, if you buy X units of the first good for $3 each, you spend 3 X on that good. Similarly, if you buy Y units of the second good, you spend 4 Y on that good. Your total spending is 3 X+4 Y. If you spend all 24 dollars that you have, 3 X+4 Y=24. That equation is your budget constraint.
 Example: Budget constraint for $24 of income, and $3 & $4 for the prices of the two goods. Y (0, 6) 0 If you spent all $24 on the 1 st good, you could buy 8 units. If you spent all $24 on the 2 nd good, you could buy 6 units. So we have the intercepts of the budget constraint. The slope of the line connecting these two points is Y/ X = – 6/8 = – 3/4 = – 0. 75. (8, 0) X
Example: Budget constraint for $24 of income, and $3 & $4 for the prices of the two goods. Y (0, 6) 0 If you spent all $24 on the 1 st good, you could buy 8 units. If you spent all $24 on the 2 nd good, you could buy 6 units. So we have the intercepts of the budget constraint. The slope of the line connecting these two points is Y/ X = – 6/8 = – 3/4 = – 0. 75. (8, 0) X
 Let’s generalize. Keep in mind that income was $24 and the prices of the goods were $3 & $4. The equation of the budget constraint in our example was 3 X + 4 Y = 24. Y (0, 6) 0 So the budget constraint is p 1 X + p 2 Y = I Solving for Y in terms of X, p 2 Y = I – p 1 X, or Y = I /p 2 – (p 1/p 2)X So from our slope-intercept form, we see that the intercept is I /p 2, and the slope is –p 1/p 2. The intercept is income divided by the price of the good on the vertical axis. The slope is the negative of the ratio of the prices, with the price of the good on the horizontal axis in the numerator. (8, 0) X
Let’s generalize. Keep in mind that income was $24 and the prices of the goods were $3 & $4. The equation of the budget constraint in our example was 3 X + 4 Y = 24. Y (0, 6) 0 So the budget constraint is p 1 X + p 2 Y = I Solving for Y in terms of X, p 2 Y = I – p 1 X, or Y = I /p 2 – (p 1/p 2)X So from our slope-intercept form, we see that the intercept is I /p 2, and the slope is –p 1/p 2. The intercept is income divided by the price of the good on the vertical axis. The slope is the negative of the ratio of the prices, with the price of the good on the horizontal axis in the numerator. (8, 0) X
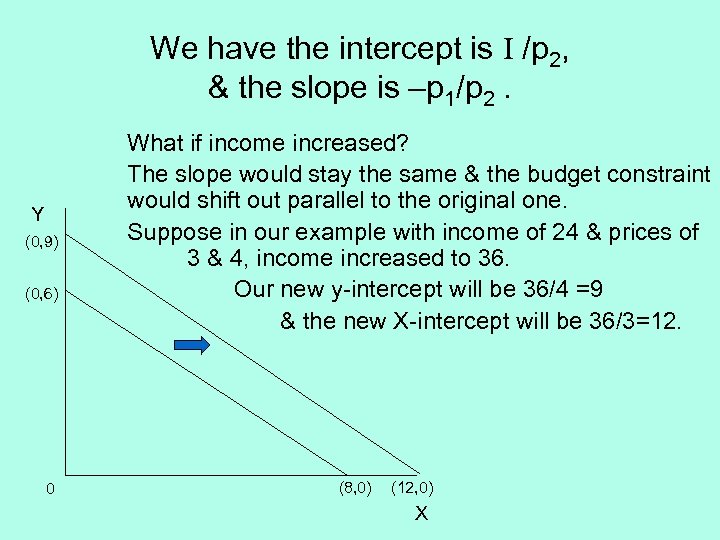 We have the intercept is I /p 2, & the slope is –p 1/p 2. Y (0, 9) (0, 6) 0 What if income increased? The slope would stay the same & the budget constraint would shift out parallel to the original one. Suppose in our example with income of 24 & prices of 3 & 4, income increased to 36. Our new y-intercept will be 36/4 =9 & the new X-intercept will be 36/3=12. (8, 0) (12, 0) X
We have the intercept is I /p 2, & the slope is –p 1/p 2. Y (0, 9) (0, 6) 0 What if income increased? The slope would stay the same & the budget constraint would shift out parallel to the original one. Suppose in our example with income of 24 & prices of 3 & 4, income increased to 36. Our new y-intercept will be 36/4 =9 & the new X-intercept will be 36/3=12. (8, 0) (12, 0) X
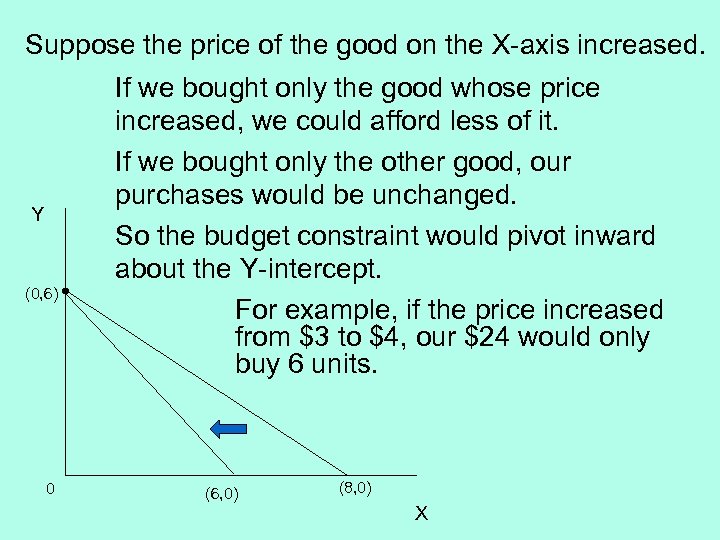 Suppose the price of the good on the X-axis increased. Y (0, 6) 0 If we bought only the good whose price increased, we could afford less of it. If we bought only the other good, our purchases would be unchanged. So the budget constraint would pivot inward about the Y-intercept. For example, if the price increased from $3 to $4, our $24 would only buy 6 units. (6, 0) (8, 0) X
Suppose the price of the good on the X-axis increased. Y (0, 6) 0 If we bought only the good whose price increased, we could afford less of it. If we bought only the other good, our purchases would be unchanged. So the budget constraint would pivot inward about the Y-intercept. For example, if the price increased from $3 to $4, our $24 would only buy 6 units. (6, 0) (8, 0) X
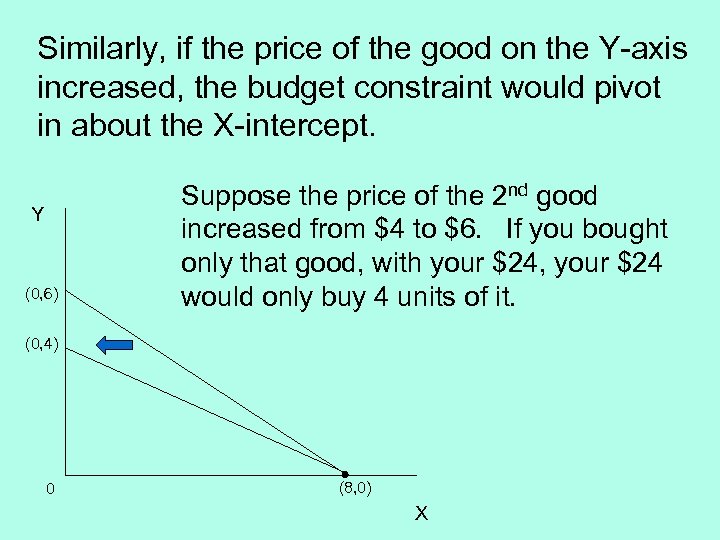 Similarly, if the price of the good on the Y-axis increased, the budget constraint would pivot in about the X-intercept. Y (0, 6) Suppose the price of the 2 nd good increased from $4 to $6. If you bought only that good, with your $24, your $24 would only buy 4 units of it. (0, 4) 0 (8, 0) X
Similarly, if the price of the good on the Y-axis increased, the budget constraint would pivot in about the X-intercept. Y (0, 6) Suppose the price of the 2 nd good increased from $4 to $6. If you bought only that good, with your $24, your $24 would only buy 4 units of it. (0, 4) 0 (8, 0) X
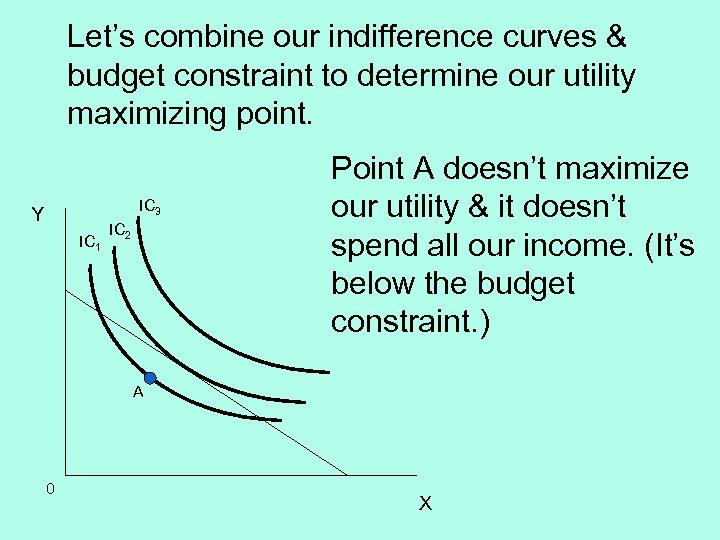 Let’s combine our indifference curves & budget constraint to determine our utility maximizing point. IC 3 Y IC 1 IC 2 Point A doesn’t maximize our utility & it doesn’t spend all our income. (It’s below the budget constraint. ) A 0 X
Let’s combine our indifference curves & budget constraint to determine our utility maximizing point. IC 3 Y IC 1 IC 2 Point A doesn’t maximize our utility & it doesn’t spend all our income. (It’s below the budget constraint. ) A 0 X
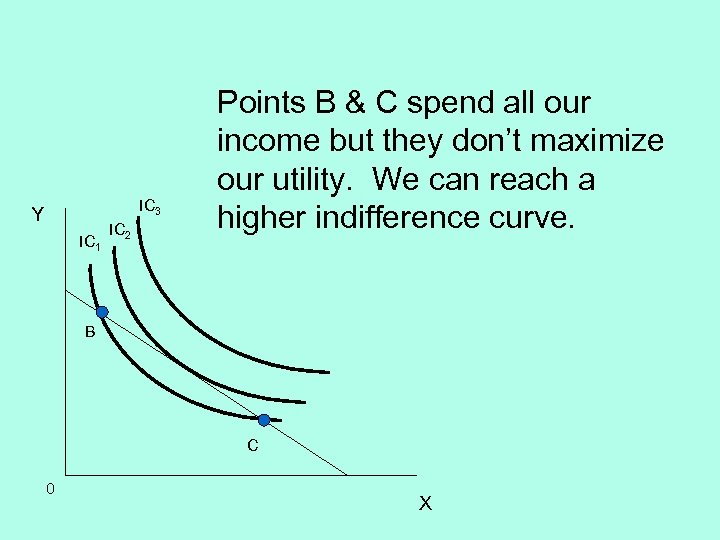 IC 3 Y IC 1 IC 2 Points B & C spend all our income but they don’t maximize our utility. We can reach a higher indifference curve. B C 0 X
IC 3 Y IC 1 IC 2 Points B & C spend all our income but they don’t maximize our utility. We can reach a higher indifference curve. B C 0 X
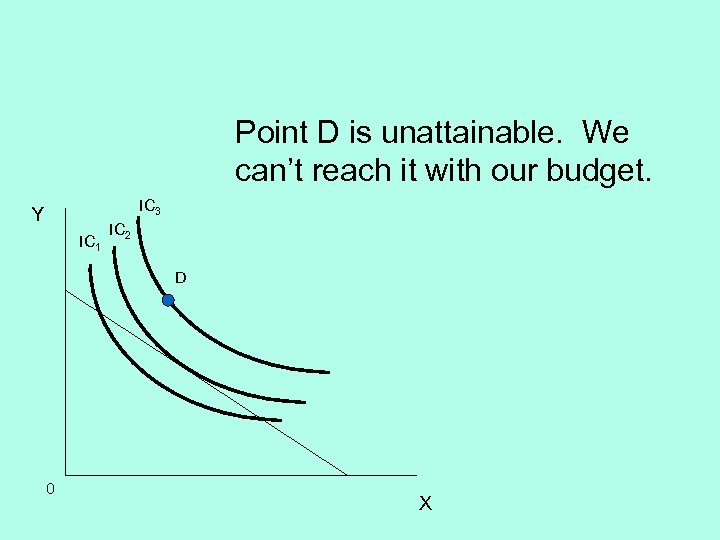 Point D is unattainable. We can’t reach it with our budget. IC 3 Y IC 1 IC 2 D 0 X
Point D is unattainable. We can’t reach it with our budget. IC 3 Y IC 1 IC 2 D 0 X
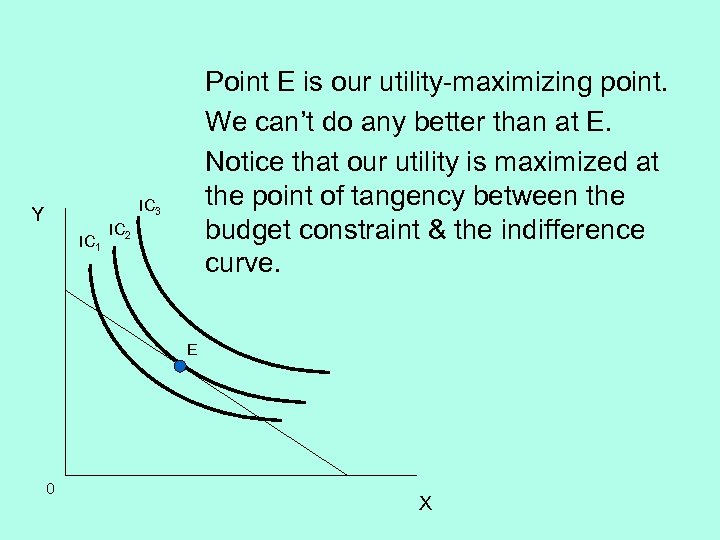 Point E is our utility-maximizing point. We can’t do any better than at E. Notice that our utility is maximized at the point of tangency between the budget constraint & the indifference curve. IC 3 Y IC 1 IC 2 E 0 X
Point E is our utility-maximizing point. We can’t do any better than at E. Notice that our utility is maximized at the point of tangency between the budget constraint & the indifference curve. IC 3 Y IC 1 IC 2 E 0 X
 Recall from Principles of Microeconomics, to maximize your utility, you should purchase goods so that the marginal utility per dollar is the same for all goods. If there were just two goods, that means that MU 1/P 1 = MU 2/P 2 Multiplying both sides by P 1/MU 2, we have MU 1/MU 2 = P 1/P 2. The expression on the right is the negative of the slope of the budget constraint. The expression on the left is the negative of the slope of the indifference curve. So the slope of the indifference curve must be equal to the slope of the budget constraint. If at a particular point, two functions have the same slope, they are tangent to each other. That means your utility-maximizing consumption levels are where your indifference curve is tangent to the budget constraint. This is the same conclusion we reached using our graph.
Recall from Principles of Microeconomics, to maximize your utility, you should purchase goods so that the marginal utility per dollar is the same for all goods. If there were just two goods, that means that MU 1/P 1 = MU 2/P 2 Multiplying both sides by P 1/MU 2, we have MU 1/MU 2 = P 1/P 2. The expression on the right is the negative of the slope of the budget constraint. The expression on the left is the negative of the slope of the indifference curve. So the slope of the indifference curve must be equal to the slope of the budget constraint. If at a particular point, two functions have the same slope, they are tangent to each other. That means your utility-maximizing consumption levels are where your indifference curve is tangent to the budget constraint. This is the same conclusion we reached using our graph.
 Example: If TU = 10 X + 24 Y – 0. 5 X 2 – 0. 5 Y 2, the prices of the two goods are 2 and 6, and we have $44, how much should you consume of each good? Taking the derivatives of TU we have MU 1 = 10 – X and MU 2 = 24 – Y Since MU 1/MU 2 = P 1/P 2 , we have (10 – X) / (24 – Y) = 2 / 6 , or 60 – 6 X = 48 – 2 Y , or 6 X – 2 Y = 12. This an equation with two unknowns. Our budget constraint provides us with a 2 nd equation. Combining the two equations, we can solve for X & Y. The budget constraint is 2 X + 6 Y = 44.
Example: If TU = 10 X + 24 Y – 0. 5 X 2 – 0. 5 Y 2, the prices of the two goods are 2 and 6, and we have $44, how much should you consume of each good? Taking the derivatives of TU we have MU 1 = 10 – X and MU 2 = 24 – Y Since MU 1/MU 2 = P 1/P 2 , we have (10 – X) / (24 – Y) = 2 / 6 , or 60 – 6 X = 48 – 2 Y , or 6 X – 2 Y = 12. This an equation with two unknowns. Our budget constraint provides us with a 2 nd equation. Combining the two equations, we can solve for X & Y. The budget constraint is 2 X + 6 Y = 44.
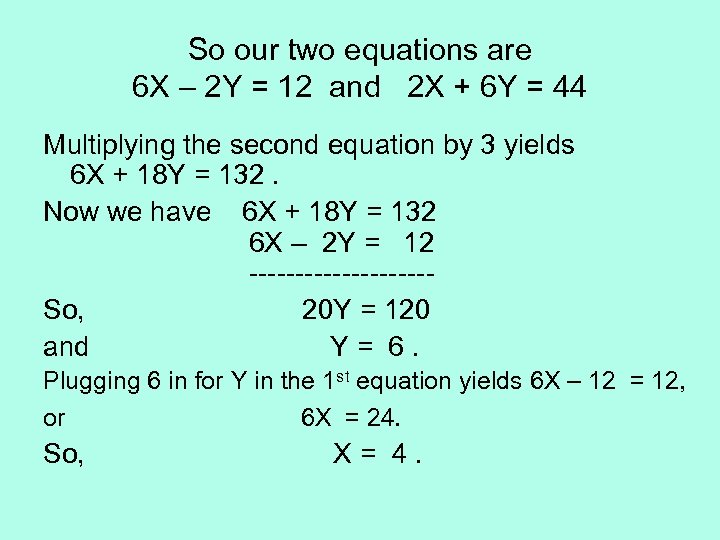 So our two equations are 6 X – 2 Y = 12 and 2 X + 6 Y = 44 Multiplying the second equation by 3 yields 6 X + 18 Y = 132. Now we have 6 X + 18 Y = 132 6 X – 2 Y = 12 ----------So, 20 Y = 120 and Y= 6. Plugging 6 in for Y in the 1 st equation yields 6 X – 12 = 12, or 6 X = 24. So, X= 4.
So our two equations are 6 X – 2 Y = 12 and 2 X + 6 Y = 44 Multiplying the second equation by 3 yields 6 X + 18 Y = 132. Now we have 6 X + 18 Y = 132 6 X – 2 Y = 12 ----------So, 20 Y = 120 and Y= 6. Plugging 6 in for Y in the 1 st equation yields 6 X – 12 = 12, or 6 X = 24. So, X= 4.
 Let’s see if all this works. We had $44, the prices were 2 & 6, and MU 1 = 10 – X & MU 2 = 24 – Y. We bought 4 units of the 1 st good & 6 of the 2 nd good. First, did we spend exactly what we had? We spent (2)(4) + (6)(6) = 8 + 36 = 44 Good. Is the marginal utility per dollar the same for both goods? For the 1 st good: MU 1/P 1 = (10 – X)/2 = (10 -4)/2 = 3 For the 2 nd good: MU 2/P 2 = (24 – Y)/6 = (24 -6)/6 = 3 So they’re equal and things look fine.
Let’s see if all this works. We had $44, the prices were 2 & 6, and MU 1 = 10 – X & MU 2 = 24 – Y. We bought 4 units of the 1 st good & 6 of the 2 nd good. First, did we spend exactly what we had? We spent (2)(4) + (6)(6) = 8 + 36 = 44 Good. Is the marginal utility per dollar the same for both goods? For the 1 st good: MU 1/P 1 = (10 – X)/2 = (10 -4)/2 = 3 For the 2 nd good: MU 2/P 2 = (24 – Y)/6 = (24 -6)/6 = 3 So they’re equal and things look fine.
 What happens to consumption when income rises? For normal goods, consumption increases. For inferior goods, consumption decreases. What does this look like on our graph?
What happens to consumption when income rises? For normal goods, consumption increases. For inferior goods, consumption decreases. What does this look like on our graph?
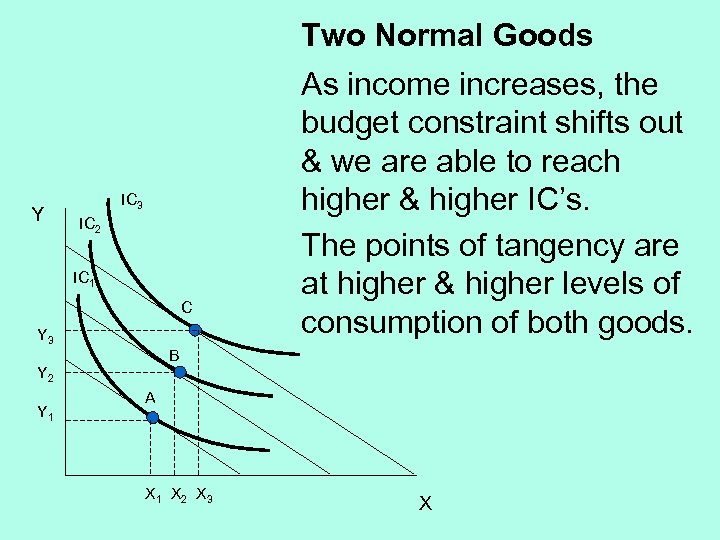 Two Normal Goods Y IC 3 IC 2 IC 1 C Y 3 B Y 2 Y 1 As income increases, the budget constraint shifts out & we are able to reach higher & higher IC’s. The points of tangency are at higher & higher levels of consumption of both goods. A X 1 X 2 X 3 X
Two Normal Goods Y IC 3 IC 2 IC 1 C Y 3 B Y 2 Y 1 As income increases, the budget constraint shifts out & we are able to reach higher & higher IC’s. The points of tangency are at higher & higher levels of consumption of both goods. A X 1 X 2 X 3 X
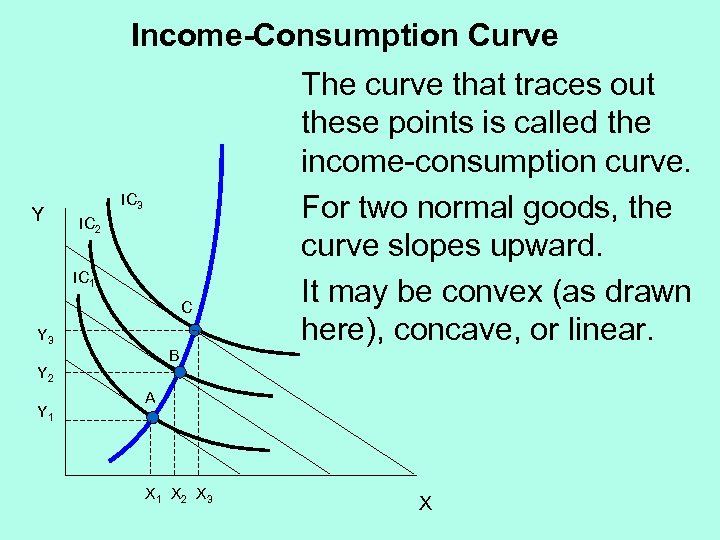 Income-Consumption Curve Y IC 3 IC 2 IC 1 C Y 3 B Y 2 Y 1 The curve that traces out these points is called the income-consumption curve. For two normal goods, the curve slopes upward. It may be convex (as drawn here), concave, or linear. A X 1 X 2 X 3 X
Income-Consumption Curve Y IC 3 IC 2 IC 1 C Y 3 B Y 2 Y 1 The curve that traces out these points is called the income-consumption curve. For two normal goods, the curve slopes upward. It may be convex (as drawn here), concave, or linear. A X 1 X 2 X 3 X
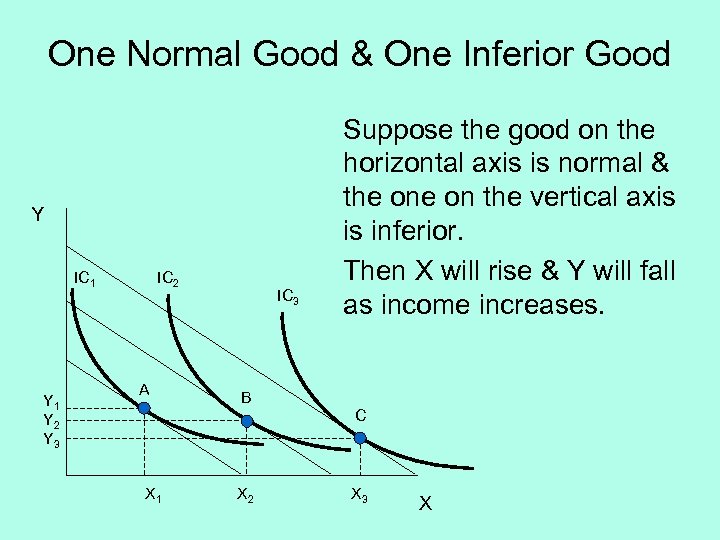 One Normal Good & One Inferior Good Y IC 1 Y 2 Y 3 IC 2 A IC 3 Suppose the good on the horizontal axis is normal & the on the vertical axis is inferior. Then X will rise & Y will fall as income increases. B C X 1 X 2 X 3 X
One Normal Good & One Inferior Good Y IC 1 Y 2 Y 3 IC 2 A IC 3 Suppose the good on the horizontal axis is normal & the on the vertical axis is inferior. Then X will rise & Y will fall as income increases. B C X 1 X 2 X 3 X
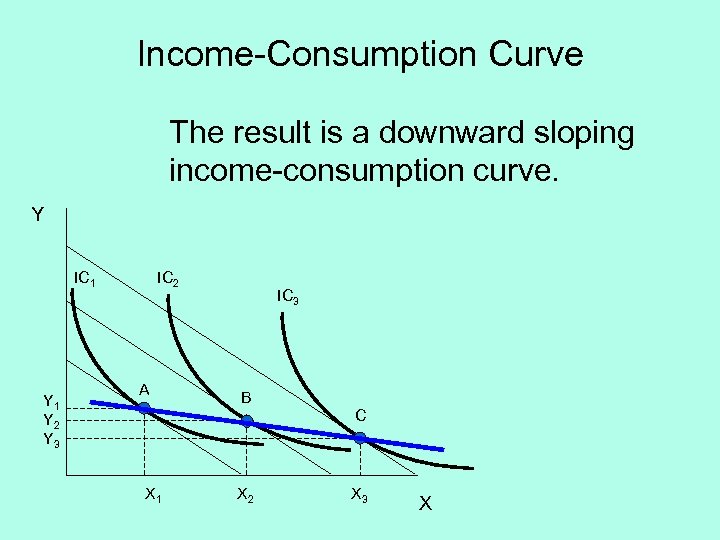 Income-Consumption Curve The result is a downward sloping income-consumption curve. Y IC 1 Y 2 Y 3 IC 2 A IC 3 B C X 1 X 2 X 3 X
Income-Consumption Curve The result is a downward sloping income-consumption curve. Y IC 1 Y 2 Y 3 IC 2 A IC 3 B C X 1 X 2 X 3 X
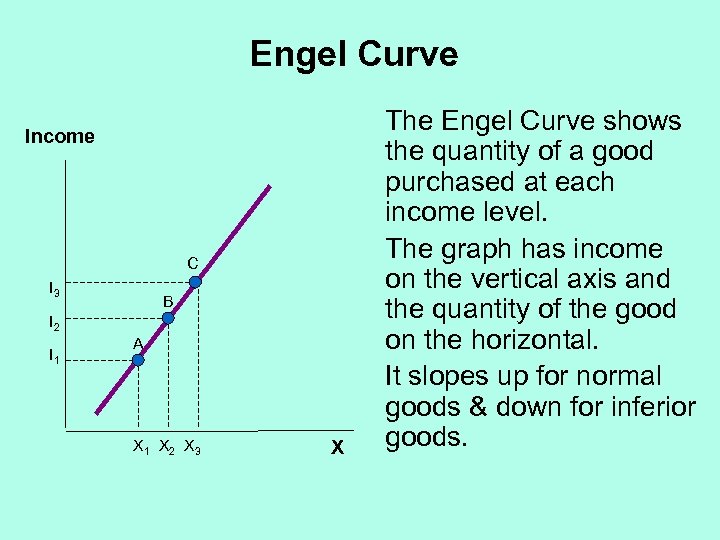 Engel Curve Income C I 3 B I 2 I 1 A X 1 X 2 X 3 X The Engel Curve shows the quantity of a good purchased at each income level. The graph has income on the vertical axis and the quantity of the good on the horizontal. It slopes up for normal goods & down for inferior goods.
Engel Curve Income C I 3 B I 2 I 1 A X 1 X 2 X 3 X The Engel Curve shows the quantity of a good purchased at each income level. The graph has income on the vertical axis and the quantity of the good on the horizontal. It slopes up for normal goods & down for inferior goods.
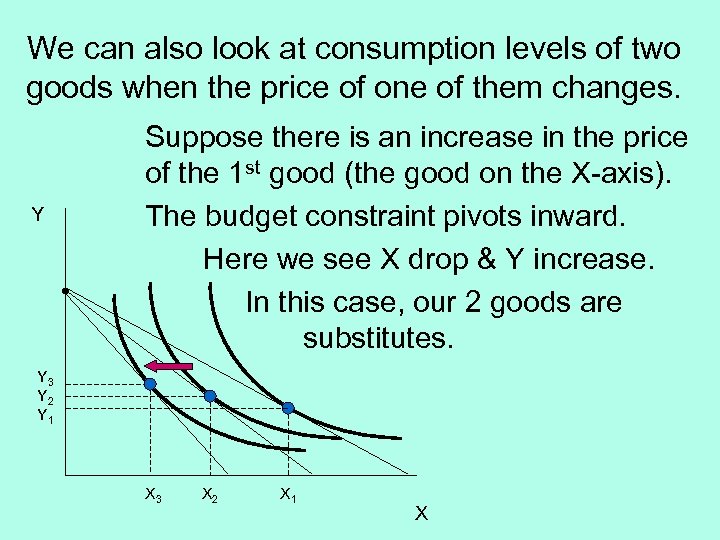 We can also look at consumption levels of two goods when the price of one of them changes. Y Suppose there is an increase in the price of the 1 st good (the good on the X-axis). The budget constraint pivots inward. Here we see X drop & Y increase. In this case, our 2 goods are substitutes. Y 3 Y 2 Y 1 X 3 X 2 X 1 X
We can also look at consumption levels of two goods when the price of one of them changes. Y Suppose there is an increase in the price of the 1 st good (the good on the X-axis). The budget constraint pivots inward. Here we see X drop & Y increase. In this case, our 2 goods are substitutes. Y 3 Y 2 Y 1 X 3 X 2 X 1 X
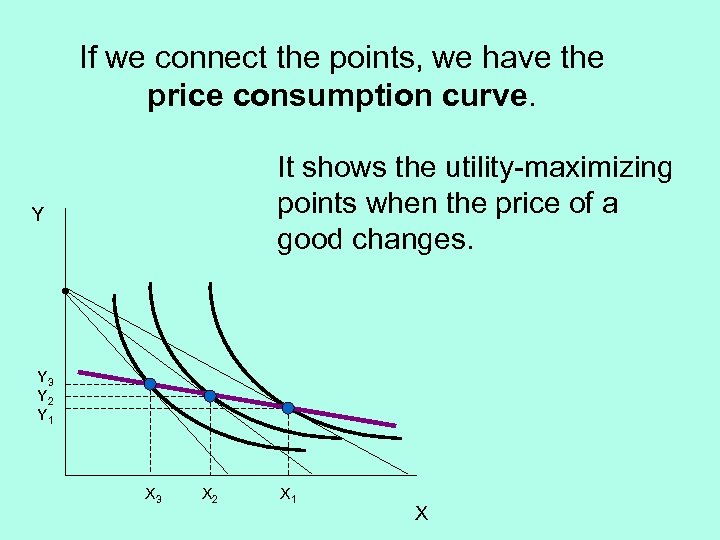 If we connect the points, we have the price consumption curve. It shows the utility-maximizing points when the price of a good changes. Y Y 3 Y 2 Y 1 X 3 X 2 X 1 X
If we connect the points, we have the price consumption curve. It shows the utility-maximizing points when the price of a good changes. Y Y 3 Y 2 Y 1 X 3 X 2 X 1 X
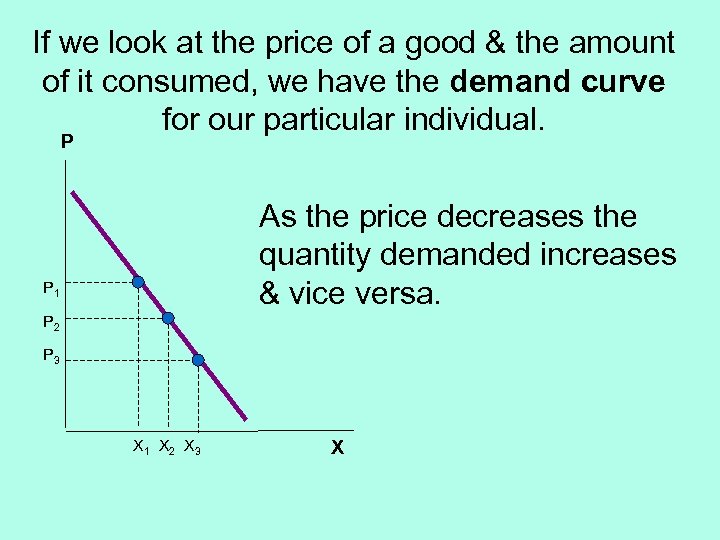 If we look at the price of a good & the amount of it consumed, we have the demand curve for our particular individual. P As the price decreases the quantity demanded increases & vice versa. P 1 P 2 P 3 X 1 X 2 X 3 X
If we look at the price of a good & the amount of it consumed, we have the demand curve for our particular individual. P As the price decreases the quantity demanded increases & vice versa. P 1 P 2 P 3 X 1 X 2 X 3 X
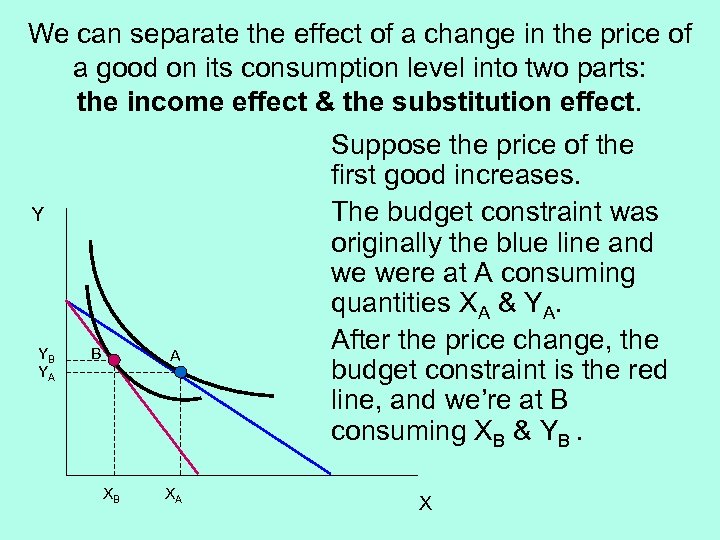 We can separate the effect of a change in the price of a good on its consumption level into two parts: the income effect & the substitution effect. Y YB YA B A XB XA Suppose the price of the first good increases. The budget constraint was originally the blue line and we were at A consuming quantities XA & YA. After the price change, the budget constraint is the red line, and we’re at B consuming XB & YB. X
We can separate the effect of a change in the price of a good on its consumption level into two parts: the income effect & the substitution effect. Y YB YA B A XB XA Suppose the price of the first good increases. The budget constraint was originally the blue line and we were at A consuming quantities XA & YA. After the price change, the budget constraint is the red line, and we’re at B consuming XB & YB. X
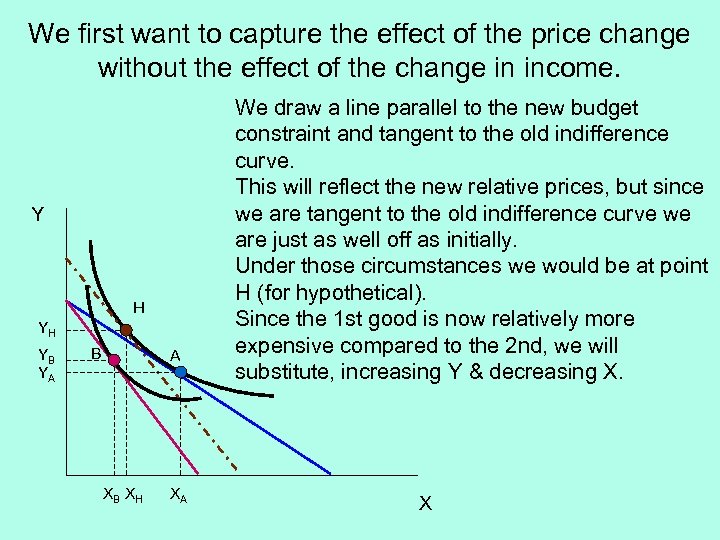 We first want to capture the effect of the price change without the effect of the change in income. Y H YH YB YA B A XB X H XA We draw a line parallel to the new budget constraint and tangent to the old indifference curve. This will reflect the new relative prices, but since we are tangent to the old indifference curve we are just as well off as initially. Under those circumstances we would be at point H (for hypothetical). Since the 1 st good is now relatively more expensive compared to the 2 nd, we will substitute, increasing Y & decreasing X. X
We first want to capture the effect of the price change without the effect of the change in income. Y H YH YB YA B A XB X H XA We draw a line parallel to the new budget constraint and tangent to the old indifference curve. This will reflect the new relative prices, but since we are tangent to the old indifference curve we are just as well off as initially. Under those circumstances we would be at point H (for hypothetical). Since the 1 st good is now relatively more expensive compared to the 2 nd, we will substitute, increasing Y & decreasing X. X
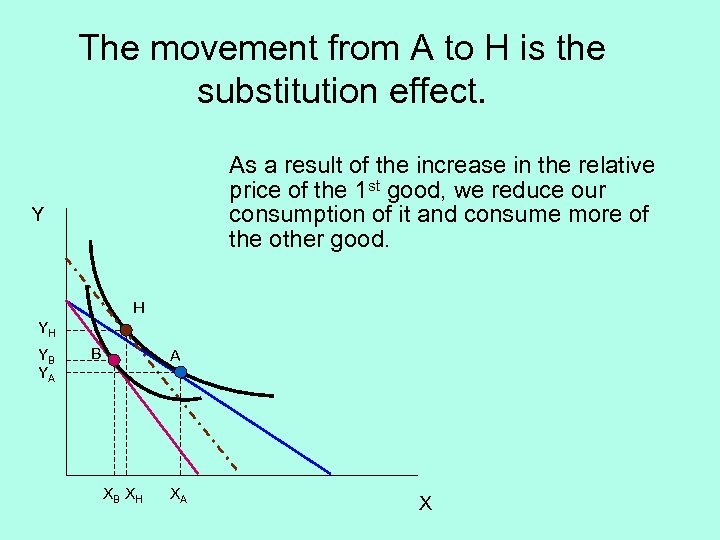 The movement from A to H is the substitution effect. As a result of the increase in the relative price of the 1 st good, we reduce our consumption of it and consume more of the other good. Y H YH YB YA B A XB X H XA X
The movement from A to H is the substitution effect. As a result of the increase in the relative price of the 1 st good, we reduce our consumption of it and consume more of the other good. Y H YH YB YA B A XB X H XA X
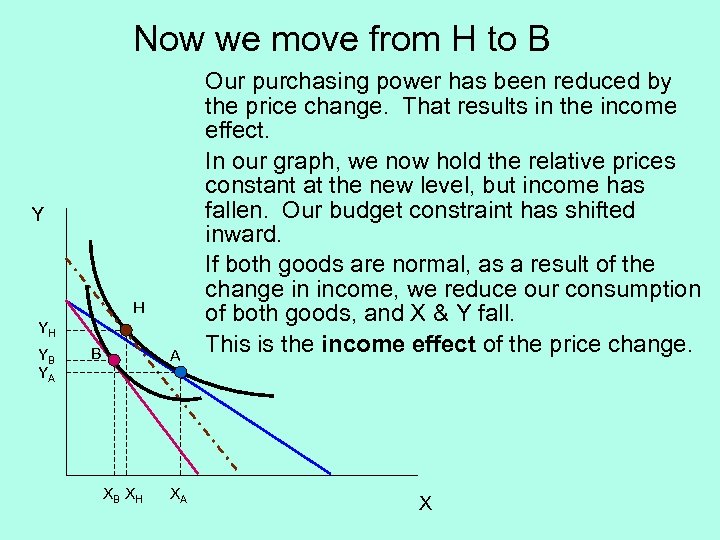 Now we move from H to B Y H YH YB YA B A XB X H XA Our purchasing power has been reduced by the price change. That results in the income effect. In our graph, we now hold the relative prices constant at the new level, but income has fallen. Our budget constraint has shifted inward. If both goods are normal, as a result of the change in income, we reduce our consumption of both goods, and X & Y fall. This is the income effect of the price change. X
Now we move from H to B Y H YH YB YA B A XB X H XA Our purchasing power has been reduced by the price change. That results in the income effect. In our graph, we now hold the relative prices constant at the new level, but income has fallen. Our budget constraint has shifted inward. If both goods are normal, as a result of the change in income, we reduce our consumption of both goods, and X & Y fall. This is the income effect of the price change. X
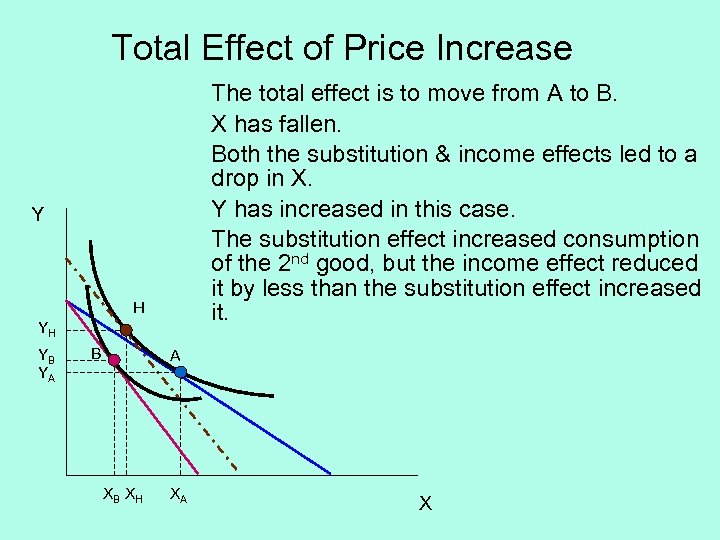 Total Effect of Price Increase The total effect is to move from A to B. X has fallen. Both the substitution & income effects led to a drop in X. Y has increased in this case. The substitution effect increased consumption of the 2 nd good, but the income effect reduced it by less than the substitution effect increased it. Y H YH YB YA B A XB X H XA X
Total Effect of Price Increase The total effect is to move from A to B. X has fallen. Both the substitution & income effects led to a drop in X. Y has increased in this case. The substitution effect increased consumption of the 2 nd good, but the income effect reduced it by less than the substitution effect increased it. Y H YH YB YA B A XB X H XA X
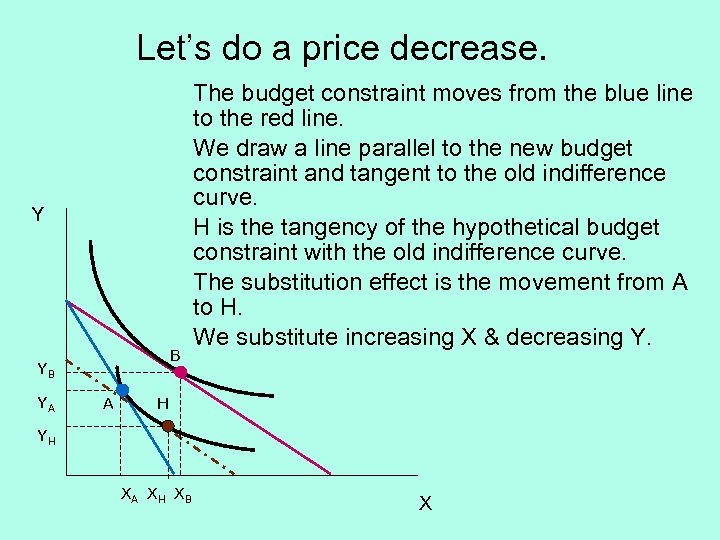 Let’s do a price decrease. Y B YB YA A The budget constraint moves from the blue line to the red line. We draw a line parallel to the new budget constraint and tangent to the old indifference curve. H is the tangency of the hypothetical budget constraint with the old indifference curve. The substitution effect is the movement from A to H. We substitute increasing X & decreasing Y. H YH XA X H X B X
Let’s do a price decrease. Y B YB YA A The budget constraint moves from the blue line to the red line. We draw a line parallel to the new budget constraint and tangent to the old indifference curve. H is the tangency of the hypothetical budget constraint with the old indifference curve. The substitution effect is the movement from A to H. We substitute increasing X & decreasing Y. H YH XA X H X B X
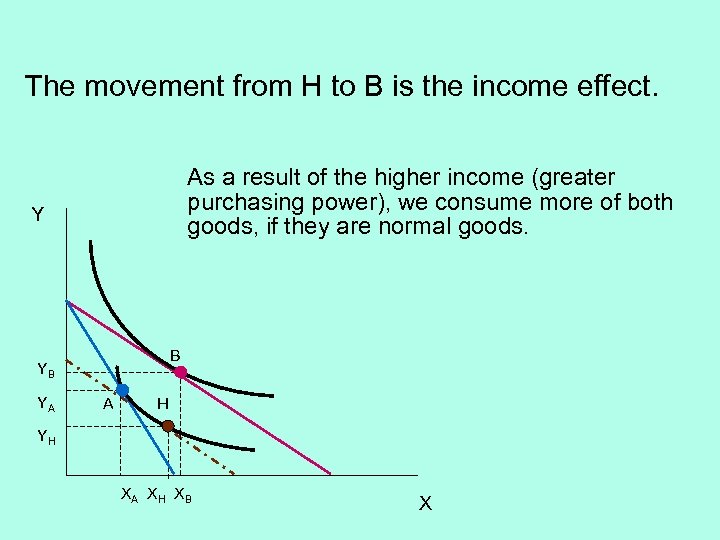 The movement from H to B is the income effect. As a result of the higher income (greater purchasing power), we consume more of both goods, if they are normal goods. Y B YB YA A H YH XA X H X B X
The movement from H to B is the income effect. As a result of the higher income (greater purchasing power), we consume more of both goods, if they are normal goods. Y B YB YA A H YH XA X H X B X
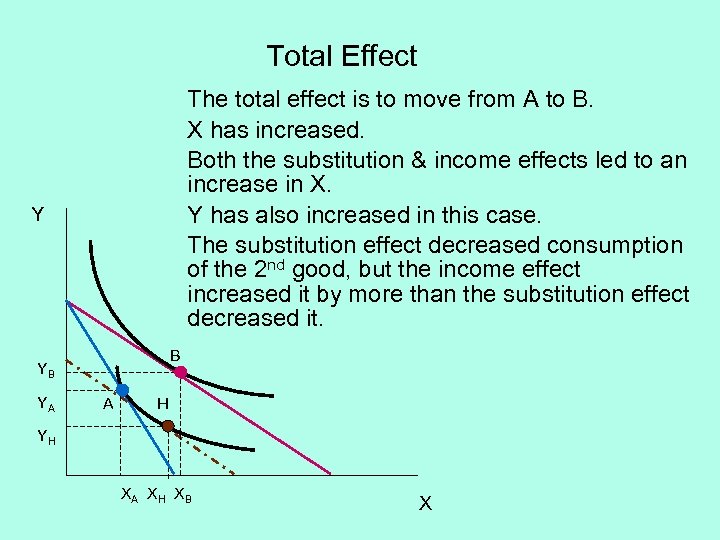 Total Effect The total effect is to move from A to B. X has increased. Both the substitution & income effects led to an increase in X. Y has also increased in this case. The substitution effect decreased consumption of the 2 nd good, but the income effect increased it by more than the substitution effect decreased it. Y B YB YA A H YH XA X H X B X
Total Effect The total effect is to move from A to B. X has increased. Both the substitution & income effects led to an increase in X. Y has also increased in this case. The substitution effect decreased consumption of the 2 nd good, but the income effect increased it by more than the substitution effect decreased it. Y B YB YA A H YH XA X H X B X
 Income and Substitution Effects, in words The income effect is the result of the change in purchasing power. If the price of a normal good increases, you feel poorer, and the income effect is to consume less. If the price of a normal good decreases, you feel richer, and the income effect is to consume more. The substitution effect is the result of a change in relative prices. If the price of a good increases, the substitution effect is to consume less of it & more of the other goods that are now relatively cheaper. If the price decreases, the substitution effect is to consume more of it & less of the goods that are now relatively more expensive.
Income and Substitution Effects, in words The income effect is the result of the change in purchasing power. If the price of a normal good increases, you feel poorer, and the income effect is to consume less. If the price of a normal good decreases, you feel richer, and the income effect is to consume more. The substitution effect is the result of a change in relative prices. If the price of a good increases, the substitution effect is to consume less of it & more of the other goods that are now relatively cheaper. If the price decreases, the substitution effect is to consume more of it & less of the goods that are now relatively more expensive.
 What if the price changed of an inferior good? The substitution effect would be the same but the income effect would be the opposite.
What if the price changed of an inferior good? The substitution effect would be the same but the income effect would be the opposite.
 Price increase for an inferior good Income effect: Your purchasing power has decreased. You feel poorer. So you consume more of the inferior good. Substitution effect: The good is now relatively more expensive than other goods, so you consume less of it and more of other goods. Notice the IE & SE are in opposite directions in this case. If the SE is larger than the IE, you will consume less of the good. If the IE is larger than the SE, you will consume more of the good.
Price increase for an inferior good Income effect: Your purchasing power has decreased. You feel poorer. So you consume more of the inferior good. Substitution effect: The good is now relatively more expensive than other goods, so you consume less of it and more of other goods. Notice the IE & SE are in opposite directions in this case. If the SE is larger than the IE, you will consume less of the good. If the IE is larger than the SE, you will consume more of the good.
 An inferior good for which the IE is larger than the SE is called a Giffen good. It is a good for which consumption rises when the price increases, and consumption falls when the price decreases.
An inferior good for which the IE is larger than the SE is called a Giffen good. It is a good for which consumption rises when the price increases, and consumption falls when the price decreases.
 Price decrease for an inferior good Income effect: Your purchasing power has increased. You feel richer. So you consume less of the inferior good. Substitution effect: The good is now relatively more cheaper than other goods, so you consume more of it and less of other goods. Again the IE & SE are in opposite directions in this case. If the SE is larger than the IE, you will consume more of the good. If the IE is larger than the SE, you will consume less of the good.
Price decrease for an inferior good Income effect: Your purchasing power has increased. You feel richer. So you consume less of the inferior good. Substitution effect: The good is now relatively more cheaper than other goods, so you consume more of it and less of other goods. Again the IE & SE are in opposite directions in this case. If the SE is larger than the IE, you will consume more of the good. If the IE is larger than the SE, you will consume less of the good.
 We previously looked at the demand curve for individuals. How do we get the market demand curve from the demand curve for individuals? We just horizontally sum up the individual demand curves.
We previously looked at the demand curve for individuals. How do we get the market demand curve from the demand curve for individuals? We just horizontally sum up the individual demand curves.
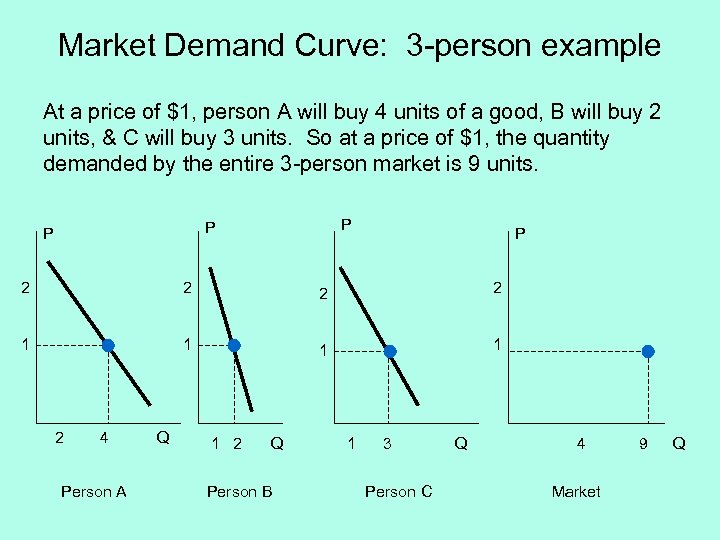 Market Demand Curve: 3 -person example At a price of $1, person A will buy 4 units of a good, B will buy 2 units, & C will buy 3 units. So at a price of $1, the quantity demanded by the entire 3 -person market is 9 units. P P 2 2 1 1 2 4 Person A Q 1 2 Q Person B 1 3 Person C Q 4 Market 9 Q
Market Demand Curve: 3 -person example At a price of $1, person A will buy 4 units of a good, B will buy 2 units, & C will buy 3 units. So at a price of $1, the quantity demanded by the entire 3 -person market is 9 units. P P 2 2 1 1 2 4 Person A Q 1 2 Q Person B 1 3 Person C Q 4 Market 9 Q
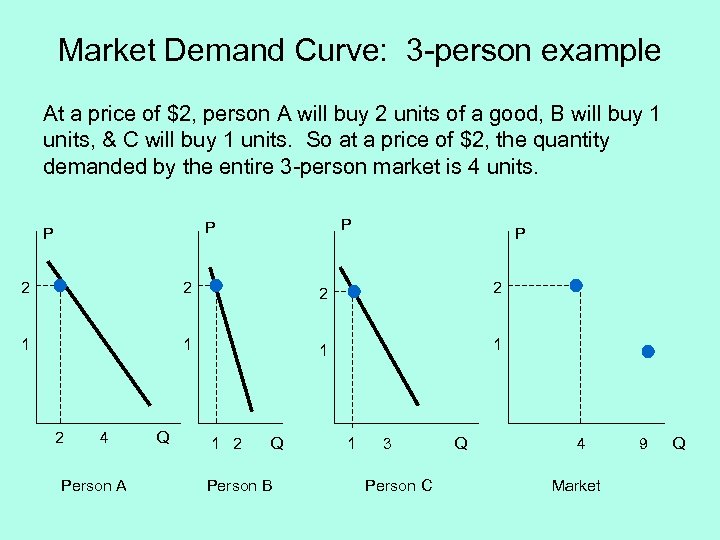 Market Demand Curve: 3 -person example At a price of $2, person A will buy 2 units of a good, B will buy 1 units, & C will buy 1 units. So at a price of $2, the quantity demanded by the entire 3 -person market is 4 units. P P 2 2 1 1 2 4 Person A Q 1 2 Q Person B 1 3 Person C Q 4 Market 9 Q
Market Demand Curve: 3 -person example At a price of $2, person A will buy 2 units of a good, B will buy 1 units, & C will buy 1 units. So at a price of $2, the quantity demanded by the entire 3 -person market is 4 units. P P 2 2 1 1 2 4 Person A Q 1 2 Q Person B 1 3 Person C Q 4 Market 9 Q
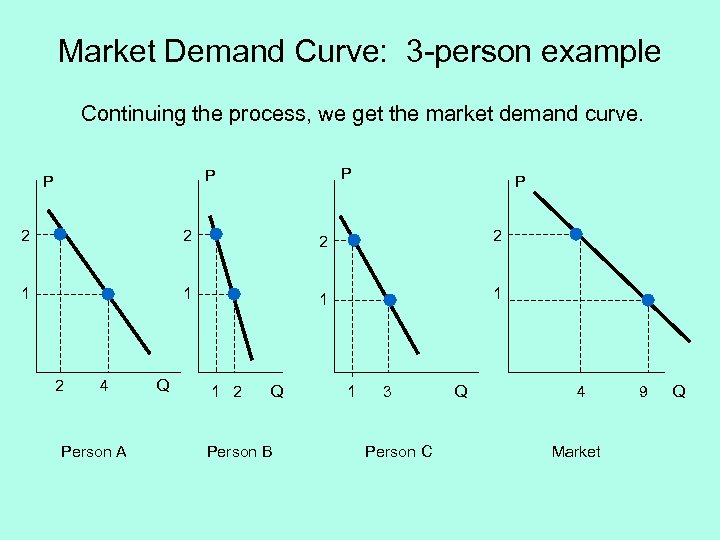 Market Demand Curve: 3 -person example Continuing the process, we get the market demand curve. P P 2 2 1 1 2 4 Person A Q 1 2 Q Person B 1 3 Person C Q 4 Market 9 Q
Market Demand Curve: 3 -person example Continuing the process, we get the market demand curve. P P 2 2 1 1 2 4 Person A Q 1 2 Q Person B 1 3 Person C Q 4 Market 9 Q
 The Demand for a product can be expressed as a function of 1. 2. its price (changes in which lead to movements along the demand curve), and other determinants such as income, prices of related goods, & expectations (changes in which lead to shifts of the demand curve). So we have QDX = g(PX, Psubst, Pcomp, Inc. , Expect. ) A particular demand curve QDX = g(PX) shows the relation between the quantity demanded of a product and its price when we hold all the factors constant. This is also sometimes written as P= f(Q).
The Demand for a product can be expressed as a function of 1. 2. its price (changes in which lead to movements along the demand curve), and other determinants such as income, prices of related goods, & expectations (changes in which lead to shifts of the demand curve). So we have QDX = g(PX, Psubst, Pcomp, Inc. , Expect. ) A particular demand curve QDX = g(PX) shows the relation between the quantity demanded of a product and its price when we hold all the factors constant. This is also sometimes written as P= f(Q).
 Total Revenue TR = PQ
Total Revenue TR = PQ
 Average Revenue total revenue per unit of output AR = TR / Q = (PQ) / Q =P AR & P are the same function of Q.
Average Revenue total revenue per unit of output AR = TR / Q = (PQ) / Q =P AR & P are the same function of Q.
 Marginal Revenue The additional revenue associated with an additional unit of output MR = d. TR / d. Q
Marginal Revenue The additional revenue associated with an additional unit of output MR = d. TR / d. Q
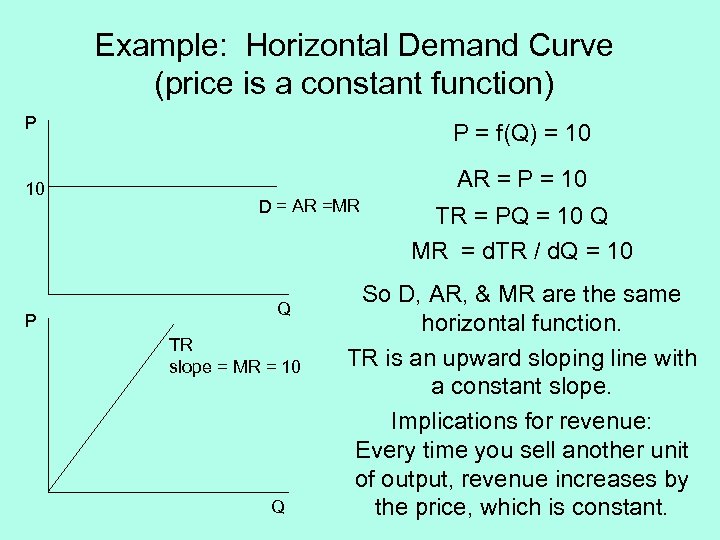 Example: Horizontal Demand Curve (price is a constant function) P 10 P P = f(Q) = 10 AR = P = 10 D = AR =MR Q TR slope = MR = 10 Q TR = PQ = 10 Q MR = d. TR / d. Q = 10 So D, AR, & MR are the same horizontal function. TR is an upward sloping line with a constant slope. Implications for revenue: Every time you sell another unit of output, revenue increases by the price, which is constant.
Example: Horizontal Demand Curve (price is a constant function) P 10 P P = f(Q) = 10 AR = P = 10 D = AR =MR Q TR slope = MR = 10 Q TR = PQ = 10 Q MR = d. TR / d. Q = 10 So D, AR, & MR are the same horizontal function. TR is an upward sloping line with a constant slope. Implications for revenue: Every time you sell another unit of output, revenue increases by the price, which is constant.
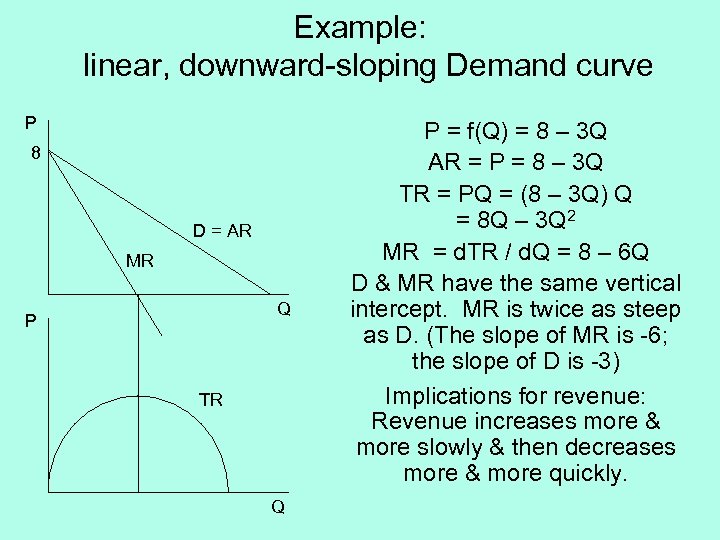 Example: linear, downward-sloping Demand curve P 8 D = AR MR Q P TR Q P = f(Q) = 8 – 3 Q AR = P = 8 – 3 Q TR = PQ = (8 – 3 Q) Q = 8 Q – 3 Q 2 MR = d. TR / d. Q = 8 – 6 Q D & MR have the same vertical intercept. MR is twice as steep as D. (The slope of MR is -6; the slope of D is -3) Implications for revenue: Revenue increases more & more slowly & then decreases more & more quickly.
Example: linear, downward-sloping Demand curve P 8 D = AR MR Q P TR Q P = f(Q) = 8 – 3 Q AR = P = 8 – 3 Q TR = PQ = (8 – 3 Q) Q = 8 Q – 3 Q 2 MR = d. TR / d. Q = 8 – 6 Q D & MR have the same vertical intercept. MR is twice as steep as D. (The slope of MR is -6; the slope of D is -3) Implications for revenue: Revenue increases more & more slowly & then decreases more & more quickly.
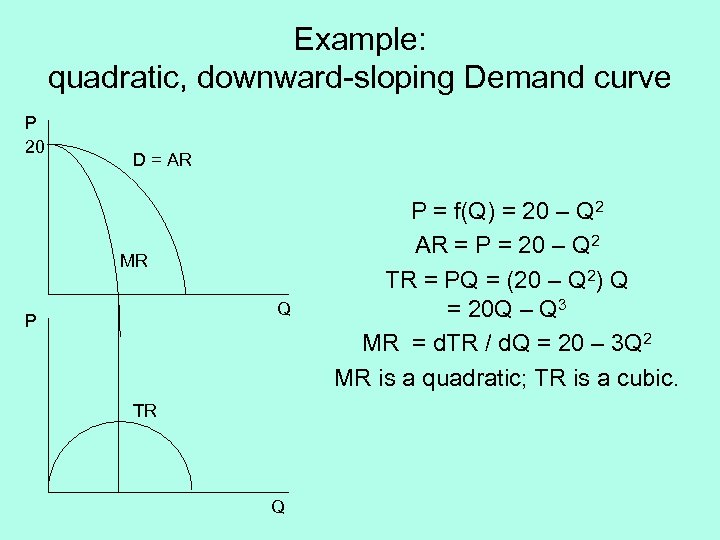 Example: quadratic, downward-sloping Demand curve P 20 D = AR MR Q P TR Q P = f(Q) = 20 – Q 2 AR = P = 20 – Q 2 TR = PQ = (20 – Q 2) Q = 20 Q – Q 3 MR = d. TR / d. Q = 20 – 3 Q 2 MR is a quadratic; TR is a cubic.
Example: quadratic, downward-sloping Demand curve P 20 D = AR MR Q P TR Q P = f(Q) = 20 – Q 2 AR = P = 20 – Q 2 TR = PQ = (20 – Q 2) Q = 20 Q – Q 3 MR = d. TR / d. Q = 20 – 3 Q 2 MR is a quadratic; TR is a cubic.
 Elasticity Responsiveness or sensitivity of one variable to a change in another variable (% change in X) ε = ------------(% change in Y)
Elasticity Responsiveness or sensitivity of one variable to a change in another variable (% change in X) ε = ------------(% change in Y)
 Price Elasticity of Demand (% change in quantity demanded) ε = ------------------------(% change in price)
Price Elasticity of Demand (% change in quantity demanded) ε = ------------------------(% change in price)
 Two methods of calculating elasticity Arc elasticity: measures responsiveness between 2 points Point elasticity: measures responsiveness at a single point for an infinitesimally small change
Two methods of calculating elasticity Arc elasticity: measures responsiveness between 2 points Point elasticity: measures responsiveness at a single point for an infinitesimally small change
![Arc Elasticity ΔQ/(avg Q) [Q 2 – Q 1] / [(Q 1+Q 2)/2] -------- Arc Elasticity ΔQ/(avg Q) [Q 2 – Q 1] / [(Q 1+Q 2)/2] --------](https://present5.com/presentation/cf8816dddd6ec7daf30b766bded36747/image-90.jpg) Arc Elasticity ΔQ/(avg Q) [Q 2 – Q 1] / [(Q 1+Q 2)/2] -------- = ----------------ΔP/(avg P) [P 2 – P 1] / [(P 1+P 2)/2]
Arc Elasticity ΔQ/(avg Q) [Q 2 – Q 1] / [(Q 1+Q 2)/2] -------- = ----------------ΔP/(avg P) [P 2 – P 1] / [(P 1+P 2)/2]
 Arc Elasticity Example Calculate the price elasticity of demand if in response to a increase in price from 9 to 11 dollars, the quantity demanded decreases from 60 to 40 units. P: 9→ 11 Q: 60→ 40 ΔQ/(avg Q) [Q 2 – Q 1] / [(Q 1+Q 2)/2] ε = -----------------------ΔP/(avg P) [P 2 – P 1] / [(P 1+P 2)/2] [40 – 60] / [(60+40)/2] -20 / 50 -0. 4 = --------------- = ------- = -2. 0 [11 – 9] / [(9+11)/2] 2 / 10 0. 2 The negative sign indicates that price & quantity move in opposite directions. The negative sign is sometimes dropped with the understanding that price & quantity are still moving in opposite directions.
Arc Elasticity Example Calculate the price elasticity of demand if in response to a increase in price from 9 to 11 dollars, the quantity demanded decreases from 60 to 40 units. P: 9→ 11 Q: 60→ 40 ΔQ/(avg Q) [Q 2 – Q 1] / [(Q 1+Q 2)/2] ε = -----------------------ΔP/(avg P) [P 2 – P 1] / [(P 1+P 2)/2] [40 – 60] / [(60+40)/2] -20 / 50 -0. 4 = --------------- = ------- = -2. 0 [11 – 9] / [(9+11)/2] 2 / 10 0. 2 The negative sign indicates that price & quantity move in opposite directions. The negative sign is sometimes dropped with the understanding that price & quantity are still moving in opposite directions.
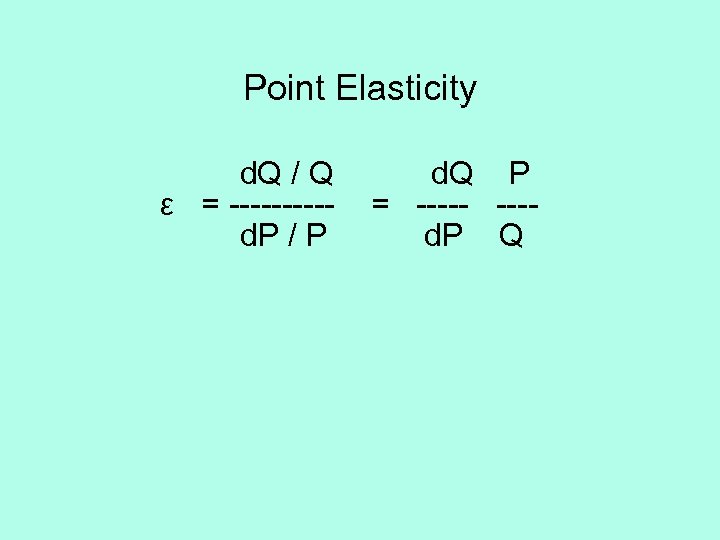 Point Elasticity d. Q / Q ε = -----d. P / P d. Q P = ----- ---d. P Q
Point Elasticity d. Q / Q ε = -----d. P / P d. Q P = ----- ---d. P Q
 Point Elasticity Example If the demand function is Q = 245 – 3. 5 P, find the price elasticity of demand when the price is 10. When P = 10, Q = 245 – 3. 5(10) = 210 The derivative d. Q / d. P = = – 3. 5 d. Q / Q ε = -----d. P / P d. Q P 10 = ----- = - 3. 5 ------ = - 0. 167 d. P Q 210
Point Elasticity Example If the demand function is Q = 245 – 3. 5 P, find the price elasticity of demand when the price is 10. When P = 10, Q = 245 – 3. 5(10) = 210 The derivative d. Q / d. P = = – 3. 5 d. Q / Q ε = -----d. P / P d. Q P 10 = ----- = - 3. 5 ------ = - 0. 167 d. P Q 210
 Categories of Price Elasticity of Demand is elastic if Demand is inelastic if Demand is unit elastic if |ε| > 1 |ε| < 1 |ε| = 1
Categories of Price Elasticity of Demand is elastic if Demand is inelastic if Demand is unit elastic if |ε| > 1 |ε| < 1 |ε| = 1
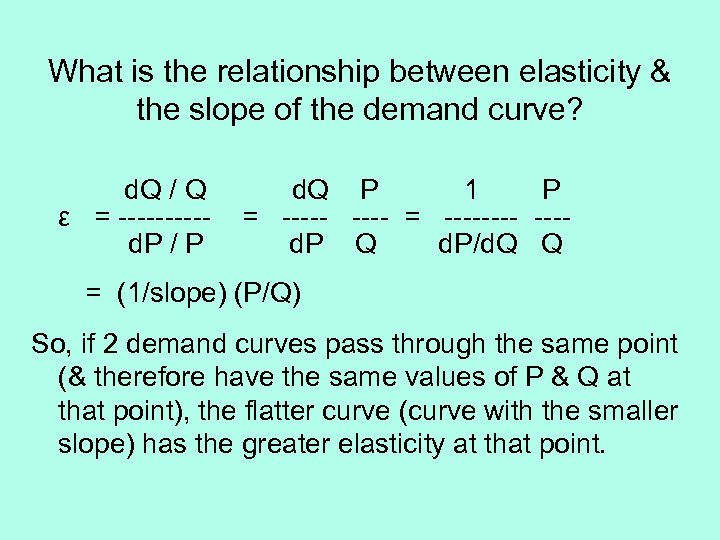 What is the relationship between elasticity & the slope of the demand curve? d. Q / Q ε = -----d. P / P d. Q P 1 P = ----- = ---- ---d. P Q d. P/d. Q Q = (1/slope) (P/Q) So, if 2 demand curves pass through the same point (& therefore have the same values of P & Q at that point), the flatter curve (curve with the smaller slope) has the greater elasticity at that point.
What is the relationship between elasticity & the slope of the demand curve? d. Q / Q ε = -----d. P / P d. Q P 1 P = ----- = ---- ---d. P Q d. P/d. Q Q = (1/slope) (P/Q) So, if 2 demand curves pass through the same point (& therefore have the same values of P & Q at that point), the flatter curve (curve with the smaller slope) has the greater elasticity at that point.
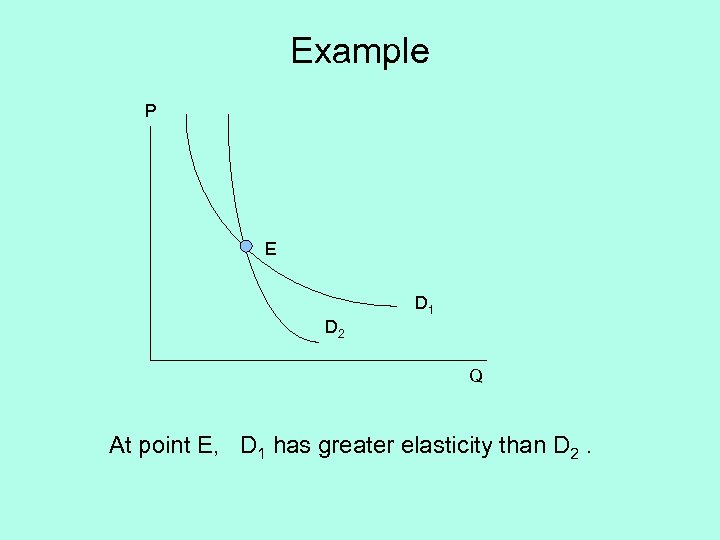 Example P E D 1 D 2 Q At point E, D 1 has greater elasticity than D 2.
Example P E D 1 D 2 Q At point E, D 1 has greater elasticity than D 2.
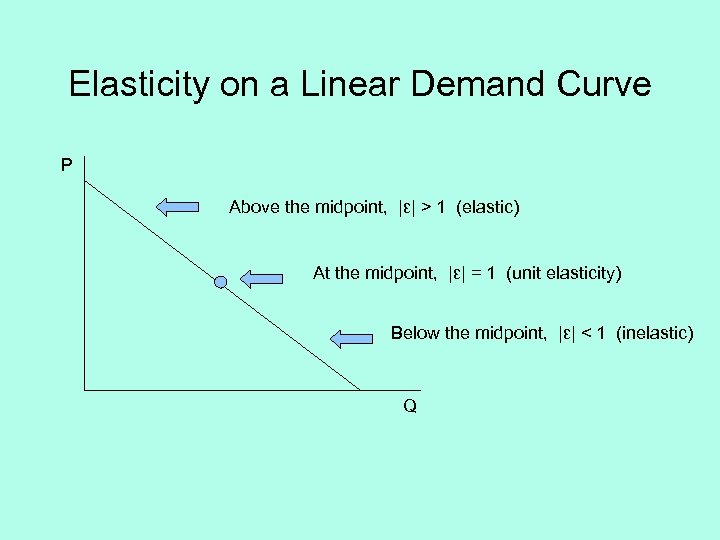 Elasticity on a Linear Demand Curve P Above the midpoint, |ε| > 1 (elastic) At the midpoint, |ε| = 1 (unit elasticity) Below the midpoint, |ε| < 1 (inelastic) Q
Elasticity on a Linear Demand Curve P Above the midpoint, |ε| > 1 (elastic) At the midpoint, |ε| = 1 (unit elasticity) Below the midpoint, |ε| < 1 (inelastic) Q
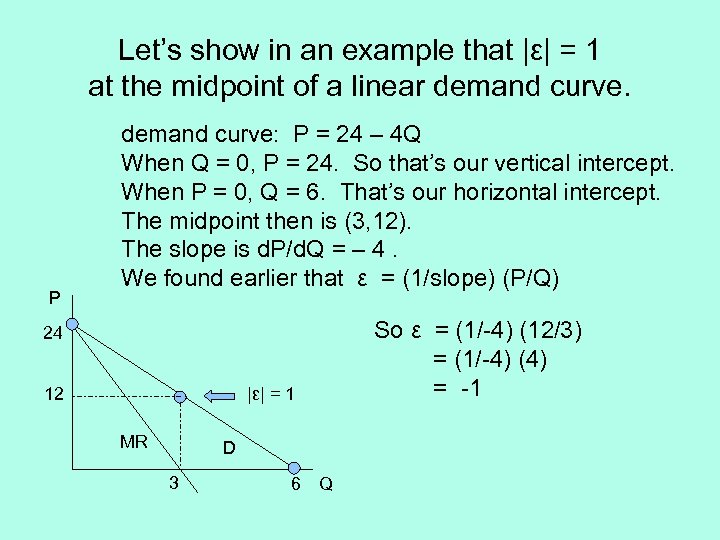 Let’s show in an example that |ε| = 1 at the midpoint of a linear demand curve. P demand curve: P = 24 – 4 Q When Q = 0, P = 24. So that’s our vertical intercept. When P = 0, Q = 6. That’s our horizontal intercept. The midpoint then is (3, 12). The slope is d. P/d. Q = – 4. We found earlier that ε = (1/slope) (P/Q) So ε = (1/-4) (12/3) = (1/-4) (4) = -1 24 12 |ε| = 1 MR D 3 6 Q
Let’s show in an example that |ε| = 1 at the midpoint of a linear demand curve. P demand curve: P = 24 – 4 Q When Q = 0, P = 24. So that’s our vertical intercept. When P = 0, Q = 6. That’s our horizontal intercept. The midpoint then is (3, 12). The slope is d. P/d. Q = – 4. We found earlier that ε = (1/slope) (P/Q) So ε = (1/-4) (12/3) = (1/-4) (4) = -1 24 12 |ε| = 1 MR D 3 6 Q
 Relationship between Elasticity & Total Revenue Price increase: |ε| > 1: P Q TR |ε| < 1: P Q TR |ε| = 1: P Q TR unchanged
Relationship between Elasticity & Total Revenue Price increase: |ε| > 1: P Q TR |ε| < 1: P Q TR |ε| = 1: P Q TR unchanged
 Relationship between Elasticity & Total Revenue Price decrease: |ε| > 1: P Q TR |ε| < 1: P Q TR |ε| = 1: P Q TR unchanged
Relationship between Elasticity & Total Revenue Price decrease: |ε| > 1: P Q TR |ε| < 1: P Q TR |ε| = 1: P Q TR unchanged
 The most profitable place to be is in the elastic portion of the demand curve. In the inelastic portion of the demand curve, marginal revenue is negative (additional units of output lower total revenue). While this is true in general, we can demonstrate it in the linear demand case.
The most profitable place to be is in the elastic portion of the demand curve. In the inelastic portion of the demand curve, marginal revenue is negative (additional units of output lower total revenue). While this is true in general, we can demonstrate it in the linear demand case.
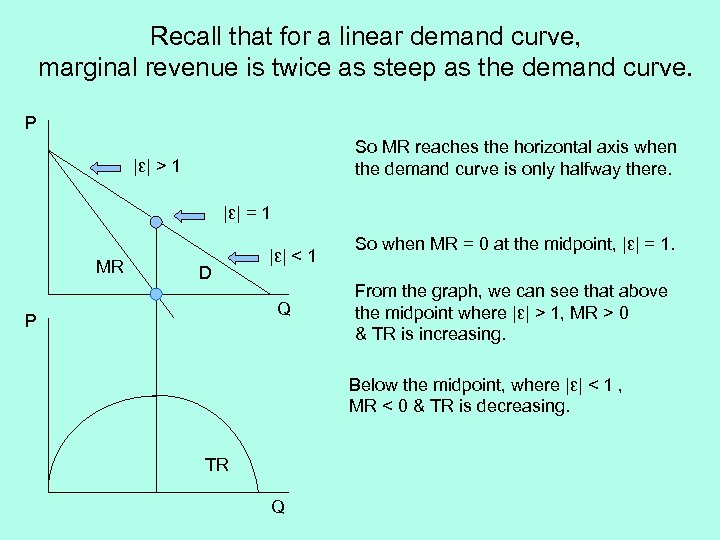 Recall that for a linear demand curve, marginal revenue is twice as steep as the demand curve. P So MR reaches the horizontal axis when the demand curve is only halfway there. |ε| > 1 |ε| = 1 MR D |ε| < 1 Q P So when MR = 0 at the midpoint, |ε| = 1. From the graph, we can see that above the midpoint where |ε| > 1, MR > 0 & TR is increasing. Below the midpoint, where |ε| < 1 , MR < 0 & TR is decreasing. TR Q
Recall that for a linear demand curve, marginal revenue is twice as steep as the demand curve. P So MR reaches the horizontal axis when the demand curve is only halfway there. |ε| > 1 |ε| = 1 MR D |ε| < 1 Q P So when MR = 0 at the midpoint, |ε| = 1. From the graph, we can see that above the midpoint where |ε| > 1, MR > 0 & TR is increasing. Below the midpoint, where |ε| < 1 , MR < 0 & TR is decreasing. TR Q
 Special Elasticity Cases
Special Elasticity Cases
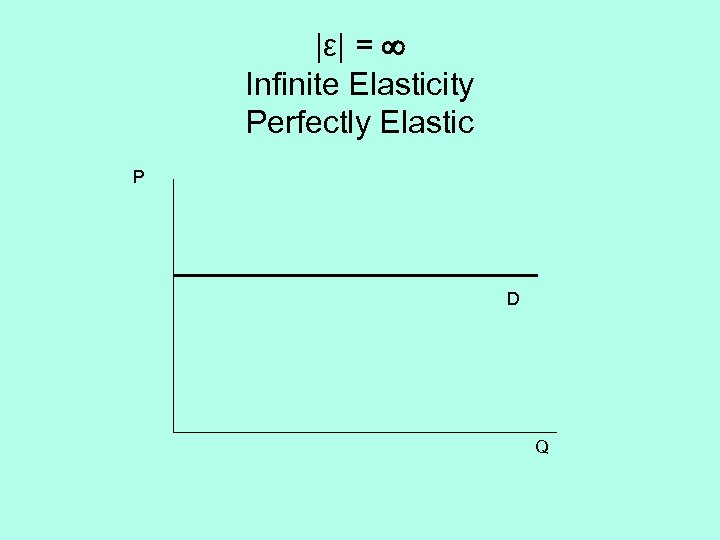 |ε| = Infinite Elasticity Perfectly Elastic P D Q
|ε| = Infinite Elasticity Perfectly Elastic P D Q
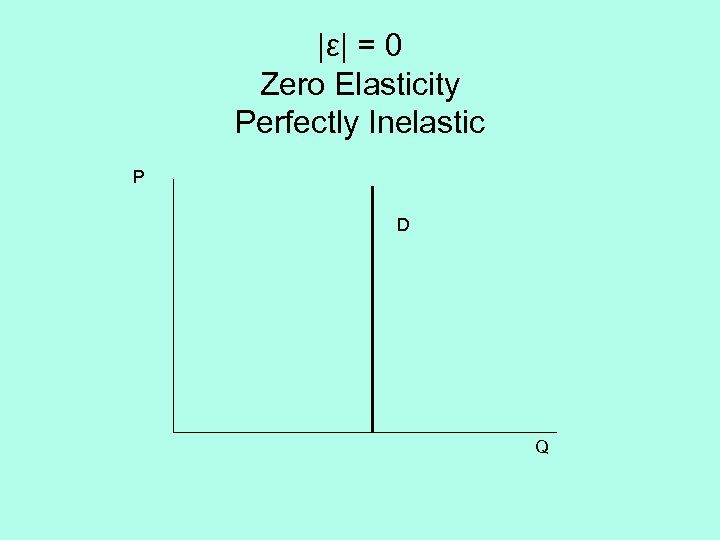 |ε| = 0 Zero Elasticity Perfectly Inelastic P D Q
|ε| = 0 Zero Elasticity Perfectly Inelastic P D Q
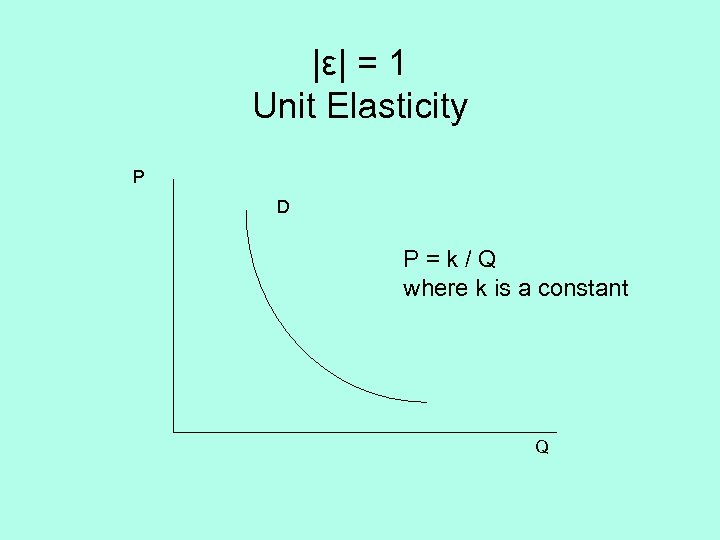 |ε| = 1 Unit Elasticity P D P=k/Q where k is a constant Q
|ε| = 1 Unit Elasticity P D P=k/Q where k is a constant Q
 Facts about Price Elasticity of Demand 1. The more substitutes there are for a product, the more elastic the demand. 2. An individual firm’s product has a more elastic demand than the entire industry’s product. 3. The longer the time period, the greater the elasticity of demand, because the greater the adjustments that are possible. 4. Products (like salt) that are a small part of the budget have low elasticities of demand.
Facts about Price Elasticity of Demand 1. The more substitutes there are for a product, the more elastic the demand. 2. An individual firm’s product has a more elastic demand than the entire industry’s product. 3. The longer the time period, the greater the elasticity of demand, because the greater the adjustments that are possible. 4. Products (like salt) that are a small part of the budget have low elasticities of demand.
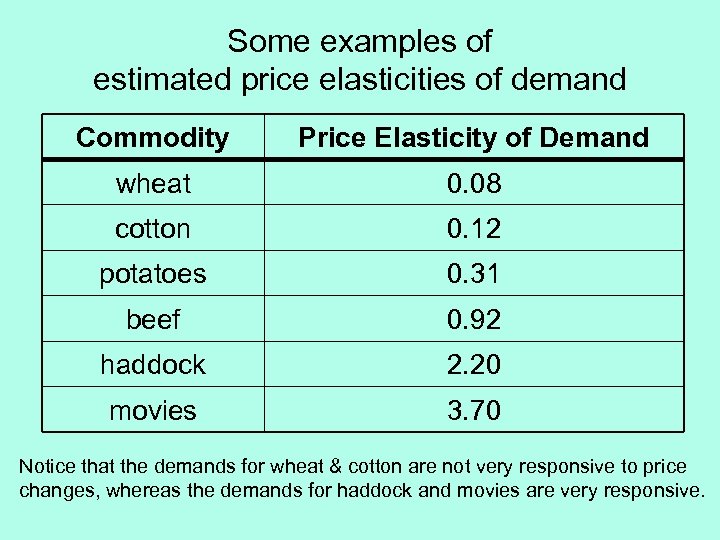 Some examples of estimated price elasticities of demand Commodity Price Elasticity of Demand wheat 0. 08 cotton 0. 12 potatoes 0. 31 beef 0. 92 haddock 2. 20 movies 3. 70 Notice that the demands for wheat & cotton are not very responsive to price changes, whereas the demands for haddock and movies are very responsive.
Some examples of estimated price elasticities of demand Commodity Price Elasticity of Demand wheat 0. 08 cotton 0. 12 potatoes 0. 31 beef 0. 92 haddock 2. 20 movies 3. 70 Notice that the demands for wheat & cotton are not very responsive to price changes, whereas the demands for haddock and movies are very responsive.
 So far the only elasticity that we have discussed is price elasticity of demand. There are other types of elasticities. Each type can be computed as arc elasticity or point elasticity.
So far the only elasticity that we have discussed is price elasticity of demand. There are other types of elasticities. Each type can be computed as arc elasticity or point elasticity.
 Income Elasticity of Demand εI (% change in quantity demanded) = ------------------------(% change in income)
Income Elasticity of Demand εI (% change in quantity demanded) = ------------------------(% change in income)
 Categories of Income Elasticity of Demand Normal Goods: εI > 1 income elastic εI = 1 unit income elastic 0 < εI < 1 income inelastic Luxury items have high income elasticities of demand, while necessities have low income elasticities of demand. Inferior Goods: εI < 0
Categories of Income Elasticity of Demand Normal Goods: εI > 1 income elastic εI = 1 unit income elastic 0 < εI < 1 income inelastic Luxury items have high income elasticities of demand, while necessities have low income elasticities of demand. Inferior Goods: εI < 0
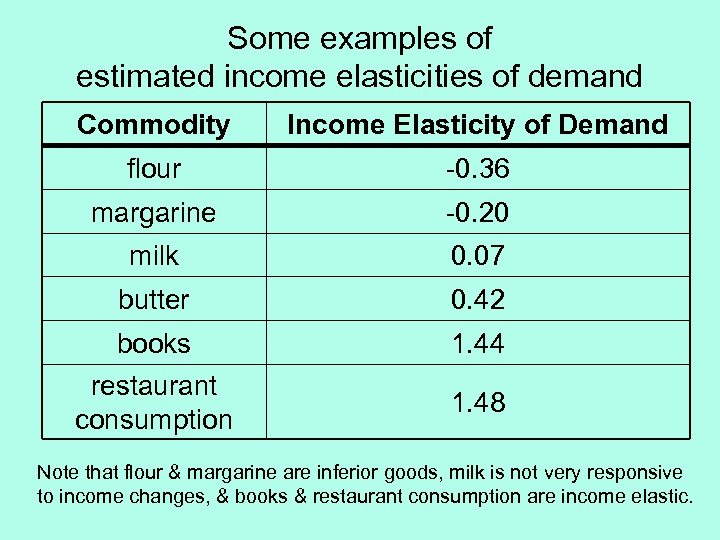 Some examples of estimated income elasticities of demand Commodity Income Elasticity of Demand flour -0. 36 margarine -0. 20 milk 0. 07 butter 0. 42 books 1. 44 restaurant consumption 1. 48 Note that flour & margarine are inferior goods, milk is not very responsive to income changes, & books & restaurant consumption are income elastic.
Some examples of estimated income elasticities of demand Commodity Income Elasticity of Demand flour -0. 36 margarine -0. 20 milk 0. 07 butter 0. 42 books 1. 44 restaurant consumption 1. 48 Note that flour & margarine are inferior goods, milk is not very responsive to income changes, & books & restaurant consumption are income elastic.
 Cross Elasticity of Demand εYX (% change in quantity demanded of Y) = -------------------------(% change in price of X)
Cross Elasticity of Demand εYX (% change in quantity demanded of Y) = -------------------------(% change in price of X)
 Categories of Cross Elasticity of Demand Substitutes: εYX > 0 The price of X & the quantity demanded of Y move in the same direction. When the price of X increases, you consume less of X and more of the goods that you can use in place of X. Complements: εYX < 0 The price of X & the quantity demanded of Y move in opposite directions. When the price of X increases, you consume less of X and less of the goods that you use with X.
Categories of Cross Elasticity of Demand Substitutes: εYX > 0 The price of X & the quantity demanded of Y move in the same direction. When the price of X increases, you consume less of X and more of the goods that you can use in place of X. Complements: εYX < 0 The price of X & the quantity demanded of Y move in opposite directions. When the price of X increases, you consume less of X and less of the goods that you use with X.
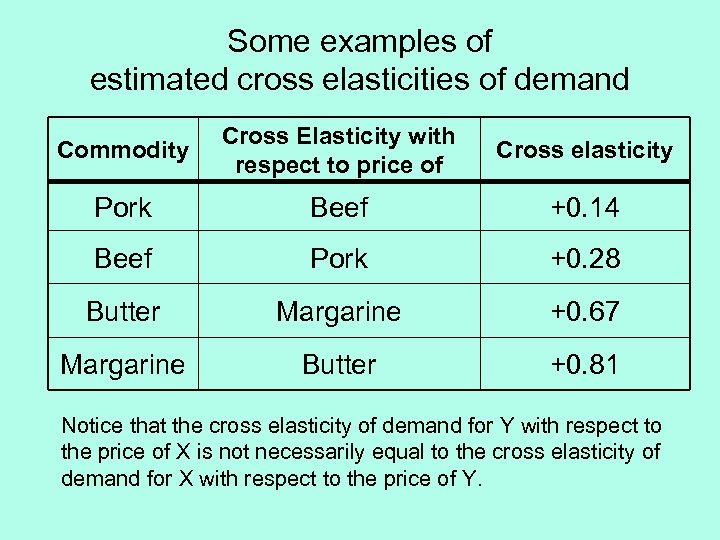 Some examples of estimated cross elasticities of demand Commodity Cross Elasticity with respect to price of Cross elasticity Pork Beef +0. 14 Beef Pork +0. 28 Butter Margarine +0. 67 Margarine Butter +0. 81 Notice that the cross elasticity of demand for Y with respect to the price of X is not necessarily equal to the cross elasticity of demand for X with respect to the price of Y.
Some examples of estimated cross elasticities of demand Commodity Cross Elasticity with respect to price of Cross elasticity Pork Beef +0. 14 Beef Pork +0. 28 Butter Margarine +0. 67 Margarine Butter +0. 81 Notice that the cross elasticity of demand for Y with respect to the price of X is not necessarily equal to the cross elasticity of demand for X with respect to the price of Y.
 Price Elasticity of Supply εS (% change in quantity supplied) = ------------------------(% change in price)
Price Elasticity of Supply εS (% change in quantity supplied) = ------------------------(% change in price)
 Categories of Price Elasticity of Supply is elastic if Supply is inelastic if Supply is unit elastic if εS > 1 εS < 1 εS = 1
Categories of Price Elasticity of Supply is elastic if Supply is inelastic if Supply is unit elastic if εS > 1 εS < 1 εS = 1


