Demand Utility and Expenditure Chapter 5 Frank and

Demand, Utility and Expenditure Chapter 5, Frank and Bernanke

Key Concepts Law of Demand – other things equal, when price goes up, the quantity demanded goes down. Utility maximization – consumers determine the quantity demanded of each of two goods by equating their marginal utility per dollar. Demand expenditure – the Law of Demand makes no prediction on the relation of price and expenditure. When price goes up, expenditure may go up, go down or stay the same. Expenditure = price times quantity purchased. Elasticity = responsiveness of quantity demanded to price changes.

Utility Maximization • Consumers apply the equimarginal principle and find the point at which the marginal benefit of spending another dollar on Good X equals the marginal cost of NOT spending another dollar on Good Y. MUx MUy Px Py • This equation is the “rational spending rule”

Application of the Rational Spending Rule • Suppose good X (“pizza”) is at a price of $10 a pie, and good Y (“concert tickets”) is at a price of $30 a concert. • You have a budget of $ 130 for entertainment, and want to rationally allocate it among the two goods. • You know that the marginal utility of either good declines with the amount consumed (though TOTAL utility continues to increase) • You know your utility tables – see the next slide

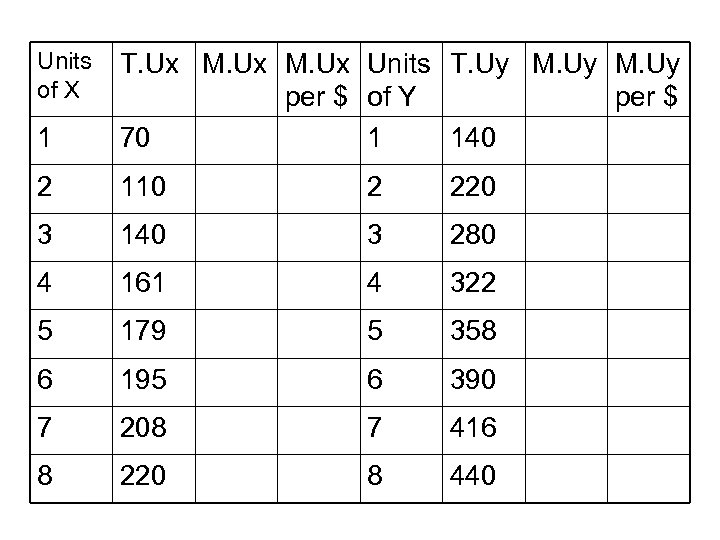Units of X 1 T. Ux M. Ux Units T. Uy M. Uy per $ of Y per $ 70 1 140 2 110 2 220 3 140 3 280 4 161 4 322 5 179 5 358 6 195 6 390 7 208 7 416 8 220 8 440

• Finding marginal utility: – MU of X = change in total utility from X with 1 more X – MU of Y = change in total utility from Y with 1 more Y • Finding marginal utility per dollar: – MU per dollar of X is the MU of X divided by the price of X – And likewise for the MU per dollar of Y. • The last is the crucial step – we are changing our choices dollar by dollar, not unit by unit.

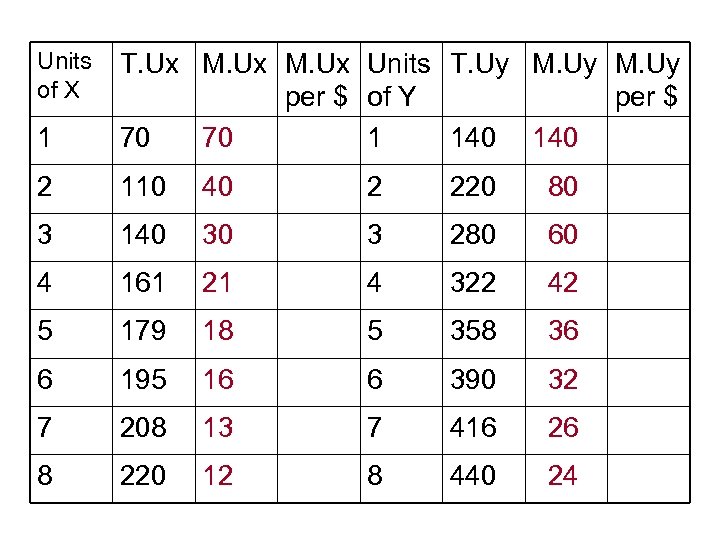Units of X 1 T. Ux M. Ux Units T. Uy M. Uy per $ of Y per $ 70 70 1 140 2 110 40 2 220 80 3 140 30 3 280 60 4 161 21 4 322 42 5 179 18 5 358 36 6 195 16 6 390 32 7 208 13 7 416 26 8 220 12 8 440 24

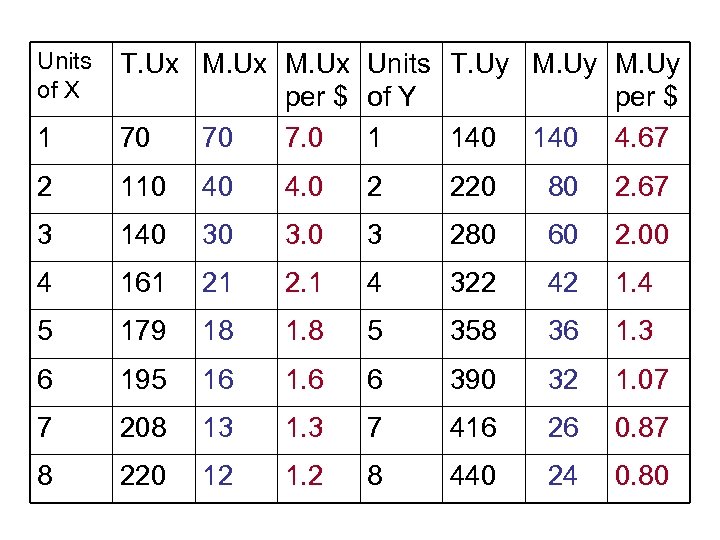Units of X 1 T. Ux M. Ux Units T. Uy M. Uy per $ of Y per $ 70 70 7. 0 1 140 4. 67 2 110 40 4. 0 2 220 80 2. 67 3 140 30 3. 0 3 280 60 2. 00 4 161 21 2. 1 4 322 42 1. 4 5 179 18 1. 8 5 358 36 1. 3 6 195 16 1. 6 6 390 32 1. 07 7 208 13 1. 3 7 416 26 0. 87 8 220 12 1. 2 8 440 24 0. 80

• • Using the table The problem can’t be easily solved by considering all possible choices. Reduce it to the simpler problem: what do I buy next? Since for the first unit MU of x per $ is 7. 0, and MU of y per $ is 4. 67, buy X first. Now compare the MU per dollar of the second unit of X ( 4. 0) with the MU per dollar of the first unit of Y (4. 67). Buy Y next.

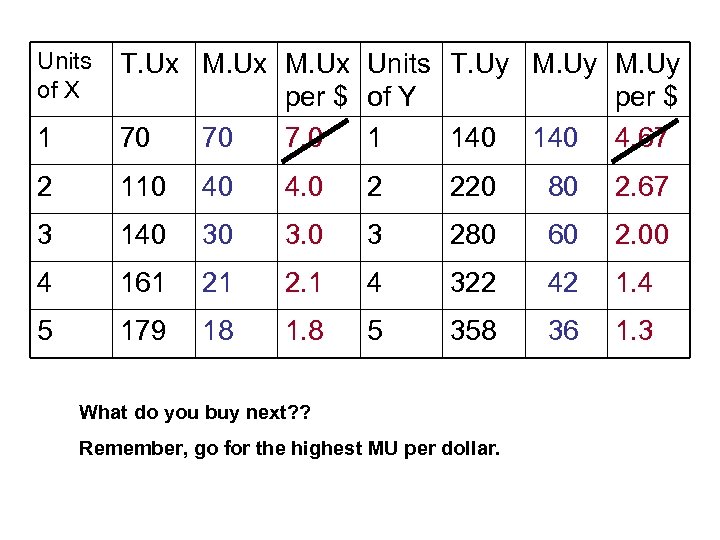Units of X 1 T. Ux M. Ux Units T. Uy M. Uy per $ of Y per $ 70 70 7. 0 1 140 4. 67 2 110 40 4. 0 2 220 80 2. 67 3 140 30 3. 0 3 280 60 2. 00 4 161 21 2. 1 4 322 42 1. 4 5 179 18 1. 8 5 358 36 1. 3 What do you buy next? ? Remember, go for the highest MU per dollar.

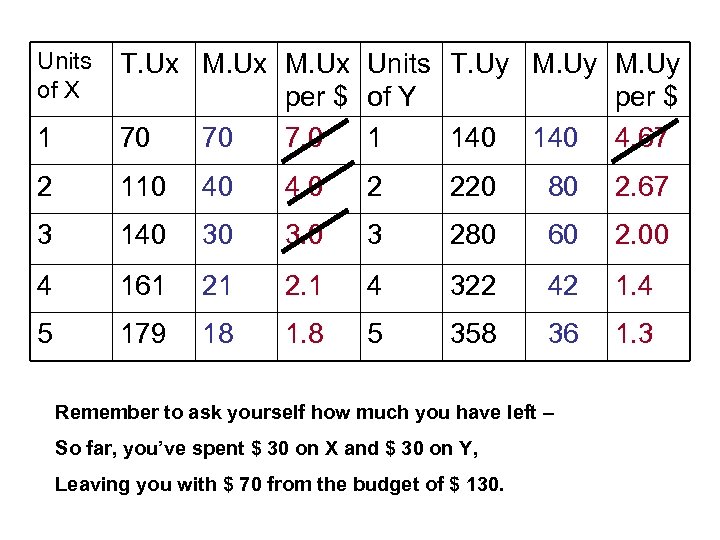Units of X 1 T. Ux M. Ux Units T. Uy M. Uy per $ of Y per $ 70 70 7. 0 1 140 4. 67 2 110 40 4. 0 2 220 80 2. 67 3 140 30 3. 0 3 280 60 2. 00 4 161 21 2. 1 4 322 42 1. 4 5 179 18 1. 8 5 358 36 1. 3 Remember to ask yourself how much you have left – So far, you’ve spent $ 30 on X and $ 30 on Y, Leaving you with $ 70 from the budget of $ 130.

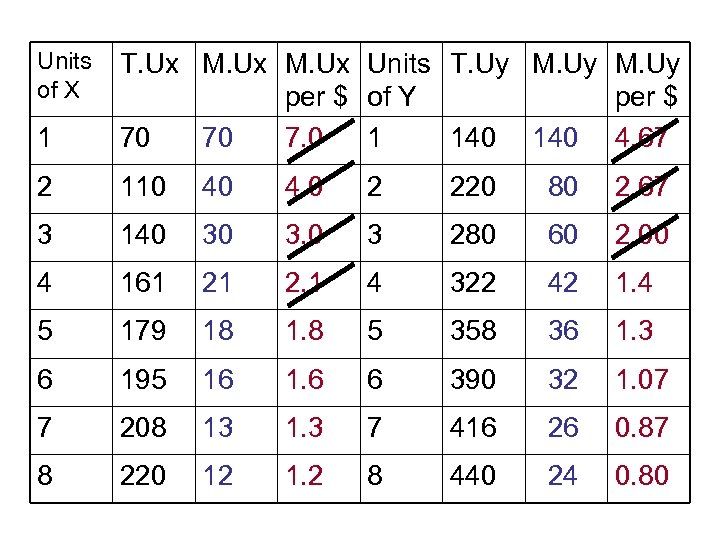Units of X 1 T. Ux M. Ux Units T. Uy M. Uy per $ of Y per $ 70 70 7. 0 1 140 4. 67 2 110 40 4. 0 2 220 80 2. 67 3 140 30 3. 0 3 280 60 2. 00 4 161 21 2. 1 4 322 42 1. 4 5 179 18 1. 8 5 358 36 1. 3 6 195 16 1. 6 6 390 32 1. 07 7 208 13 1. 3 7 416 26 0. 87 8 220 12 1. 2 8 440 24 0. 80

Checking the rational spending rule At X = 4 and Y = 3, we’ve exhausted our budget ($ 40 on X, $ 90 on Y) Go back to the table to calculate our utility score: Utility of 4 X = 161 utils Utility of 3 Y = 280 utils Total utility = 441 utils

• Could we do better? If we bought one less Y, we would have $ 30 more and could buy 3 more X : • The new consumption bundle is 2 Y and 7 X – Utility of 7 X = 208 utils – Utility of 2 Y = 220 utils – Total utility = 428 utils (less than 441 utils) • Try buying one more Y and 3 less X: – Utility of 1 X = 70 utils – Utility of 4 Y = 322 utils – Total utility = 392 utils

Utility maximization, functionally speaking • A common economic model for a utility function is the logarithmic function: • TUx = 100 ln X • TUy = 200 ln Y (it wasn’t an accident that the tables just used are almost the same as you would get from computing 100 ln 2, 100 ln 3, etc. The only slight difference is that ln 1 = 0, so the table was shifted back 1 level to avoid TU of 1 = 0).

Marginal Utility, functionally speaking • It can be shown that if TUx = A ln X, MUx = A divided by X Full proof requires calculus, but you should be able to see that the formula works by a few examples: If TUx = 100 ln X, what is the marginal utility between 50 and 51 units of X? MUx = 100 ln 51 minus 100 ln 50 MUx = 393. 1826 minus 391. 2023 = 1. 9803 Using the formula for marginal utility, MUx = 100 / X = 100 / 50. 5 = 1. 9802 [should you divide by 50 or 51? Dividing by 50 gets MUx = 2, by 51 gets MUx = 1. 96 The difference is never too important in practice]

Rational spending, functionally speaking • Let TUx = 150 ln X and TUy = 300 ln Y • Then MUx = 100 / X and MUy = 300 / Y • Hence the rational spending rule is: MUx / Px = MUy / Py or 150 / Px X = 300 Py Y or Py Y = 2 Px X