Demand Theory and Analysis LECTURE 3 ECON 340

Demand Theory and Analysis LECTURE 3 ECON 340 MANAGERIAL ECONOMICS Christopher Michael Trent University Department of Economics © 2006 by Nelson, a division of Thomson Canada Limited 3/17/2018 1

Topics • • • Demand Relationships Demand Elasticities Income Elasticities Cross Elasticities of Demand Combined Effects of Elasticities Indifference Curve Analysis © 2006 by Nelson, a division of Thomson Canada Limited 2

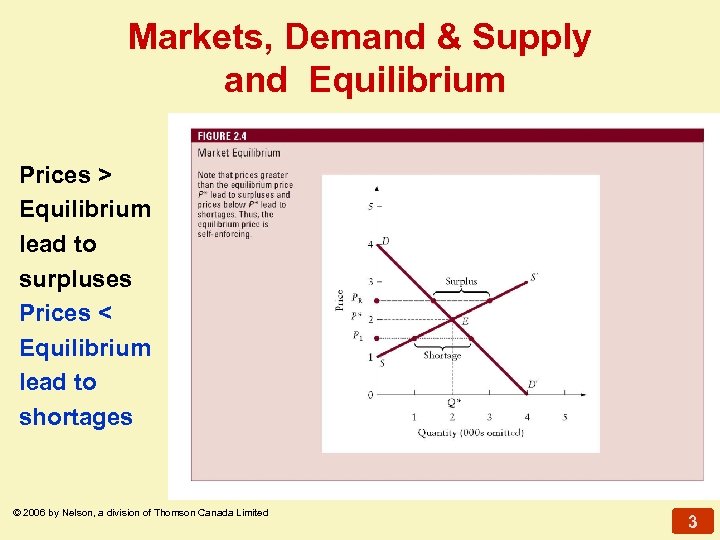Markets, Demand & Supply and Equilibrium Prices > Equilibrium lead to surpluses Prices < Equilibrium lead to shortages © 2006 by Nelson, a division of Thomson Canada Limited 3

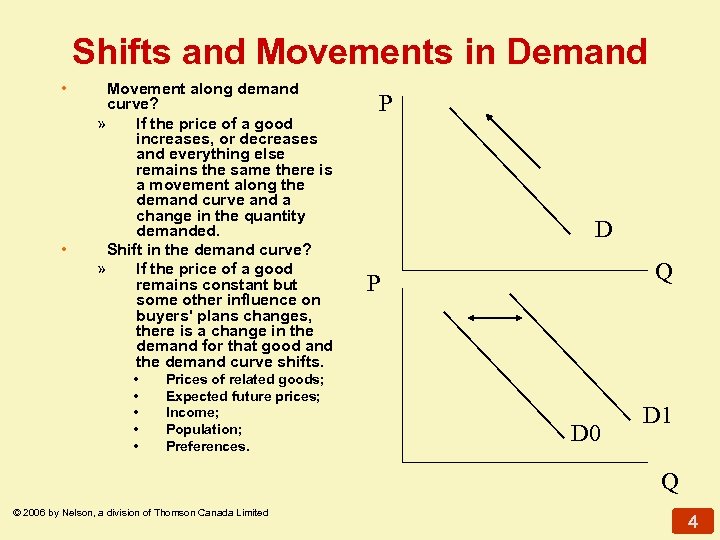Shifts and Movements in Demand • • Movement along demand curve? » If the price of a good increases, or decreases and everything else remains the same there is a movement along the demand curve and a change in the quantity demanded. Shift in the demand curve? » If the price of a good remains constant but some other influence on buyers' plans changes, there is a change in the demand for that good and the demand curve shifts. • • • Prices of related goods; Expected future prices; Income; Population; Preferences. P D Q P D 0 D 1 Q © 2006 by Nelson, a division of Thomson Canada Limited 4

Health Care & Cigarettes • Raising cigarette taxes reduces smoking » In Canada, $4 for a pack of cigarettes reduced smoking 38% in a decade • But cigarette taxes also helps fund health care initiatives » The issue then, should we find a tax rate that maximizes tax revenues? » Or a tax rate that reduces smoking? © 2006 by Nelson, a division of Thomson Canada Limited 5

Demand Analysis • An important contributor to firm risk arises from sudden shifts in demand for the product or service. • Demand analysis serves two managerial objectives: (1) it provides the insights necessary for effective management of demand, and (2) it aids in forecasting sales and revenues. © 2006 by Nelson, a division of Thomson Canada Limited 6

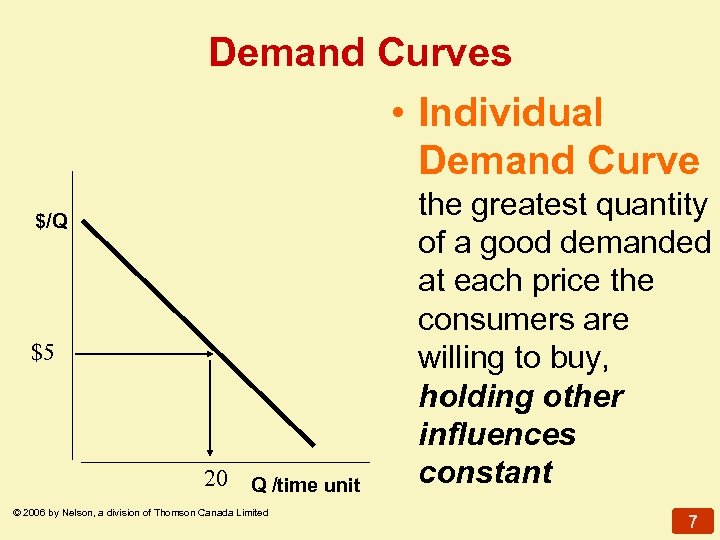Demand Curves • Individual Demand Curve $/Q $5 20 Q /time unit © 2006 by Nelson, a division of Thomson Canada Limited the greatest quantity of a good demanded at each price the consumers are willing to buy, holding other influences constant 7

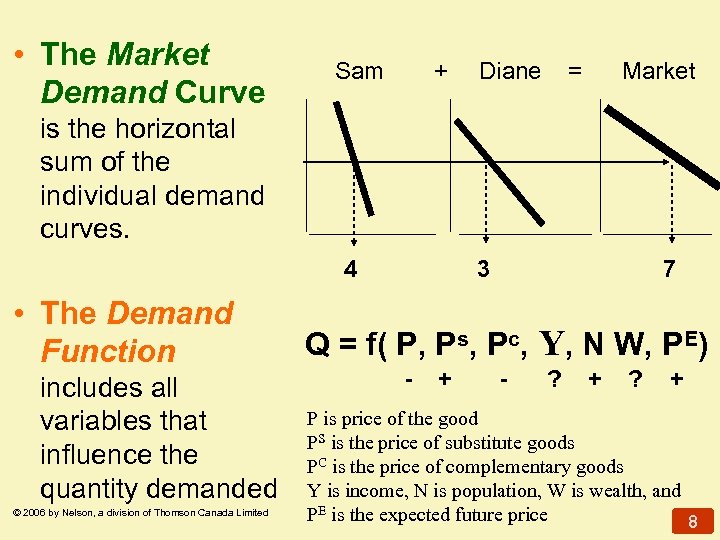• The Market Demand Curve Sam + Diane = Market is the horizontal sum of the individual demand curves. 4 • The Demand Function includes all variables that influence the quantity demanded © 2006 by Nelson, a division of Thomson Canada Limited 3 7 Q = f( P, Ps, Pc, Y, N W, PE) - + - ? + P is price of the good PS is the price of substitute goods PC is the price of complementary goods Y is income, N is population, W is wealth, and PE is the expected future price 8

Why is the Demand Curve Downward Sloping? ? • Reasons that price and quantity are negatively related include: » income effect — as the price of a good declines, the consumer can purchase more of all goods since one’s real income increased. » substitution effect — as the price declines, the good becomes relatively cheaper. A rational consumer maximizes satisfaction by reorganizing consumption until the marginal utility in each good per dollar is equal. © 2006 by Nelson, a division of Thomson Canada Limited 9

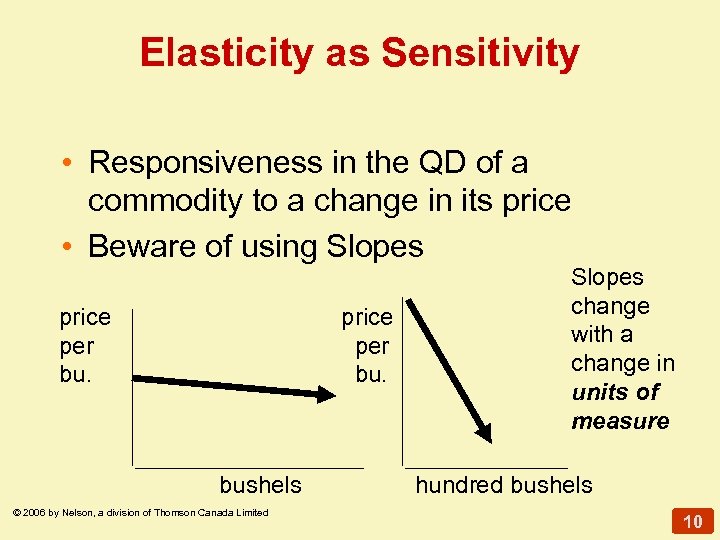Elasticity as Sensitivity • Responsiveness in the QD of a commodity to a change in its price • Beware of using Slopes price per bu. bushels © 2006 by Nelson, a division of Thomson Canada Limited Slopes change with a change in units of measure hundred bushels 10

Price Elasticity • • • ED = % change in Q / % change in P Shortcut notation: ED = % Q / % P A percentage change from 100 to 150 is 50% A percentage change from 150 to 100 is -33% For arc elasticities, we use the average as the base, as in 100 to 150 is +50/125 = 40%, and 150 to 100 is -40% • Arc Price Elasticity -- averages over the two points Average quantity ED = Q/ [(Q 1 + Q 2)/2] P/ [(P 1 + P 2)/2] arc price elasticity D Average price © 2006 by Nelson, a division of Thomson Canada Limited 11

Arc Price Elasticity Example • • Q = 1000 when the price is $10 Q= 1200 when the price is reduced to $6 Find the arc price elasticity Solution: ED = % Q/ % P = +200/1100 -4/8 or -0. 3636. The answer is a number. A 1% increase in price reduces quantity by 0. 36 percent. © 2006 by Nelson, a division of Thomson Canada Limited 12

Price Point Elasticity Example • Need a demand curve or demand function to find the price elasticity at a point. ED = % Q/ % P =( Q/ P)(P/Q) If Q = 500 - 5 • P, find the point price elasticity at P = 30; P = 50; and P = 80 1. ED = ( Q/ P)(P/Q) = - 5(30/350) = - 0. 43 2. ED = ( Q/ P)(P/Q) = - 5(50/250) = - 1. 00 3. ED = ( Q/ P)(P/Q) = - 5(80/100) = - 4. 00 © 2006 by Nelson, a division of Thomson Canada Limited 13

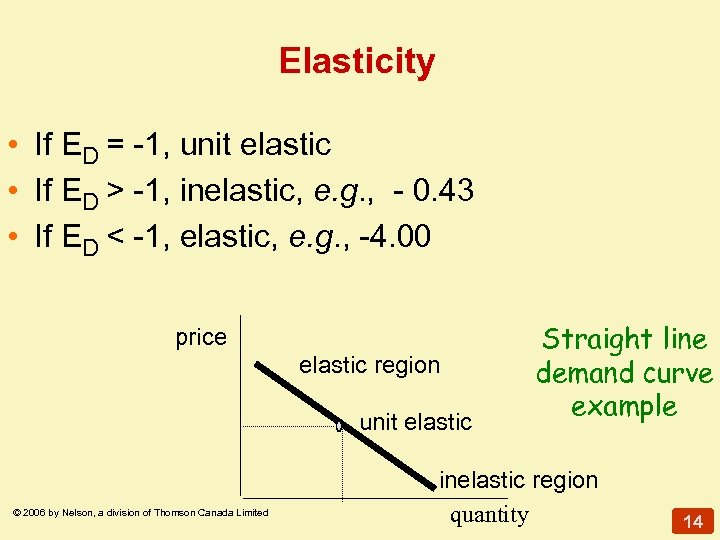Elasticity • If ED = -1, unit elastic • If ED > -1, inelastic, e. g. , - 0. 43 • If ED < -1, elastic, e. g. , -4. 00 price elastic region unit elastic © 2006 by Nelson, a division of Thomson Canada Limited Straight line demand curve example inelastic region quantity 14

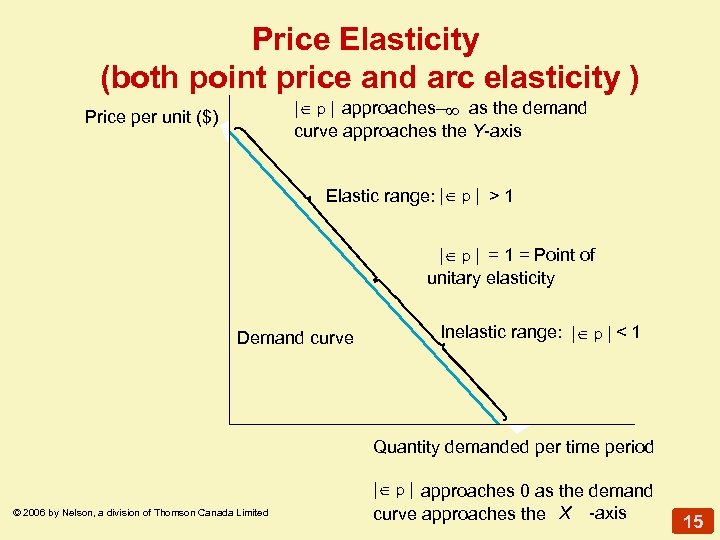Price Elasticity (both point price and arc elasticity ) | p | approaches– as the demand curve approaches the Y-axis Price per unit ($) Elastic range: | p | > 1 | p | = 1 = Point of unitary elasticity Demand curve Inelastic range: | p | < 1 Quantity demanded per time period © 2006 by Nelson, a division of Thomson Canada Limited | p | approaches 0 as the demand curve approaches the X -axis 15

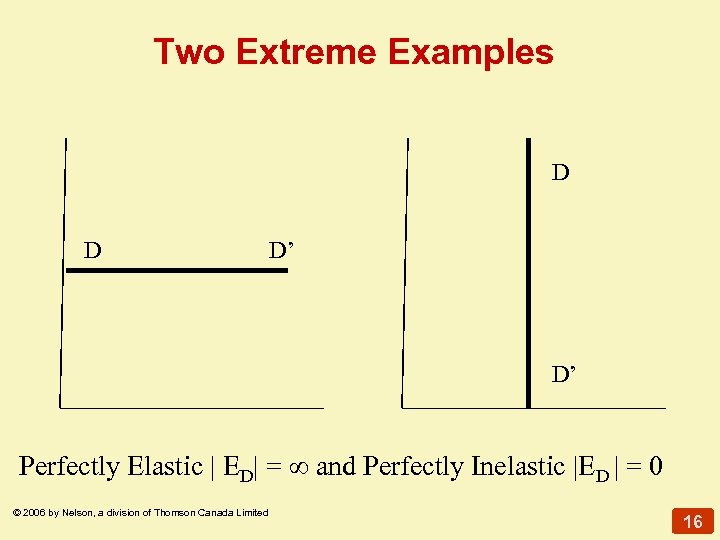Two Extreme Examples D D D’ D’ Perfectly Elastic | ED| = ∞ and Perfectly Inelastic |ED | = 0 © 2006 by Nelson, a division of Thomson Canada Limited 16

TR and Price Elasticities • If you raise price, does TR rise? • Suppose demand is elastic, and raise price. TR = P • Q, so, % TR = % P + % Q • If elastic, P , but Q a lot • Hence TR FALLS !!! • Suppose demand is inelastic, and we decide to raise price. What happens to TR and TC and profit? © 2006 by Nelson, a division of Thomson Canada Limited 17

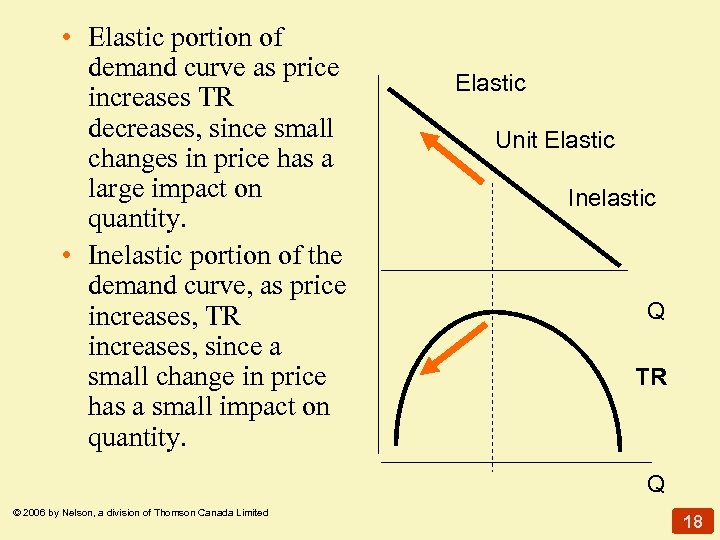• Elastic portion of demand curve as price increases TR decreases, since small changes in price has a large impact on quantity. • Inelastic portion of the demand curve, as price increases, TR increases, since a small change in price has a small impact on quantity. Elastic Unit Elastic Inelastic Q TR Q © 2006 by Nelson, a division of Thomson Canada Limited 18

MR and Elasticity • Marginal revenue is TR / Q • To sell more, often price must decline, so MR is often less than the price. à MR = P ( 1 + 1/ED ) • For a perfectly elastic demand, ED = -∞. Hence, MR = P. • If ED = -2, then MR = 0. 5 • P, or is half of the price. © 2006 by Nelson, a division of Thomson Canada Limited 19

Determinants of the Price Elasticity • The availability and the closeness of substitutes » more substitutes, more elastic • The more durable is the product » Durable goods are more elastic than non-durables • The percentage of the budget » larger proportion of the budget, more elastic • The longer the time period permitted » more time, generally, more elastic » consider examples of business travel versus vacation travel for all three above. © 2006 by Nelson, a division of Thomson Canada Limited 20

Income Elasticity EY = % Q/ % Y = ( Q/ Y)( Y/Q) point income EY = Q/ [(Q 1 + Q 2)/2] arc income Y/ [(Y 1 + Y 2)/2] elasticity • arc income elasticity: » suppose dollar quantity of food expenditures of families of $20, 000 is $5, 200; and food expenditures rises to $6, 760 for families earning $30, 000. » Find the income elasticity of food » % Q/ % Y = (1560/5980)÷(10, 000/25, 000) =0. 652 » With a 1% increase in income, food purchases rise 0. 652% © 2006 by Nelson, a division of Thomson Canada Limited 21

Income Elasticity Definitions • If EY >0, then it is a normal good » some goods are Luxuries: EY > 1 with a high income elasticity (luxuries are also called superior goods) » some goods are Necessities: EY < 1 with a low income elasticity • • If EY is negative, then it’s an inferior good Consider these examples: 1. Expenditures on new automobiles 2. Expenditures on new Chevrolets 3. Expenditures on 1996 Chevy Cavaliers with 150, 000 km Which of the above is likely to have the largest income elasticity? Which of the above might have a negative income elasticity? © 2006 by Nelson, a division of Thomson Canada Limited 22

Point Income Elasticity Problem • Suppose the demand function is: Q = 10 - 2 • P + 3 • Y • find the income and price elasticities at a price of P = 2, and income Y = 10 • So: Q = 10 -2(2) + 3(10) = 36 • EY = ( Q/ Y)( Y/Q) = 3(10/ 36) = 0. 833 • ED = ( Q/ P)(P/Q) = -2(2/ 36) = -0. 111 • Characterize this demand curve, which means describe them using elasticity terms. © 2006 by Nelson, a division of Thomson Canada Limited 23

Cross Price Elasticities EX = % QA / % PB = ( QA/ PB)(PB /QA) • Substitutes have positive cross price elasticities: butter & margarine • Complements have negative cross price elasticities: DVD machines and the rental price of DVDs at Blockbuster • When the cross price elasticity is zero or insignificant, the products are not related © 2006 by Nelson, a division of Thomson Canada Limited 24

Problem • Find the point price elasticity, the point income elasticity, and the point cross-price elasticity at P=10, Y=20, and Ps=9, if the demand function were estimated to be: QD = 90 - 8·P + 2·Y + 2·Ps • Is the demand for this product elastic or inelastic? Is it a luxury or a necessity? Does this product have a close substitute or complement? • Find the point elasticities of demand. © 2006 by Nelson, a division of Thomson Canada Limited 25

Answer • First find the quantity at these prices and income: QD = 90 - 8·P + 2·Y + 2·Ps = 90 8· 10 + 2· 20 + 2· 9 =90 -80 +40 +18 = 68 • ED = ( Q/ P)(P/Q) = (-8)(10/68)= -1. 18 which is elastic • EY = ( Q/ Y)(Y/Q) = (2)(20/68) = +0. 59 which is a normal good, but a necessity • EX = ( QA/ PB)(PB /QA) = (2)(9/68) = +0. 26 which is a mild substitute © 2006 by Nelson, a division of Thomson Canada Limited 26

Combined Effect of Demand Elasticities • Most managers find that prices and income change every year. The combined effect of several changes are additive. % Q = ED(% P) + EY(% Y) + EX(% PR) » where P is price, Y is income, and PR is the price of a related good. • If you knew the price, income, and cross price elasticities, then you can forecast the percentage changes in quantity. © 2006 by Nelson, a division of Thomson Canada Limited 27

Example: Combined Effects of Elasticities • Toro has a price elasticity of -2 for snow blowers • Toro snow blowers have an income elasticity of 1. 5 • The cross price elasticity with professional snow removal for residential properties is +0. 50 • What will happen to the quantity sold if you raise price 3%, income rises 2%, and professional snow removal companies raise price 1%? » % Q = EP • % P +EY • % Y + EX • % Px = -2 • 3% + 1. 5 • 2% +0. 50 • 1% = -6% + 3% + 0. 5% » % Q = -2. 5%. We expect sales to decline. © 2006 by Nelson, a division of Thomson Canada Limited 28

Example (concluded): Combined Effects of Elasticities Q: Will Total Revenue for your product rise or fall? A: Total revenue will rise slightly (about + 0. 5%), as the price went up 3% and the quantity of snow blowers sold will fall 2. 5%. © 2006 by Nelson, a division of Thomson Canada Limited 29

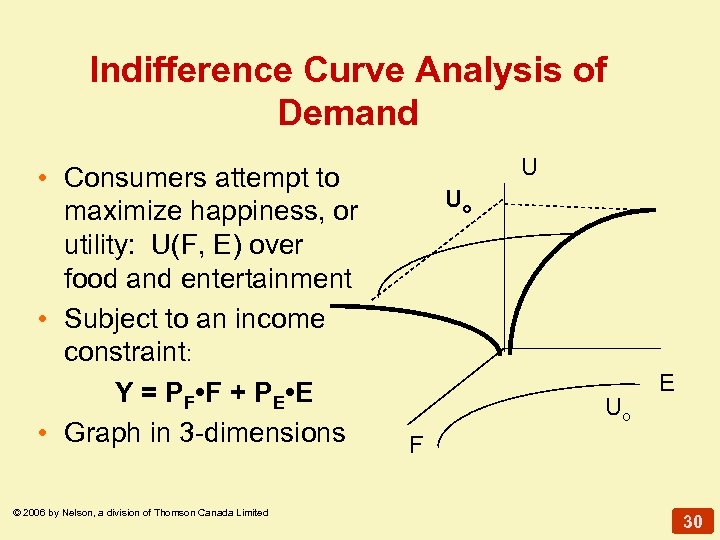Indifference Curve Analysis of Demand • Consumers attempt to maximize happiness, or utility: U(F, E) over food and entertainment • Subject to an income constraint: Y = PF • F + PE • Graph in 3 -dimensions © 2006 by Nelson, a division of Thomson Canada Limited U Uo Uo E F 30

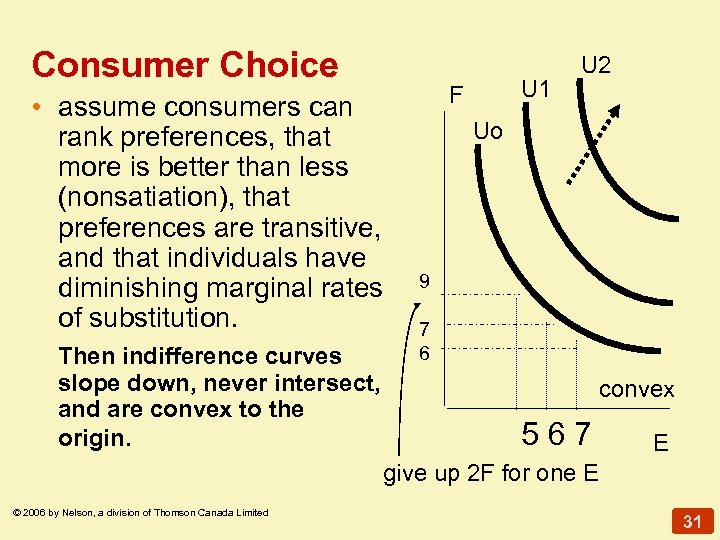Consumer Choice • assume consumers can rank preferences, that more is better than less (nonsatiation), that preferences are transitive, and that individuals have diminishing marginal rates of substitution. Then indifference curves slope down, never intersect, and are convex to the origin. U 1 F U 2 Uo 9 7 6 convex 567 E give up 2 F for one E © 2006 by Nelson, a division of Thomson Canada Limited 31

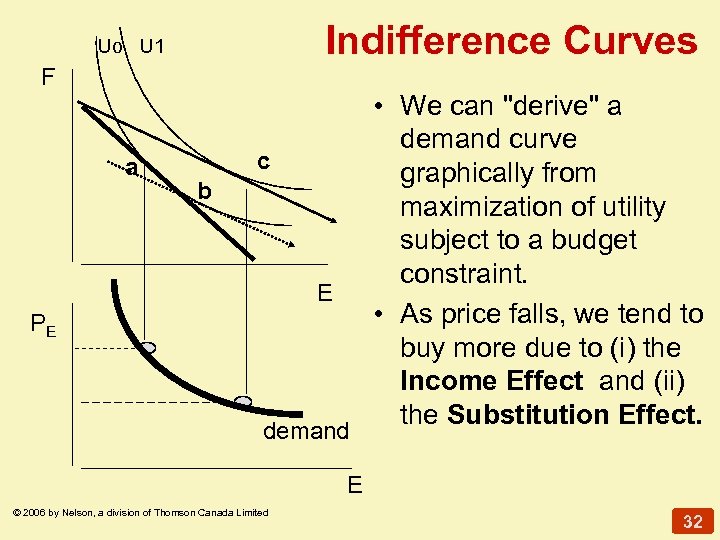Indifference Curves Uo U 1 F a c b E PE demand • We can "derive" a demand curve graphically from maximization of utility subject to a budget constraint. • As price falls, we tend to buy more due to (i) the Income Effect and (ii) the Substitution Effect. E © 2006 by Nelson, a division of Thomson Canada Limited 32

Optimal Consumption Point • Optimality Condition: MUF / PF = MUE / PE “ the marginal utility per dollar in each use is equal” MU 1 = 20, and MU 2 = 50 and P 1 = 5, and P 2 = 25 are you maximizing utility? Suppose © 2006 by Nelson, a division of Thomson Canada Limited 33