Demand Elasticities and Related Coefficients Demand Curve

Demand Elasticities and Related Coefficients

Demand Curve n Demand curves are assumed to be downward sloping, but the responsiveness of quantity (Q) to changes in price (P) is not the same for all commodities n Units of commodities are also different (bushels, lbs. kg. , etc. )

Elasticities n Elasticities are used to estimate responsiveness of Q to changes in P and are in percentages so one can make comparisons across commodities

Own-Price Elasticity n The most commonly used elasticity is the “own- price” elasticity. This means the responsiveness of the quantity demanded of a commodity to a change in its own price. Point elasticity for own-price or At a given point on a demand curve.

Arc Elasticity n Over larger segments of the demand curve (i. e. , for relatively large changes in price), the arc elasticity may be more appropriate because it give an average elasticity over the affected portion of the demand curve. = Arc elasticity

Degree of Responsiveness n The own price elasticity is said to be: n Elastic if the absolute value of the elasticity is greater than 1 n Inelastic if the absolute value of the elasticity is less than 1 n Unitary elastic if the absolute value of the elasticity is equal to 1

What Does the Degree of Responsiveness Tell Us n Essentially the degree of responsiveness indicates what will happen to total revenue (i. e. , sales) when price changes n Total revenue (TR) = P*Q n Because demand curves are downward sloping P and Q vary inversely. That is, if P increases (decreases) then Q decreases (increases). Consequently, the effect of a change in price on TR is uncertain and depends on the elasticity of demand.

Example of Effect of Elasticity on Total Revenue n If P=100 and Q=100, then TR =10, 000 (100 * 100) n If ED = -0. 5 and P increases by 1% to 101, then Q decreases by one-half of 1% to 99. 5. The effect is that TR actually increases to 10, 049 (101*99. 5). n If instead ED=-1. 5 and P increases by 1% to 101, then Q decreases by one and one-half % to 98. 8. The effect is than TR decreases to 9, 948. 5 (101*98. 5). n So, with inelastic demand TR increases (decrease) as P increases (decreases). With elastic demand TR decreases (increases) as P increases (decreases). n The demand for most agricultural commodities is inelastic which means TR to that commodity goes up when P increases.

Income Elasticity n The income elasticity measures the sensitivity of quantity demanded to changes in income, other factors held constant:

Lessons from Income Elasticities n Income elasticities for food are generally thought to decline as income increases. Total amount of food consumed may not change much as income increases, but expenditures on food may increase as income increases. Market growth for bulk commodities is likely most easily achieved in developing economies n Market growth in developed economies is likely for highly processed, or other valueadding activities for food n

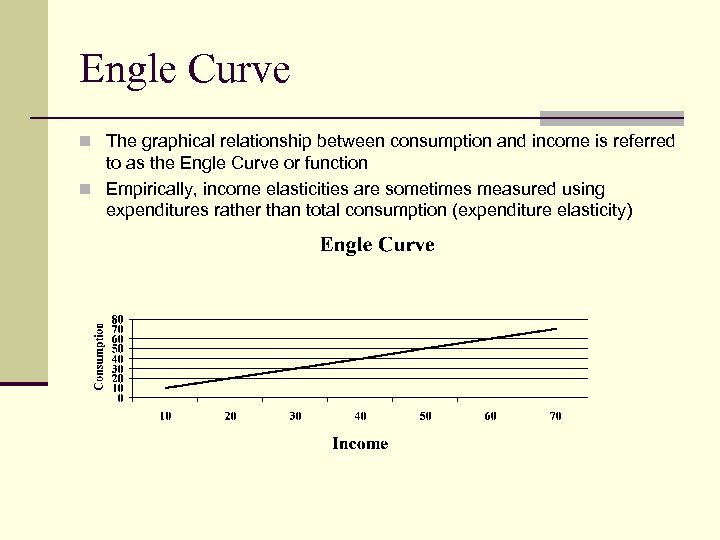Engle Curve n The graphical relationship between consumption and income is referred to as the Engle Curve or function n Empirically, income elasticities are sometimes measured using expenditures rather than total consumption (expenditure elasticity)

Properties of Income and Expenditure Elasticities n Expenditure elasticities tend to be larger than income elasticities. n The expenditure elasticity capture quality and quantity effects since as income changes people tend to buy more and also buy higher quality n Normal good = Ey > 0 n Inferior good = Ey < 0

Cross-Price Elasticities n Cross-price elasticities measure the responsiveness of demand for one good in relation to a change in price for another good.

Characteristics of Cross-Price Elasticities n If Eij > 0 then the two goods are substitutes Eij < 0 then the two goods are compliments If Eij = 0 then good i is independent from good j. n If n n The larger the cross-price elasticity (in terms of absolute value) the closer the relationship between the two goods.

Relationships Among Elasticities n Demand theory dictates that an exhaustive set of elasticities (price, income, and cross) have certain qualities. These qualities are: Homogeneity condition n Symmetry condition n Engle aggregation condition n n These conditions are used to calculate a number of elasticities from just a few. These conditions are also referred to as “restrictions” on elasticities.

Homogeneity Condition n States that for any good the sum of its own price elasticity, all of the cross price elasticities associated with the good, and its income elasticity =0 Implications of this are: 1. Cross-price elasticities are large (close substitutes exist) then 2. the good’s own price elasticity must also be large (in terms of 3. absolute value) or, in other words, less elastic. 2. If the cross-price elasticities are small then both the own-price elasticity 3. will tend to be more inelastic and will more closely resemble the 4. income elasticity in absolute value.

Symmetry Condition n The symmetry condition indicates what the relationship between cross-price elasticities must be. Where the “R” represent the proportion of income spent on that good. This implies that cross-price elasticities are symmetric, i. e. , , when the proportion of income spent on both goods is equal and their income elasticities are also equal.

Example Using Symmetry Condition n Lamb = 0. 1% of expenditures n Beef = 2% of expenditures n If a 1% increase in the price of beef increases demand for lamb by 0. 6% (i. e. , cross price elasticity of beef on lamb of 0. 6 (i. e. , ) Or, assuming that the income elasticities are equal then a 1% change in the price of lamb will only result in a. 03% change in the quantity of beef demanded even though a 1% change in the price of beef will generate a 0. 6% change in the quantity of lamb demanded.

Engle Aggregation Condition n The Engle Aggregation condition states that the sum of all the income elasticities weighted by the proportion of income spent on each good equals 1. For “n” goods” If proportion of income spent on a good changes, then the income elasticities and proportions of incomes spent on the other goods must change to offset it.

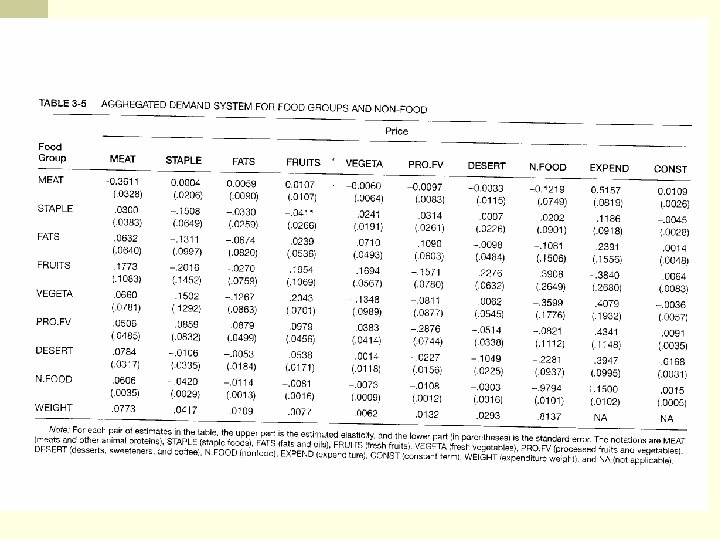
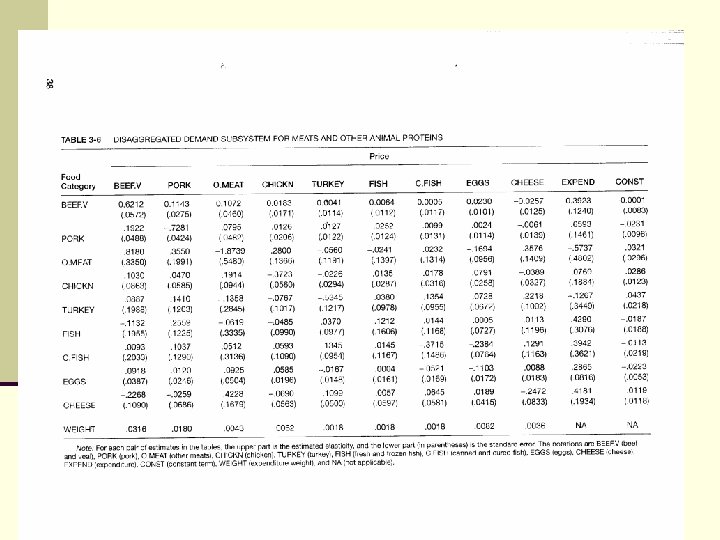
Price Flexibilities n Elasticities assume that Q adjusts to changes in P, but in the case of agricultural commodities, P must typically adjust to what Q is. That is, Q is often fixed during a given production period or, in general, is not able to adjust much in relative terms after a production decision is made. As a result, P must adjust to this Q rather than the other way around. n The responsiveness of P to changes in Q is called the “flexibility. ”

Price Flexibility Cont’ n F = % changes in P as quantity changes. n Flexibilities are useful in studying agricultural commodity markets because supply is often fixed or close to being fixed because: n n n Seasonal nature of supply Perishability Biological lag in reacting to price signals

Relationship Between Flexibilities and Elasticities The flexibility is actually a lower bound for the elasticity

Relationships Among Flexibilities n Demand is inelastic if n Demand is elastic if n Substitutes if n Compliments if