ДЕКАРТОВО ДЕРЕВО дерево пирамида дерамида дерево куча дуча

ДЕКАРТОВО ДЕРЕВО дерево+пирамида = дерамида, дерево+куча = дуча tree+heap = treap Школа олимпиадного программирования 20. 03. 2015

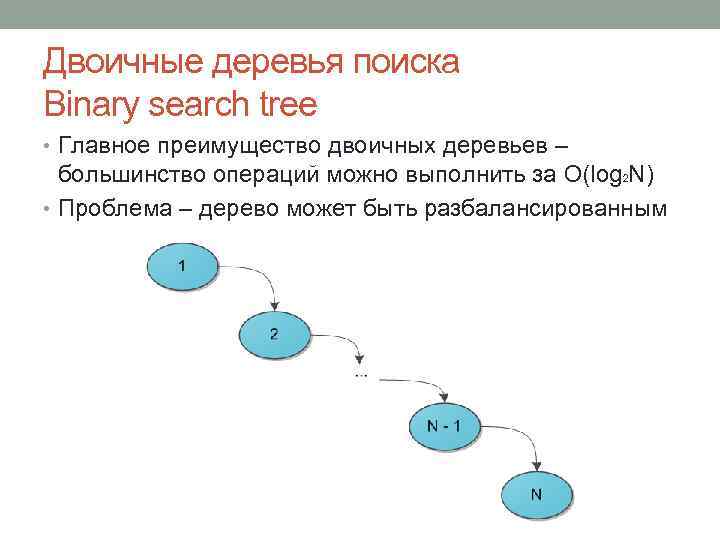Двоичные деревья поиска Binary search tree • Главное преимущество двоичных деревьев – большинство операций можно выполнить за O(log 2 N) • Проблема – дерево может быть разбалансированным

Виды сбалансированных двоичных деревьев • 1) Декартово дерево • 2) Красно-черное дерево • 3) АВЛ-дерево • 4) B-дерево • 5) 2 -3 -дерево • и т. д. • Плюс дерамиды: относительная простота реализации всех операций, все операции выражаются через 2 функции: Split и Merge

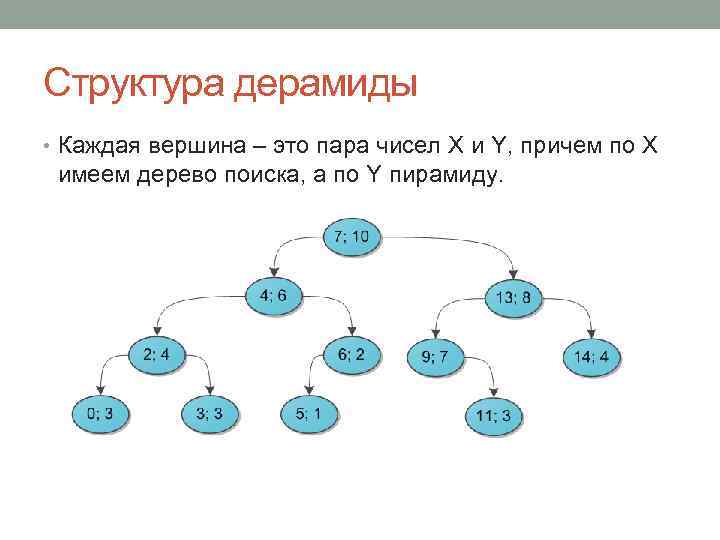Структура дерамиды • Каждая вершина – это пара чисел X и Y, причем по Х имеем дерево поиска, а по Y пирамиду.

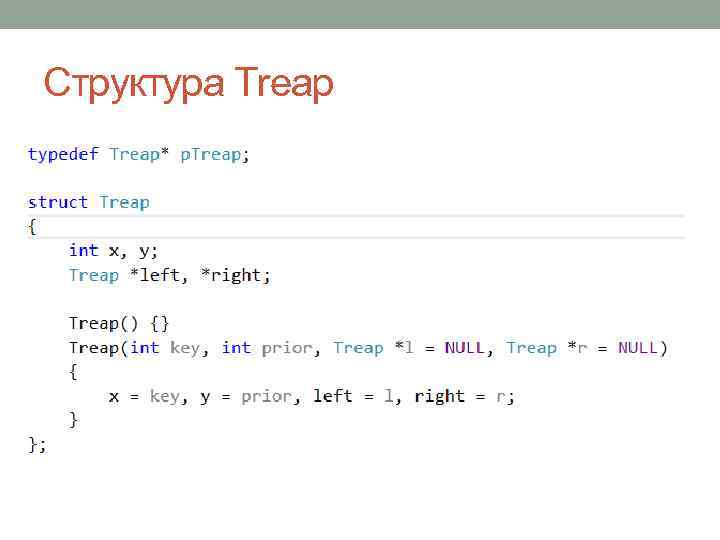Структура Treap

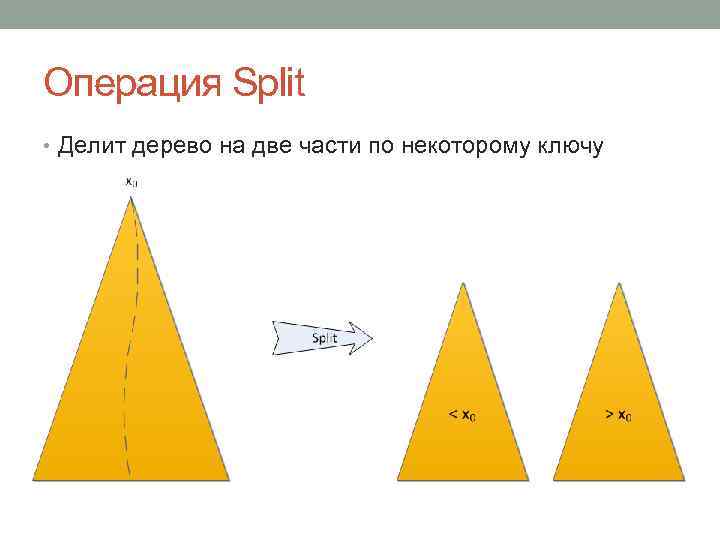Операция Split • Делит дерево на две части по некоторому ключу

Реализация Split

Операция Merge • Объединяет два дерева в одно • Главное условие – ключи(Х) первого дерева должны быть меньше ключей второго

Реализация Merge

Операция Insert • Добавляет в дерево новую вершину с заданным ключом X, приоритет Y выбирается случайно • 1) Делим дерево по ключу X на деревья L и R • 2) Создаем дерево M из одной вершины с ключом X • 3) Объединяем три дерева L, M, R

Реализация Insert

Операция Erase • Удаляет из дерева вершины с ключом равным X • 1) Делим дерево по ключу X-1 на L и R • 2) Делим R по ключу X на M и R • 3) Объединяем L и R, все удаляемые остались в M

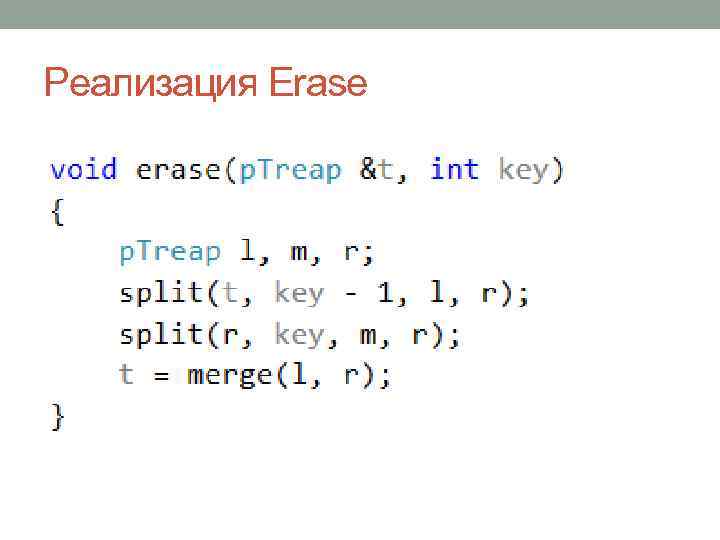Реализация Erase

Операция и реализация Find • Возвращает указатель на вершину в дереве с ключом, равным X, ничем не отличается от обычного дерева поиска

Размеры поддеревьев • Добавим в структура новое поле – size • Функция get. Size будет возвращать размер дерева • Функция recalc будет пересчитывать размер дерева

Получение k-ого по порядку элемента

Сумма на поддереве • Добавим в структуру два поля: • cost – значение в вершине • sum – сумма значений в дереве • В recalc добавим пересчет суммы • get. Sum реализуется аналогично get. Size

Изменение на поддереве • Добавим переменную add в структуру • Применим метод отложенного обновления • Будем вызывать push перед рекурсивными вызовами в split и merge

Литература • • 1) http: //habrahabr. ru/post/101818/ 2) http: //habrahabr. ru/post/102006/ 3) http: //habrahabr. ru/post/102364/ 4) http: //e-maxx. ru/algo/treap Задачи • 1) http: //acm. timus. ru/problem. aspx? space=1&num=2014 • 2) http: //acm. timus. ru/problem. aspx? space=1&num=1890 • 3) http: //ipc. susu. ac. ru/210 -2. html? problem=2040 • 4) http: //ipc. susu. ac. ru/210 -2. html? problem=1969