Декартова прямоугольная система координат в пространстве Прямоугольная

Декартова прямоугольная система координат в пространстве

Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Очень легко и прямо обобщается для пространств любой размерности, что также способствует ее широкому применению. Связанные термины: Декартовой обычно называют прямоугольную систему координат с одинаковыми масштабами по осям, а общей Декартовой системой координат называют аффинную систему координат (не прямоугольную).

• Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющий положение конкретной точки, называется координатами этой точки. • В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.

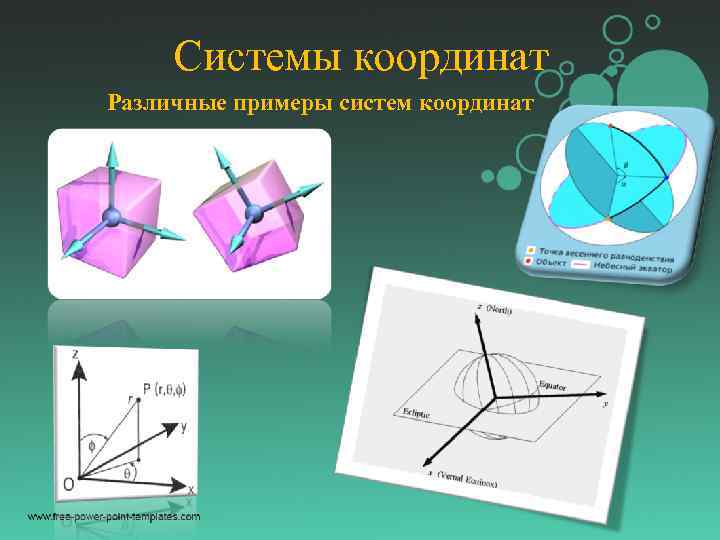Системы координат Различные примеры систем координат

Системы координат • Прямоугольная (Декартова) система координат • Аффинная (косоугольная) система координат • Координаты Риндлера — в пространстве Минковского • Барицентрические координаты • Биангулярные координаты • Полярная система координат • Цилиндрическая система координат • Сферическая система координат • Тороидальная система координат • Параболическая система координат • Параболоидальные координаты • Бицентрические координаты • Биполярные координаты • Бицилиндрические координаты • Биангулярные координаты • Трилинейные координаты • Проективные координаты • Эллипсоидальные координаты (эллиптические координаты) • Конические координаты

Системы координат Прямоугольная (Декартова) система координат Прямоугольная система координат в пространстве (в этом параграфе имеется в виду трехмерное пространство, о более многомерных пространствах — см. ниже) образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O , которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно (не обязательно) одинаковы для всех осей. — OX ось абсцисс, — OY ось ординат, — OZ ось аппликат.

Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y— ординатой точки A, координата z— аппликатой точки A. Символически это записывают так: A(x, y, z) или A=(x, y, z) или привязывают запись координат к конкретной точке с помощью индекса: x. А, y. А, z. А и т. п.

Каждая ось рассматривается как числовая прямая, т. е. имеет положительное направление, а точкам, лежащим на отрицательном луче приписываются отрицательные значения координаты (расстояние берется со знаком минус). То есть, если бы, например, точка лежала не как на рисунке — на луче , а на его продолжении в обратную сторону от точки O (на отрицательной части оси OX), то x, y, z абсцисса x точки A была бы отрицательной (минус расстоянию OB). Аналогично и для двух других осей.

Прямоугольные все системы координат в трехмерном пространстве делятся на два класса — правые (также используются термины положительные, стандартные) и левые. Обычно по умолчанию стараются использовать правые координатные системы, а при их графическом изображении еще и располагать их если можно, в одном из нескольких обычных (традиционных) положений. (На рис. 2 изображена правая координатная система). Правую и левую системы координат невозможно поворотами совместить так, чтобы совпали соответствующие оси (и их направления). Определить, к какому классу относится какая-либо конкретно взятая система координат можно используя правило правой руки, правило винта (положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OX, если этот поворот наблюдать со стороны положительного направления оси OZ).

СП СИБО ЗА А ВНИМАНИЕ!!!