Действительные числа Рациональные числа 1 2 3

Действительные числа

Рациональные числа 1. 2. 3. 4. Множество натуральных чисел (N) – 1, 2, 3, 4, … Целые числа (N + противоположные им числа + 0). (Z) Дробные числа (положительные и отрицательные). Рациональные числа (Целые и дробные) (Q)

Всякое рациональное число, как целое так и дробное, можно представить в виде дроби m-целое число, n – натуральное число

Представить в виде десятичной дроби:

Представить в виде десятичной дроби:

Представить в виде десятичной дроби:

0, 216216… 1. Бесконечная десятичная дробь 2. Периодическая (216 - период) 3. 0, (216) – ноль целых 216 в периоде

Представить в виде десятичной дроби:

Иррациональные числа n n 1) 2) 3) Бесконечные десятичные непериодические дроби (ир отрицание) Примеры: 3, 010012471… - 5, 020022000222… Неизвлекаемые корни:

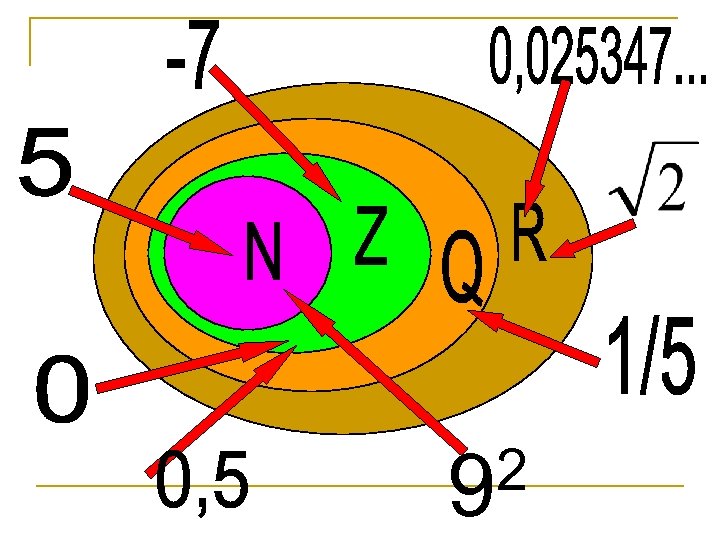
Множество действительных чисел состоит из (R) = Рациональных чисел ( Q ) + Иррациональных чисел (I)

Действительные числа Можно складывать, вычитать, умножать и делить. При выполнении действий над действительными числами в практических задачах их заменяют приближёнными значениями.

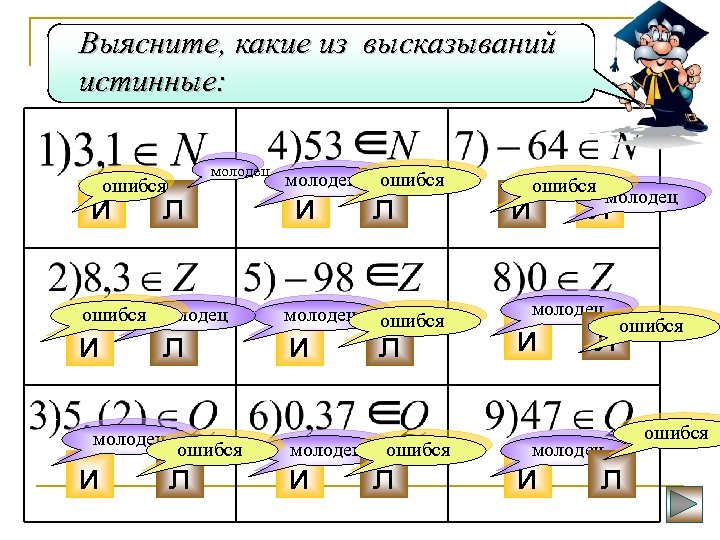Выясните, какие из высказываний истинные: молодец ошибся и л ошибся молодец и л молодец и ошибся л молодец и ошибся л и ошибся молодец л молодец и ошибся л ошибся

2 9

Бесконечные периодические десятичные дроби • 0, (3) или 0, 333… 3333…. 3333333 № 1 представить бесконечную периодическую десятичную дробь 0, (3) в воде обыкновенной Решение: Пусть х = 0, (3) обозначим это уравнение - (*), умножим обе части исходного уравнения на 10 (период), получили уравнение примет вид 10 х = 3, (3) обозначим его - (**) ,

Вычитаем: (**) - (*), получим: 10 х – 1 х = 3, (3) – 0, (3) 9 х = 3 Х= сократив дробь на 3, получим х = Таким образом 0, (3) = .

Бесконечные периодические десятичные дроби • 0, (3) или 0, 253… 3333…. 3333333 № 1 представить бесконечную периодическую десятичную дробь 0, 25(3) в воде обыкновенной Решение: Пусть х = 0, 25(3) умножим обе части исходного уравнения на 100 (до периода), уравнение примет вид 100 х = 25, (3)-обозначим его (*)

Умножим уравнение (*) еще на 10 (период) Получи 1000 х=253, (3) выполним (**) - (*), получим: 1000 х – 100 х = 25 3, (3) – 25, (3) 900 х = 228 Х= сократив дробь на 12, получим х = Таким образом 0, 25(3) = .

№ 2. Представить бесконечную периодическую десятичную дробь в виде обыкновенной (задания (а, б) выполняются у доски с комментариями учащегося и консультацией учителя; задания (в) предназначены для самостоятельной деятельности учащихся). • • • а)1, (23); б)1, (14); в) 2, (16) а)1, 5 (2); б) 1, 3(4); в) 2, 4(3) а)1, 5(23); б)2, 4(13); в) 1, 3(14) а)1, 5(231); б) 2, 1(425); в)2, 1(213) а)1, 52(23); б) 2, 12(24); в) 2, 12(13)