6b0ed62e045f6b42e633f40a0dbdfd61.ppt
- Количество слайдов: 118
 Decisions Under Incomplete Representations & Reasoning Some Reflections Eric Horvitz Microsoft Research SADR Meeting on Decision Making in Complex Environments Cornell University April 5, 2003 horvitz@microsoft. com http: //research. microsoft. com/~horvitz/
Decisions Under Incomplete Representations & Reasoning Some Reflections Eric Horvitz Microsoft Research SADR Meeting on Decision Making in Complex Environments Cornell University April 5, 2003 horvitz@microsoft. com http: //research. microsoft. com/~horvitz/
 Overview n Decision-theoretic systems in the real world – Decision support – Autonomous decision making, embedded processes – Some successes n Decision making under bounded resources – Inference and modeling – Systems immersed in environments Eric Horvitz, April 5, 2003
Overview n Decision-theoretic systems in the real world – Decision support – Autonomous decision making, embedded processes – Some successes n Decision making under bounded resources – Inference and modeling – Systems immersed in environments Eric Horvitz, April 5, 2003
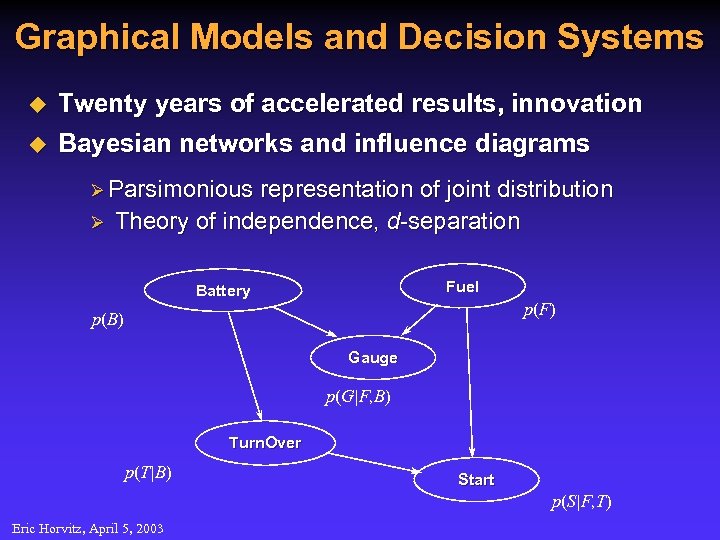 Graphical Models and Decision Systems u Twenty years of accelerated results, innovation u Bayesian networks and influence diagrams Ø Parsimonious Ø representation of joint distribution Theory of independence, d-separation Fuel Battery p(F) p(B) Gauge p(G|F, B) Turn. Over p(T|B) Start p(S|F, T) Eric Horvitz, April 5, 2003
Graphical Models and Decision Systems u Twenty years of accelerated results, innovation u Bayesian networks and influence diagrams Ø Parsimonious Ø representation of joint distribution Theory of independence, d-separation Fuel Battery p(F) p(B) Gauge p(G|F, B) Turn. Over p(T|B) Start p(S|F, T) Eric Horvitz, April 5, 2003
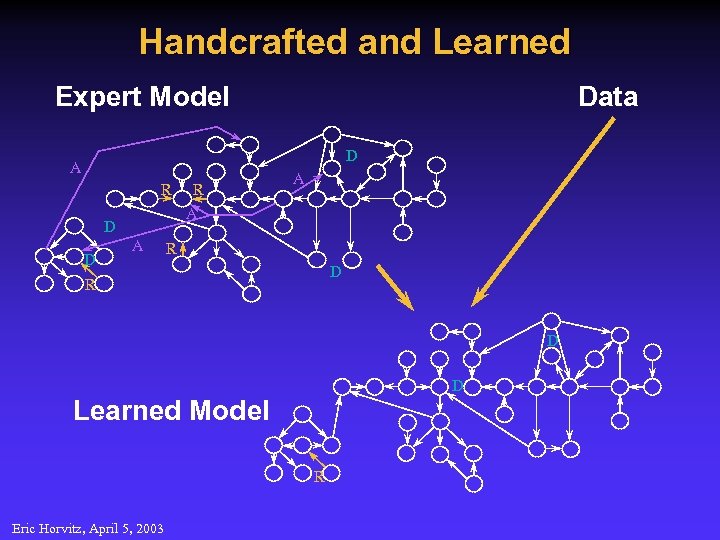 Handcrafted and Learned Expert Model Data D A R D D A R A A R D D Learned Model R Eric Horvitz, April 5, 2003
Handcrafted and Learned Expert Model Data D A R D D A R A A R D D Learned Model R Eric Horvitz, April 5, 2003
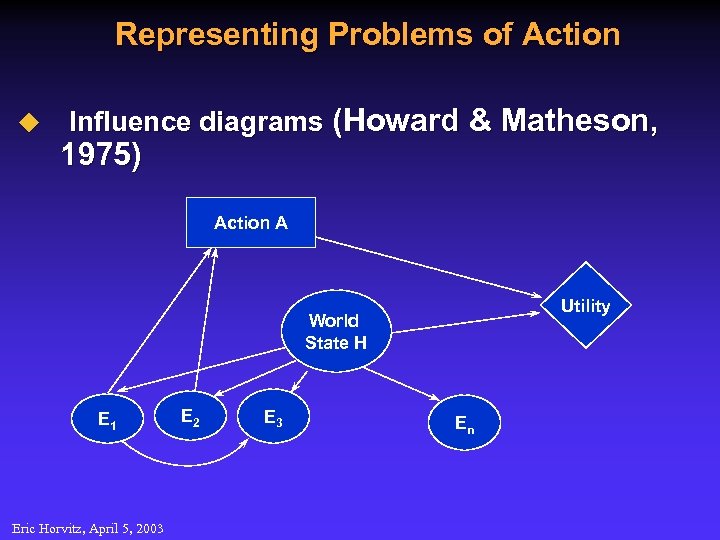 Representing Problems of Action u Influence diagrams (Howard & Matheson, 1975) Action A Utility World State H E 1 Eric Horvitz, April 5, 2003 E 2 E 3 En
Representing Problems of Action u Influence diagrams (Howard & Matheson, 1975) Action A Utility World State H E 1 Eric Horvitz, April 5, 2003 E 2 E 3 En
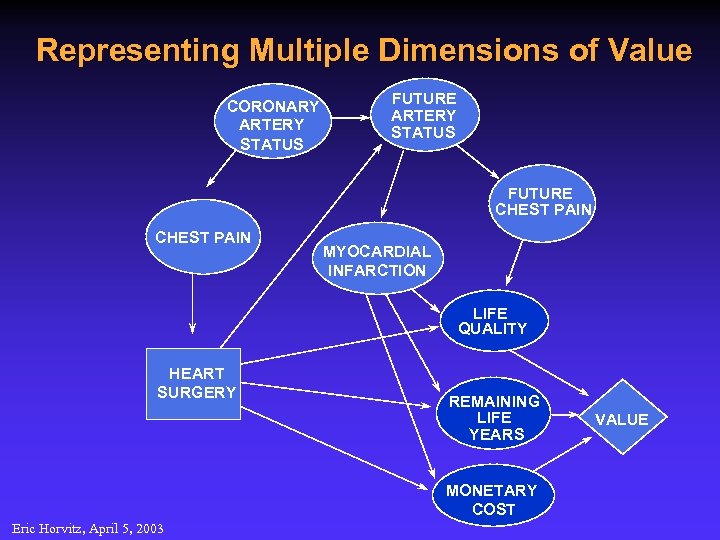 Representing Multiple Dimensions of Value CORONARY ARTERY STATUS FUTURE CHEST PAIN MYOCARDIAL INFARCTION LIFE QUALITY HEART SURGERY REMAINING LIFE YEARS MONETARY COST Eric Horvitz, April 5, 2003 VALUE
Representing Multiple Dimensions of Value CORONARY ARTERY STATUS FUTURE CHEST PAIN MYOCARDIAL INFARCTION LIFE QUALITY HEART SURGERY REMAINING LIFE YEARS MONETARY COST Eric Horvitz, April 5, 2003 VALUE
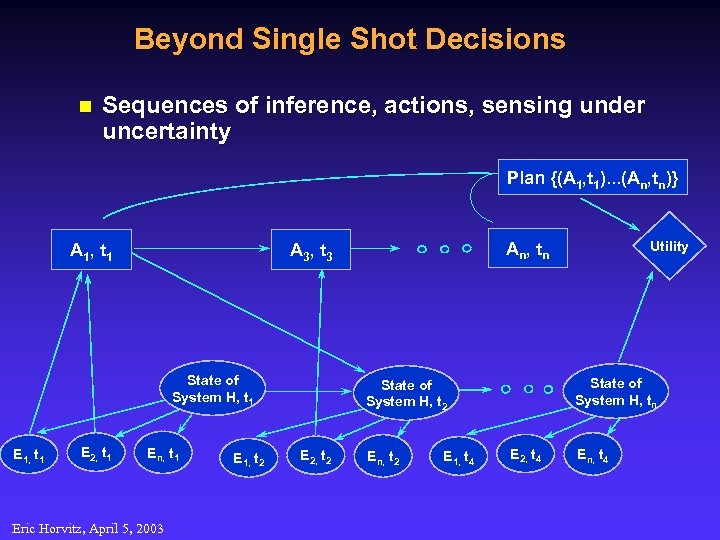 Beyond Single Shot Decisions n Sequences of inference, actions, sensing under uncertainty Plan {(A 1, t 1). . . (An, tn)} State of System H, t 1 E 1, t 1 E 2, t 1 En, t 1 Eric Horvitz, April 5, 2003 E 1, t 2 State of System H, tn State of System H, t 2 E 2, t 2 Utility A n , tn A 3 , t 3 A 1 , t 1 En, t 2 E 1, t 4 E 2, t 4 En, t 4
Beyond Single Shot Decisions n Sequences of inference, actions, sensing under uncertainty Plan {(A 1, t 1). . . (An, tn)} State of System H, t 1 E 1, t 1 E 2, t 1 En, t 1 Eric Horvitz, April 5, 2003 E 1, t 2 State of System H, tn State of System H, t 2 E 2, t 2 Utility A n , tn A 3 , t 3 A 1 , t 1 En, t 2 E 1, t 4 E 2, t 4 En, t 4
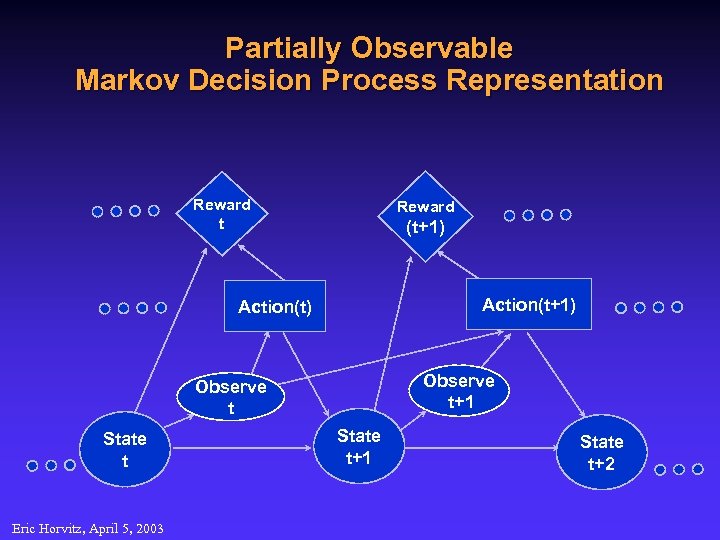 Partially Observable Markov Decision Process Representation Reward t Reward (t+1) Action(t) Observe t+1 Observe t State t Eric Horvitz, April 5, 2003 State t+1 State t+2
Partially Observable Markov Decision Process Representation Reward t Reward (t+1) Action(t) Observe t+1 Observe t State t Eric Horvitz, April 5, 2003 State t+1 State t+2
 Real-World Applications Eric Horvitz, April 5, 2003
Real-World Applications Eric Horvitz, April 5, 2003
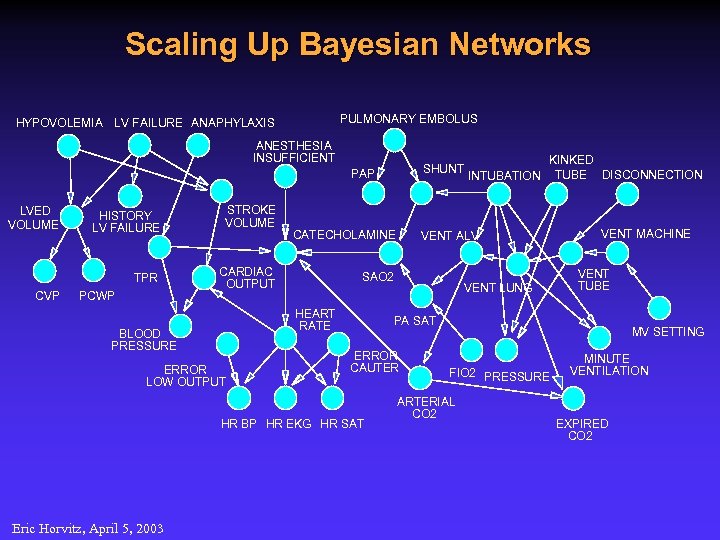 Scaling Up Bayesian Networks PULMONARY EMBOLUS HYPOVOLEMIA LV FAILURE ANAPHYLAXIS ANESTHESIA INSUFFICIENT SHUNT PAP CVP HISTORY LV FAILURE STROKE VOLUME TPR LVED VOLUME CARDIAC OUTPUT PCWP CATECHOLAMINE BLOOD PRESSURE ERROR LOW OUTPUT VENT LUNG VENT MACHINE VENT TUBE PA SAT ERROR CAUTER HR BP HR EKG HR SAT Eric Horvitz, April 5, 2003 KINKED TUBE DISCONNECTION VENT ALV SAO 2 HEART RATE INTUBATION MV SETTING FIO 2 PRESSURE ARTERIAL CO 2 MINUTE VENTILATION EXPIRED CO 2
Scaling Up Bayesian Networks PULMONARY EMBOLUS HYPOVOLEMIA LV FAILURE ANAPHYLAXIS ANESTHESIA INSUFFICIENT SHUNT PAP CVP HISTORY LV FAILURE STROKE VOLUME TPR LVED VOLUME CARDIAC OUTPUT PCWP CATECHOLAMINE BLOOD PRESSURE ERROR LOW OUTPUT VENT LUNG VENT MACHINE VENT TUBE PA SAT ERROR CAUTER HR BP HR EKG HR SAT Eric Horvitz, April 5, 2003 KINKED TUBE DISCONNECTION VENT ALV SAO 2 HEART RATE INTUBATION MV SETTING FIO 2 PRESSURE ARTERIAL CO 2 MINUTE VENTILATION EXPIRED CO 2
 Chief Complaint: Abdominal Pain Eric Horvitz, April 5, 2003
Chief Complaint: Abdominal Pain Eric Horvitz, April 5, 2003
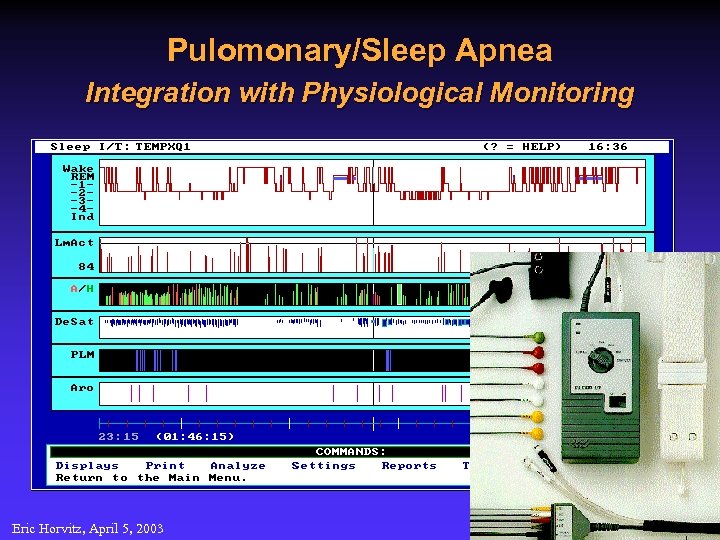 Pulomonary/Sleep Apnea Integration with Physiological Monitoring Eric Horvitz, April 5, 2003
Pulomonary/Sleep Apnea Integration with Physiological Monitoring Eric Horvitz, April 5, 2003
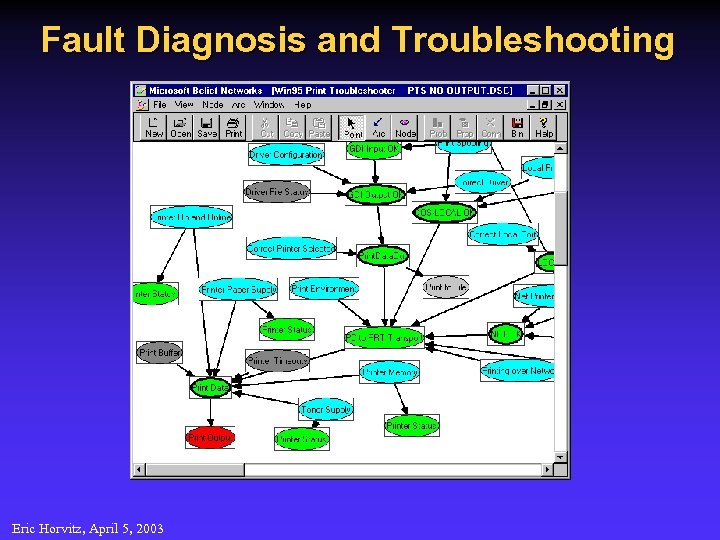 Fault Diagnosis and Troubleshooting Eric Horvitz, April 5, 2003
Fault Diagnosis and Troubleshooting Eric Horvitz, April 5, 2003
 On the Web… www. microsoft. com Eric Horvitz, April 5, 2003
On the Web… www. microsoft. com Eric Horvitz, April 5, 2003
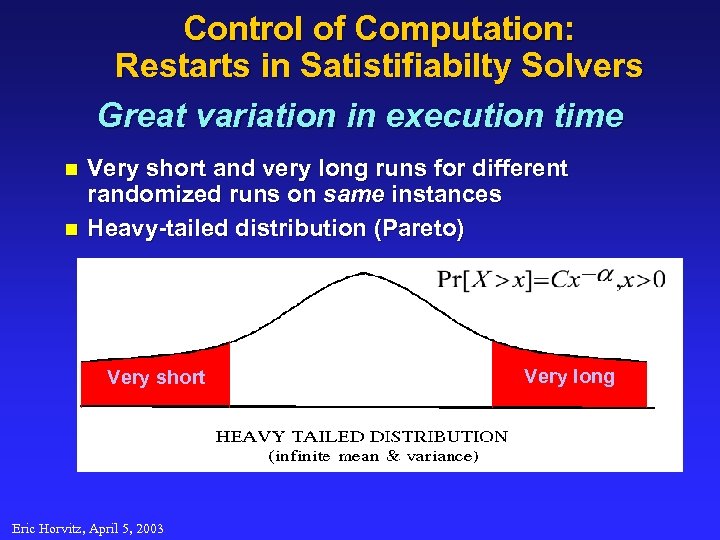 Control of Computation: Restarts in Satistifiabilty Solvers Great variation in execution time n n Very short and very long runs for different randomized runs on same instances Heavy-tailed distribution (Pareto) Very short Eric Horvitz, April 5, 2003 Very long
Control of Computation: Restarts in Satistifiabilty Solvers Great variation in execution time n n Very short and very long runs for different randomized runs on same instances Heavy-tailed distribution (Pareto) Very short Eric Horvitz, April 5, 2003 Very long
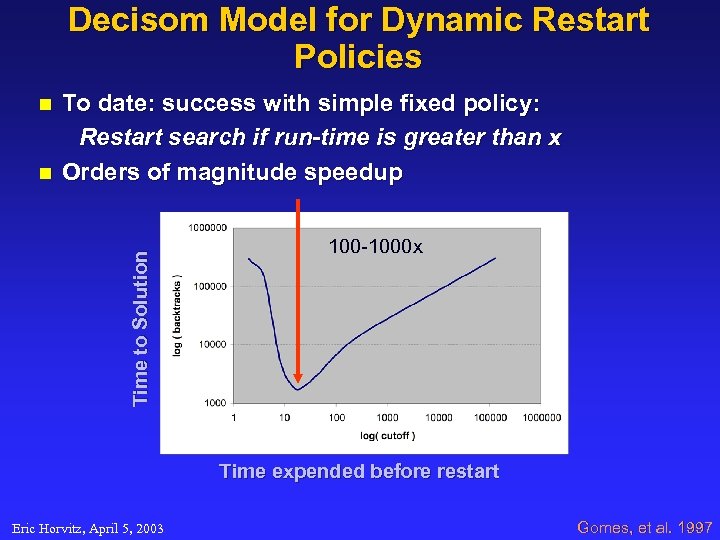 Decisom Model for Dynamic Restart Policies n Time to Solution n To date: success with simple fixed policy: Restart search if run-time is greater than x Orders of magnitude speedup 100 -1000 x Time expended before restart Eric Horvitz, April 5, 2003 Gomes, et al. 1997
Decisom Model for Dynamic Restart Policies n Time to Solution n To date: success with simple fixed policy: Restart search if run-time is greater than x Orders of magnitude speedup 100 -1000 x Time expended before restart Eric Horvitz, April 5, 2003 Gomes, et al. 1997
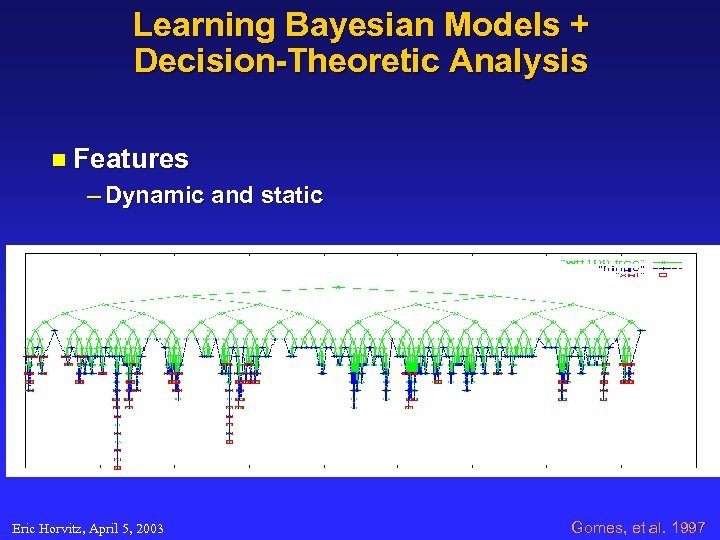 Learning Bayesian Models + Decision-Theoretic Analysis n Features – Dynamic and static Eric Horvitz, April 5, 2003 Gomes, et al. 1997
Learning Bayesian Models + Decision-Theoretic Analysis n Features – Dynamic and static Eric Horvitz, April 5, 2003 Gomes, et al. 1997
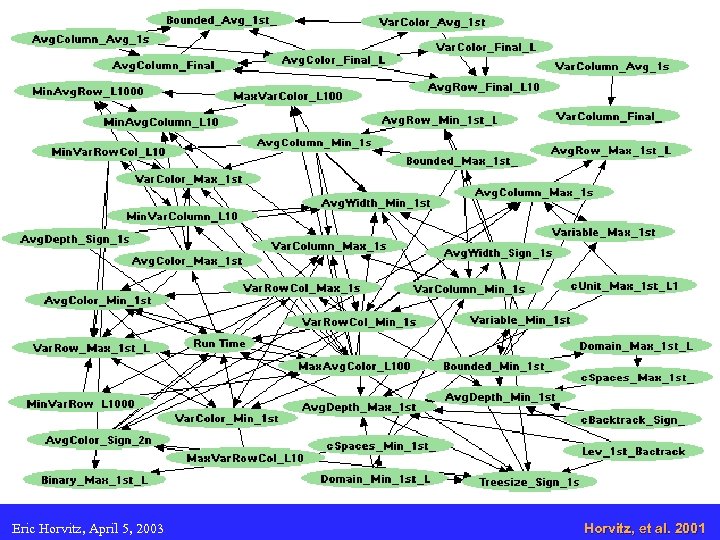 Eric Horvitz, April 5, 2003 Horvitz, et al. 2001
Eric Horvitz, April 5, 2003 Horvitz, et al. 2001
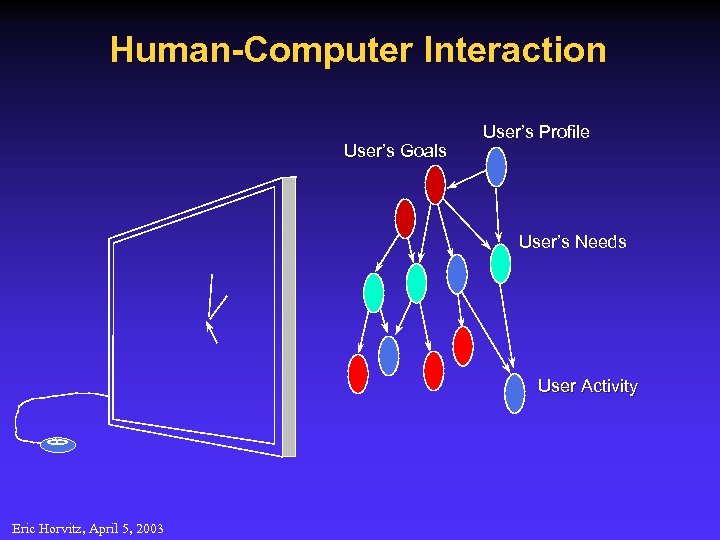 Human-Computer Interaction User’s Goals User’s Profile User’s Needs User Activity Eric Horvitz, April 5, 2003
Human-Computer Interaction User’s Goals User’s Profile User’s Needs User Activity Eric Horvitz, April 5, 2003
 Monitoring Space Shuttle Telemetry Eric Horvitz, April 5, 2003 Horvitz & Barry, 95
Monitoring Space Shuttle Telemetry Eric Horvitz, April 5, 2003 Horvitz & Barry, 95
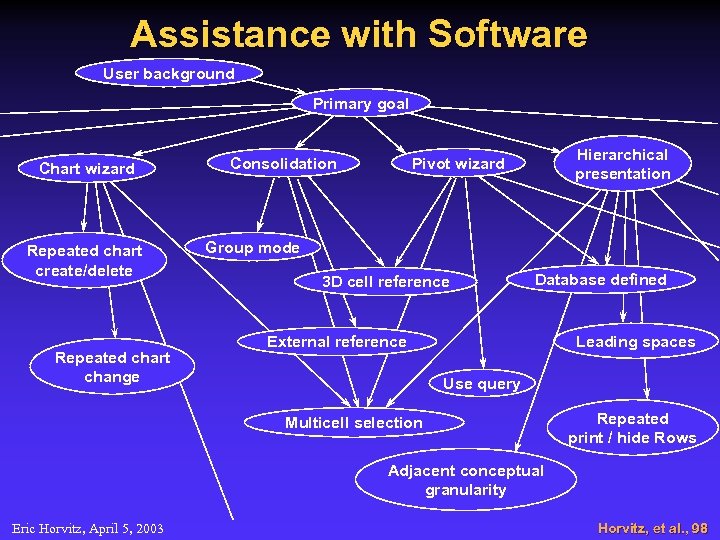 Assistance with Software User background Primary goal Chart wizard Repeated chart create/delete Repeated chart change Consolidation Hierarchical presentation Pivot wizard Group mode 3 D cell reference Database defined Leading spaces External reference Use query Multicell selection Repeated print / hide Rows Adjacent conceptual granularity Eric Horvitz, April 5, 2003 Horvitz, et al. , 98
Assistance with Software User background Primary goal Chart wizard Repeated chart create/delete Repeated chart change Consolidation Hierarchical presentation Pivot wizard Group mode 3 D cell reference Database defined Leading spaces External reference Use query Multicell selection Repeated print / hide Rows Adjacent conceptual granularity Eric Horvitz, April 5, 2003 Horvitz, et al. , 98
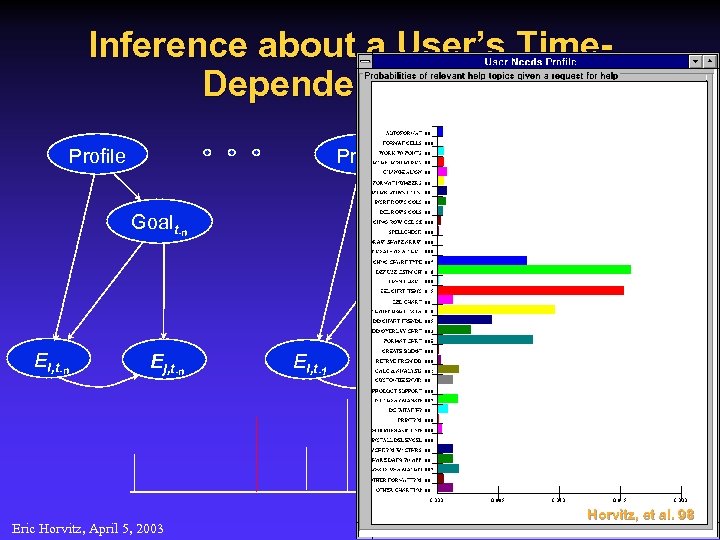 Inference about a User’s Time. Dependent Goals Profile Goalt-n Ei, t-n Profile Ej, t-n Eric Horvitz, April 5, 2003 Goalto Goalt-1 Ei, t-1 Ej, t-1 Ei, to Time Ej, to Horvitz, et al. 98
Inference about a User’s Time. Dependent Goals Profile Goalt-n Ei, t-n Profile Ej, t-n Eric Horvitz, April 5, 2003 Goalto Goalt-1 Ei, t-1 Ej, t-1 Ei, to Time Ej, to Horvitz, et al. 98
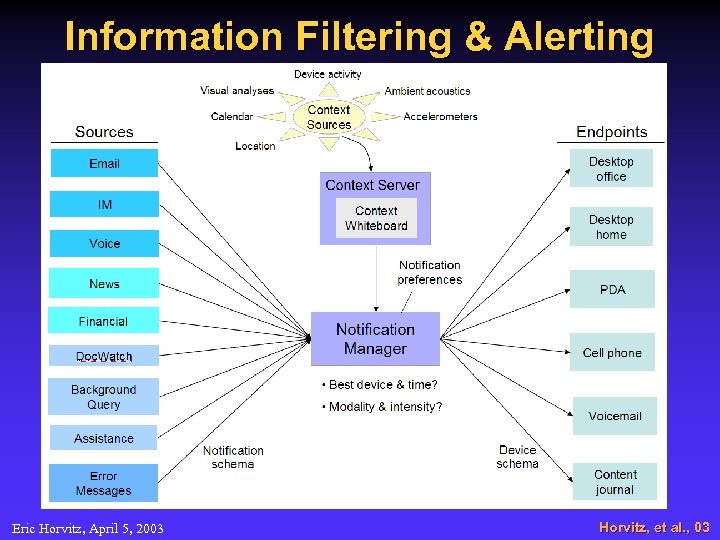 Information Filtering & Alerting Eric Horvitz, April 5, 2003 Horvitz, et al. , 03
Information Filtering & Alerting Eric Horvitz, April 5, 2003 Horvitz, et al. , 03
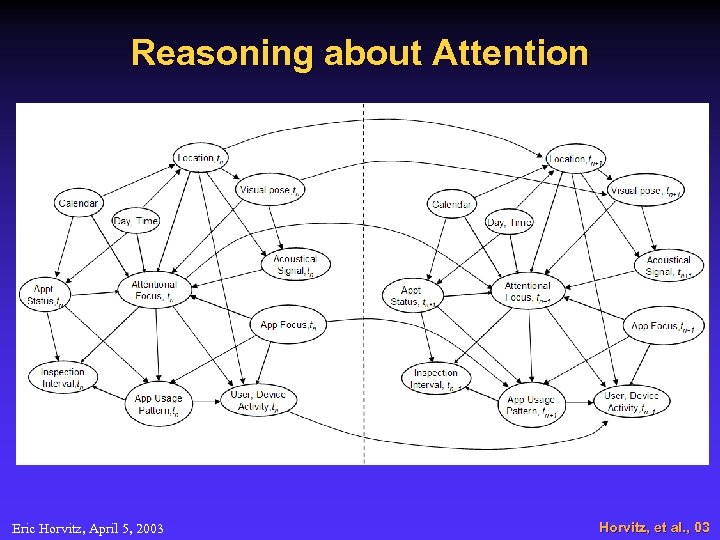 Reasoning about Attention Eric Horvitz, April 5, 2003 Horvitz, et al. , 03
Reasoning about Attention Eric Horvitz, April 5, 2003 Horvitz, et al. , 03
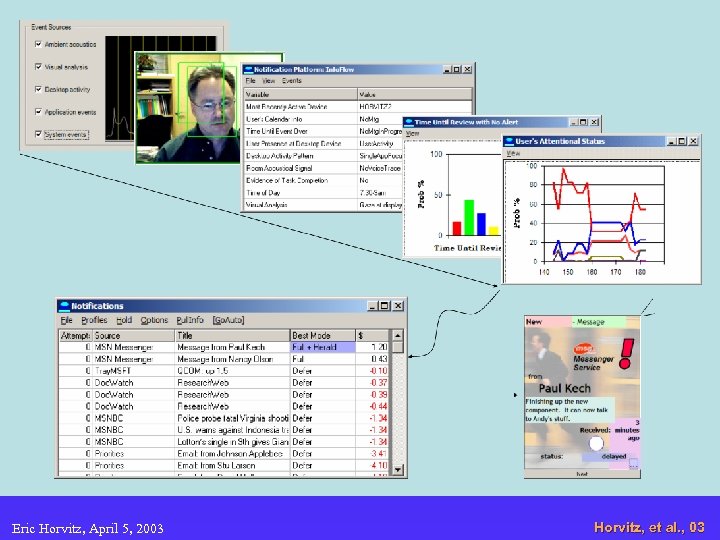 Eric Horvitz, April 5, 2003 Horvitz, et al. , 03
Eric Horvitz, April 5, 2003 Horvitz, et al. , 03
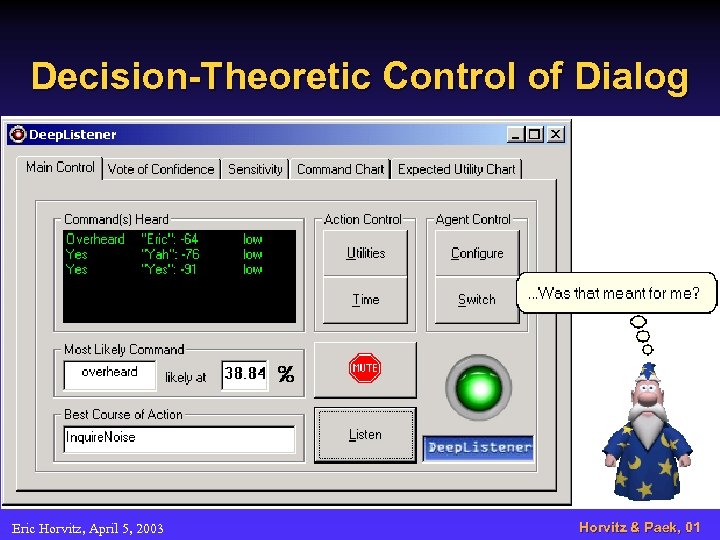 Decision-Theoretic Control of Dialog Eric Horvitz, April 5, 2003 Horvitz & Paek, 01
Decision-Theoretic Control of Dialog Eric Horvitz, April 5, 2003 Horvitz & Paek, 01
 Harnessing Multiple Classes of Evidence u u u Speech recognizer confidence Correctness of natural language parse as evidence Visual analysis of pose Eric Horvitz, April 5, 2003 Paek & Horvitz, 00
Harnessing Multiple Classes of Evidence u u u Speech recognizer confidence Correctness of natural language parse as evidence Visual analysis of pose Eric Horvitz, April 5, 2003 Paek & Horvitz, 00
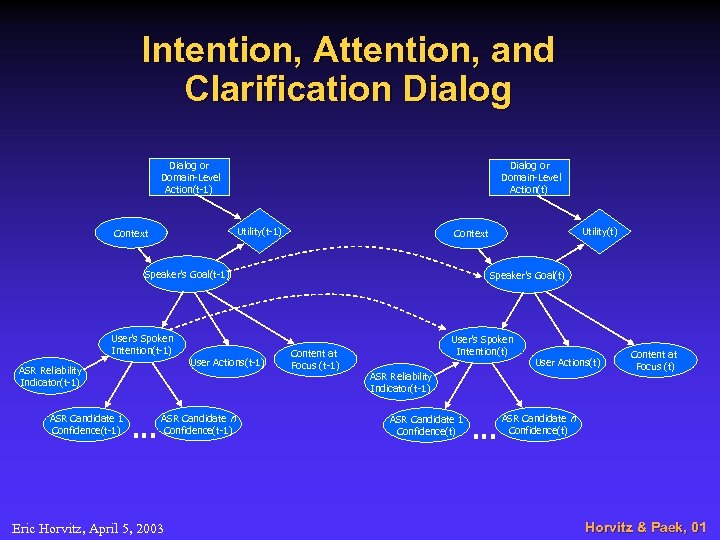 Intention, Attention, and Clarification Dialog or Domain-Level Action(t-1) Dialog or Domain-Level Action(t) Utility(t-1) Context Speaker’s Goal(t-1) User’s Spoken Intention(t-1) ASR Reliability Indicator(t-1) ASR Candidate 1 Confidence(t-1) . . . User Actions(t-1) ASR Candidate n Confidence(t-1) Eric Horvitz, April 5, 2003 Utility(t) Context Speaker’s Goal(t) Content at Focus (t-1) User’s Spoken Intention(t) User Actions(t) ASR Reliability Indicator(t-1) ASR Candidate 1 Confidence(t) . . . Content at Focus (t) ASR Candidate n Confidence(t) Horvitz & Paek, 01
Intention, Attention, and Clarification Dialog or Domain-Level Action(t-1) Dialog or Domain-Level Action(t) Utility(t-1) Context Speaker’s Goal(t-1) User’s Spoken Intention(t-1) ASR Reliability Indicator(t-1) ASR Candidate 1 Confidence(t-1) . . . User Actions(t-1) ASR Candidate n Confidence(t-1) Eric Horvitz, April 5, 2003 Utility(t) Context Speaker’s Goal(t) Content at Focus (t-1) User’s Spoken Intention(t) User Actions(t) ASR Reliability Indicator(t-1) ASR Candidate 1 Confidence(t) . . . Content at Focus (t) ASR Candidate n Confidence(t) Horvitz & Paek, 01
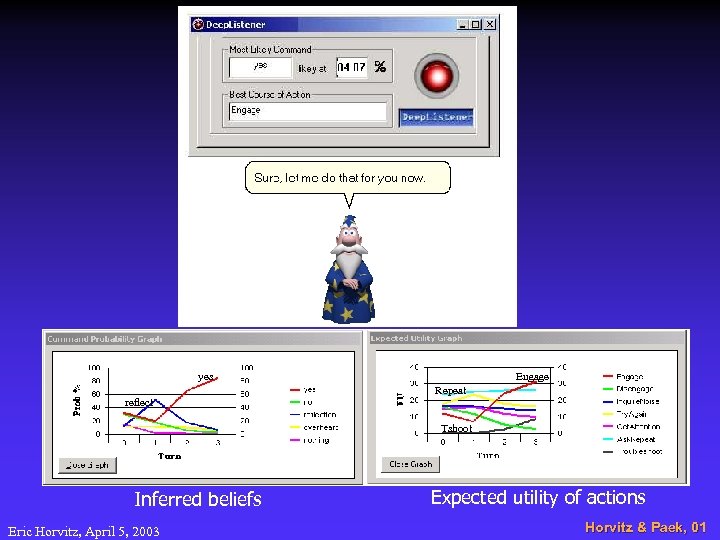 yes reflect Engage Repeat Tshoot Inferred beliefs Eric Horvitz, April 5, 2003 Expected utility of actions Horvitz & Paek, 01
yes reflect Engage Repeat Tshoot Inferred beliefs Eric Horvitz, April 5, 2003 Expected utility of actions Horvitz & Paek, 01
 Interaction Troubleshooting overheard yes Tshoot Repeat no reflect Eric Horvitz, April 5, 2003 Engage Horvitz & Paek, 01
Interaction Troubleshooting overheard yes Tshoot Repeat no reflect Eric Horvitz, April 5, 2003 Engage Horvitz & Paek, 01
 Assessing Preferences on Outcomes Eric Horvitz, April 5, 2003 Horvitz & Paek, 01
Assessing Preferences on Outcomes Eric Horvitz, April 5, 2003 Horvitz & Paek, 01
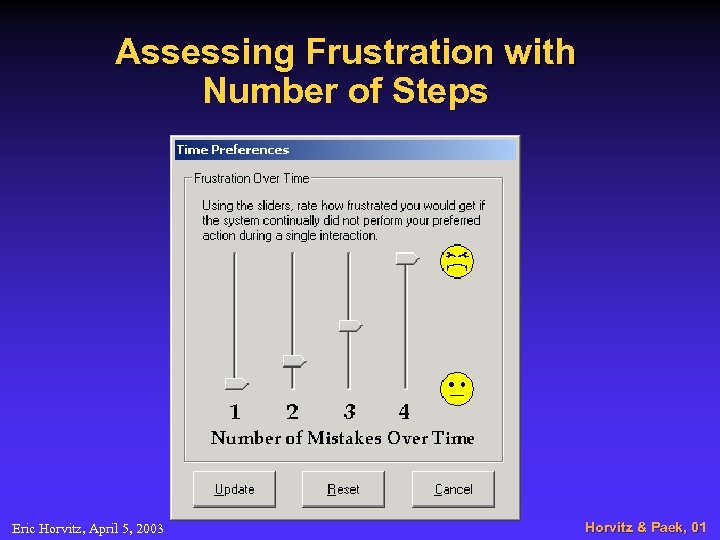 Assessing Frustration with Number of Steps Eric Horvitz, April 5, 2003 Horvitz & Paek, 01
Assessing Frustration with Number of Steps Eric Horvitz, April 5, 2003 Horvitz & Paek, 01
 But Still Cannot Solve Important Problems u u u Intractability per problem size and structure Little experience with fielding autonomous, immersed decision making systems Poor understanding of subobtimality associated with incomplete models and inference Toward principles of rational action under resource limitations Eric Horvitz, April 5, 2003
But Still Cannot Solve Important Problems u u u Intractability per problem size and structure Little experience with fielding autonomous, immersed decision making systems Poor understanding of subobtimality associated with incomplete models and inference Toward principles of rational action under resource limitations Eric Horvitz, April 5, 2003
 Hardness u Inference is NP-Hard; approximation is NP-Hard u Work on a tapestry of exact and approximate algorithms u Exploit special structure, probe portions of model, restricted probabilistic relationships Eric Horvitz, April 5, 2003
Hardness u Inference is NP-Hard; approximation is NP-Hard u Work on a tapestry of exact and approximate algorithms u Exploit special structure, probe portions of model, restricted probabilistic relationships Eric Horvitz, April 5, 2003
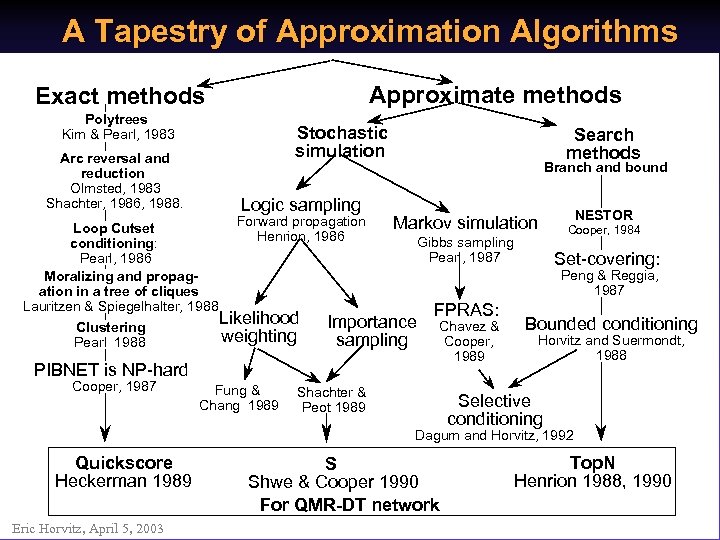 A Tapestry of Approximation Algorithms Approximate methods Exact methods Polytrees Kim & Pearl, 1983 Arc reversal and reduction Olmsted, 1983 Shachter, 1986, 1988. Stochastic simulation Logic sampling Forward propagation Henrion, 1986 Loop Cutset conditioning: Pearl, 1986 Moralizing and propagation in a tree of cliques Lauritzen & Spiegelhalter, 1988 Likelihood Clustering weighting Pearl 1988 Fung & Chang 1989 Branch and bound Markov simulation Gibbs sampling Pearl, 1987 NESTOR Cooper, 1984 Set-covering: Peng & Reggia, 1987 Importance sampling PIBNET is NP-hard Cooper, 1987 Search methods FPRAS: Chavez & Cooper, 1989 Shachter & Peot 1989 Bounded conditioning Horvitz and Suermondt, 1988 Selective conditioning Dagum and Horvitz, 1992 Quickscore Heckerman 1989 Eric Horvitz, April 5, 2003 S Shwe & Cooper 1990 For QMR-DT network Top. N Henrion 1988, 1990
A Tapestry of Approximation Algorithms Approximate methods Exact methods Polytrees Kim & Pearl, 1983 Arc reversal and reduction Olmsted, 1983 Shachter, 1986, 1988. Stochastic simulation Logic sampling Forward propagation Henrion, 1986 Loop Cutset conditioning: Pearl, 1986 Moralizing and propagation in a tree of cliques Lauritzen & Spiegelhalter, 1988 Likelihood Clustering weighting Pearl 1988 Fung & Chang 1989 Branch and bound Markov simulation Gibbs sampling Pearl, 1987 NESTOR Cooper, 1984 Set-covering: Peng & Reggia, 1987 Importance sampling PIBNET is NP-hard Cooper, 1987 Search methods FPRAS: Chavez & Cooper, 1989 Shachter & Peot 1989 Bounded conditioning Horvitz and Suermondt, 1988 Selective conditioning Dagum and Horvitz, 1992 Quickscore Heckerman 1989 Eric Horvitz, April 5, 2003 S Shwe & Cooper 1990 For QMR-DT network Top. N Henrion 1988, 1990
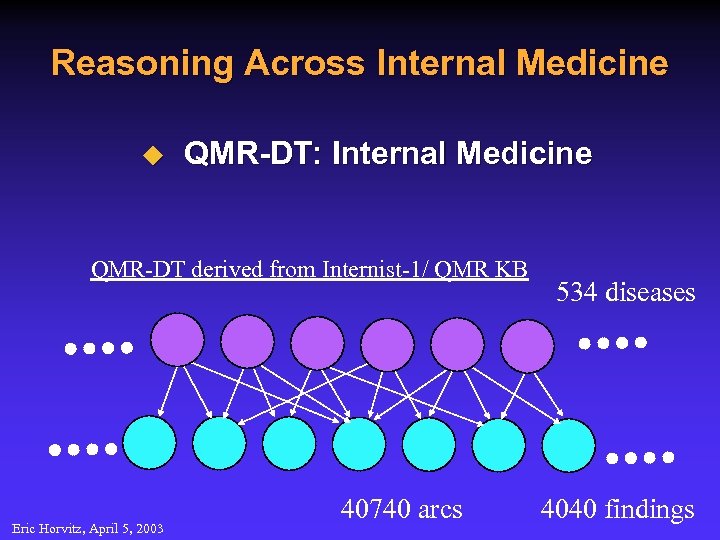 Reasoning Across Internal Medicine u QMR-DT: Internal Medicine QMR-DT derived from Internist-1/ QMR KB Eric Horvitz, April 5, 2003 40740 arcs 534 diseases 4040 findings
Reasoning Across Internal Medicine u QMR-DT: Internal Medicine QMR-DT derived from Internist-1/ QMR KB Eric Horvitz, April 5, 2003 40740 arcs 534 diseases 4040 findings
 Toward Principles n What do we do when we cannot solve a decision problem completely? n How do we trade computation time and value of computation? n What is a complete problem? n How do we reason about sensitivity of the MEU of action to refinement effort? n Toward principles of decisions under bounded resources – Simon: Inadequacy of MEU – Good: Type II Rationality Eric Horvitz, April 5, 2003
Toward Principles n What do we do when we cannot solve a decision problem completely? n How do we trade computation time and value of computation? n What is a complete problem? n How do we reason about sensitivity of the MEU of action to refinement effort? n Toward principles of decisions under bounded resources – Simon: Inadequacy of MEU – Good: Type II Rationality Eric Horvitz, April 5, 2003
 Implementing Type II Rationality Under Limited Resources n Need tractable meta-analysis of ideal nature and extent of reasoning n Need characterizable approximation methods n Need good understanding of cost of time, memory Eric Horvitz, April 5, 2003
Implementing Type II Rationality Under Limited Resources n Need tractable meta-analysis of ideal nature and extent of reasoning n Need characterizable approximation methods n Need good understanding of cost of time, memory Eric Horvitz, April 5, 2003
 Understanding Cost of Computation n “Cost: ” “… … - C(t)” n Influence of specific classes of cost on value of computation, comprehensive value of ultimate action n Active inference about the structure of cost, expectation Eric Horvitz, April 5, 2003
Understanding Cost of Computation n “Cost: ” “… … - C(t)” n Influence of specific classes of cost on value of computation, comprehensive value of ultimate action n Active inference about the structure of cost, expectation Eric Horvitz, April 5, 2003
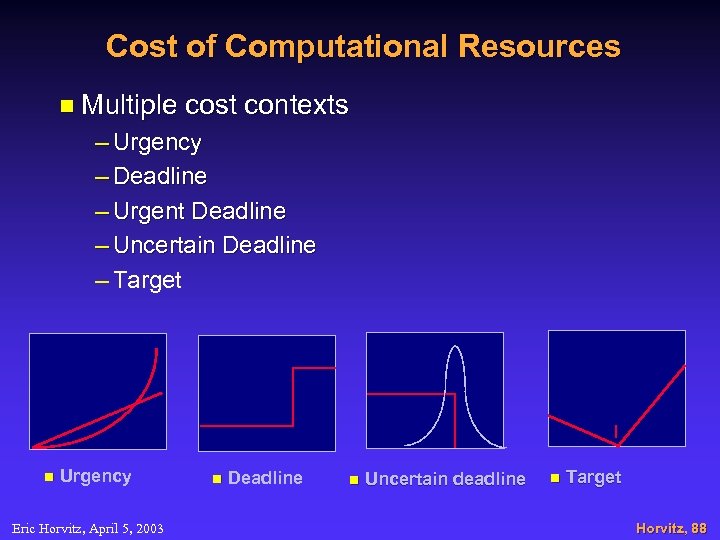 Cost of Computational Resources n Multiple cost contexts – Urgency – Deadline – Urgent Deadline – Uncertain Deadline – Target n Urgency Eric Horvitz, April 5, 2003 n Deadline n Uncertain deadline n Target Horvitz, 88
Cost of Computational Resources n Multiple cost contexts – Urgency – Deadline – Urgent Deadline – Uncertain Deadline – Target n Urgency Eric Horvitz, April 5, 2003 n Deadline n Uncertain deadline n Target Horvitz, 88
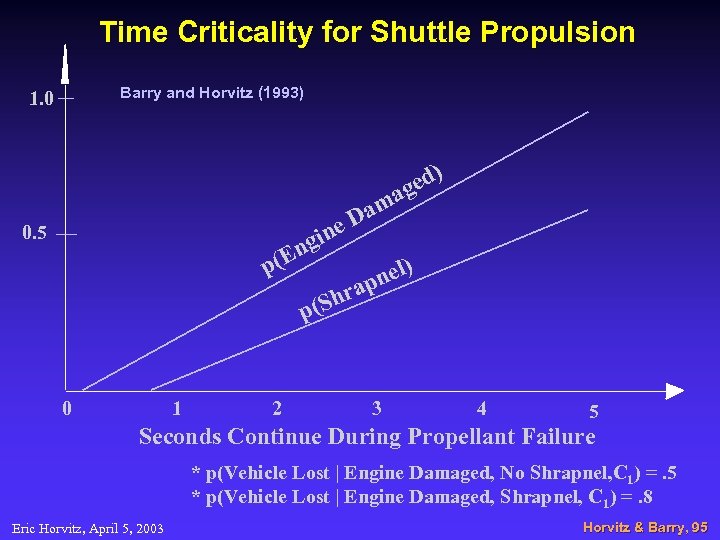 Time Criticality for Shuttle Propulsion Barry and Horvitz (1993) 1. 0 ed) ag am e. D in 0. 5 ng (E p 0 1 2 ) l pne a r (Sh p 3 4 5 Seconds Continue During Propellant Failure * p(Vehicle Lost | Engine Damaged, No Shrapnel, C 1) =. 5 * p(Vehicle Lost | Engine Damaged, Shrapnel, C 1) =. 8 Eric Horvitz, April 5, 2003 Horvitz & Barry, 95
Time Criticality for Shuttle Propulsion Barry and Horvitz (1993) 1. 0 ed) ag am e. D in 0. 5 ng (E p 0 1 2 ) l pne a r (Sh p 3 4 5 Seconds Continue During Propellant Failure * p(Vehicle Lost | Engine Damaged, No Shrapnel, C 1) =. 5 * p(Vehicle Lost | Engine Damaged, Shrapnel, C 1) =. 8 Eric Horvitz, April 5, 2003 Horvitz & Barry, 95
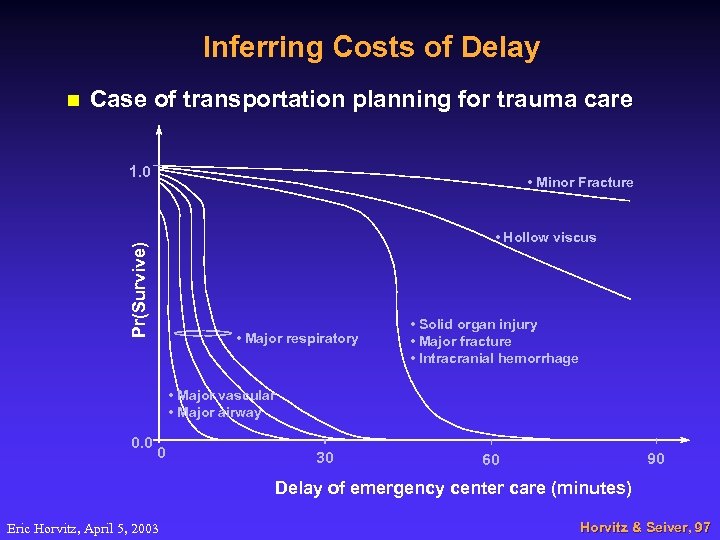 Inferring Costs of Delay n Case of transportation planning for trauma care 1. 0 • Minor Fracture Pr(Survive) • Hollow viscus • Major respiratory • Solid organ injury • Major fracture • Intracranial hemorrhage • Major vascular • Major airway 0. 0 0 30 90 60 Delay of emergency center care (minutes) Eric Horvitz, April 5, 2003 Horvitz & Seiver, 97
Inferring Costs of Delay n Case of transportation planning for trauma care 1. 0 • Minor Fracture Pr(Survive) • Hollow viscus • Major respiratory • Solid organ injury • Major fracture • Intracranial hemorrhage • Major vascular • Major airway 0. 0 0 30 90 60 Delay of emergency center care (minutes) Eric Horvitz, April 5, 2003 Horvitz & Seiver, 97
 Context-Sensitive Costs Eric Horvitz, April 5, 2003 Horvitz & Seiver, 97
Context-Sensitive Costs Eric Horvitz, April 5, 2003 Horvitz & Seiver, 97
 Characterizing the Value of Computation Eric Horvitz, April 5, 2003
Characterizing the Value of Computation Eric Horvitz, April 5, 2003
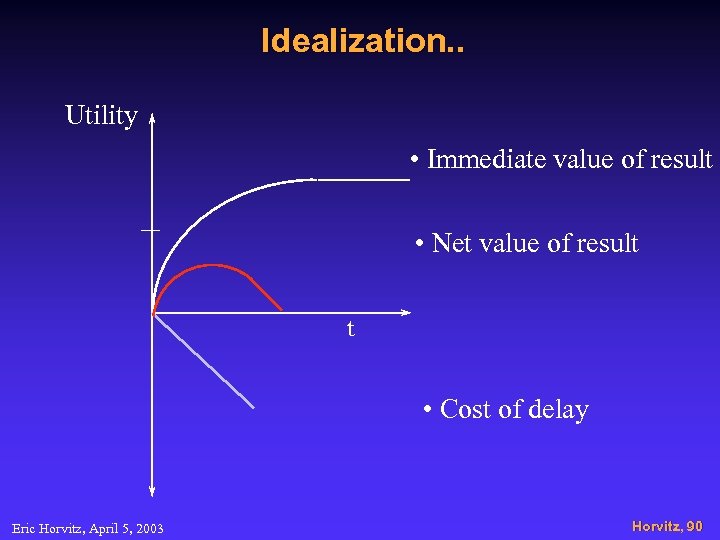 Idealization. . Utility • Immediate value of result • Net value of result t • Cost of delay Eric Horvitz, April 5, 2003 Horvitz, 90
Idealization. . Utility • Immediate value of result • Net value of result t • Cost of delay Eric Horvitz, April 5, 2003 Horvitz, 90
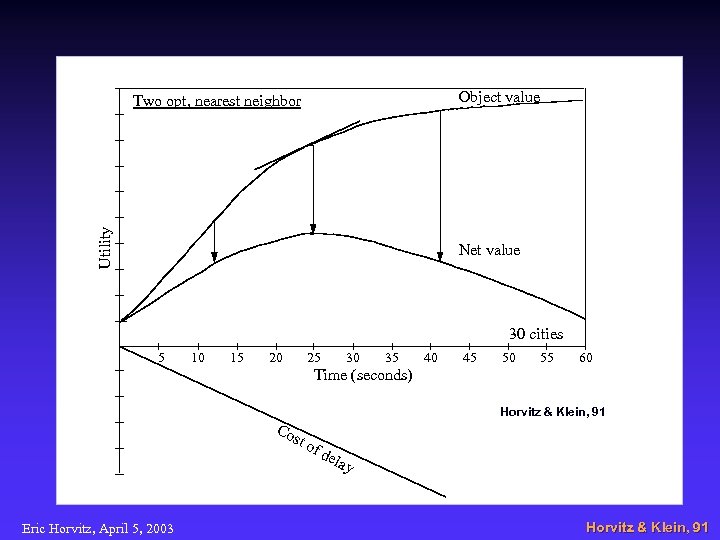 Object value Two opt, nearest neighbor • Utility • Net value 30 cities 5 10 15 20 25 30 35 40 45 50 55 60 Time (seconds) Co Horvitz & Klein, 91 st o Eric Horvitz, April 5, 2003 fd ela y Horvitz & Klein, 91
Object value Two opt, nearest neighbor • Utility • Net value 30 cities 5 10 15 20 25 30 35 40 45 50 55 60 Time (seconds) Co Horvitz & Klein, 91 st o Eric Horvitz, April 5, 2003 fd ela y Horvitz & Klein, 91
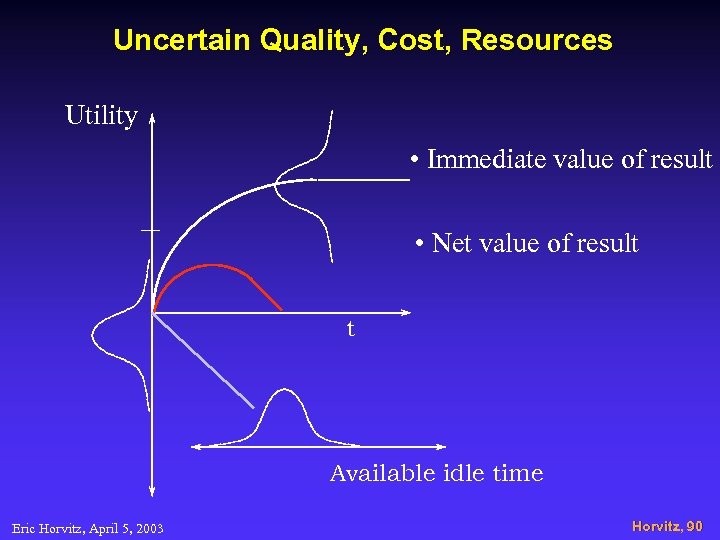 Uncertain Quality, Cost, Resources Utility • Immediate value of result • Net value of result t Available idle time Eric Horvitz, April 5, 2003 Horvitz, 90
Uncertain Quality, Cost, Resources Utility • Immediate value of result • Net value of result t Available idle time Eric Horvitz, April 5, 2003 Horvitz, 90
 Models of Type II Rationality Example: Acute Respiratory Failure (ARF) vs. Respiratory Distress (RD) Eric Horvitz, April 5, 2003 Horvitz, 90
Models of Type II Rationality Example: Acute Respiratory Failure (ARF) vs. Respiratory Distress (RD) Eric Horvitz, April 5, 2003 Horvitz, 90
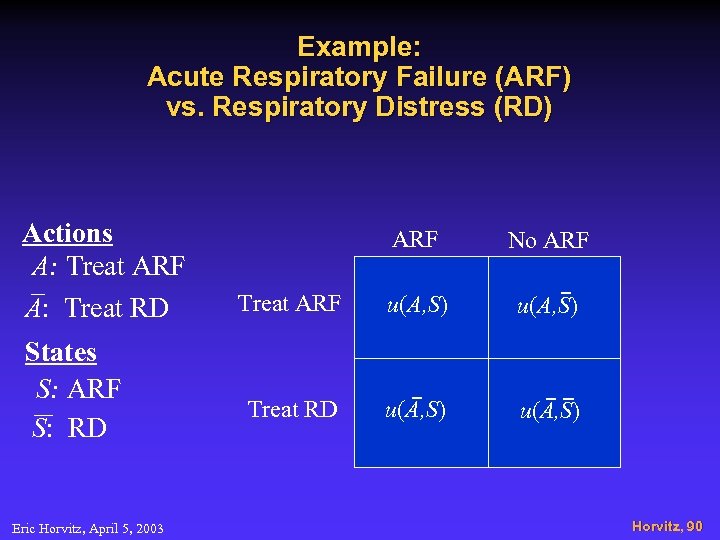 Example: Acute Respiratory Failure (ARF) vs. Respiratory Distress (RD) Actions A: Treat ARF A: Treat RD States S: ARF S: RD Eric Horvitz, April 5, 2003 ARF No ARF Treat ARF u(A, S) Treat RD u(A, S) Horvitz, 90
Example: Acute Respiratory Failure (ARF) vs. Respiratory Distress (RD) Actions A: Treat ARF A: Treat RD States S: ARF S: RD Eric Horvitz, April 5, 2003 ARF No ARF Treat ARF u(A, S) Treat RD u(A, S) Horvitz, 90
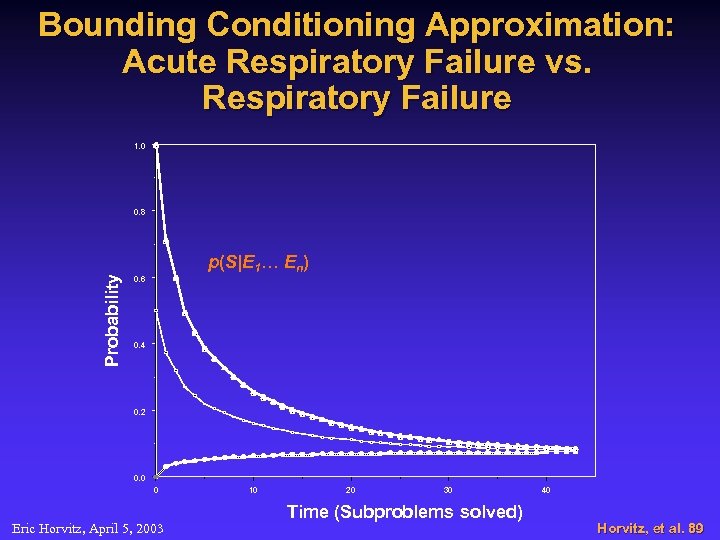 Bounding Conditioning Approximation: Acute Respiratory Failure vs. Respiratory Failure 1. 0 Probability 0. 8 p(S|E 1… En) 0. 6 0. 4 0. 2 0. 0 0 Eric Horvitz, April 5, 2003 10 20 30 Time (Subproblems solved) 40 Horvitz, et al. 89
Bounding Conditioning Approximation: Acute Respiratory Failure vs. Respiratory Failure 1. 0 Probability 0. 8 p(S|E 1… En) 0. 6 0. 4 0. 2 0. 0 0 Eric Horvitz, April 5, 2003 10 20 30 Time (Subproblems solved) 40 Horvitz, et al. 89
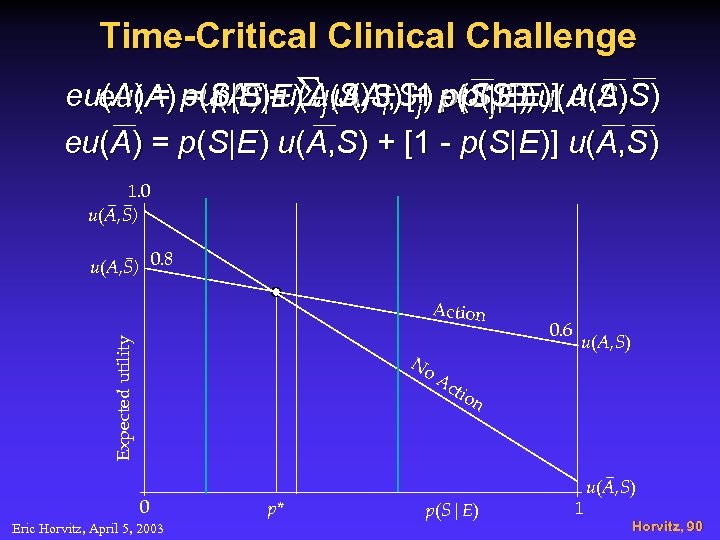 Time-Critical Clinical Challenge eueu)A) p(SA))= )(A, u()S, )S+ p((S|j. S|)) u(A(S)S) (A( = eup|E |E Sj (S A+ [1 - p( |EE)] u, A, = ( (S u u A , i j ) p S E eu(A) = p(S|E) u(A, S) + [1 - p(S|E)] u(A, S) 1. 0 u(A, S) 0. 8 Expected utility Action No 0 Eric Horvitz, April 5, 2003 p* 0. 6 u(A, S) Ac tio n p(S|E) 1 u(A, S) Horvitz, 90
Time-Critical Clinical Challenge eueu)A) p(SA))= )(A, u()S, )S+ p((S|j. S|)) u(A(S)S) (A( = eup|E |E Sj (S A+ [1 - p( |EE)] u, A, = ( (S u u A , i j ) p S E eu(A) = p(S|E) u(A, S) + [1 - p(S|E)] u(A, S) 1. 0 u(A, S) 0. 8 Expected utility Action No 0 Eric Horvitz, April 5, 2003 p* 0. 6 u(A, S) Ac tio n p(S|E) 1 u(A, S) Horvitz, 90
![Time-Critical Clinical Challenge eu(A, t) = p(S|E) u(A, S, t) + [1 - p(S|E)] Time-Critical Clinical Challenge eu(A, t) = p(S|E) u(A, S, t) + [1 - p(S|E)]](https://present5.com/presentation/6b0ed62e045f6b42e633f40a0dbdfd61/image-52.jpg) Time-Critical Clinical Challenge eu(A, t) = p(S|E) u(A, S, t) + [1 - p(S|E)] u(A, S) eu(A) = p(S|E) u(A, S) + [1 - p(S|E)] u(A, S) 1. 0 u(A, S) 0. 8 Expected utility Action No 0 Eric Horvitz, April 5, 2003 p* 0. 6 u(A, S) Ac tio n p(S|E) 1 u(A, S) Horvitz, 90
Time-Critical Clinical Challenge eu(A, t) = p(S|E) u(A, S, t) + [1 - p(S|E)] u(A, S) eu(A) = p(S|E) u(A, S) + [1 - p(S|E)] u(A, S) 1. 0 u(A, S) 0. 8 Expected utility Action No 0 Eric Horvitz, April 5, 2003 p* 0. 6 u(A, S) Ac tio n p(S|E) 1 u(A, S) Horvitz, 90
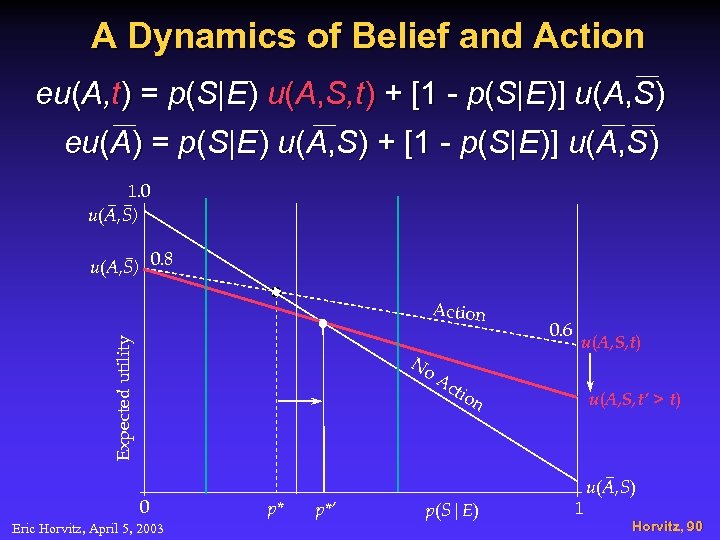 A Dynamics of Belief and Action eu(A, t) = p(S|E) u(A, S, t) + [1 - p(S|E)] u(A, S) eu(A) = p(S|E) u(A, S) + [1 - p(S|E)] u(A, S) 1. 0 u(A, S) 0. 8 Expected utility Action No 0 Eric Horvitz, April 5, 2003 p* p*’ 0. 6 u(A, S, t) Ac tio n p(S|E) u(A, S, t’ > t) 1 u(A, S) Horvitz, 90
A Dynamics of Belief and Action eu(A, t) = p(S|E) u(A, S, t) + [1 - p(S|E)] u(A, S) eu(A) = p(S|E) u(A, S) + [1 - p(S|E)] u(A, S) 1. 0 u(A, S) 0. 8 Expected utility Action No 0 Eric Horvitz, April 5, 2003 p* p*’ 0. 6 u(A, S, t) Ac tio n p(S|E) u(A, S, t’ > t) 1 u(A, S) Horvitz, 90
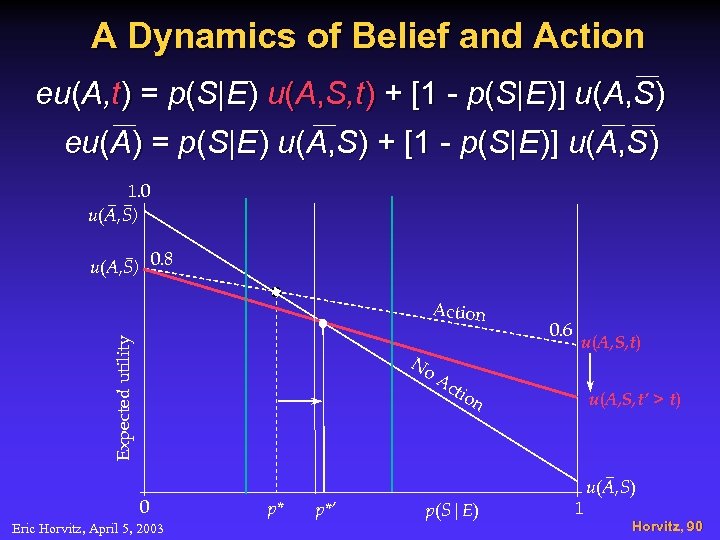 A Dynamics of Belief and Action eu(A, t) = p(S|E) u(A, S, t) + [1 - p(S|E)] u(A, S) eu(A) = p(S|E) u(A, S) + [1 - p(S|E)] u(A, S) 1. 0 u(A, S) 0. 8 Expected utility Action No 0 Eric Horvitz, April 5, 2003 p* p*’ 0. 6 u(A, S, t) Ac tio n p(S|E) u(A, S, t’ > t) 1 u(A, S) Horvitz, 90
A Dynamics of Belief and Action eu(A, t) = p(S|E) u(A, S, t) + [1 - p(S|E)] u(A, S) eu(A) = p(S|E) u(A, S) + [1 - p(S|E)] u(A, S) 1. 0 u(A, S) 0. 8 Expected utility Action No 0 Eric Horvitz, April 5, 2003 p* p*’ 0. 6 u(A, S, t) Ac tio n p(S|E) u(A, S, t’ > t) 1 u(A, S) Horvitz, 90
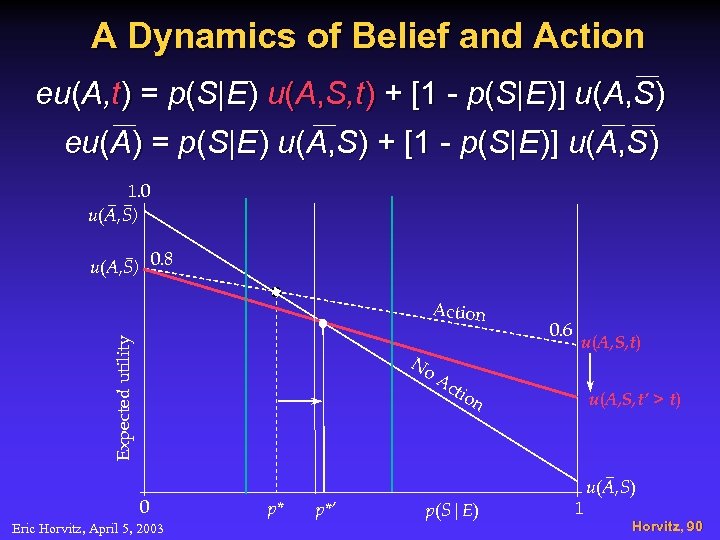 A Dynamics of Belief and Action eu(A, t) = p(S|E) u(A, S, t) + [1 - p(S|E)] u(A, S) eu(A) = p(S|E) u(A, S) + [1 - p(S|E)] u(A, S) 1. 0 u(A, S) 0. 8 Expected utility Action No 0 Eric Horvitz, April 5, 2003 p* p*’ 0. 6 u(A, S, t) Ac tio n p(S|E) u(A, S, t’ > t) 1 u(A, S) Horvitz, 90
A Dynamics of Belief and Action eu(A, t) = p(S|E) u(A, S, t) + [1 - p(S|E)] u(A, S) eu(A) = p(S|E) u(A, S) + [1 - p(S|E)] u(A, S) 1. 0 u(A, S) 0. 8 Expected utility Action No 0 Eric Horvitz, April 5, 2003 p* p*’ 0. 6 u(A, S, t) Ac tio n p(S|E) u(A, S, t’ > t) 1 u(A, S) Horvitz, 90
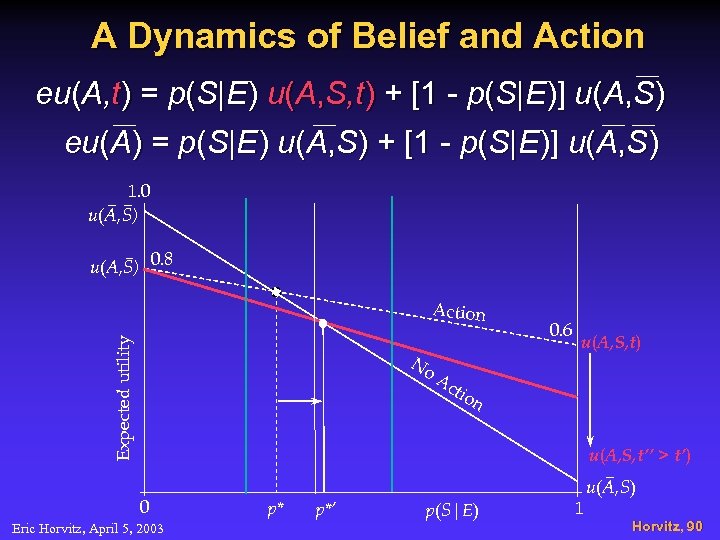 A Dynamics of Belief and Action eu(A, t) = p(S|E) u(A, S, t) + [1 - p(S|E)] u(A, S) eu(A) = p(S|E) u(A, S) + [1 - p(S|E)] u(A, S) 1. 0 u(A, S) 0. 8 Expected utility Action No 0. 6 u(A, S, t) Ac tio n u(A, S, t’’ > t’) 0 Eric Horvitz, April 5, 2003 p* p*’ p(S|E) 1 u(A, S) Horvitz, 90
A Dynamics of Belief and Action eu(A, t) = p(S|E) u(A, S, t) + [1 - p(S|E)] u(A, S) eu(A) = p(S|E) u(A, S) + [1 - p(S|E)] u(A, S) 1. 0 u(A, S) 0. 8 Expected utility Action No 0. 6 u(A, S, t) Ac tio n u(A, S, t’’ > t’) 0 Eric Horvitz, April 5, 2003 p* p*’ p(S|E) 1 u(A, S) Horvitz, 90
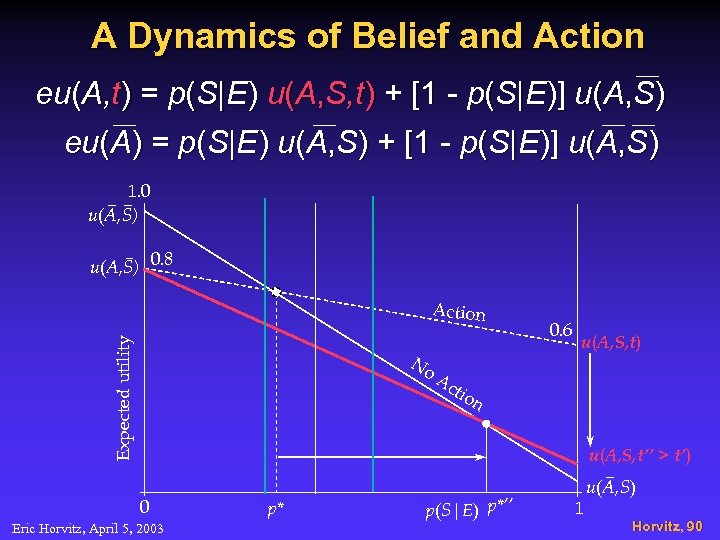 A Dynamics of Belief and Action eu(A, t) = p(S|E) u(A, S, t) + [1 - p(S|E)] u(A, S) eu(A) = p(S|E) u(A, S) + [1 - p(S|E)] u(A, S) 1. 0 u(A, S) 0. 8 Expected utility Action No 0. 6 u(A, S, t) Ac tio n u(A, S, t’’ > t’) 0 Eric Horvitz, April 5, 2003 p* p(S|E) p*’’ 1 u(A, S) Horvitz, 90
A Dynamics of Belief and Action eu(A, t) = p(S|E) u(A, S, t) + [1 - p(S|E)] u(A, S) eu(A) = p(S|E) u(A, S) + [1 - p(S|E)] u(A, S) 1. 0 u(A, S) 0. 8 Expected utility Action No 0. 6 u(A, S, t) Ac tio n u(A, S, t’’ > t’) 0 Eric Horvitz, April 5, 2003 p* p(S|E) p*’’ 1 u(A, S) Horvitz, 90
 Expected Value of Computation (EVC) n Understanding the influence of computational deliberation on expected value of ultimate action in world n Analog to expected value of information n Challenges: Eric Horvitz, April 5, 2003 Tractable approximations
Expected Value of Computation (EVC) n Understanding the influence of computational deliberation on expected value of ultimate action in world n Analog to expected value of information n Challenges: Eric Horvitz, April 5, 2003 Tractable approximations
![Expected Value of Computation p(I) p[ p’(I) ] t S 1 p[ p’(I) ] Expected Value of Computation p(I) p[ p’(I) ] t S 1 p[ p’(I) ]](https://present5.com/presentation/6b0ed62e045f6b42e633f40a0dbdfd61/image-59.jpg) Expected Value of Computation p(I) p[ p’(I) ] t S 1 p[ p’(I) ] p[ u’(I) ] p(I) p’(I) Eric Horvitz, April 5, 2003 Sn u’(I)
Expected Value of Computation p(I) p[ p’(I) ] t S 1 p[ p’(I) ] p[ u’(I) ] p(I) p’(I) Eric Horvitz, April 5, 2003 Sn u’(I)
 Expected Value of Computation (EVC) n Expected value of computation (EVC) analog to EVI Consider costs of delay and changes in quality of result with computation. Sum over uncertainty n n n Computation procedure C Problem instance I Partial result p(I) Computation time r EVC = å u( pi ( I ), to + r ) p( pi ( I )| C, I , r ) - u( I , to ) pi ( I ) Eric Horvitz, April 5, 2003 Horvitz, 90
Expected Value of Computation (EVC) n Expected value of computation (EVC) analog to EVI Consider costs of delay and changes in quality of result with computation. Sum over uncertainty n n n Computation procedure C Problem instance I Partial result p(I) Computation time r EVC = å u( pi ( I ), to + r ) p( pi ( I )| C, I , r ) - u( I , to ) pi ( I ) Eric Horvitz, April 5, 2003 Horvitz, 90
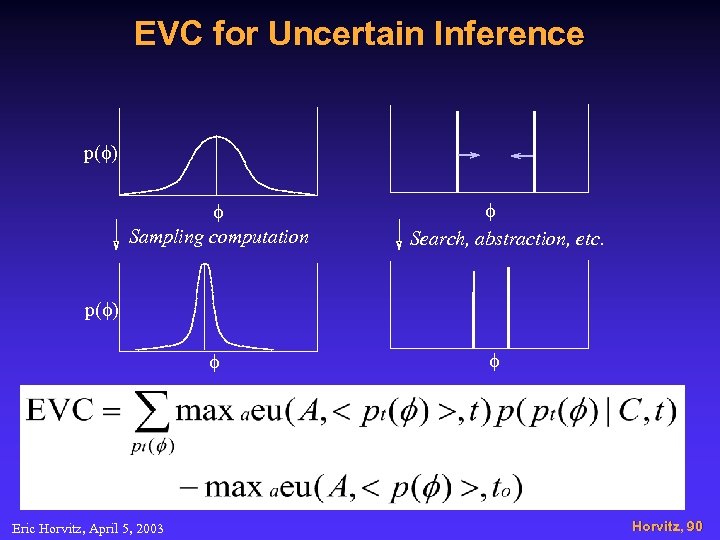 EVC for Uncertain Inference p(f) f Sampling computation f Search, abstraction, etc. p(f) f Eric Horvitz, April 5, 2003 f Horvitz, 90
EVC for Uncertain Inference p(f) f Sampling computation f Search, abstraction, etc. p(f) f Eric Horvitz, April 5, 2003 f Horvitz, 90
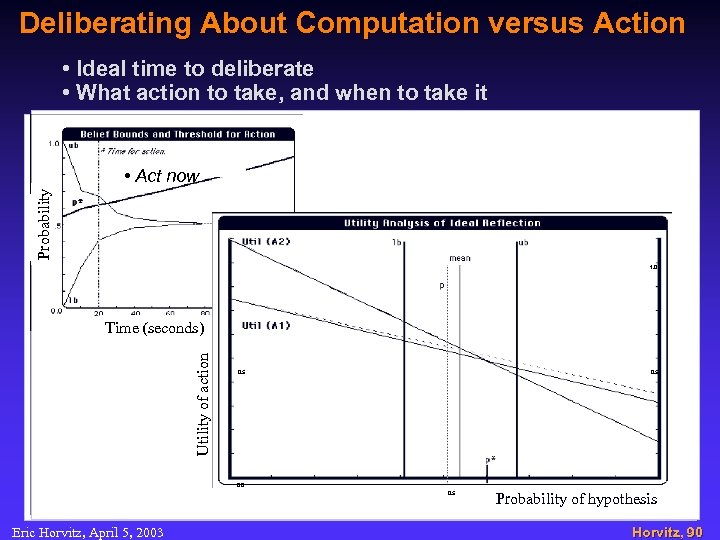 Deliberating About Computation versus Action • Ideal time to deliberate • What action to take, and when to take it Probability • Act now Utility of action Time (seconds) Utility 1. 0 0. 5 0. 0 0. 5 Eric Horvitz, April 5, 2003 Probabilityof H 1 H Probability of 1. 0 Probability of hypothesis 1 Horvitz, 90
Deliberating About Computation versus Action • Ideal time to deliberate • What action to take, and when to take it Probability • Act now Utility of action Time (seconds) Utility 1. 0 0. 5 0. 0 0. 5 Eric Horvitz, April 5, 2003 Probabilityof H 1 H Probability of 1. 0 Probability of hypothesis 1 Horvitz, 90
 Rich Dynamics of Belief and Action Eric Horvitz, April 5, 2003 Horvitz, 90
Rich Dynamics of Belief and Action Eric Horvitz, April 5, 2003 Horvitz, 90
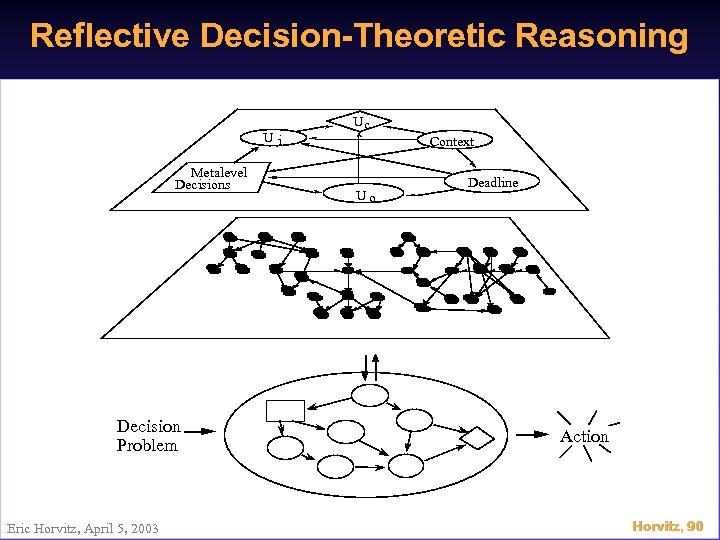 Reflective Decision-Theoretic Reasoning Ui Metalevel Decisions Decision Problem Eric Horvitz, April 5, 2003 Uc Context Uo Deadline Action Horvitz, 90
Reflective Decision-Theoretic Reasoning Ui Metalevel Decisions Decision Problem Eric Horvitz, April 5, 2003 Uc Context Uo Deadline Action Horvitz, 90
 Challenges of Type II Decision Models n Reasoning about extent of EVC analysis n Offline compilation, invoke multi-level real-time analyses? n Overall: Ideal partition of resources to different phases of reasoning Eric Horvitz, April 5, 2003
Challenges of Type II Decision Models n Reasoning about extent of EVC analysis n Offline compilation, invoke multi-level real-time analyses? n Overall: Ideal partition of resources to different phases of reasoning Eric Horvitz, April 5, 2003
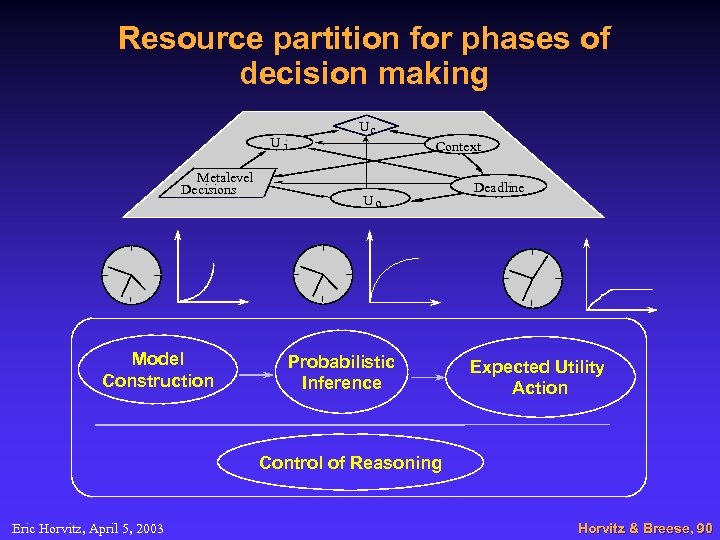 Resource partition for phases of decision making Ui Metalevel Decisions Model Construction Uc Context Uo Probabilistic Inference Deadline Expected Utility Action Control of Reasoning Eric Horvitz, April 5, 2003 Horvitz & Breese, 90
Resource partition for phases of decision making Ui Metalevel Decisions Model Construction Uc Context Uo Probabilistic Inference Deadline Expected Utility Action Control of Reasoning Eric Horvitz, April 5, 2003 Horvitz & Breese, 90
 Understanding & Automated Modeling Processes n Automated model construction n Understand situation, deliberate like a decision analyst about distinctions and relationships n Refinement of different dimensions of model Eric Horvitz, April 5, 2003
Understanding & Automated Modeling Processes n Automated model construction n Understand situation, deliberate like a decision analyst about distinctions and relationships n Refinement of different dimensions of model Eric Horvitz, April 5, 2003
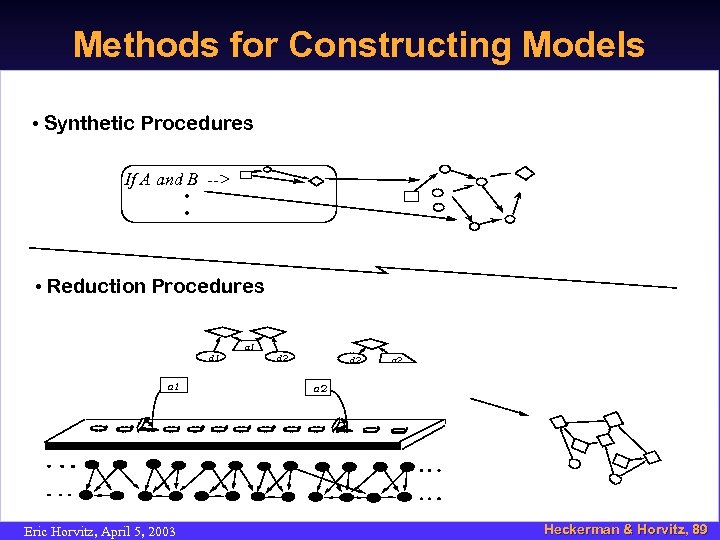 Methods for Constructing Models • Synthetic Procedures If A and B --> • • • Reduction Procedures a 1 d 1 a 1 Eric Horvitz, April 5, 2003 d 2 a 2 Heckerman & Horvitz, 89
Methods for Constructing Models • Synthetic Procedures If A and B --> • • • Reduction Procedures a 1 d 1 a 1 Eric Horvitz, April 5, 2003 d 2 a 2 Heckerman & Horvitz, 89
 Dynamic Construction of Pt-Specific Models Eric Horvitz, April 5, 2003
Dynamic Construction of Pt-Specific Models Eric Horvitz, April 5, 2003
 Dynamic Construction of Pt-Specific Models Eric Horvitz, April 5, 2003
Dynamic Construction of Pt-Specific Models Eric Horvitz, April 5, 2003
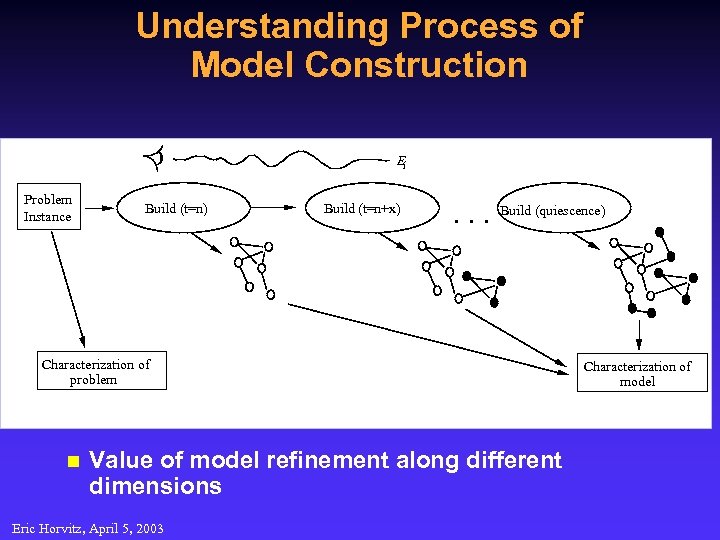 Understanding Process of Model Construction Ei Problem Instance Build (t=n) Build (t=n+x) • • • Build (quiescence) Characterization of problem n Value of model refinement along different dimensions Eric Horvitz, April 5, 2003 Characterization of model
Understanding Process of Model Construction Ei Problem Instance Build (t=n) Build (t=n+x) • • • Build (quiescence) Characterization of problem n Value of model refinement along different dimensions Eric Horvitz, April 5, 2003 Characterization of model
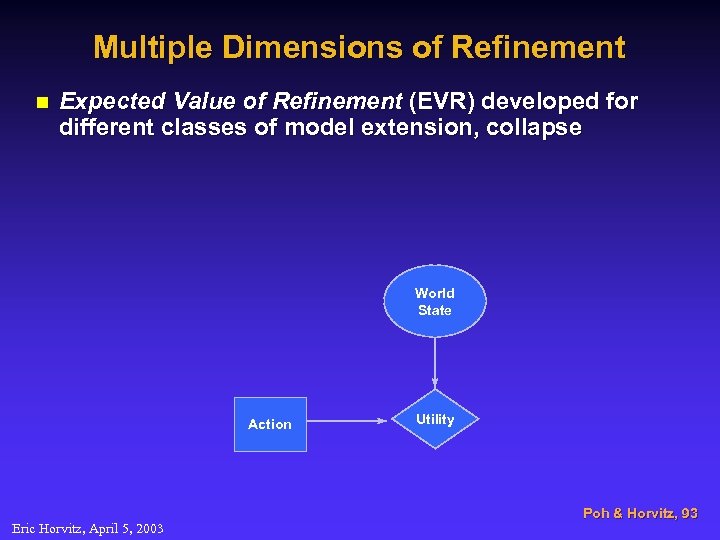 Multiple Dimensions of Refinement n Expected Value of Refinement (EVR) developed for different classes of model extension, collapse World State Action Eric Horvitz, April 5, 2003 Utility Poh & Horvitz, 93
Multiple Dimensions of Refinement n Expected Value of Refinement (EVR) developed for different classes of model extension, collapse World State Action Eric Horvitz, April 5, 2003 Utility Poh & Horvitz, 93
 Multiple Dimensions of Refinement n Conceptual refinement World State Action Eric Horvitz, April 5, 2003 Utility Poh & Horvitz, 93
Multiple Dimensions of Refinement n Conceptual refinement World State Action Eric Horvitz, April 5, 2003 Utility Poh & Horvitz, 93
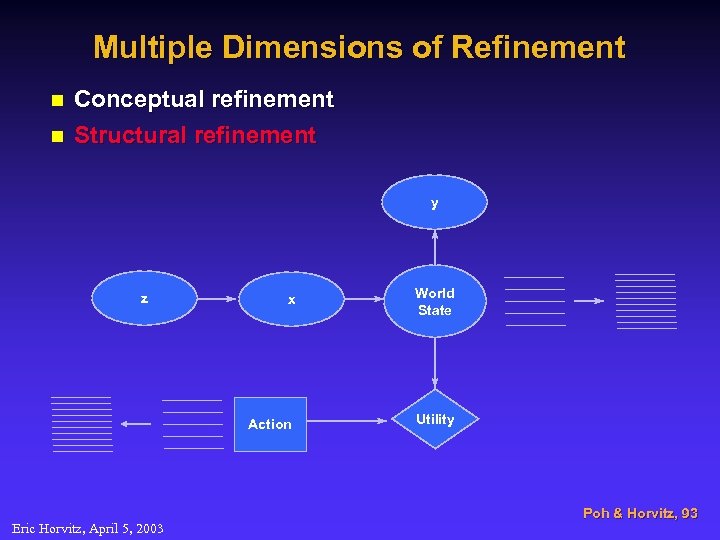 Multiple Dimensions of Refinement n n Conceptual refinement Structural refinement y Eric Horvitz, April 5, 2003 x World State Action z Utility Poh & Horvitz, 93
Multiple Dimensions of Refinement n n Conceptual refinement Structural refinement y Eric Horvitz, April 5, 2003 x World State Action z Utility Poh & Horvitz, 93
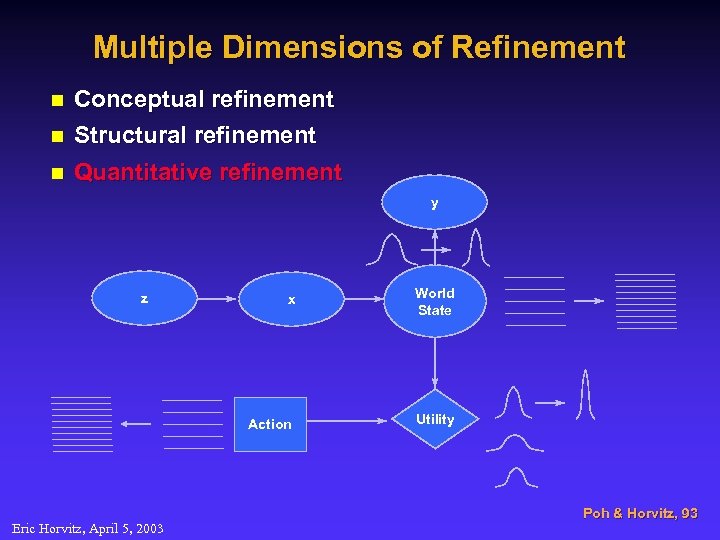 Multiple Dimensions of Refinement n Conceptual refinement Structural refinement n Quantitative refinement n y Eric Horvitz, April 5, 2003 x World State Action z Utility Poh & Horvitz, 93
Multiple Dimensions of Refinement n Conceptual refinement Structural refinement n Quantitative refinement n y Eric Horvitz, April 5, 2003 x World State Action z Utility Poh & Horvitz, 93
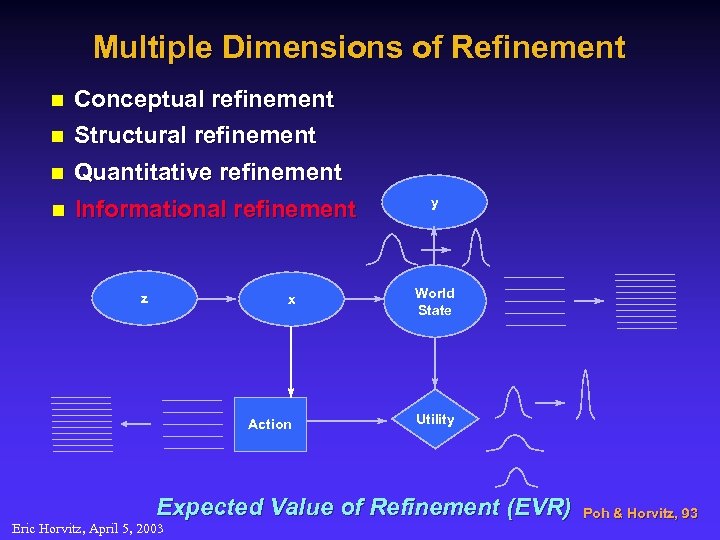 Multiple Dimensions of Refinement n Conceptual refinement Structural refinement n Quantitative refinement n Informational refinement n y x World State Action z Utility Expected Value of Refinement (EVR) Eric Horvitz, April 5, 2003 Poh & Horvitz, 93
Multiple Dimensions of Refinement n Conceptual refinement Structural refinement n Quantitative refinement n Informational refinement n y x World State Action z Utility Expected Value of Refinement (EVR) Eric Horvitz, April 5, 2003 Poh & Horvitz, 93
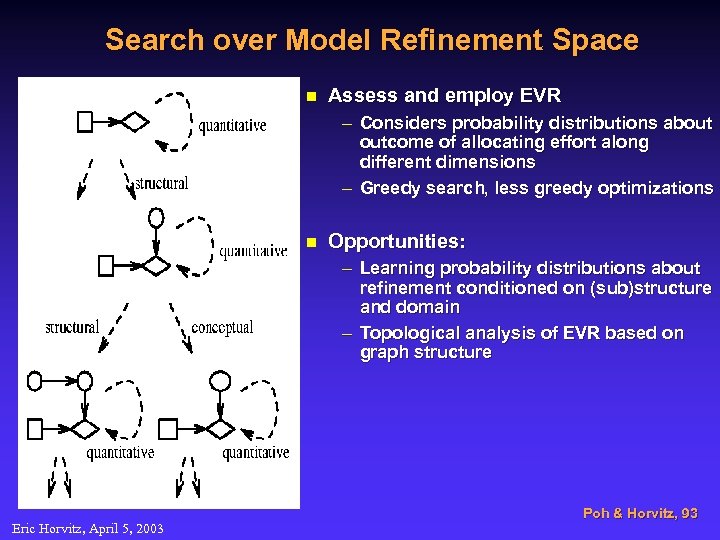 Search over Model Refinement Space n Assess and employ EVR – Considers probability distributions about outcome of allocating effort along different dimensions – Greedy search, less greedy optimizations n Opportunities: – Learning probability distributions about refinement conditioned on (sub)structure and domain – Topological analysis of EVR based on graph structure Eric Horvitz, April 5, 2003 Poh & Horvitz, 93
Search over Model Refinement Space n Assess and employ EVR – Considers probability distributions about outcome of allocating effort along different dimensions – Greedy search, less greedy optimizations n Opportunities: – Learning probability distributions about refinement conditioned on (sub)structure and domain – Topological analysis of EVR based on graph structure Eric Horvitz, April 5, 2003 Poh & Horvitz, 93
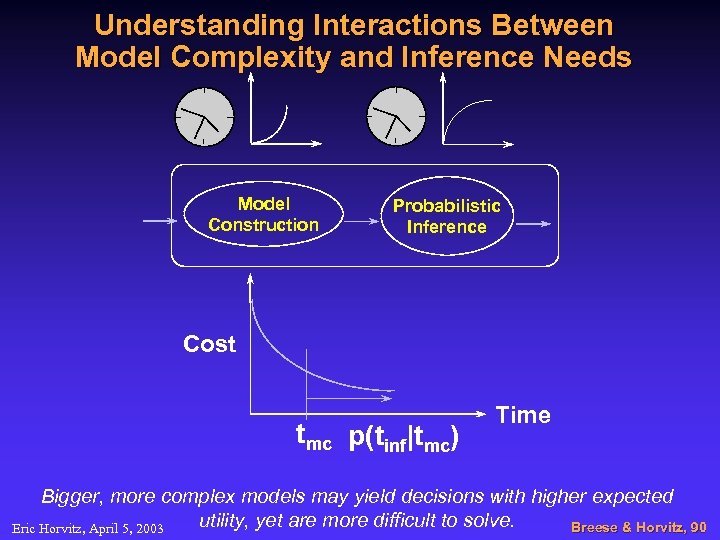 Understanding Interactions Between Model Complexity and Inference Needs Model Construction Probabilistic Inference Cost tmc p(tinf|tmc) Time Bigger, more complex models may yield decisions with higher expected utility, yet are more difficult to solve. Breese & Horvitz, 90 Eric Horvitz, April 5, 2003
Understanding Interactions Between Model Complexity and Inference Needs Model Construction Probabilistic Inference Cost tmc p(tinf|tmc) Time Bigger, more complex models may yield decisions with higher expected utility, yet are more difficult to solve. Breese & Horvitz, 90 Eric Horvitz, April 5, 2003
 Challenges n Rational decision making under resource constraints—generalizations beyond special cases n Harnessing EVI, EVR, EVC in parallel to guide decision making n Autonomous decision systems immersed in an environment Eric Horvitz, April 5, 2003
Challenges n Rational decision making under resource constraints—generalizations beyond special cases n Harnessing EVI, EVR, EVC in parallel to guide decision making n Autonomous decision systems immersed in an environment Eric Horvitz, April 5, 2003
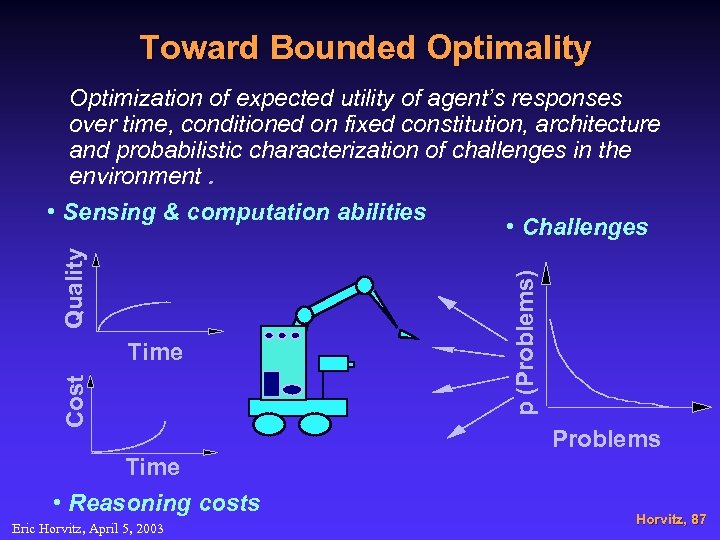 Toward Bounded Optimality Cost Time • Reasoning costs Eric Horvitz, April 5, 2003 p (Problems) Quality Optimization of expected utility of agent’s responses over time, conditioned on fixed constitution, architecture and probabilistic characterization of challenges in the environment. • Sensing & computation abilities • Challenges Problems Horvitz, 87
Toward Bounded Optimality Cost Time • Reasoning costs Eric Horvitz, April 5, 2003 p (Problems) Quality Optimization of expected utility of agent’s responses over time, conditioned on fixed constitution, architecture and probabilistic characterization of challenges in the environment. • Sensing & computation abilities • Challenges Problems Horvitz, 87
 Allocation of Resources to Streams of Decision Problems Over Time In pursuit of ideal strategies for harnessing all available time for solving sequences of challenges. n Environments typified by single challenges, bursts of challenges interspersed with idle time. n Seek ideal approach to best leverage idle time. n Applications to problem solving, communication under varying, limited resources Eric Horvitz, April 5, 2003
Allocation of Resources to Streams of Decision Problems Over Time In pursuit of ideal strategies for harnessing all available time for solving sequences of challenges. n Environments typified by single challenges, bursts of challenges interspersed with idle time. n Seek ideal approach to best leverage idle time. n Applications to problem solving, communication under varying, limited resources Eric Horvitz, April 5, 2003
 Stream of Problem Instances Time Eric Horvitz, April 5, 2003 Horvitz, 96
Stream of Problem Instances Time Eric Horvitz, April 5, 2003 Horvitz, 96
 Stream of Problem Instances Time Eric Horvitz, April 5, 2003 Horvitz, 96
Stream of Problem Instances Time Eric Horvitz, April 5, 2003 Horvitz, 96
 Stream of Problem Instances Time Eric Horvitz, April 5, 2003 Horvitz, 96
Stream of Problem Instances Time Eric Horvitz, April 5, 2003 Horvitz, 96
 Stream of Problem Instances Time Eric Horvitz, April 5, 2003 Horvitz, 96
Stream of Problem Instances Time Eric Horvitz, April 5, 2003 Horvitz, 96
 Personal Computing Eric Horvitz, April 5, 2003
Personal Computing Eric Horvitz, April 5, 2003
 Time Eric Horvitz, April 5, 2003 Horvitz, 96
Time Eric Horvitz, April 5, 2003 Horvitz, 96
 Time Eric Horvitz, April 5, 2003 Horvitz, 96
Time Eric Horvitz, April 5, 2003 Horvitz, 96
 Time Eric Horvitz, April 5, 2003 Horvitz, 96
Time Eric Horvitz, April 5, 2003 Horvitz, 96
 Time Eric Horvitz, April 5, 2003 Horvitz, 96
Time Eric Horvitz, April 5, 2003 Horvitz, 96
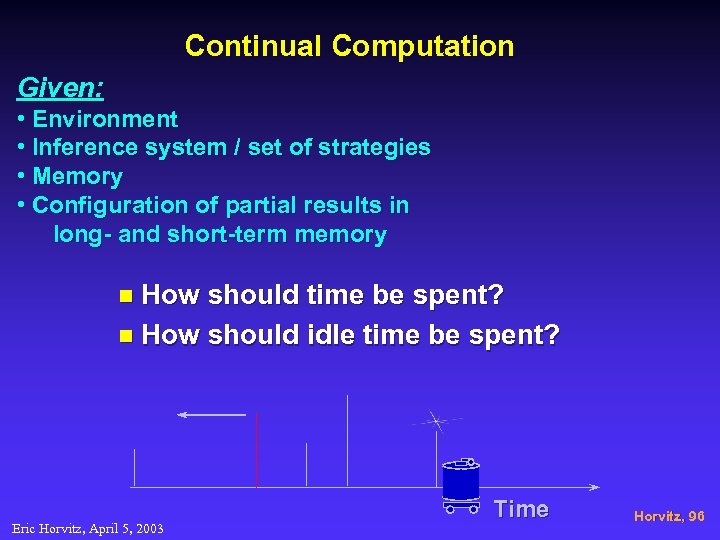 Continual Computation Given: • Environment • Inference system / set of strategies • Memory • Configuration of partial results in long- and short-term memory n How should time be spent? n How should idle time be spent? Eric Horvitz, April 5, 2003 Time Horvitz, 96
Continual Computation Given: • Environment • Inference system / set of strategies • Memory • Configuration of partial results in long- and short-term memory n How should time be spent? n How should idle time be spent? Eric Horvitz, April 5, 2003 Time Horvitz, 96
 Models of Continual Computation • Different models based on distinct sets of assumptions • Seek approximate, tractable analyses based on reasonable assumptions • Results for all-or-nothing as well as for flexible strategies yielding partial results Minimize future delays Maximize expected value Eric Horvitz, April 5, 2003 Horvitz, 96
Models of Continual Computation • Different models based on distinct sets of assumptions • Seek approximate, tractable analyses based on reasonable assumptions • Results for all-or-nothing as well as for flexible strategies yielding partial results Minimize future delays Maximize expected value Eric Horvitz, April 5, 2003 Horvitz, 96
 Models of Continual Computation Consider: • Probability distribution over idle-time, p( T | E ) • Probability distribution over future problems, p( Ii | E ) Eric Horvitz, April 5, 2003 Horvitz, 96
Models of Continual Computation Consider: • Probability distribution over idle-time, p( T | E ) • Probability distribution over future problems, p( Ii | E ) Eric Horvitz, April 5, 2003 Horvitz, 96
 Expected Value of Precomputation n Add consideration of uncertainty in future problem instances Eric Horvitz, April 5, 2003 Horvitz, 96
Expected Value of Precomputation n Add consideration of uncertainty in future problem instances Eric Horvitz, April 5, 2003 Horvitz, 96
 EVP Flux of a Precomputation Strategy n EVP Flux: Instantaneous rate at which EVP increases with precomputation Eric Horvitz, April 5, 2003 Horvitz, 96
EVP Flux of a Precomputation Strategy n EVP Flux: Instantaneous rate at which EVP increases with precomputation Eric Horvitz, April 5, 2003 Horvitz, 96
 Minimizing Computational Delay • Assume all-or-nothing problems • Goal: Minimize expected delay for reaching complete solutions to challenges posed in the next period(s) • Theorem: Idle-Time Partition The optimal policy is to spend available idle time solving future problems completely, in order of their probability. p( I 1 | E ) p( I 2 | E ) p( I n | E ) > p( I n+1 | E ) Eric Horvitz, April 5, 2003 p( I 3 | E ) p( In | E )
Minimizing Computational Delay • Assume all-or-nothing problems • Goal: Minimize expected delay for reaching complete solutions to challenges posed in the next period(s) • Theorem: Idle-Time Partition The optimal policy is to spend available idle time solving future problems completely, in order of their probability. p( I 1 | E ) p( I 2 | E ) p( I n | E ) > p( I n+1 | E ) Eric Horvitz, April 5, 2003 p( I 3 | E ) p( In | E )
 Considering Value of Partial Results • Consider value of partial results, p(I) • Maximize expected value of a system’s response p( I 1 | E ) p( I 2 | E ) p( I 3 | E ) p( In | E ) Eric Horvitz, April 5, 2003 Horvitz, 01
Considering Value of Partial Results • Consider value of partial results, p(I) • Maximize expected value of a system’s response p( I 1 | E ) p( I 2 | E ) p( I 3 | E ) p( In | E ) Eric Horvitz, April 5, 2003 Horvitz, 01
 Policy for Concave Profiles First derivative of utility positive with computation, second derivative is nonpositive. • Theorem: Ideal policy: continue to allocate resources to solving the problem with the highest instantaneous expected value flux. n I 1 p 1 Transformation to expectation p 2 I 2 EVP p 3 I 3 Eric Horvitz, April 5, 2003 I 2 I 1 I 3 Horvitz, 01
Policy for Concave Profiles First derivative of utility positive with computation, second derivative is nonpositive. • Theorem: Ideal policy: continue to allocate resources to solving the problem with the highest instantaneous expected value flux. n I 1 p 1 Transformation to expectation p 2 I 2 EVP p 3 I 3 Eric Horvitz, April 5, 2003 I 2 I 1 I 3 Horvitz, 01
 Beyond Idle Time: Trading Off Present for Future • It can be worth slowing down solution of current problems for enhancing solution of future problems • Time preference captured: Value of results available in future period discounted with time • Solution for case of problem solving in next period Eric Horvitz, April 5, 2003 Horvitz, 99
Beyond Idle Time: Trading Off Present for Future • It can be worth slowing down solution of current problems for enhancing solution of future problems • Time preference captured: Value of results available in future period discounted with time • Solution for case of problem solving in next period Eric Horvitz, April 5, 2003 Horvitz, 99
 Trading Off Present for Future Time Eric Horvitz, April 5, 2003 Horvitz, 99
Trading Off Present for Future Time Eric Horvitz, April 5, 2003 Horvitz, 99
 Trading Off Present for Future Time Eric Horvitz, April 5, 2003 Horvitz, 99
Trading Off Present for Future Time Eric Horvitz, April 5, 2003 Horvitz, 99
 Trading Off Present for Future Time Eric Horvitz, April 5, 2003 Horvitz, 99
Trading Off Present for Future Time Eric Horvitz, April 5, 2003 Horvitz, 99
 Trading Off Present for Future Time Eric Horvitz, April 5, 2003 Horvitz, 99
Trading Off Present for Future Time Eric Horvitz, April 5, 2003 Horvitz, 99
 Trading Off Present for Future Time Eric Horvitz, April 5, 2003 Horvitz, 99
Trading Off Present for Future Time Eric Horvitz, April 5, 2003 Horvitz, 99
 Trading Off Present for Future Time Eric Horvitz, April 5, 2003 Horvitz, 99
Trading Off Present for Future Time Eric Horvitz, April 5, 2003 Horvitz, 99
 Trading Off Present for Future Time Eric Horvitz, April 5, 2003 Horvitz, 99
Trading Off Present for Future Time Eric Horvitz, April 5, 2003 Horvitz, 99
 Redirecting Resources from Present to Future Problems Value of redirection depends on: • Probability distribution over future idle time • Sensitivity of flux of pending EVP policy to changes in amount of idle time • Net EVC of ongoing computation • Time preference on behavior Eric Horvitz, April 5, 2003 Horvitz, 99
Redirecting Resources from Present to Future Problems Value of redirection depends on: • Probability distribution over future idle time • Sensitivity of flux of pending EVP policy to changes in amount of idle time • Net EVC of ongoing computation • Time preference on behavior Eric Horvitz, April 5, 2003 Horvitz, 99
 Continual Computation: Applications • Diverse computational applications: Networking, operating system, software applications • Diagnosis Eric Horvitz, April 5, 2003 Horvitz, 99
Continual Computation: Applications • Diverse computational applications: Networking, operating system, software applications • Diagnosis Eric Horvitz, April 5, 2003 Horvitz, 99
 Example: Value of Information in Decision-Theoretic Diagnostic Systems • Sequential diagnostic reasoning systems • Probability distributions over entities of interest • Expected value of evaluating new observations • Typical to have idle time between recommendations • Harness continual computation to precompute probability distributions and recommendations Eric Horvitz, April 5, 2003 Horvitz, 99
Example: Value of Information in Decision-Theoretic Diagnostic Systems • Sequential diagnostic reasoning systems • Probability distributions over entities of interest • Expected value of evaluating new observations • Typical to have idle time between recommendations • Harness continual computation to precompute probability distributions and recommendations Eric Horvitz, April 5, 2003 Horvitz, 99
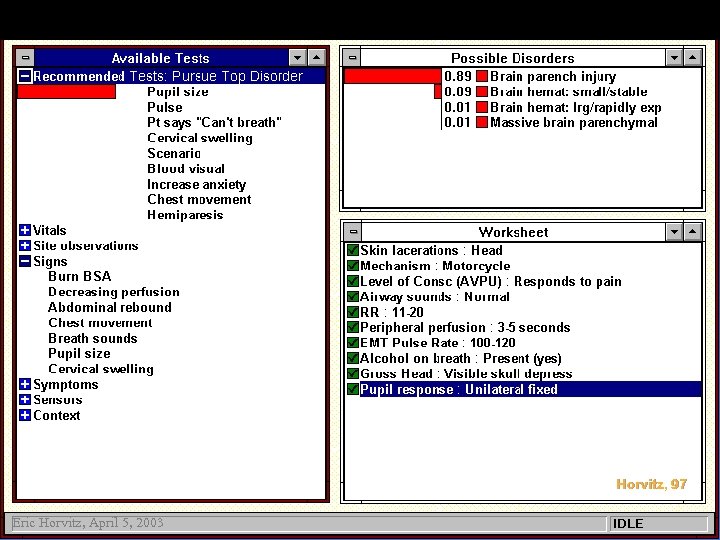
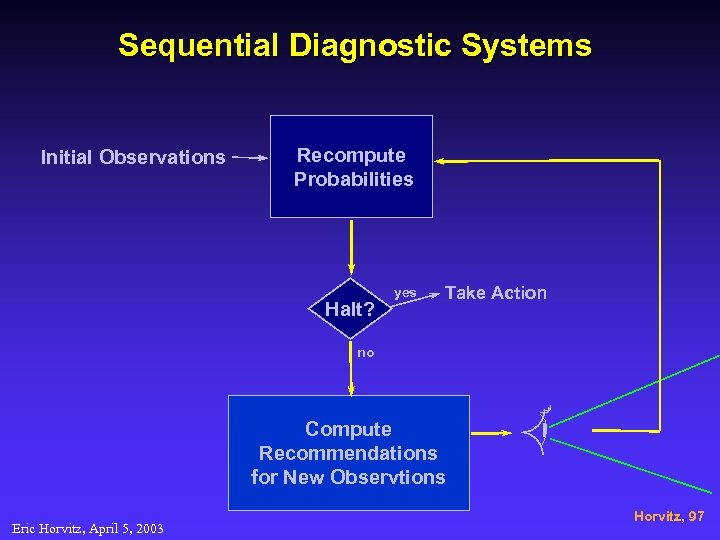 Sequential Diagnostic Systems Initial Observations Recompute Probabilities Halt? yes Take Action no Compute Recommendations for New Observtions Eric Horvitz, April 5, 2003 Horvitz, 97
Sequential Diagnostic Systems Initial Observations Recompute Probabilities Halt? yes Take Action no Compute Recommendations for New Observtions Eric Horvitz, April 5, 2003 Horvitz, 97
 Horvitz, 97 Eric Horvitz, April 5, 2003 Eric Horvitz, February 2003 UW Lecture
Horvitz, 97 Eric Horvitz, April 5, 2003 Eric Horvitz, February 2003 UW Lecture
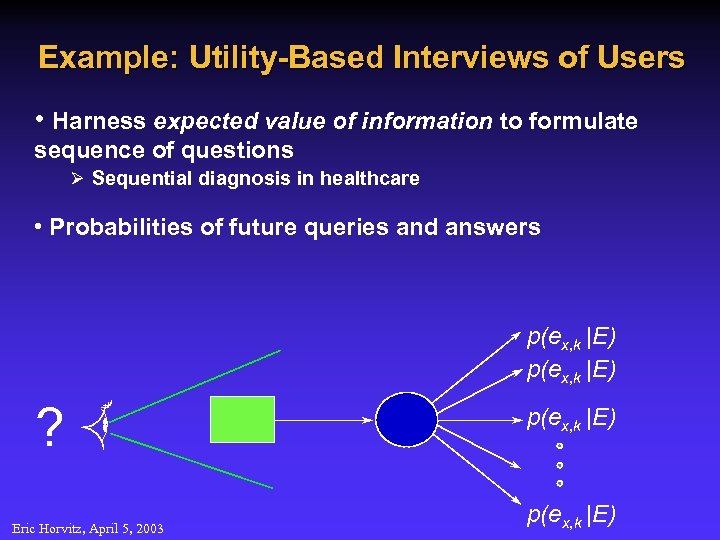 Example: Utility-Based Interviews of Users • Harness expected value of information to formulate sequence of questions Ø Sequential diagnosis in healthcare • Probabilities of future queries and answers p(ex, k |E) ? Eric Horvitz, April 5, 2003 p(ex, k |E)
Example: Utility-Based Interviews of Users • Harness expected value of information to formulate sequence of questions Ø Sequential diagnosis in healthcare • Probabilities of future queries and answers p(ex, k |E) ? Eric Horvitz, April 5, 2003 p(ex, k |E)
 Computing Value of Information • Consider best actions after observations, conditioned on current information. - Tests, ex - Observations, ex, k Eric Horvitz, April 5, 2003 Horvitz, 96
Computing Value of Information • Consider best actions after observations, conditioned on current information. - Tests, ex - Observations, ex, k Eric Horvitz, April 5, 2003 Horvitz, 96
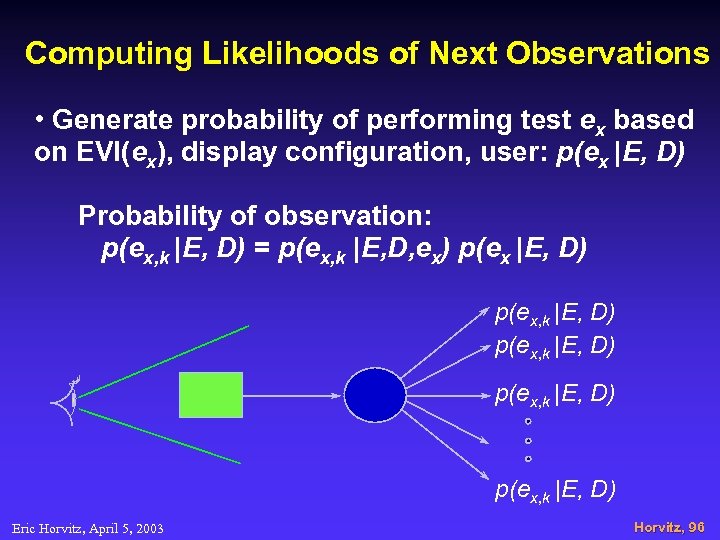 Computing Likelihoods of Next Observations • Generate probability of performing test ex based on EVI(ex), display configuration, user: p(ex |E, D) Probability of observation: p(ex, k |E, D) = p(ex, k |E, D, ex) p(ex |E, D) p(ex, k |E, D) Eric Horvitz, April 5, 2003 Horvitz, 96
Computing Likelihoods of Next Observations • Generate probability of performing test ex based on EVI(ex), display configuration, user: p(ex |E, D) Probability of observation: p(ex, k |E, D) = p(ex, k |E, D, ex) p(ex |E, D) p(ex, k |E, D) Eric Horvitz, April 5, 2003 Horvitz, 96
 Continual Computation for Prefetching Web Pages How should networking resources be expended? n Utility models for partial documents n Policies that maximize expected utility Time Eric Horvitz, April 5, 2003 Horvitz, 98
Continual Computation for Prefetching Web Pages How should networking resources be expended? n Utility models for partial documents n Policies that maximize expected utility Time Eric Horvitz, April 5, 2003 Horvitz, 98
 Statistical Models of Access from Server Log Data • Markov assumption • Training data: 95, 000 transitions p(next url | current url) • Test data: 6, 000 transitions URL to Eric Horvitz, April 5, 2003 URL t+1 Horvitz, 98
Statistical Models of Access from Server Log Data • Markov assumption • Training data: 95, 000 transitions p(next url | current url) • Test data: 6, 000 transitions URL to Eric Horvitz, April 5, 2003 URL t+1 Horvitz, 98
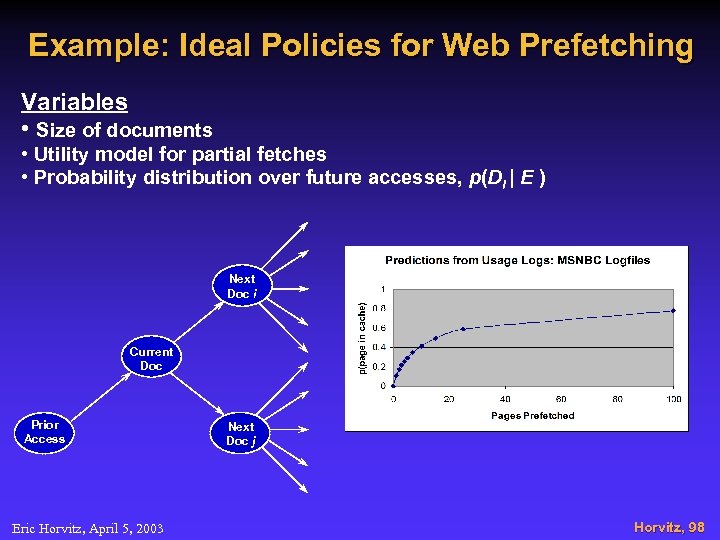 Example: Ideal Policies for Web Prefetching Variables • Size of documents • Utility model for partial fetches • Probability distribution over future accesses, p(Di | E ) Next Doc i Current Doc Prior Access Eric Horvitz, April 5, 2003 Next Doc j Horvitz, 98
Example: Ideal Policies for Web Prefetching Variables • Size of documents • Utility model for partial fetches • Probability distribution over future accesses, p(Di | E ) Next Doc i Current Doc Prior Access Eric Horvitz, April 5, 2003 Next Doc j Horvitz, 98
 Directions Modeling & inference under bounded resources n Characterizing incompleteness; understanding influence of model refinements, approximation on MEU of inferred A* n Ideal allocation of resources to distinct dimensions of modeling refinement and reasoning, given cost of resources n Embedded autonomous decision systems Toward principles of action under limited resources Eric Horvitz, April 5, 2003
Directions Modeling & inference under bounded resources n Characterizing incompleteness; understanding influence of model refinements, approximation on MEU of inferred A* n Ideal allocation of resources to distinct dimensions of modeling refinement and reasoning, given cost of resources n Embedded autonomous decision systems Toward principles of action under limited resources Eric Horvitz, April 5, 2003


