Decision Trees Decision tree induction is

Decision Trees

Decision tree induction is the learning of decision trees from class -labelled training examples. A decision-treeis a flow-chart like tree structure, where each internal node denotes a test on an attribute, each branch represents an outcome of the test and each leaf node holds a class label.

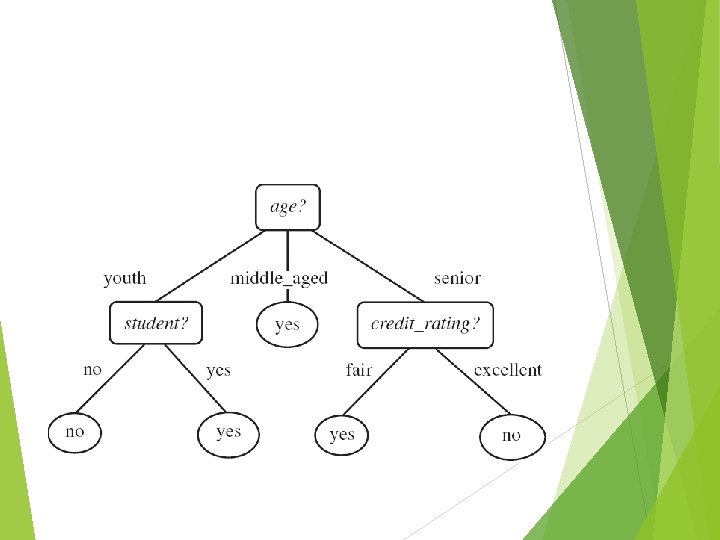
Decision Tree Induction ID 3 Iterative Dichotomiser by J. Ross 3 Quinlan C 4. 5 is a successor of ID 3 Classification and Regression Trees(CART) – generation of binary trees

ID 3, C 4. 5 and CART adopt a greedy(nonbacktracking) approach in which decision trees are constructed in a top-down recursive divide-and-conquer manner. Algorithm starts with a training set of tuples and their associated class labels. Training stet is recursively partitioned into smaller subsets as the tree is being built.

The Algorithm Create a root node N for the tree If all examples are of same class C, then return N as the leaf node labeled with the class C. If attribute_list is empty, then return N as the leaf node labeled with the majority class in D(majority voting)

Apply Attribute_Selection_method (D, attribute_list) to find “best” splitting_criteria; Label node N with splitting_criterion If splitting_attribute is discrete_valued and multiway splits allowed then attribute_list – splitting_attribute

For each outcome j of splitting_criterion Let Dj be the set of data tuples in D satisfying outcome j; If Dj is empty then Attach a leaf labelled with the majority class in D to node N; Attach the node Generate_decision_tree(Dj, node N else Endfor Return N returned attribute_list) by to

To partition attributes in D, there are three possible scenarios. Let A be the splitting attribute. A has v distinct values, {a 1, a 2, …, av}, based on training data. A is discrete-valued: A is continuous-valued: A is discrete-valued and a binary tree must be produced.

The recursive partitioning stops only when one of the following terminating condition is true: There are no remaining attributes on which the tuples may be further partitioned. In this case majority voting is employed. All the tuples in partition D belong to the same class There are no tuples for a given branch, that is, a partition Dj, is empty. In this case, a leaf is created with the majority class in D. What is the computational complexity?

Attribute Selection Procedure It is a heuristic for selecting the splitting criterion that “best” separates a given data partition, D, of class-labelled training tuples into individual classes. It is also known as splitting rules because they determine how the tuples at a given node are to be split. It provides ranking for each attribute describing the given training tuple. The attribute having the best score for the measure is chosen as the splitting attribute for the given tuples. Well known attribute selection measures are : information gain, gain ratio, gini index.

Information Gain(ID 3/C 4. 5) Select the attribute with the highest information gain. Let pi be the probability that an arbitrary tuple in D belongs to class Ci, estimated by |Ci, D|/|D| Expected information (entropy) needed to classify a tuple in D:

Information needed (after using A to split D into v partitions) to classify D: Information gained by branching on attribute A

Exercise Calculate the information(entropy) Given: Set S contains 14 examples 9 Positive values 5 Negative values

Exercise Info(S) = - (9/14) log 2 (9/14) - (5/14) log 2 (5/14) = 0. 940

Information Gain Information gain is based on the decrease in entropy after a dataset is split on an attribute. Looking for which attribute creates the most homogeneous branches

Information Gain Example 14 examples, 9 positive 5 negative The attribute is Wind. Values of wind are Weak and Strong

Exercise (cont. ) 8 occurrences of weak winds 6 occurrences of strong winds For the weak winds, 6 are positive and 2 are negative For the strong winds, 3 are positive and 3 are negative

Exercise (cont. ) Gain(S, Wind) = Info(S) - (8/14) * Info(Weak) -(6/14) * Info(Strong) Info(Weak) = - (6/8)*log 2(6/8) - (2/8)*log 2(2/8) = 0. 811 Info(Strong) = - (3/6)*log 2(3/6) = 1. 00

Exercise (cont. ) So… 0. 940 - (8/14)*0. 811 - (6/14)*1. 00 = 0. 048

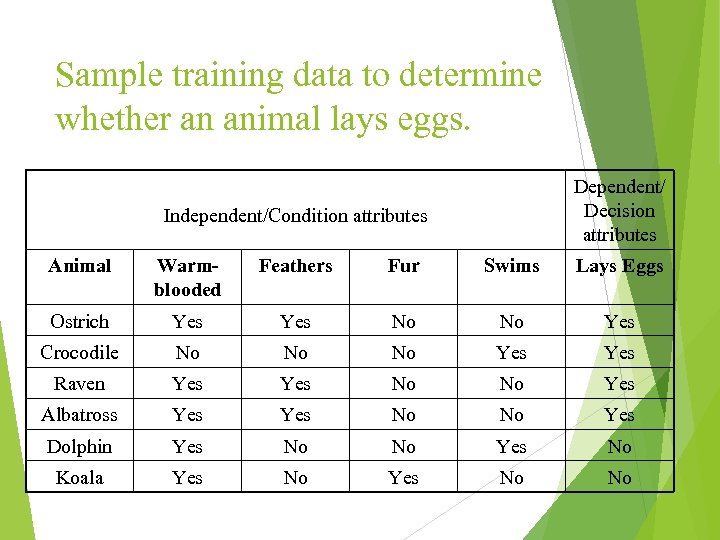Sample training data to determine whether an animal lays eggs. Dependent/ Decision attributes Independent/Condition attributes Animal Warmblooded Feathers Fur Swims Lays Eggs Ostrich Yes No No Yes Crocodile No No No Yes Raven Yes No No Yes Albatross Yes No No Yes Dolphin Yes No No Yes No Koala Yes No No

Entropy(4 Y, 2 N): -(4/6)log 2(4/6) – (2/6)log 2(2/6) = 0. 91829 Now, we have to find the IG for all four attributes Warm-blooded, Feathers, Fur, Swims

For attribute ‘Warm-blooded’: Values(Warm-blooded) : [Yes, No] S = [4 Y, 2 N] SYes = [3 Y, 2 N] E(SYes) = 0. 97095 SNo = [1 Y, 0 N] E(SNo) = 0 (all members belong to same class) Gain(S, Warm-blooded) = 0. 91829 – [(5/6)*0. 97095 + (1/6)*0] = 0. 10916 For attribute ‘Feathers’: Values(Feathers) : [Yes, No] S = [4 Y, 2 N] SYes = [3 Y, 0 N] E(SYes) = 0 SNo = [1 Y, 2 N] E(SNo) = 0. 91829 Gain(S, Feathers) = 0. 91829 – [(3/6)*0 + (3/6)*0. 91829] = 0. 45914

For attribute ‘Fur’: Values(Fur) : [Yes, No] S = [4 Y, 2 N] SYes = [0 Y, 1 N] E(SYes) = 0 SNo = [4 Y, 1 N] E(SNo) = 0. 7219 Gain(S, Fur) = 0. 91829 – [(1/6)*0 + (5/6)*0. 7219] = 0. 3167 For attribute ‘Swims’: Values(Swims) : [Yes, No] S = [4 Y, 2 N] SYes = [1 Y, 1 N] E(SYes) = 1 (equal members in both classes) SNo = [3 Y, 1 N] E(SNo) = 0. 81127

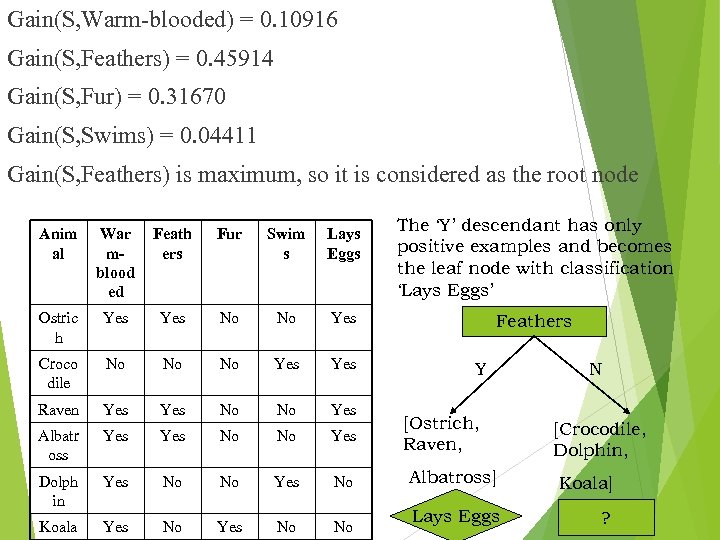Gain(S, Warm-blooded) = 0. 10916 Gain(S, Feathers) = 0. 45914 Gain(S, Fur) = 0. 31670 Gain(S, Swims) = 0. 04411 Gain(S, Feathers) is maximum, so it is considered as the root node Anim al War mblood ed Feath ers Fur Swim s Lays Eggs Ostric h Yes No No Yes Croco dile No No No Yes Raven Yes No No Yes Albatr oss Yes No No Yes Dolph in Yes No No Yes No Koala Yes No No The ‘Y’ descendant has only positive examples and becomes the leaf node with classification ‘Lays Eggs’ Feathers Y [Ostrich, Raven, N [Crocodile, Dolphin, Albatross] Koala] Lays Eggs ?

Animal Warmblooded Feathers Fur Swims Lays Eggs Crocodile No No No Yes Dolphin Yes No No Yes No Koala Yes No No We now repeat the procedure, S: [Crocodile, Dolphin, Koala] S: [1+, 2 -] Entropy(S) = -(1/3)log 2(1/3) – (2/3)log 2(2/3) = 0. 91829

For attribute ‘Warm-blooded’: Values(Warm-blooded) : [Yes, No] S = [1 Y, 2 N] SYes = [0 Y, 2 N] E(SYes) = 0 SNo = [1 Y, 0 N] E(SNo) = 0 Gain(S, Warm-blooded) = 0. 91829 – [(2/3)*0 + (1/3)*0] = 0. 91829 For attribute ‘Fur’: Values(Fur) : [Yes, No] S = [1 Y, 2 N] SYes = [0 Y, 1 N] E(SYes) = 0 SNo = [1 Y, 1 N] E(SNo) = 1 Gain(S, Fur) = 0. 91829 – [(1/3)*0 + (2/3)*1] = 0. 25162 For attribute ‘Swims’: Values(Swims) : [Yes, No] S = [1 Y, 2 N] SYes = [1 Y, 1 N] E(SYes) = 1 SNo = [0 Y, 1 N] E(SNo) = 0 Gain(S, Swims) = 0. 91829 – [(2/3)*1 + (1/3)*0] = 0. 25162 Gain(S, Warm-blooded) is maximum

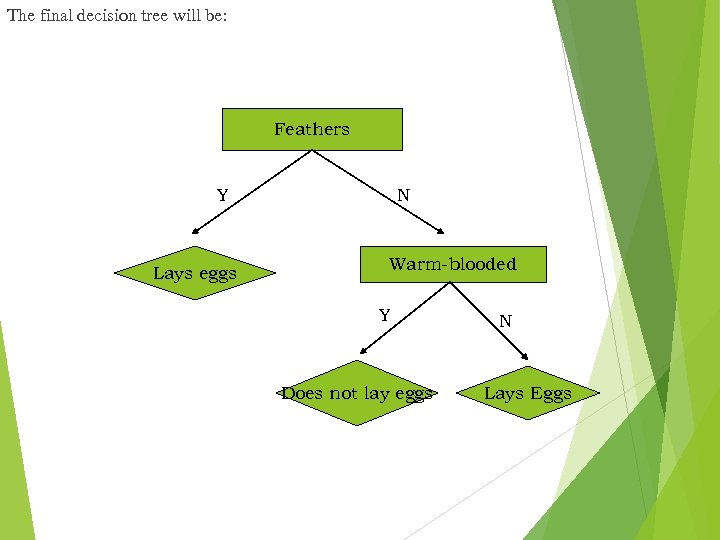The final decision tree will be: Feathers Y Lays eggs N Warm-blooded Y Does not lay eggs N Lays Eggs

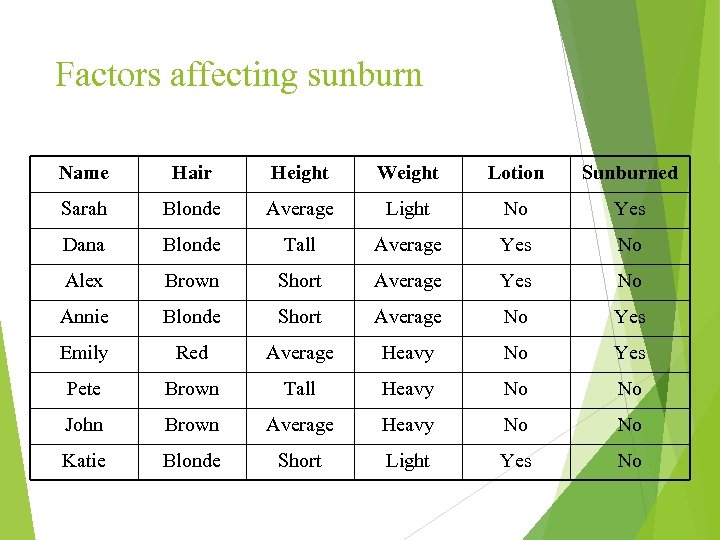Factors affecting sunburn Name Hair Height Weight Lotion Sunburned Sarah Blonde Average Light No Yes Dana Blonde Tall Average Yes No Alex Brown Short Average Yes No Annie Blonde Short Average No Yes Emily Red Average Heavy No Yes Pete Brown Tall Heavy No No John Brown Average Heavy No No Katie Blonde Short Light Yes No

S = [3+, 5 -] Entropy(S) = -(3/8)log 2(3/8) – (5/8)log 2(5/8) = 0. 95443 Find IG for all 4 attributes: Hair, Height, Weight, Lotion For attribute ‘Hair’: Values(Hair) : [Blonde, Brown, Red] S = [3+, 5 -] SBlonde = [2+, 2 -] E(SBlonde) = 1 SBrown = [0+, 3 -] E(SBrown) = 0 SRed = [1+, 0 -] E(SRed) = 0 Gain(S, Hair) = 0. 95443 – [(4/8)*1 + (3/8)*0 + (1/8)*0] = 0. 45443

For attribute ‘Height’: Values(Height) : [Average, Tall, Short] SAverage = [2+, 1 -] E(SAverage) = 0. 91829 STall = [0+, 2 -] E(STall) = 0 SShort = [1+, 2 -] E(SShort) = 0. 91829 Gain(S, Height) = 0. 95443 – [(3/8)*0. 91829 + (2/8)*0 + (3/8)*0. 91829] = 0. 26571 For attribute ‘Weight’: Values(Weight) : [Light, Average, Heavy] SLight = [1+, 1 -] E(SLight) = 1 SAverage = [1+, 2 -] E(SAverage) = 0. 91829 SHeavy = [1+, 2 -] E(SHeavy) = 0. 91829 Gain(S, Weight) = 0. 95443 – [(2/8)*1 + (3/8)*0. 91829] = 0. 01571 For attribute ‘Lotion’: Values(Lotion) : [Yes, No] SYes = [0+, 3 -] E(SYes) = 0 SNo = [3+, 2 -] E(SNo) = 0. 97095 Gain(S, Lotion) = 0. 95443 – [(3/8)*0 + (5/8)*0. 97095] = 0. 01571

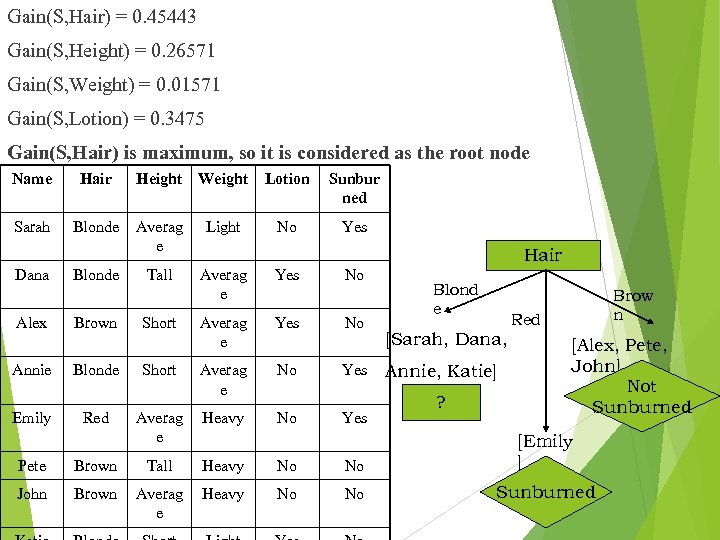Gain(S, Hair) = 0. 45443 Gain(S, Height) = 0. 26571 Gain(S, Weight) = 0. 01571 Gain(S, Lotion) = 0. 3475 Gain(S, Hair) is maximum, so it is considered as the root node Name Hair Sarah Blonde Dana Alex Blonde Brown Height Weight Lotion Sunbur ned No Yes Averag e Light Tall Averag e Yes Short No No Annie Blonde Short Averag e No Yes Emily Red Averag e Heavy No Yes Hair Blond e Red [Sarah, Dana, Annie, Katie] ? Brow n [Alex, Pete, John] Not Sunburned Pete Brown Tall Heavy No No [Emily ] John Brown Averag e Heavy No No Sunburned

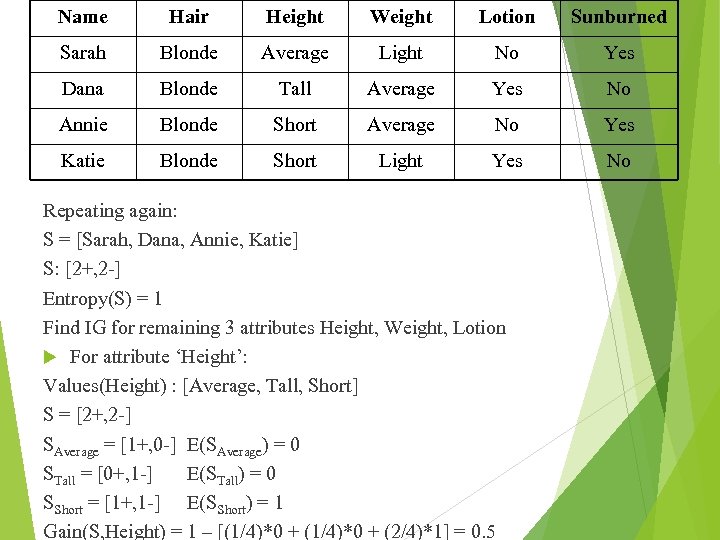Name Hair Height Weight Lotion Sunburned Sarah Blonde Average Light No Yes Dana Blonde Tall Average Yes No Annie Blonde Short Average No Yes Katie Blonde Short Light Yes No Repeating again: S = [Sarah, Dana, Annie, Katie] S: [2+, 2 -] Entropy(S) = 1 Find IG for remaining 3 attributes Height, Weight, Lotion For attribute ‘Height’: Values(Height) : [Average, Tall, Short] S = [2+, 2 -] SAverage = [1+, 0 -] E(SAverage) = 0 STall = [0+, 1 -] E(STall) = 0 SShort = [1+, 1 -] E(SShort) = 1 Gain(S, Height) = 1 – [(1/4)*0 + (2/4)*1] = 0. 5

For attribute ‘Weight’: Values(Weight) : [Average, Light] S = [2+, 2 -] SAverage = [1+, 1 -] E(SAverage) = 1 SLight = [1+, 1 -] E(SLight) = 1 Gain(S, Weight) = 1 – [(2/4)*1 + (2/4)*1]= 0 For attribute ‘Lotion’: Values(Lotion) : [Yes, No] S = [2+, 2 -] SYes = [0+, 2 -] E(SYes) = 0 SNo = [2+, 0 -] E(SNo) = 0 Gain(S, Lotion) = 1 – [(2/4)*0 + (2/4)*0]= 1 Therefore, Gain(S, Lotion) is maximum

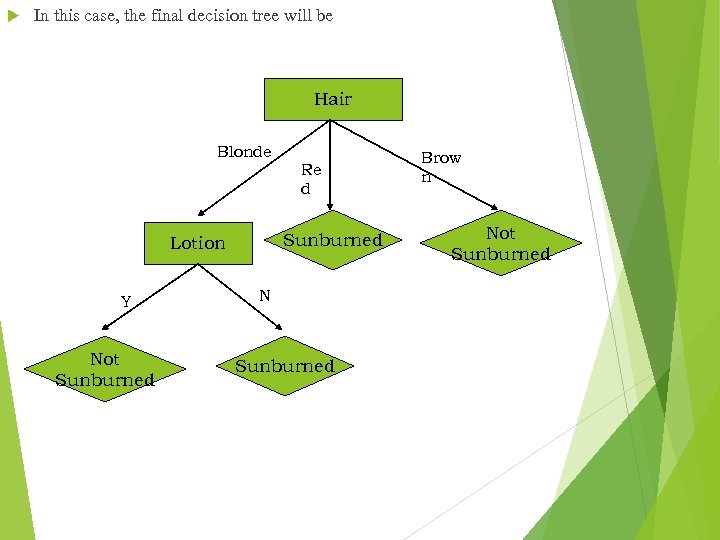In this case, the final decision tree will be Hair Blonde Re d Sunburned Lotion Y Not Sunburned N Sunburned Brow n Not Sunburned

Computing Information-Gain for Continuous-Valued Attributes Let attribute A be a continuous-valued attribute Must determine the best split point for A Sort the value A in increasing order Typically, the midpoint between each pair of adjacent values is considered as a possible split point (ai+ai+1)/2 is the midpoint between the values of ai and ai+1 The point with the minimum expected information requirement for A is selected as the split-point for A Split: D 1 is the set of tuples in D satisfying A ≤ split-point, and D 2 is the set of tuples in D satisfying A > split-point

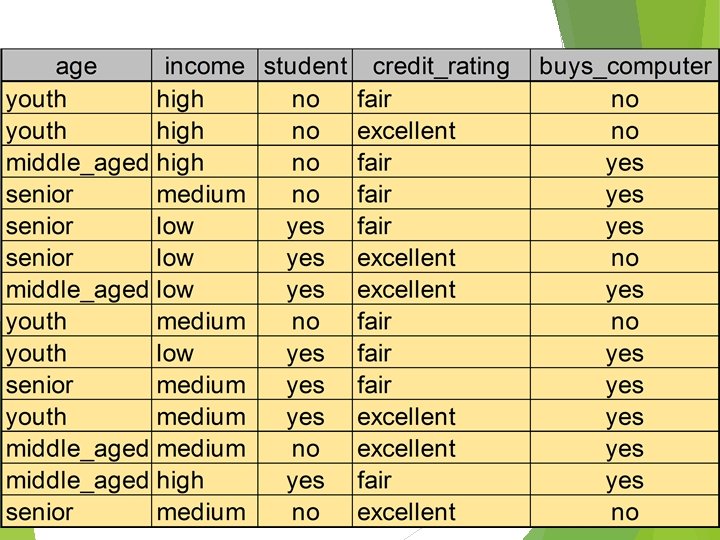
Gain Ratio for Attribute Selection (C 4. 5) Information gain measure is biased towards attributes with a large number of values C 4. 5 (a successor of ID 3) uses gain ratio to overcome the problem (normalization to information gain) Gain. Ratio(A) = Gain(A)/Split. Info(A) Ex. gain_ratio(income) = 0. 029/1. 557 = 0. 019 The attribute with the maximum gain ratio is selected as the splitting attribute

Gini Index (CART, IBM Intelligent. Miner) If a data set D contains examples from n classes, gini index, gini(D) is defined as where pj is the relative frequency of class j in D If a data set D is split on A into two subsets D 1 and D 2, the gini index gini(D) is defined as Reduction in Impurity: The attribute provides the smallest ginisplit(D) (or the largest reduction in impurity) is chosen to split the node (need to enumerate all the possible splitting points for each attribute)

Computation of Gini Index Ex. D has 9 tuples in buys_computer = “yes” and 5 in “no” Suppose the attribute income partitions D into 10 in D 1: {low, medium} and 4 in D 2 Gini{low, high} is 0. 458; Gini{medium, high} is 0. 450. Thus, split on the {low, medium} (and {high}) since it has the lowest Gini index All attributes are assumed continuous-valued May need other tools, e. g. , clustering, to get the possible split values Can be modified for categorical attributes

Comparing Attribute Selection Measures The three measures, in general, return good results but Information gain: biased towards multivalued attributes Gain ratio: tends to prefer unbalanced splits in which one partition is much smaller than the others Gini index: biased to multivalued attributes has difficulty when # of classes is large tends to favor tests that result in equal-sized partitions and purity in both partitions

Other Attribute Selection Measures CHAID: a popular decision tree algorithm, measure based on χ2 test for independence C-SEP: performs better than info. gain and gini index in certain cases G-statistic: has a close approximation to χ2 distribution MDL (Minimal Description Length) principle (i. e. , the simplest solution is preferred): The best tree as the one that requires the fewest # of bits to both (1) encode the tree, and (2) encode the exceptions to the tree Multivariate splits (partition based on multiple variable combinations) CART: finds multivariate splits based on a linear comb. of attrs. Which attribute selection measure is the best? Most give good results, none is significantly superior than others

Preparing Data for Classification and Prediction Data Cleaning : remove or reduce noise (apply smoothing) and treatment of missing values (replacing a missing value with the most commonly occurring values for that attribute, or with the most probable value based on statistics) Relevance Analysis : 1) Correlation analysis is used to check whether any two given attributes are statistically related. 2) Dataset may also contain irrelevant attributes. These kind of attributes may otherwise slow down and possibly mislead the learning step. Data Transformation and Reduction : may be transformed by normalization – scaling attributes such that it comes in one range. Or by generalizing it to higher-level concepts.

Advantage of ID 3 Understandable prediction rules are created from the training data. Builds the fastest tree. Builds a short tree. Only need to test enough attributes until all data is classified. Finding leaf nodes enables test data to be pruned, reducing number of tests.

Disadvantage of ID 3 Data may be over-fitted or over-classified, if a small sample is tested. Only one attribute at a time is tested for making a decision. Classifying continuous data may be computationally expensive, as many trees must be generated to see where to break the continuum.

Bayes’ Theorem: Basics Total probability Theorem: Bayes’ Theorem: Let X be a data sample (“evidence”): class label is unknown Let H be a hypothesis that X belongs to class C Classification is to determine P(H|X), (i. e. , posteriori probability): the probability that the hypothesis holds given the observed data sample X P(H) (prior probability): the initial probability E. g. , X will buy computer, regardless of age, income, … P(X): probability that sample data is observed P(X|H) (likelihood): the probability of observing the sample X, given that the hypothesis holds E. g. , Given that X will buy computer, the prob. that X is 31. . 40, medium income

Prediction Based on Bayes’ Theorem Given training data X, posteriori probability of a hypothesis H, P(H|X), follows the Bayes’ theorem Informally, this can be viewed as posteriori = likelihood x prior/evidence Predicts X belongs to Ci iff the probability P(Ci|X) is the highest among all the P(Ck|X) for all the k classes Practical difficulty: It requires initial knowledge of many probabilities, involving significant computational cost

Classification Is to Derive the Maximum Posteriori Let D be a training set of tuples and their associated class labels, and each tuple is represented by an n-D attribute vector X = (x 1, x 2, …, xn) Suppose there are m classes C 1, C 2, …, Cm. Classification is to derive the maximum posteriori, i. e. , the maximal P(Ci|X) This can be derived from Bayes’ theorem Since P(X) is constant for all classes, only needs to be maximized

Naïve Bayes Classifier A simplified assumption: attributes are conditionally independent (i. e. , no dependence relation between attributes): This greatly reduces the computation cost: Only counts the class distribution If Ak is categorical, P(xk|Ci) is the # of tuples in Ci having value xk for Ak divided by |Ci, D| (# of tuples of Ci in D) If Ak is continous-valued, P(xk|Ci) is usually computed based on Gaussian distribution with a mean μ and standard deviation σ and P(xk|Ci) is