DECISION SUPPORT SYSTEMS FOR PLANNING AND SCHEDULING IN

DECISION SUPPORT SYSTEMS FOR PLANNING AND SCHEDULING IN PRACTICE Michael Pinedo Stern School of Business New York University

DECISION SUPPORT SYSTEMS FOR PLANNING AND SCHEDULING IN PRACTICE I. Application Areas, Infrastructures, General Architectural Issues II. System Requirements III. Planning and Scheduling Techniques IV. System Implementations Commercial Packages

Part I. Application Areas, Infrastructures, General Architectural Issues

• Application Areas – Planning and Scheduling in Manufacturing and Services • Infrastructures – In Manufacturing – In Supply Chain Management – In Services • General Issues regarding – Systems Architecture – For Production Scheduling – For Workforce Scheduling

APPLICATION AREAS OF PLANNING AND SCHEDULING • Manufacturing – Process – Discrete – Automotive – Food and Snacks • Services: – Crew Scheduling (Airlines) – Workforce Scheduling (Call Centers) – Reservation Systems and Yield Management

INFORMATION SYSTEM INFRASTRUCTURE IN MANUFACTURING ENVIRONMENTS • Interfaces with Forecasting, Medium Term, and Long Term Planning • Interfaces with Product Design and Facility Layout

INFORMATION SYSTEM INFRASTRUCTURE IN SERVICE ENVIRONMENTS • Workforce Scheduling in – Cell Centers – Hospitals • Reservation Systems in – Airlines – Hotels – Car Rentals

Part II. Important Issues in Design of Decision Support Systems

IMPORTANT ISSUES IN DESIGN OF DECISION SUPPORT SYSTEMS • Module Design and Interfacing • GUI Design • Design of Link Between GUI and Algorithm Library • Internal Reoptimization • External Reoptimization

MODULAR (OBJECT-ORIENTED) DESIGN Standardization of Data Transfers Between Modules. Data Concerning: – Jobs (Operations) – Work Centers (Machines) – Schedules Have to be Properly Organized in order to make Transfer of Data Easy. EXAMPLE: Plugging in New Algorithm in Existing System should be Easy.

GUI’S SHOULD ALLOW: • Interactive Optimization – Freezing Jobs and Reoptimize – Creating New Schedules by Combining Different Parts from Different Schedules • Cascading and Propagation Effects After a Change or Mutation by the User, the System – does Feasibility Analysis – takes care of Cascading and Propagation Effects, – does Internal Reoptimization

GRAPHICS USER INTERFACES FOR SCHEDULING PRODUCTION PROCESSES • • Gantt Chart Interface Dispatch List Interface Time Buckets Throughput Diagrams

IMPORTANT OBJECTIVES TO BE DISPLAYED • Due Date Related – Number of Late Jobs – Maximum Lateness – Average Lateness • Productivity and Inventory Related – Total Setup Time – Total Machine Idle Time – Average Time Jobs Remain in System

SEQUENCE DEPENDENT SETUP TIMES Sijk = The Time it Takes to Setup for Job k at the Completion of Job j on Machine i. • One way to Retrieve These Data is Through a Table Look-up • Another way is Through a Formula Job j Carries a Number of Parameters in its Data String aij, bij, cij (color, sizes, etc. ) Sijk = fi (aij, aik) + gi (bij, bik) + hi (cij, cik) or Sijk = MAX (f. I (aij, aik), gi (bij, bik), hi (cij, cik))

INTERNAL RE OPTIMIZATION AFTER A CHANGE BY THE USER Internal Reoptimization Should Satisfy Certain Conditions: C. U. = Change by the User I. R. = Internal Reoptimization Internal Reoptimizaton Should be Reversible C. U. I. R. Reverse C. U. I. R. Original Schedule Internal Reoptimization Should be Commutative C. U. 1 I. R. C. U. 2 I. R. Same Schedule C. U. 2 I. R. C. U. 1 I. R.

Part III. Planning and Scheduling Optimization Techniques

PLANNING AND SCHEDULING OPTIMIZATION TECHNIQUES • • Dispatching Rules Composite Dispatching Rules Dynamic Programming Integer Programming Column Generation Branch and Bound Beam Search

PLANNING AND SCHEDULING OPTIMIZATION TECHNIQUES (continued) • Local Search • Decomposition Techniques – Temporal – Machine (Shifting Bottleneck) • Drum-Buffer-Rope • Hybrid Methods

IMPORTANT CHARACTERISTICS OF OPTIMIZATION TECHNIQUES • Quality of Solutions Obtained (How Close to Optimal? ) • Amount of CPU-Time Needed (Real-Time on a PC? ) • Ease of Development and Implementation (How much time needed to code, test, adjust and modify)

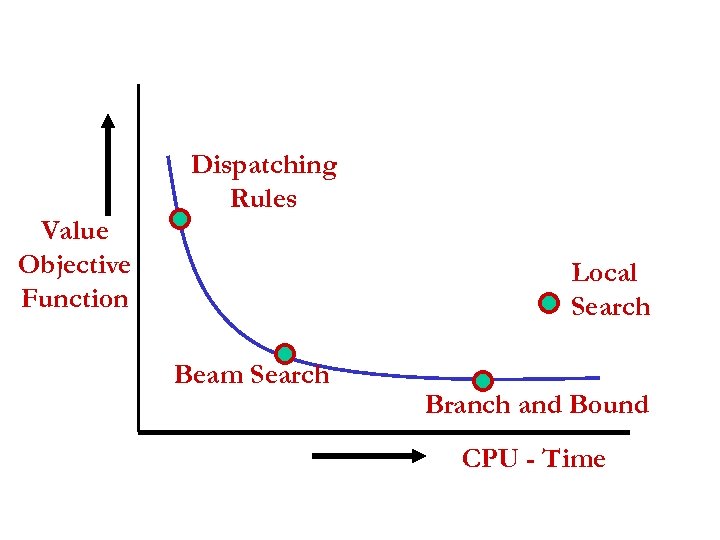Dispatching Rules Value Objective Function Local Search Beam Search Branch and Bound CPU - Time

COMPOSITE PRIORITY RULE THAT IS MIXTURE OF THREE BASIC PRIORITY RULES: • Weighted Shortest Processing Time First • Earliest Due Date First • Shortest Setup Time First

DYNAMIC PROGRAMMING Characterizing Equations: (i) Initial Conditions (ii) Recursive Relation (iii) Optimal Value Function Example: Consider a Single Machine and Objective Function Let J Denote a Subset of the n Jobs. Assume J is Processed First. Let V(J) = hj (Cj)

Initial Conditions: V({j}) = hj (pj) j = 1, …, n Recursive Relation: V(J) = min (V(J- {j}) + hj( pk)) j J Optimal Value Function: V({1, …. , n})

INTEGER PROGRAMMING FORMULATIONS • Hard Problems can often be Formulated as I. P. s. • These I. P. s are often Solved via Branch and Bound • Many Applications of I. P. Formulations in – Workforce scheduling – Crew Scheduling

I. P. FORMULATION OF WORKFORCE SCHEDULING PROBLEM • • Predetermined Cycle of m Periods During Period i presence of bi needed n Different Shift Patterns Shift Pattern j a 1 j 0 a 2 j. . . amj 1 1 1 0 0 • cj is Cost of Assigning one Person to Shift j • xj is Integer Decision Variable Representing Number Assigned to Shift j

MINIMIZE c 1 x 1 + c 2 x 2 + …. + cn xn SUBJECT TO: a 11 x 1 + a 12 x 2 + … + a 1 n xn > b 1 a 12 x 1 + a 22 x 2. . . am 1 x 1 + am 2 x 2 + … + amn xn > bm xj Integer

I. P. FORMULATION OF CREW SCHEDULING PROBLEM • m Jobs (Flight Legs) • n Feasible Combinations of Jobs one Crew can Handle (Round Trips) • cj Cost of Round Trip j • • INTEGER PROGRAM min c 1 x 1 + x 2 + …. + cn xn S. T. a 11 x 1 + a 12 x 2+ …. + ain xn > 1 am 1 x 1 + am 2 x 2+ …. + amn xn > 1 xj {0, 1} Each Column is a Round Trip Each Row is a Job that must be Covered SET PARTITIONING PROBLEM

DISJUNCTIVE PROGRAMMING FORMULATIONS • Hard Problems can often be Formulated as Disjunctive Programs • These Programs are often Solved via Branch and Bound • Many Applications of Disjunctive Programs in Job Shop Scheduling

MINIMIZING THE MAKESPAN IN A JOB SHOP pij = processing time of job j on machine i yij = starting time of job j on machine i DISJUNCTIVE PROGRAM Minimize Cmax Subject to ykj - yij > pij For All (i, j) (k, j) Cmax - yij > pij For All (i, j) yij - yiℓ > pi ℓ or yiℓ - yij > pij For All (i, ℓ) ( i, j) yij > 0 For All (i, j) There are Disjunctive Programs for Job Shops with other Objectives

LOCAL (NEIGHBORHOOD) SEARCH METHODS • Simulated Annealing (Probabilistic Method) • Tabu-Search (Deterministic Method) • Genetic Algorithms

IMPORTANT CHARACTERISTICS OF LOCAL SEARCH PROCEDURES • Schedule Representation Needed for Procedure • The Neighborhood Design • The Search Process within the Neighborhood • The Acceptance-Rejection Criterion

DECOMPOSITION TECHNIQUES • Machine Decomposition (Shifting Bottleneck Techniques) • Temporal Decomposition IMPORTANT CHARACTERISTICS OF DECOMPOSITION TECHNIQUES • Select as the next Subproblem to Solve always the one that Appears the Hardest (“Follow the Path of the Most Resistance”) • After the Completion of Each Step, Reoptimize all the Steps that were Done Before

HYBRID METHODS • Scheduling techniques can be Combined in Series • E. G. , FIRST USE A DISPATCHING RULE, THEN FOLLOW UP WITH A LOCAL SEARCH • Scheduling Techniques can be Combined in an Integrated Manner • E. G. , A DISPATCHING RULE CAN BE USED WITHIN A BRANCH AND BOUND TO OBTAIN UPPER BOUNDS. • DYNAMIC PROGRAMMING ROUTINE CAN BE USED FOR A SINGLE MACHINE SUBPROBLEM WITHIN A MACHINE DECOMPOSITION TECHNIQUE

Part IV. System Implementation Issues Commercial Packages

ERP-SYSTEMS SAP, Baan, JD Edwards, People Soft GENERAL OPTIMIZATION Ilog, Dash GENERAL SCHEDULING (Often in Framework of Supply Chain Management) I 2, Cybertec, Auto. Simulation, IDS Professor Scheer SCHEDULING OIL AND PROCESS INDUSTRIES Haverly Systems, Chesapeake, Finity SCHEDULING CONSUMER PRODUCTS Manugistics, Numetrix SCHEDULING WORKFORCE IN CALL CENTERS AIX, TCS, Siebel

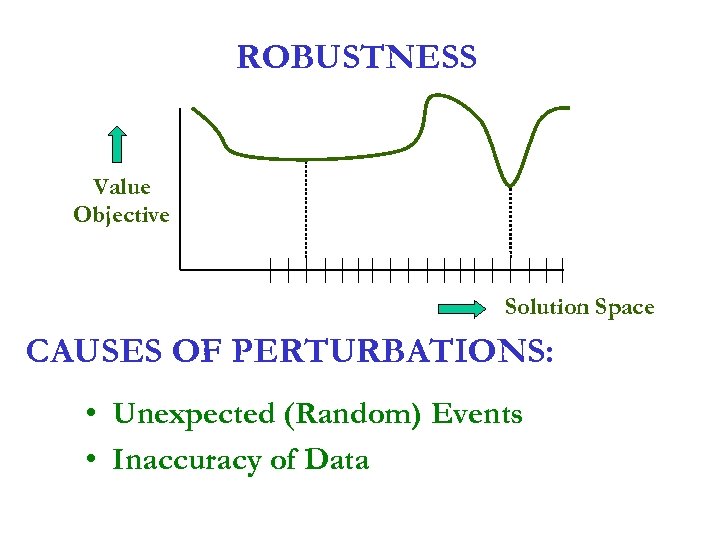ROBUSTNESS Value Objective Solution Space CAUSES OF PERTURBATIONS: • Unexpected (Random) Events • Inaccuracy of Data

MEASURES OF ROBUSTNESS • δ - Perturbation; Amount of Time Completion of a Task is Postponed • Z - Value of the Objective Under Original Schedule • Z 1 - Value of the Objective Under New Situation (without rescheduling) Z 1 - Z = L (δ) δ

OPTION: Reschedule After Perturbation • Local Rescheduling • Global Rescheduling PRACTICAL CONSIDERATION: • New Schedule Should be Similar to Old Schedule (Distance Measure)

RULES TO FOLLOW IN ORDER TO GENERATE ROBUST SCHEDULES • Insert Idle times (Especially Where Perturbations are to be Expected) • Less Flexible Job First More Flexible Jobs Later • Do NOT Postpone Processing when Possible (NOTE: This Would Go Against JIT Principles)

LEARNING MECHANISMS • Rote Learning (When Solution Space is Relatively Small) • Classifier Systems (Often Based on Genetic Algorithms) • Case Based Reasoning (Parameter Adjustment Methods) • Induction Methods and Neural Nets

PARAMETER ADJUSTMENT ATCS - Rule Ij (t, ℓ ) = wj exp (- (dj-pj-t)+) exp (- sℓ j) pj k 1 p k 2 s k 1 and k 2 are hard to determine k 1 and k 2 Functions of – Due Date tightness τ – Due Date Range R – Setup Time Severity η

ON-LINE LEARNING Every Time the Problem is Solved, the Problem is also Solved for k 1 + δ, k 1 - δ, k 2 + δ, k 2 - δ Dependent Upon the Outcome the Parameters are Adjusted for the Next Time.

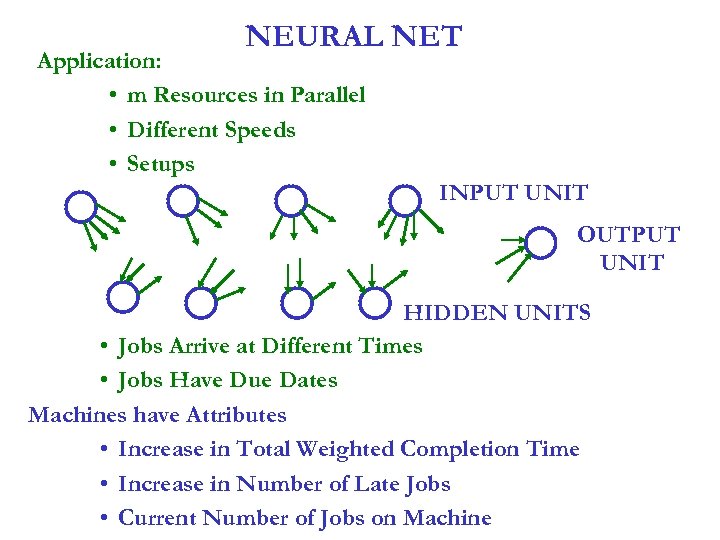NEURAL NET Application: • m Resources in Parallel • Different Speeds • Setups INPUT UNIT OUTPUT UNIT HIDDEN UNITS • Jobs Arrive at Different Times • Jobs Have Due Dates Machines have Attributes • Increase in Total Weighted Completion Time • Increase in Number of Late Jobs • Current Number of Jobs on Machine

OFF-LINE TRAINING BY AN EXPERT Expert Plus Learning Algorithm (Back Propagation) Determine the Connection Weights

MULTIPLE OBJECTIVES EXAMPLE: • m Resources in Parallel • n Jobs • Due Dates • Sequence Dependent Setups OBJECTIVES: • Minimize Sum of Setup Times • Minimize Penalties Due to Late Delivery Weights of the Two Objectives Vary over Time and Depend on Status Quo.

GENERAL FRAMEWORK: • Mixing of Priority Rules • Switching Over Between Rules Scaling Parameters and Switch-Over Times Depend on the Data Set Framework Above can be Combined with Local Search Heuristic.

DESIGN ISSUES WITH REGARD TO DECISION SUPPORT SYSTEMS FOR PLANNING AND SCHEDULING Michael Pinedo Stern School of Business New York University • Robustness • Multiple Objectives • Learning mechanisms

DECISION SUPPORT SYSTEMS • • Forecasting Facility Location Supply Chain Management Routing and Distribution

PLANNING AND SCHEDULING • Characteristics: – Engines Often Based on Combinatorial Algorithms – Systems Often have to Operate in Real Time

IMPORTANCE OF PLANNING AND SCHEDULING SYSTEMS • 150 Software Companies – I 2 – Manugistics – Bender-Synquest – IDS - Scheer – SAP – Bran

PLANNING AND SCHEDULING FRAMEWORK • • Resources (Machines) Tasks (Jobs) Due Dates Objectives GOAL: • Determine a Schedule (solution) That Minimizes the Objective(s)