5a36c905f02eb7687251ec01b44fa031.ppt
- Количество слайдов: 41

Decision-Procedure Based Theorem Provers Tactic-Based Theorem Proving Inferring Loop Invariants CS 294 -8 Lecture 12 Prof. Necula CS 294 -8 Lecture 12 1
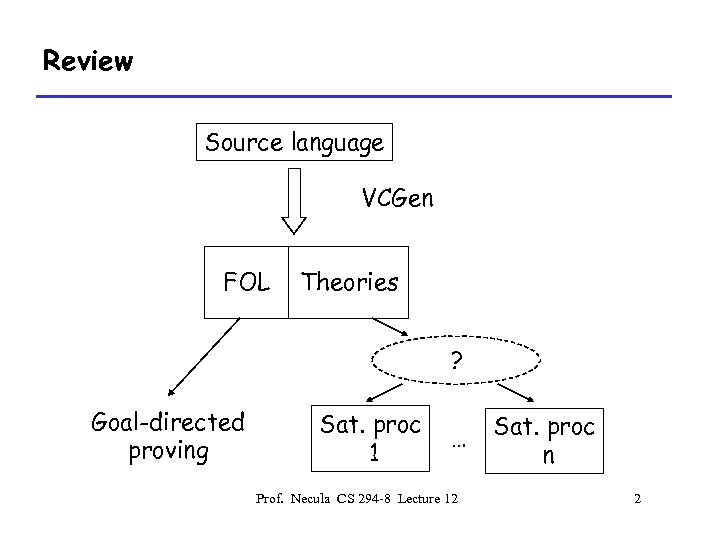
Review Source language VCGen FOL Theories ? Goal-directed proving Sat. proc 1 … Prof. Necula CS 294 -8 Lecture 12 Sat. proc n 2

Combining Satisfiability Procedures • Consider a set of literals F – Containing symbols from two theories T 1 and T 2 • We split F into two sets of literals – F 1 containing only literals in theory T 1 – F 2 containing only literals in theory T 2 – We name all subexpressions: p 1(f 2(E)) is split into f 2(E) = n p 1(n) • We have: unsat (F 1 F 2) iff unsat(F) – unsat(F 1) unsat(F 2) unsat(F) – But the converse is not true • So we cannot compute unsat(F) with a trivial combination of the sat. procedures for T 1 and T 2 Prof. Necula CS 294 -8 Lecture 12 3

Combining Satisfiability Procedures. Example • Consider equality and arithmetic f(f(x) - f(y)) f(z) x y y+z x x=y 0 z y x f(x) = f(y) f(x) - f(y) = z false 0=z f(f(x) - f(y)) = f(z) Prof. Necula CS 294 -8 Lecture 12 4

Combining Satisfiability Procedures • Combining satisfiability procedures is non trivial • And that is to be expected: – Equality was solved by Ackerman in 1924, arithmetic by Fourier even before, but E + A only in 1979 ! • Yet in any single verification problem we will have literals from several theories: – Equality, arithmetic, lists, … • When and how can we combine separate satisfiability procedures? Prof. Necula CS 294 -8 Lecture 12 5
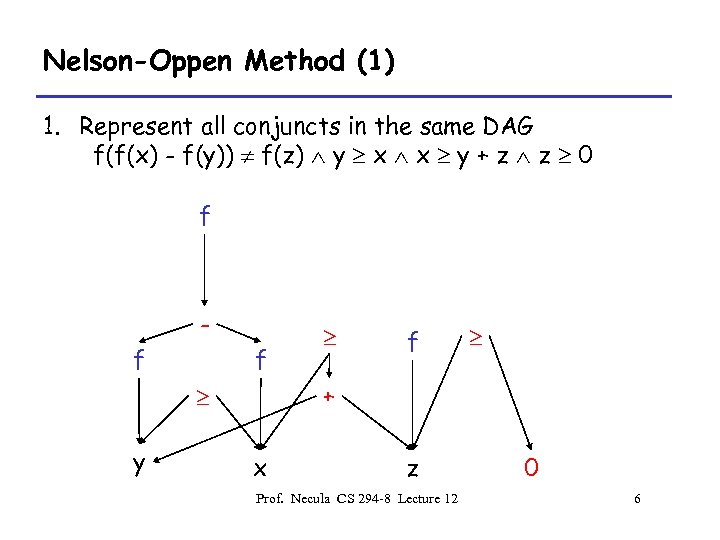
Nelson-Oppen Method (1) 1. Represent all conjuncts in the same DAG f(f(x) - f(y)) f(z) y x x y + z z 0 f f + y x z Prof. Necula CS 294 -8 Lecture 12 0 6
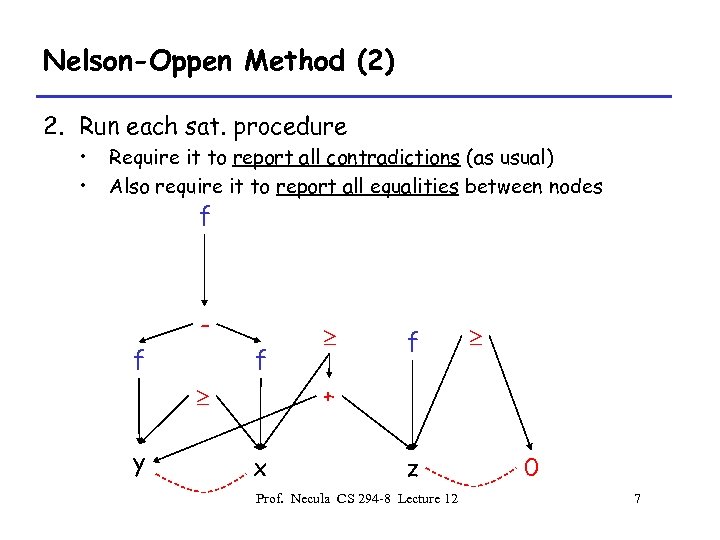
Nelson-Oppen Method (2) 2. Run each sat. procedure • • Require it to report all contradictions (as usual) Also require it to report all equalities between nodes f f + y x z Prof. Necula CS 294 -8 Lecture 12 0 7
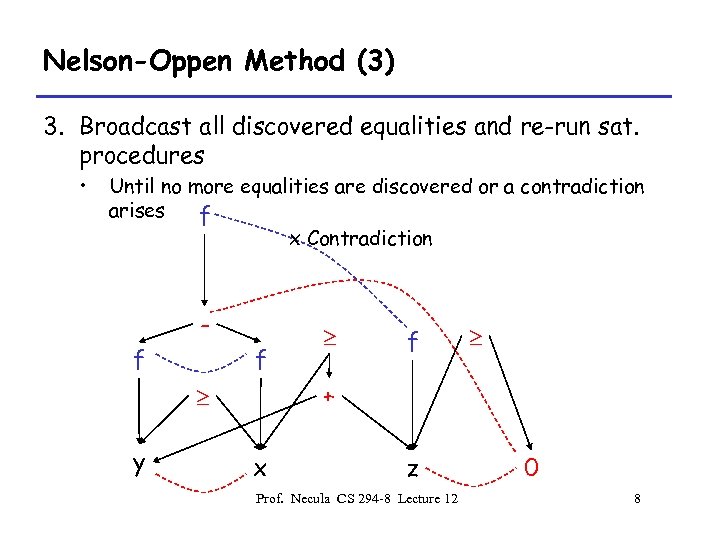
Nelson-Oppen Method (3) 3. Broadcast all discovered equalities and re-run sat. procedures • Until no more equalities are discovered or a contradiction arises f x Contradiction f f f + y x z Prof. Necula CS 294 -8 Lecture 12 0 8

What Theories Can be Combined? • Only theories without common interpreted symbols – But Ok if one theory takes the symbol uninterpreted • Only certain theories can be combined – – Consider (Z, +, ·) and Equality Consider: 1 x 2 a = 1 b = 2 f(x) f(a) f(x) f(b) No equalities and no contradictions are discovered Yet, unsatisfiable • A theory is non-convex when a set of literals entails a disjunction of equalities without entailing any single equality Prof. Necula CS 294 -8 Lecture 12 9

Handling Non-Convex Theories • Many theories are non-convex • Consider theory of memory and pointers – It is not-convex: true A = A’ sel(upd(M, A, V), A’) = sel(M, A’) (neither of the disjuncts is entailed individually) • For such theories it can be the case that – No contradiction is discovered – No single equality is discovered – But a disjunction of equalities is discovered • We need to propagate disjunction of equalities … Prof. Necula CS 294 -8 Lecture 12 10

Propagating Disjunction of Equalities • To propagate disjunctions we perform a case split: • If a disjunction E 1 … En is discovered: Save the current state of the prover for i = 1 to n { broadcast Ei if no contradiction arises then return “satisfiable” restore the saved prover state } return “unsatisfiable” Prof. Necula CS 294 -8 Lecture 12 11

Handling Non-Convex Theories • Case splitting is expensive – Must backtrack (performance --) – Must implement all satisfiability procedures in incremental fashion (simplicity --) • In some cases the splitting can be prohibitive: – Take pointers for example. upd(…(upd(m, i 1, x), …, in-1, x), in, x) = upd(…(upd(m, j 1, x), …, jn-1, x) sel(m, i 1) x … sel(m, in) x entails j k ij ik (a conjunction of length n entails n 2 disjuncts) Prof. Necula CS 294 -8 Lecture 12 12

Forward vs. Backward Theorem Proving Prof. Necula CS 294 -8 Lecture 12 13

Forward vs. Backward Theorem Proving • The state of a prover can be expressed as: H 1 … Hn ? G – Given the hypotheses Hi try to derive goal G • A forward theorem prover derives new hypotheses, in hope of deriving G – If H 1 … Hn H then move to state H 1 … Hn H ? G – Success state: H 1 … G … Hn ? G • A forward theorem prover uses heuristics to reach G – Or it can exhaustively derive everything that is derivable ! Prof. Necula CS 294 -8 Lecture 12 14

Forward Theorem Proving • Nelson-Oppen is a forward theorem prover: – – The state is L 1 … Ln L ? false If L 1 … Ln L E (an equality) then New state is L 1 … Ln L E ? false (add the equality) Success state is L 1 … L … Ln ? false • Nelson-Oppen provers exhaustively produce all derivable facts hoping to encounter the goal • Case splitting can be explained this way too: – If L 1 … Ln L E E’ (a disjunction of equalities) then – Two new states are produced (both must lead to success) L 1 … Ln L E ? false L 1 … Ln L E’ ? false Prof. Necula CS 294 -8 Lecture 12 15

Backward Theorem Proving • A backward theorem prover derives new subgoals from the goal – The current state is H 1 … Hn ? G – If H 1 … Hn G 1 … Gn G (Gi are subgoals) – Produce “n“ new states (all must lead to success): H 1 … Hn ? G i • Similar to case splitting in Nelson-Oppen: – Consider a non-convex theory: H 1 … Hn E E’ is same as H 1 … Hn E E’ false (thus we have reduced the goal “false” to subgoals E E’ ) Prof. Necula CS 294 -8 Lecture 12 16

Programming Theorem Provers • Backward theorem provers most often use heuristics • If it useful to be able to program the heuristics • Such programs are called tactics and tactic-based provers have this capability – E. g. the Edinburgh LCF was a tactic based prover whose programming language was called the Meta-Language (ML) • A tactic examines the state and either: – Announces that it is not applicable in the current state, or – Modifies the proving state Prof. Necula CS 294 -8 Lecture 12 17

Programming Theorem Provers. Tactics. • State = Formula list Formula – A set of hypotheses and a goal • Tactic = State (State a) (unit a) a – Continuation passing style – Given a state will invoke either the success continuation with a modified state or the failure continuation • Example: a congruence-closure based tactic cc (h, g) c f = let e 1, …, en new equalities in the congruence closure of h c (h {e 1, …, en}, g) – A forward chaining tactic Prof. Necula CS 294 -8 Lecture 12 18

Programming Theorem Provers. Tactics. • Consider an axiom: x. a(x) b(x) – Like the clause b(x) : - a(x) in Prolog • This could be turned into a tactic clause (h, g) c f = if unif(g, b) = f then s (h, f(a)) else f () – A backward chaining tactic Prof. Necula CS 294 -8 Lecture 12 19

Programming Theorem Provers. Tacticals. • Tactics can be composed using tacticals Examples: • THEN : tactic THEN t 1 t 2 = ls. lc. lf. let newc s’ = t 2 s’ c f in t 1 s newc f • REPEAT : tactic REPEAT t = THEN t (REPEAT t) • ORELSE : tactic ORELSE t 1 t 2 = ls. lc. lf. let newf x = t 2 s c f in t 1 s c newf Prof. Necula CS 294 -8 Lecture 12 20

Programming Theorem Provers. Tacticals • Prolog is just one possible tactic: – Given tactics for each clause: c 1, …, cn – Prolog : tactic Prolog = REPEAT (c 1 ORLESE c 2 ORELSE … ORELSE cn) • Nelson-Oppen can also be programmed this way – The result is not as efficient as a special-purpose implementation • This is a very powerful mechanism for semi-automatic theorem proving – Used in: Isabelle, HOL, and many others Prof. Necula CS 294 -8 Lecture 12 21

Techniques for Inferring Loop Invariants Prof. Necula CS 294 -8 Lecture 12 22

Inferring Loop Invariants • Traditional program verification has several elements: – Function specifications and loop invariants – Verification condition generation – Theorem proving • Requiring specifications from the programmer is often acceptable • Requiring loop invariants is not acceptable – Same for specifications of local functions Prof. Necula CS 294 -8 Lecture 12 23

Inferring Loop Invariants • A set of cutpoints is a set of program points : – There is at least one cutpoint on each circular path in CFG – There is a cutpoint at the start of the program – There is a cutpoint before the return • Consider that our function uses n variables x: • We associate with each cutpoint an assertion Ik(x) • If a is a path from cutpoint k to j then : – Ra(x) : Zn expresses the effect of path a on the values of x at j as a function of those at k – Pa(x) : Zn B is a path predicate that is true exactly of those values of x at k that will enable the path a Prof. Necula CS 294 -8 Lecture 12 24
![Cutpoints. Example. 0 L = len(A) K=0 S=0 1 S = S + A[K] Cutpoints. Example. 0 L = len(A) K=0 S=0 1 S = S + A[K]](https://present5.com/presentation/5a36c905f02eb7687251ec01b44fa031/image-25.jpg)
Cutpoints. Example. 0 L = len(A) K=0 S=0 1 S = S + A[K] K ++ K<L 2 return S • p 01 = true r 01 = { A A, K 0, L len(A), S 0, m m} • p 11 = K + 1 < L r 11 = { A A, K K + 1, L L, S S + sel(m, A + K), m m} • p 12 = K + 1 L r 12 = r 11 • Easily obtained through sym. eval. Prof. Necula CS 294 -8 Lecture 12 25

Equational Definition of Invariants • A set of assertions is a set of invariants if: – The assertion for the start cutpoint is the precondition – The assertion for the end cutpoint is the postcondition – For each path from i to j we have x. Ii(x) Pij(x) Ij(Rij(x)) • Now we have to solve a system of constraints with the unknowns I 1, …, In-1 – I 0 and In are known • We will consider the simpler case of a single loop – Otherwise we might want to try solving the inner/last loop first Prof. Necula CS 294 -8 Lecture 12 26
![Invariants. Example. 0 L = len(A) K=0 S=0 1 S = S + A[K] Invariants. Example. 0 L = len(A) K=0 S=0 1 S = S + A[K]](https://present5.com/presentation/5a36c905f02eb7687251ec01b44fa031/image-27.jpg)
Invariants. Example. 0 L = len(A) K=0 S=0 1 S = S + A[K] K ++ K<L 2 1. I 0 I 1(r 0(x)) • The invariant I 1 is established initially ro 2. I 1 K+1 < L I 1(r 1(x)) • The invariant I 1 is preserved in the loop r 1 • I 1 K+1 L I 2(r 1(x)) • The invariant I 1 is strong enough (i. e. useful)h return S Prof. Necula CS 294 -8 Lecture 12 27
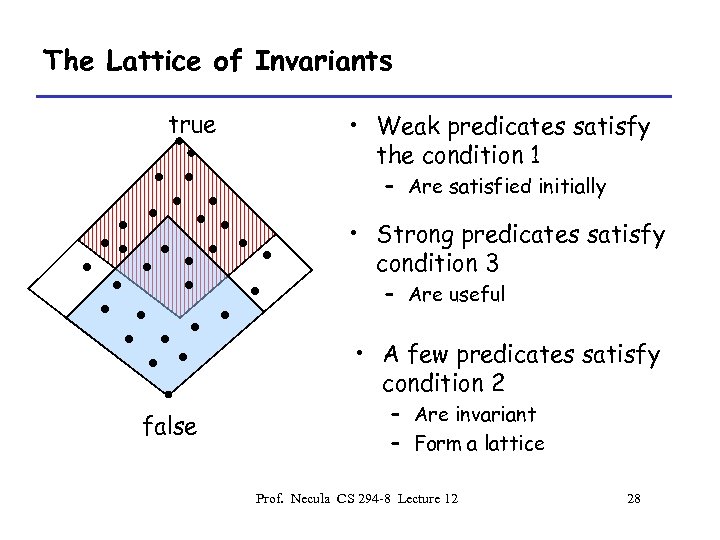
The Lattice of Invariants true • Weak predicates satisfy the condition 1 – Are satisfied initially • Strong predicates satisfy condition 3 – Are useful • A few predicates satisfy condition 2 false – Are invariant – Form a lattice Prof. Necula CS 294 -8 Lecture 12 28

Finding The Invariant • Which of the potential invariants should we try to find ? • We prefer to work backwards – Essentially proving only what is needed to satisfy In – Forward is also possible but sometimes wasteful since we have to prove everything that holds at any point Prof. Necula CS 294 -8 Lecture 12 29
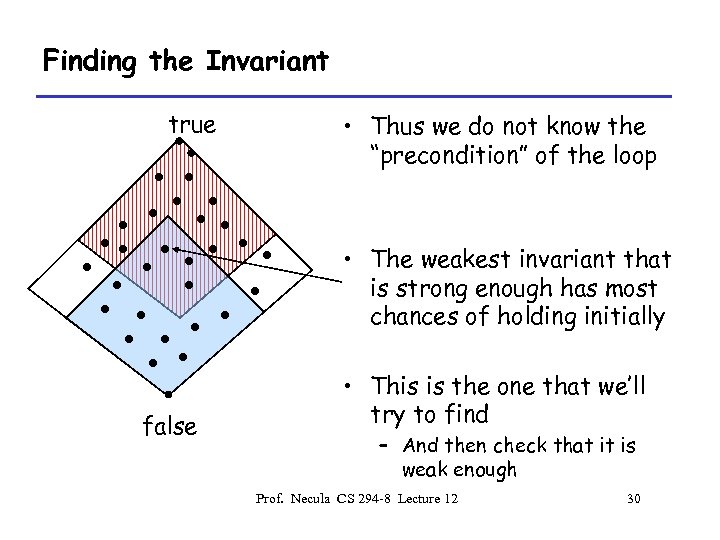
Finding the Invariant true • Thus we do not know the “precondition” of the loop • The weakest invariant that is strong enough has most chances of holding initially false • This is the one that we’ll try to find – And then check that it is weak enough Prof. Necula CS 294 -8 Lecture 12 30
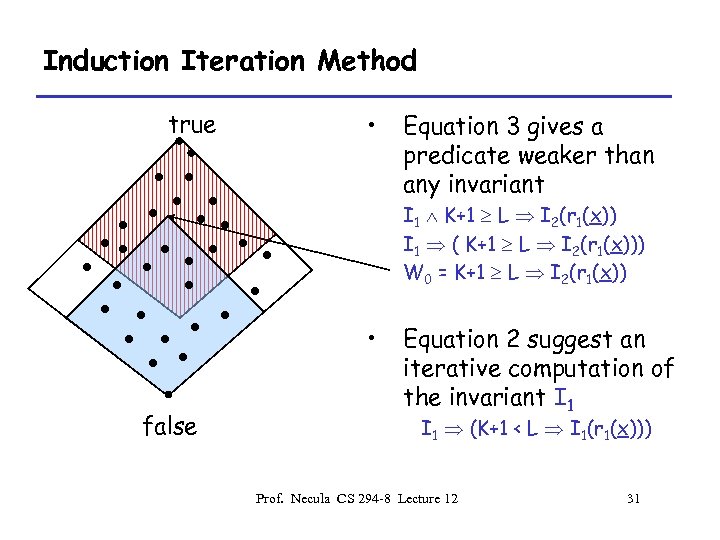
Induction Iteration Method true • Equation 3 gives a predicate weaker than any invariant I 1 K+1 L I 2(r 1(x)) I 1 ( K+1 L I 2(r 1(x))) W 0 = K+1 L I 2(r 1(x)) • false Equation 2 suggest an iterative computation of the invariant I 1 (K+1 < L I 1(r 1(x))) Prof. Necula CS 294 -8 Lecture 12 31

Induction Iteration Method • Define a family of predicates W 0 = K+1 L I 2(r 1(x)) Wj = W 0 K+1 < L Wj-1(r 1(x)) • Properties of Wj – Wj Wj-1 … W 0 (they form a strengthening chain) – I 1 Wj (they are weaker than any invariant) – If Wj-1 Wj then • Wj is an invariant (satisfies both equations 2 and 3): Wj K+1 < L Wj(r 1(x)) • Wj is the weakest invariant (recall domain theory, predicates form a domain, and we use the fixed point theorem to obtain least solutions to recursive equations) Prof. Necula CS 294 -8 Lecture 12 32

Induction Iteration Method W = K+1 L I 2(r 1(x)) // This is W 0 W’ = true while (not (W’ W)) { W’ = W W = (K+1 L I 2(r 1(x))) (K + 1 < L W’(r 1(x))) } • The only hard part is to check whether W’ W – We use a theorem prover for this purpose Prof. Necula CS 294 -8 Lecture 12 33
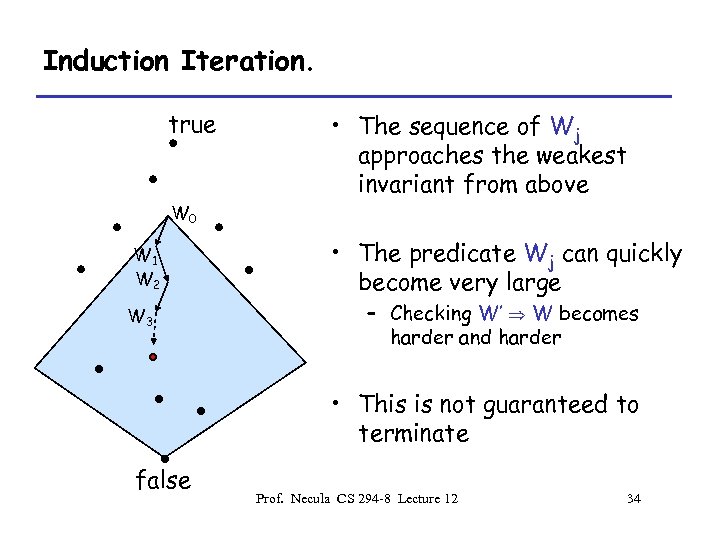
Induction Iteration. true W 0 W 1 W 2 W 3 • The sequence of Wj approaches the weakest invariant from above • The predicate Wj can quickly become very large – Checking W’ W becomes harder and harder • This is not guaranteed to terminate false Prof. Necula CS 294 -8 Lecture 12 34
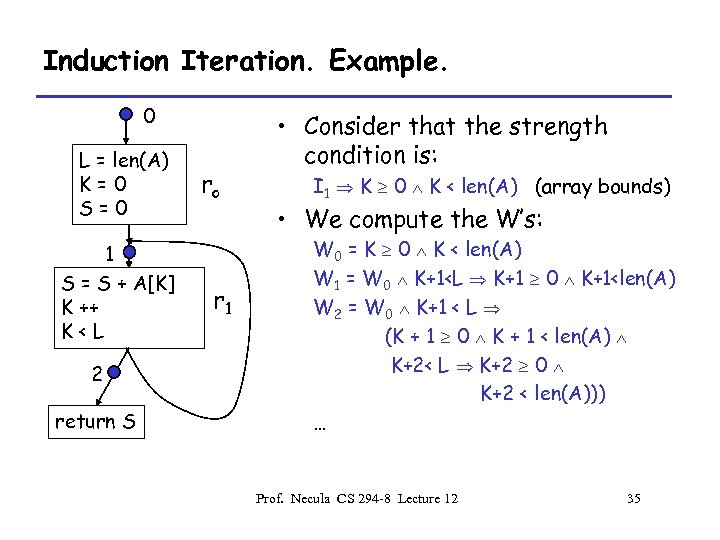
Induction Iteration. Example. 0 L = len(A) K=0 S=0 1 S = S + A[K] K ++ K<L 2 return S ro r 1 • Consider that the strength condition is: I 1 K 0 K < len(A) (array bounds) • We compute the W’s: W 0 = K 0 K < len(A) W 1 = W 0 K+1<L K+1 0 K+1<len(A) W 2 = W 0 K+1 < L (K + 1 0 K + 1 < len(A) K+2< L K+2 0 K+2 < len(A))) … Prof. Necula CS 294 -8 Lecture 12 35

Induction Iteration. Strengthening. • We can try to strengthen the inductive invariant • Instead of: Wj = W 0 K+1 < L Wj-1(r 1(x)) we compute: Wj = strengthen (W 0 K+1 < L Wj-1(r 1(x))) where strengthen(P) P • We still have Wj Wj-1 and we stop when Wj-1 Wj – The result is still an invariant that satisfies 2 and 3 Prof. Necula CS 294 -8 Lecture 12 36

Strengthening Heuristics • One goal of strengthening is simplification: – Drop disjuncts: P 1 P 2 P 1 – Drop implications: P 1 P 2 • A good idea is to try to eliminate variables changed in the loop body: – If Wj does not depend on variables changed by r 1 (e. g. K, S) – Wj+1 = W 0 K+1 < L Wj(r 1(x)) = W 0 K+1 < L Wj – Now Wj Wj+1 and we are done ! Prof. Necula CS 294 -8 Lecture 12 37
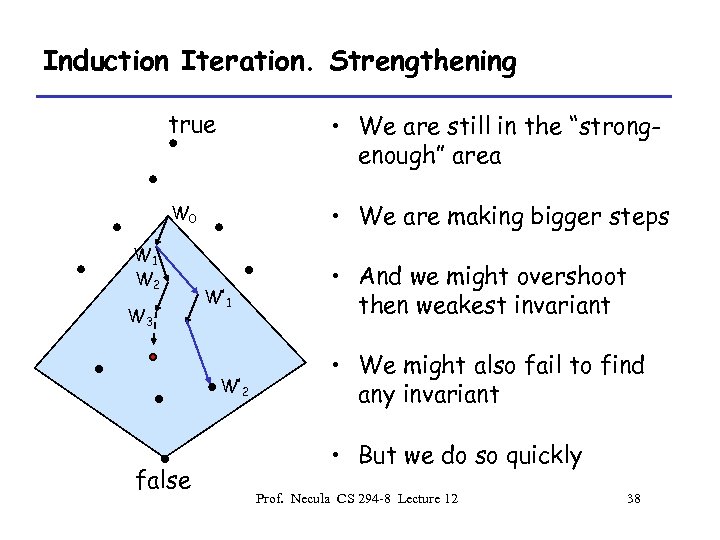
Induction Iteration. Strengthening true • We are still in the “strongenough” area W 0 • We are making bigger steps W 1 W 2 W 3 W’ 1 W’ 2 false • And we might overshoot then weakest invariant • We might also fail to find any invariant • But we do so quickly Prof. Necula CS 294 -8 Lecture 12 38

One Strengthening Heuristic for Integers • Rewrite Wj in conjunctive normal form W 1 = K 0 K < len(A) (K + 1 < L K + 1 0 K + 1 < len(A)) • Take each disjunction containing arithmetic literals = K 0 K < len(A) (K + 1 L – Negate it and obtain a conjunction of arithmetic literals K+1 < L K+1 len(A) – Weaken the result by eliminating a variable (preferably a loop -modified variable) E. g. , add the two literals: L > len(A) – Negate the result and get another disjunction: L len(A) W 1 = K 0 K < len(A) L len(A) (check that W 1 W 2) Prof. Necula CS 294 -8 Lecture 12 39

Induction Iteration • We showed a way to compute invariants algoritmically – Similar to fixed point computation in domains – Similar to abstract interpretation on the lattice of predicates • Then we discussed heuristics that improve the termination properties – Similar to widening in abstract interpretation Prof. Necula CS 294 -8 Lecture 12 40

Theorem Proving. Conclusions. • Theorem proving strengths – Very expressive • Theorem proving weaknesses – Too ambitious • A great toolbox for software analysis – Symbolic evaluation – Decision procedures • Related to program analysis – Abstract interpretation on the lattice of predicates Prof. Necula CS 294 -8 Lecture 12 41
5a36c905f02eb7687251ec01b44fa031.ppt