25cbb439576137efcb5f4dc1e0e7b041.ppt
- Количество слайдов: 68

DECISION MODELING WITH MICROSOFT EXCEL Chapter 12 Multi-Objective Decision Making and Heuristics Part 2 Copyright 2001 Prentice Hall Publishers and Ardith E. Baker

MULTIPLE OBJECTIVES In many applications, the planner has more than one ______. The presence of multiple objectives is frequently referred to as the problem of “_____ apples and oranges. ” Consider a corporate planner whose long-range goals are to: 1. Maximize discounted_____ 2. ______market share at the end of the planning period 3. Maximize existing physical _____at the end of the planning period

These goals are not _________(i. e. , they cannot be _____combined or compared). It is also clear that the goals are ______(i. e. , there are trade-offs in the sense that sacrificing the requirements on any one goal will tend to produce greater______ on the others. These models, although not applied as often in practice as some of the other models (such as linear programming, _______, inventory control, etc. ), have been found to be especially useful on problems in the________.

Several approaches to multiple objective models (also called _______decision making) have been developed: Multi-attribute ______theory Search for _____optimal solutions via multi-criteria linear programming Analytic Hierarchy Process (AHP) Developed by Thomas Saaty, AHP helps managers choose between many decision _______on the basis of multiple criteria. Goal Programming (GP) Introduced by A. Charnes and W. W. Cooper. GP is a ______approach to the multipleobjectives model. AHP and Goal Programming will be discussed.

GOAL PROGRAMMING Goal Programming is an extension of ______ Programming that enables the planner to come as close as possible to satisfying various _______and constraints. It allows the decision maker, at least in a heuristic sense, to incorporate his or her ______system in dealing with multiple conflicting goals. GP is sometimes considered to be an attempt to put into a mathematical _________context, the concept of satisficing. Coined by Herbert Simon, it communicates the idea that individuals often do not seek optimal solutions, but rather solutions that are “______” or “close enough. ”

Suppose that we have an ______program design model with decision variables x 1 and x 2, where x 1 is the hours of ________work x 2 is the hours of ________work Assume the following ______on total program hours: x 1 + x 2 < 100 (total program hours) Two Kinds of Constraints In the goal programming approach, there are two kinds of constraints: 1. ______constraints (so-called hard constraints) that cannot be violated. 2. _______constraints (so-called soft constraints) that may be violated if necessary.

Now, suppose that each hour of classroom work involves 12 minutes of _______experience and 19 minutes of _______problem solving Each hour of laboratory work involves 29 minutes of small-group experience and 11 minutes of individual problem solving The total _____time is at most 6, 000 minutes (100 hr * 60 min/hr). There are two goals: Each student should spend as close as possible to ¼ of the _______program time working in small groups and ¹/3 of the time on problem_______.

These conditions are: 12 x 1 + 29 x 2 ~ 1500 (small-group experience) = 1 2 19 x 1 + 11 x 2 ~ 2000 (individual problem solving) = Where ~ means that the left-hand side is desired to = be “_________” to the right-hand side. In order to satisfy the system constraint, at least one of the two goals will be_______. To ______the goal programming approach, the small-group experience condition is rewritten as the goal constraint: 12 x 1 + 29 x 2 + u 1 – v 1 = 1500 (u 1 > 0, v 1 > 0) Where u 1 = the amount by which total small-group experience falls short of 1500 v 1 = the amount by which total small-group experience exceeds 1500

Deviation Variables u 1 and v 1 are called _____variables since they measure the amount by which the value produced by the solution deviates from the goal. Note that by definition, we want either u 1 or v 1 (or both) to be ______because it is impossible to simultaneously exceed and fall short of 1500. In order to make 12 x 1 + 29 x 2 as close as possible to 1500, it suffices to make the sum u 1 + v 1 small. The individual problem-solving condition is written as the goal ________: 19 x 1 + 11 x 2 + u 2 – v 2 = 2000 (u 2 > 0, v 2 > 0) As before, the sum of u 2 + v 2 should be_____.

The complete (______) model is: Min u 1 + v 1 + u 2 + v 2 s. t. x 1 + x 2 < 100 (total program hours) 12 x 1 + 29 x 2 + u 1 – v 1 = 1500 (small-group experience) 19 x 1 + 11 x 2 + u 2 – v 2 = 2000 (problem solving) x 1, x 2 , u 1, v 1, u 2, v 2 > 0 Note: Both u 1 and v 1 can’t be 0 Now this is an ____LP model and can be easily solved in Excel. The optimal decision variables will _______the system constraint (total program hours).

Solver will _____that either u 1 or v 1 (or both) will be zero, and thus these variables _______ satisfy this desired condition. The same statement holds for u 2 and v 2 and in general for any pair of ______variables. Note that the ______function is the sum of the deviation variables. This choice of an objective function indicates that there is no _____among the various deviations from the stated goals.

For example, any of the following three decisions is acceptable: 1. A decision that ________the group experience goal by 5 minutes and hits the problem-solving goal exactly, 2. A ______that hits the group experience goal exactly and underachieves the problemsolving goal by 5 minutes, and 3. A decision that _______each goal by 2. 5 minutes.

There is no ______among the following three solutions because each of these yields the same value (i. e. , 5) for the objective______. (1) u 1 = 0 v 1 = 5 u 2 = 0 v 2 = 0 (2) u 1 = 0 v 1 = 0 u 2 = 5 v 2 = 0 (3) u 1 = 2. 5 v 1 = 0 u 2 = 2. 5 v 2 = 0

Weighting the Deviation Variables Differences in units alone could produce a ______among the deviation variables. One way of expressing a preference among the various goals is to assign different ______ (weights) to the deviation variables in the objective function. In the program-planning example, one might select Min 10 u 1 + 2 v 1 + 20 u 2 + v 2 as the________. Since v 2 (over-achievement of problem solving) has the smallest coefficient, the program designers would rather have v 2 _____ than any of the other deviation variables (positive v 2 is _______the least).

With this objective function it is better to be 9 minutes over the problem-solving _______than to _______by 1 minute the small-groupexperience goal. To see this, note that for any solution in which u 1 > 1, decreasing u 1 by 1 and increasing v 2 by 9 would yield a smaller value for the objective function.

Goal Interval Constraints Another type of goal constraint is called a ________constraint. Such a constraint _____the goal to a range or interval rather than a specific ______value. Suppose, for example, that in the previous illustration the designers were ______among programs for which 1800 < [minutes of individual problem solving] < 2100 i. e. , 1800 < 19 x 1 + 11 x 2 < 2100 In this situation the interval goal is ______with two goal constraints: 19 x 1 + 11 x 2 – v 1 < 2100 (v 1 > 0) 19 x 1 + 11 x 2 + u 1 > 1800 (u 1 > 0)

When the terms u 1 and v 1 are included in the objective function, the LP ______will attempt to ______them. Summary of the Use of Goal Constraints Each goal constraint consists of a left-hand side, say gi(x 1, …, xn), and a right-hand side, bi. Goal constraints are written by using ______ deviation variables ui, vi. At optimality at least one of the pair ui, vi will always be____. ui represents underachievement; vi represents _______. Whenever ui is used it is ______to gi(x 1, …, xn). Whenever vi is used it is _______from gi(x 1, …, xn).

Only _____variables appear in the objective function, and the objective is always to______. The decision variables xi, i = 1, …, n do not appear in the_______. Four types of goals have been discussed: 1. ____. Make gi(x 1, …, xn) as close as possible to bi. To do this write the goal constraint as gi(x 1, …, xn) + ui - vi = bi (ui > 0, vi > 0)

2. _____Underachievement. To do this, write gi(x 1, …, xn) + ui - vi = bi (ui > 0, vi > 0) and in the_____, minimize ui, the underachievement. vi does not appear in the objective function and it is only in this_______, hence, the constraint can be equivalently written as gi(x 1, …, xn) + ui > bi (ui > 0) If the optimal ui is_____, this constraint will be active, for otherwise ui* could be made smaller. If ui*>0 then, since vi* must equal____, it must be true that gi(x 1, …, xn) + ui* = bi.

3. _____Overachievement. To do this, write gi(x 1, …, xn) + ui - vi = bi (ui > 0, vi > 0) and in the objective, minimize vi, the ______achievement. ui does not appear in the objective function, the constraint can be equivalently written as gi(x 1, …, xn) - vi < bi (vi > 0) If the optimal vi is_______, this constraint will be active. The argument is _____to that in item 2.

4. Goal Interval______. In this instance, the goal is to come as close as possible to satisfying ai < gi(x 1, …, xn) < bi In order to write this as a goal, first “____ out” the interval by writing ai - ui < gi(x 1, …, xn) < bi + vi (ui > 0, vi > 0) which is ______to the two constraints gi(x 1, …, xn) + ui > ai ^ gi(x 1, …, xn) + ui - vi + ai ^ (ui > 0, vi > 0) gi(x 1, …, xn) - ui > bi ^ gi(x 1, …, xn) + ui - vi + bi ^ (ui > 0, vi > 0) The objective function ui + vi is_______. ^ ^ Variables ui and vi are merely ______and slack, respectively.

ABSOLUTE PRIORITIES In some cases, managers do not wish to express their _____among various goals in terms of weighted deviation variables, for the process of assigning _____may seem too arbitrary or subjective. In such cases, it may be more acceptable to state preferences in terms of __________(as opposed to weights) to a set of goals. This approach requires that goals be ______in a specific order. Therefore, the model is solved in stages as a ______of models.

Example: Swenson’s Media Selection Model J. R. Swenson is an advertising agency which has just completed an agreement with a pharmaceutical manufacturer to mount a radio and television campaign to introduce a new product, Mylonal. The total expenditures for the campaign are not to exceed_______. The client wants to reach several audiences, however, radio and television are not equally ______in reaching all audiences. Therefore, the agency will estimate the _____of the advertisements in terms of rated exposures (i. e. , “people reached per month”) on the audiences of interest.

The following data represent the number of ______per $1000 expenditure: TV Total Upper Income RADIO 14, 000 1, 200 6, 000 1, 200 The following are the campaign goals, listed in order of absolute______. 1. Total exposures will hopefully be at least ______. 2. In order to maintain effective contact with the leading radio station, no more than _____ will be spent on TV advertising.

3. The campaign should achieve at least _______ upper-income exposures. 4. If all other goals are satisfied, the total number of exposures would come as close as possible to being______. Note that if all of the $120, 000 is spent on TV advertising, then the maximum _____ exposures would be 1, 680, 000 (120*14, 000). To model the problem, the following notation will be used: x 1 = dollars spent on _____( in thousands) x 2 = dollars spent on ______(in thousands) The objective function will be to maximize total ______and the other goals will be treated as ________.
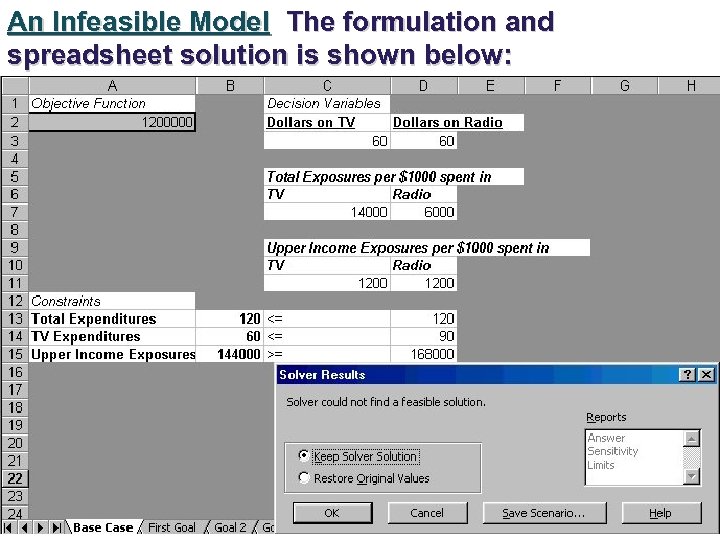
An Infeasible Model The formulation and spreadsheet solution is shown below:
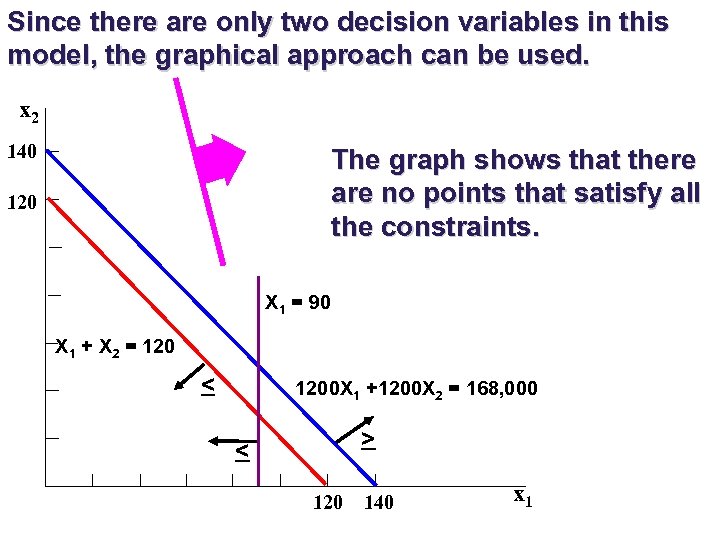
Since there are only two decision variables in this model, the graphical approach can be used. x 2 140 The graph shows that there are no points that satisfy all the constraints. 120 X 1 = 90 X 1 + X 2 = 120 < 1200 X 1 +1200 X 2 = 168, 000 > < 120 140 x 1

Swenson’s Goal Programming Model Note that the first goal (total exposures will be at least 840, 000), if violated, will be__________. The second goal (no more than $90, 000 will be spent on TV advertising), if violated, will be_______, etc. Employing this reasoning, the goals are restated, in _______priority, as: 1. ______the underachievement of 840, 000 total exposures. Min u 1 subject to the condition 14, 000 x 1 + 6, 000 x 2 + u 1 > 840, 000; u 1 > 0

2. Minimize _____in excess of $90, 000 on TV Min v 2 subject to the condition x 1 – v 2 < 90, 000; v 2 > 0 3. Minimize underachievement of 168, 000 upperincome______ Min u 3 subject to the condition 1, 200 x 1 + 1, 200 x 2 + u 3 > 168, 000; u 3 > 0 4. Minimize underachievement of 1, 680, 000 ____ exposures (the maximum possible) Min u 4 subject to the condition 14, 000 x 1 + 6, 000 x 2 + u 4 > 1, 680, 000; u 4 > 0

Note that the goals are now stated in terms of either _______underachievement (i. e. , min. ui) or minimizing _________(i. e. , min. vi). In addition, the goals have been expressed as _______. This method will facilitate a graphical analysis. Given that the priorities are formulated correctly, we must now distinguish between 1. _____constraints (all constraints that may not be violated) The only system constraint is: Total expenditures will be no _____than $120, 000 x 1 + x 2 < 120 2. _____constraints

The model can now be expressed as: Min P 1 u 1 + P 2 v 2 + P 3 u 3 + P 4 u 4 s. t. x 1 + x 2 < 120 14, 000 x 1 + 6, 000 x 2 + u 1 > 840, 000 x 1 - v 2 < 90 1, 200 x 1 + 1, 200 x 2 + u 3 > 168, 000 14, 000 x 1 + 6, 000 x 2 + u 4 > 1, 680, 000 x 1, x 2, u 1, v 2 , u 3, u 4 > 0 Note that the objective function consists only of _____variables and is of the ______form. In the objective function, P 1 denotes the highest _____, and so on. (S) (1) (2) (3) (4)

The previous problem statement precisely means: 1. Find the set of decision variables that satisfies the system _____(S) and that also gives the ____possible value to u 1 subject to constraint (1) and x 1, x 2, u 1 > 0. Call this set of decisions FR I (i. e. , feasible region I). Considering only the______, all of the points in FR I are “optimal” and (again considering only the highest goal), we are ______as to which of these points are selected.

2. Find the _______of points in FR I that gives the Min possible value to v 2, subject to constraint (2) and v 2 > 0. Call this subset FR II. Considering only the _____ranking of the two highest-priority goals, all of the points in FR II are “_______, ” and in terms of these two highest-priority goals, we are indifferent as to which of these points are selected. 3. Let FR III be the subset of points in FR II that _____u 3, subject to constraint (3) and u 3 > 0. 4. FR IV is the subset of points in FR III that minimize u 4, subject to ______(4) and u 4 > 0. Any point in FR IV is an optimal solution to the model.

Graphical Analysis and Spreadsheet Implementation of the Solution Procedure Since there are only two decision variables, we can use the ____method of LP. 1. Both the spreadsheet output and the _____reveal the Min of u 1 s. t. (S), (1), and x 1, x 2, u 1 > 0 is u 1* = 0. The important information is that u 1 = 0 which tells us that the first goal can be completely _____. Alternative _____for the current model are provided by all values of (x 1, x 2) that satisfy the conditions x 1 + x 2 < 120 FR I 14, 000 x 1 + 6, 000 x 2 > 840, 000 x 1, x 2 > 0
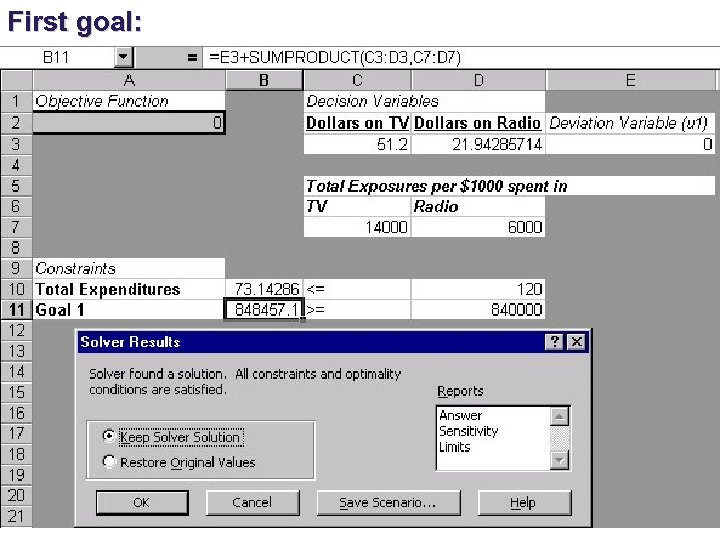
First goal:
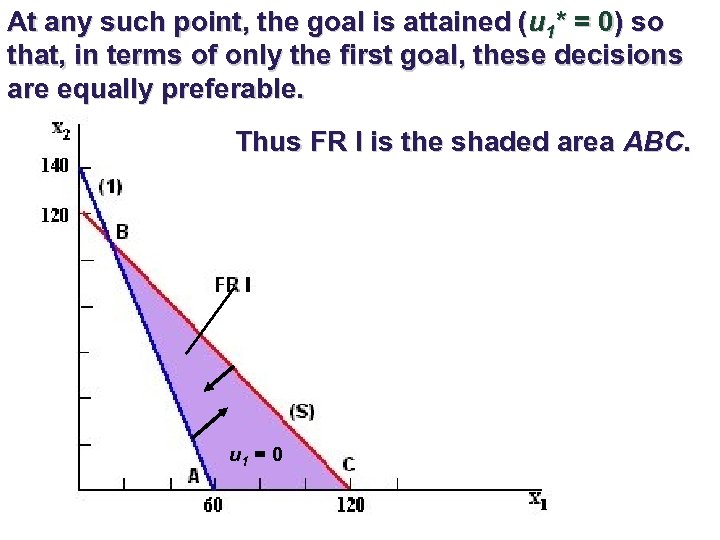
At any such point, the goal is attained (u 1* = 0) so that, in terms of only the first goal, these decisions are equally preferable. Thus FR I is the shaded area ABC. u 1 = 0
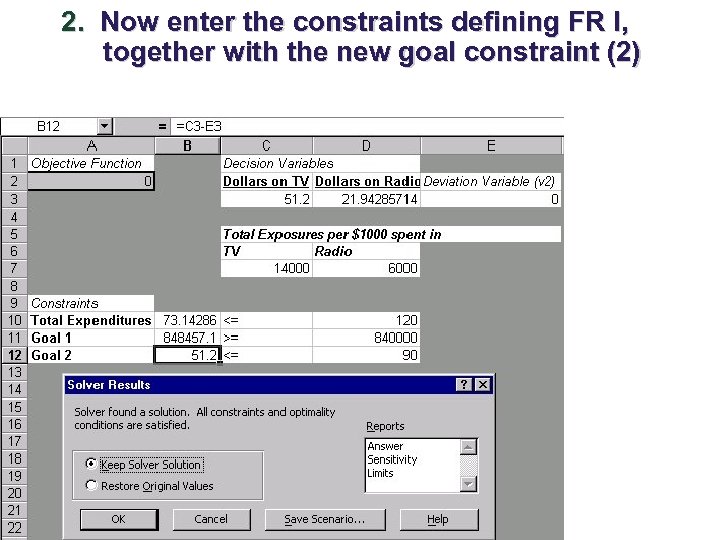
2. Now enter the constraints defining FR I, together with the new goal constraint (2)
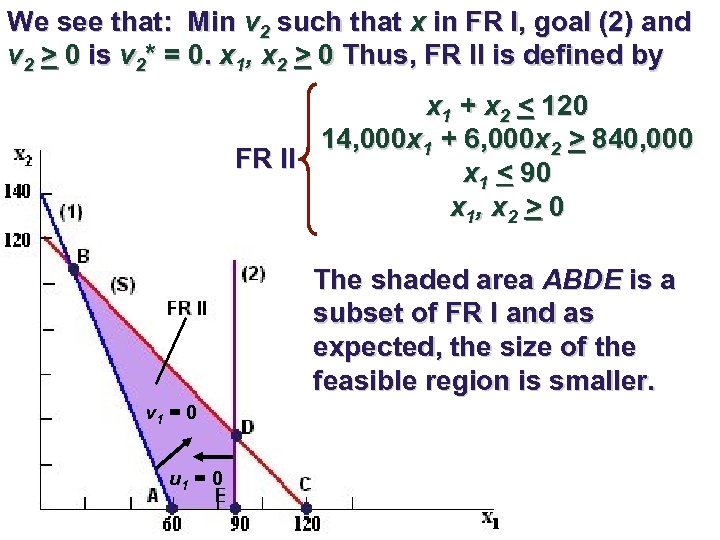
We see that: Min v 2 such that x in FR I, goal (2) and v 2 > 0 is v 2* = 0. x 1, x 2 > 0 Thus, FR II is defined by x 1 + x 2 < 120 14, 000 x 1 + 6, 000 x 2 > 840, 000 FR II x 1 < 90 x 1, x 2 > 0 The shaded area ABDE is a subset of FR I and as expected, the size of the feasible region is smaller. v 1 = 0 u 1 = 0
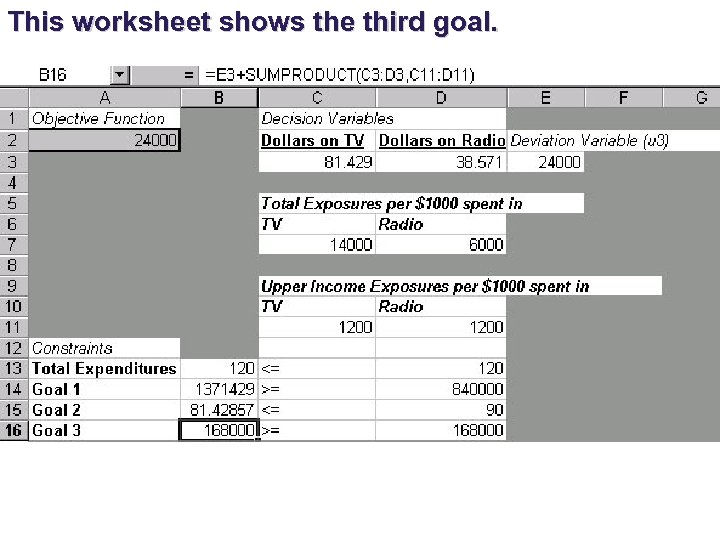
This worksheet shows the third goal.
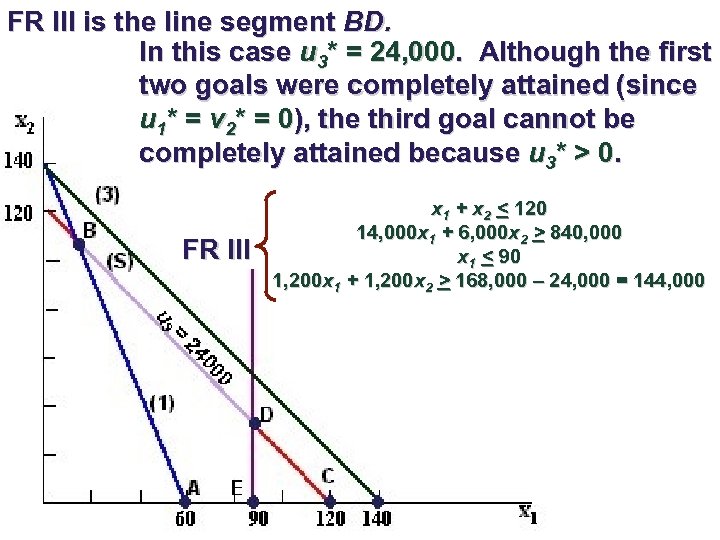
FR III is the line segment BD. In this case u 3* = 24, 000. Although the first two goals were completely attained (since u 1* = v 2* = 0), the third goal cannot be completely attained because u 3* > 0. FR III x 1 + x 2 < 120 14, 000 x 1 + 6, 000 x 2 > 840, 000 x 1 < 90 1, 200 x 1 + 1, 200 x 2 > 168, 000 – 24, 000 = 144, 000

The optimal solution is shown in this worksheet.

Recall that the fourth goal is to ______ underachievement of the maximum possible number of______, which is 1, 680, 000. Thus, we wish to minimize the underachievement u 4 where 14, 000 x 1 + 6, 000 x 2 + u 4 > 1, 680, 000 Since u 4 = 240, 000, we achieve 1, 680, 000 240, 000 = 1, 440, 000 exposures. The ______optimum is x 1* = 90, x 2* = 30 (i. e. , spend $90, 000 on TV ads & $30, 000 on radio ads).

COMBINING WEIGHTS AND ABSOLUTE PRIORITIES In reviewing the results of the _____priority study, the older members of the Mylonal market begins to take on importance. The exposures per $1000 of advertising are: EXPOSURE GROUP 50 and over TV RADIO 14, 000 6, 000 Note that radio and TV exposures are not equally _____in generating exposures in this segment of the population.

If there were no other considerations, then we would like as many _______exposures as possible. Since radio yields such exposures at a higher rate than TV (8000 > 3000), the maximum possible number of 50 -and-over exposures would be achieved by _____all of the $120, 000 available to radio. Thus, the maximum number of 50 -and-over exposures is 120 x 8000 = 960, 000. Once the first three goals are satisfied, we would like to come as close as possible to minimizing ____________. To resolve this conflict of goals, use a _____ sum of the deviation variables as the objective in the final ____of the absolute priorities approach.

It is decided that underachievement in the ____ (960, 000 exposures to the 50 -and-over group) is three times as _____as underachievement in the fourth goal (1, 680, 000 total exposures).
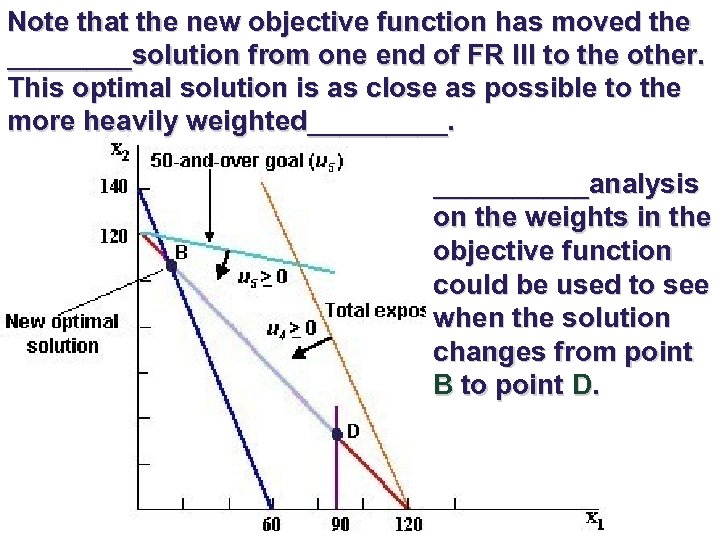
Note that the new objective function has moved the ____solution from one end of FR III to the other. This optimal solution is as close as possible to the more heavily weighted_____analysis on the weights in the objective function could be used to see when the solution changes from point B to point D.

ANALYTICAL HIERARCHY PROCESS This section deals with the real-world topic of making a decision when there are ____ objectives or criteria to consider. For example: Choosing which employment offer to accept. Picking which computer (or car, etc. ) to buy. Deciding which new product to launch first. Selecting a site for a new restaurant, hotel, etc. Rating the best cities in which to live. Choosing a new software package for your company.

A simple way to attack such a decision would be to assign _____to each of the criteria that were to be considered in making the decision. Then, _____each decision alternative on a scale from 1 (worst) to 10 (best). Finally, you would _____the weights times the rankings for each criterion and sum them up. The ______with the highest score would be the most preferred.

For example, you are in charge of purchasing the next computer for the office. You have to choose between the following three computers: 1. Model A runs an AMD K 6 -II chip at 400 MHz 2. Model B runs a Celeron chip at 333 MHz 3. Model C runs a Pentium II chip at 450 MHz The important criteria and their weights are: Criteria Price Speed Hard-disk Size Warranty/Support Weight 50% 15% 20% 15%

Now, rank each of the three models on these four _______. Rank them on a scale from 1 to 10 as described earlier. Model B has the highest weighted _______and thus would be the best computer to purchase.

This approach is quite ______and there are difficulties in setting the ranking scales on such different criteria. Analytic hierarchy process (AHP) also uses a weighted ____approach idea, but it uses a method for assigning ratings (or rankings) and weights that is considered more ______and consistent. (AHP) is based on ____comparisons between the decision alternatives on each of the criteria. Then, a similar set of _______are made to determine the relative importance of each criterion and thus produces the______.

The basic procedure is as follows: 1. Develop the _____for each decision alternative for each criterion by • developing a pairwise comparison _____ for each criterion • _____the resulting matrix • _____the values in each row to get the corresponding rating • calculating and checking the _____ ratio

2. Develop the ____for the criteria by • developing a pairwise comparison matrix for each______ • normalizing the _____matrix • averaging the values in each _____to get the corresponding rating • calculating and ____the consistency ratio 3. Calculate the _______average rating for each decision alternative. Choose the one with the _____score.

Consider the following example: Sleepwell Hotels is looking for some help in selecting the “best” revenue management software package from among several vendors. The director of revenue management for this chain of hotels has been given this task. Three vendors have been identified whose software meets the following basic needs: Revenue Technology Corporation (RTC) PRAISE Strategic Solutions (PSS) El Cheapo (EC)
The important criteria are: 1. The ______of the installed system 2. The follow-up _____provided over the coming year 3. The sophistication of the ______math engines 4. The amount of _______for Sleepwell

The first step in the AHP procedure is to make pairwise ______between the vendors for each criterion. Here is the ____scale for making these comparisons: RATING 1 3 5 7 9 DESCRIPTION Equally preferred Moderately preferred Strongly preferred Very strongly preferred Extremely strongly preferred Values 2, 4, 6, or 8 may also be assigned and represent ______halfway between the integers on either side.

Start with the total cost _____and generate the following data in a spreadsheet: The _______in the row is being compared to the vendor in the column. A value between 1 and 9 indicates that the vendor in the row is _____to the vendor in the column. If the vendor in the ______is preferred to the vendor in the row, then the inverse of the rating is given.
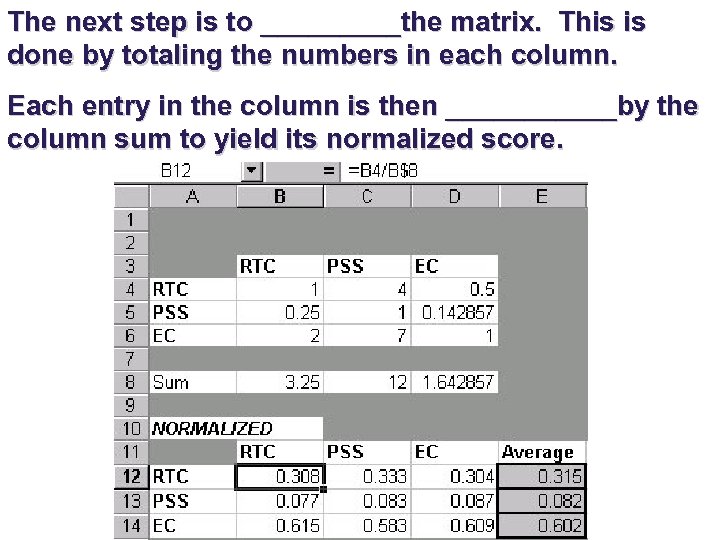
The next step is to _____the matrix. This is done by totaling the numbers in each column. Each entry in the column is then ______by the column sum to yield its normalized score.

Now, calculate the _________and check its value. The purpose for doing this is to make sure that the original preference ratings were_____. There are 3 steps to arrive at the consistency ratio: 1. Calculate the consistency ____for each vendor. 2. Calculate the consistency ____(CI). 3. Calculate the consistency ____(CI/RI where RI is a random index). To calculate the consistency measure, we can take advantage of Excel’s matrix _______function =MMULT().

Multiply the average ______for each vendor times the scores in the first row one-at-a-time, sum these products up and divide this _____by the average rating for the first vendor.

N RANDOM INDEX 2 3 4 5 6 7 8 9 10 0. 00 0. 58 0. 90 1. 12 1. 24 1. 32 1. 41 1. 45 1. 51

If we are perfectly______, then the consistency measures will equal n and therefore, the CIs will be equal to ______and so will the consistency_______. If this ratio is very ____(Saaty suggests > 0. 10), then we are not consistent enough and the best thing to do is go back and _______the comparisons. Now, continue for the other three criteria. You can easily do this by copying the “____” sheet into three other sheets (“Service, ” “Sophistication, ” and “Custom”) and then simply changing the _______ comparisons.

Consistency ratio for “Service. ”

Consistency ratio for “Sophistication. ”
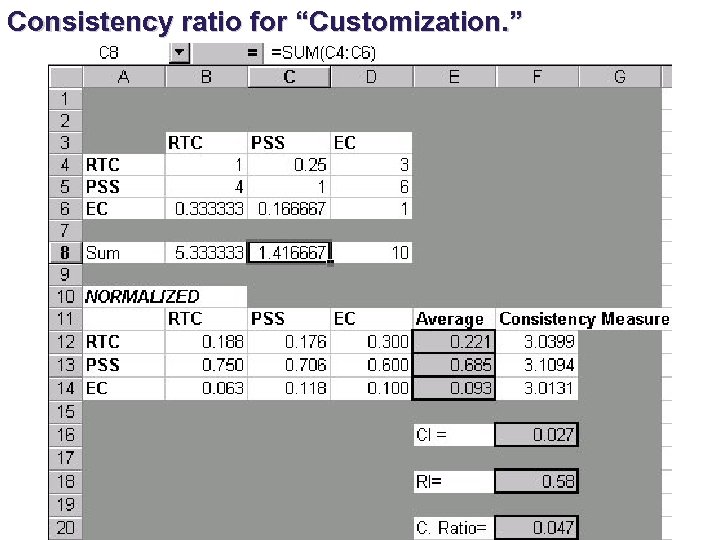
Consistency ratio for “Customization. ”

In all three cases, the CR value ranges from 0. 0 to 0. 047 which means that we are being______. Note also that PSS is the winner on the Service criterion, RTC and PSS are tied for the best in terms of Sophistication, and PSS is considered the best on Customization. All of this work concludes the first step in the procedure. The next step is to use similar ______ comparisons to determine the appropriate _______ for each of the criteria. The process is the same in that we make _______, except that now we make the comparisons between the criteria not the vendors.
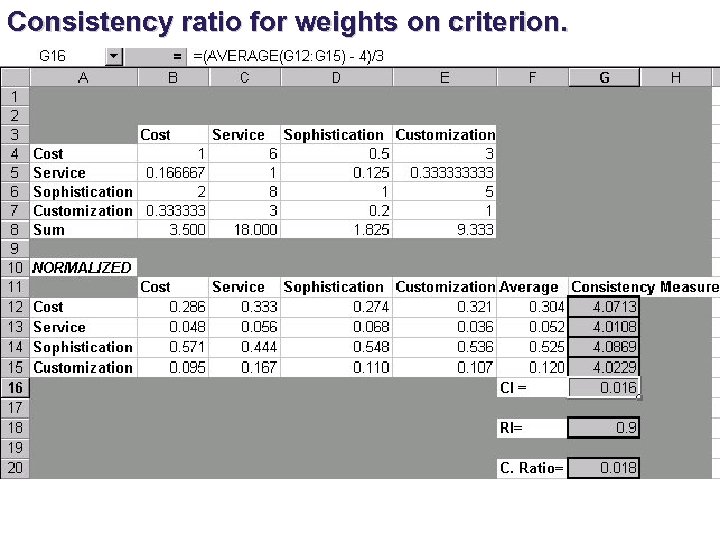
Consistency ratio for weights on criterion.
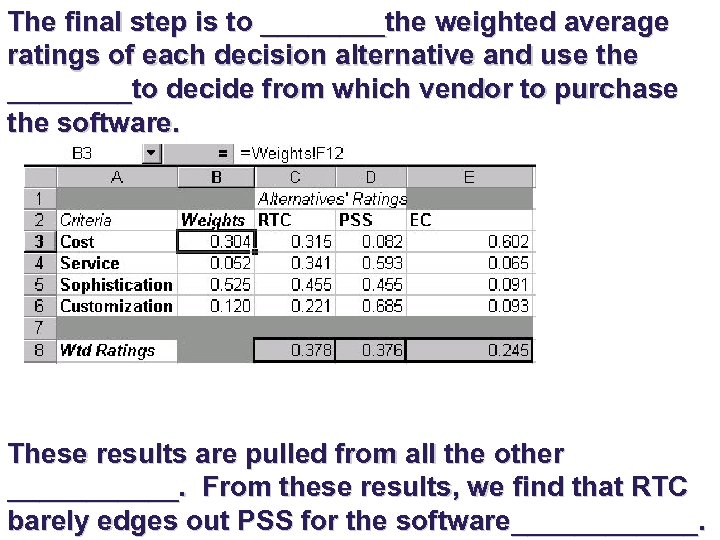
The final step is to ____the weighted average ratings of each decision alternative and use the ____to decide from which vendor to purchase the software. These results are pulled from all the other ______. From these results, we find that RTC barely edges out PSS for the software______.
25cbb439576137efcb5f4dc1e0e7b041.ppt