Decision making under uncertainty is hard Reasoning

Decision making under uncertainty is hard.

Reasoning under uncertainty. There are two ways to do it

Observational Inference Causal Inference

The Bayesian Networks or Bayesian Belief Networks, an important subset of Bayesian statistics, are based on the Definition A Bayesian Network models a decision problem by mapping out cause-and-effect relationships among key variables and assigning to them probabilities that represent the extent to which one variable is likely to affect another. idea of the degree of belief and causality. Let’s use an illustration to understand this concept.

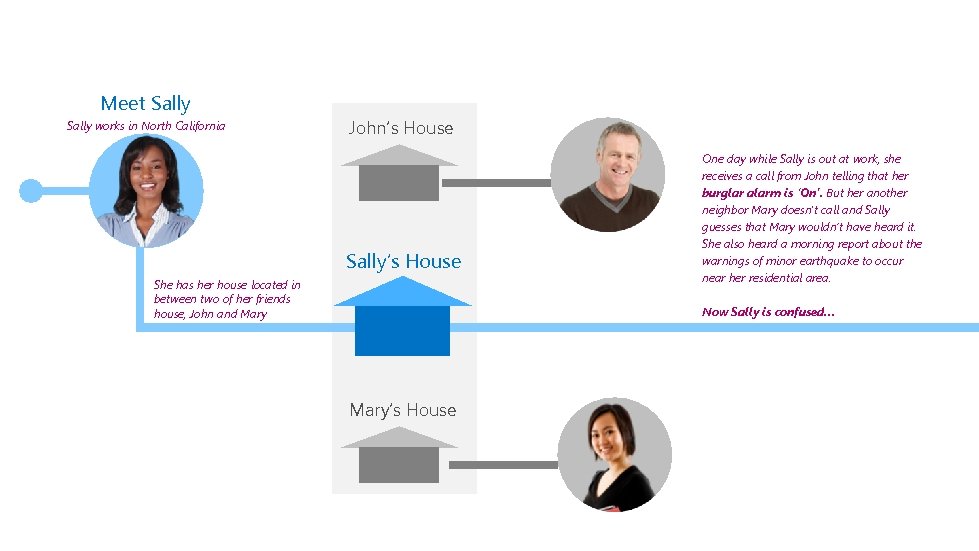Meet Sally works in North California John’s House Sally’s House She has her house located in between two of her friends house, John and Mary One day while Sally is out at work, she receives a call from John telling that her burglar alarm is ‘On’. But her another neighbor Mary doesn't call and Sally guesses that Mary wouldn’t have heard it. She also heard a morning report about the warnings of minor earthquake to occur near her residential area. Now Sally is confused… Mary’s House

1. “Did Mary not hear the alarm at all” OR 2. “Did the alarm rang and stopped due to earthquake due to loose connections” OR 3. “Is there really a burglar as alarm is on? AND Sally’s observed/ heard facts has affected your belief/reasoning, that “Is there a burglar or not? ” 4. The Burglar could have set it off himself ? Let’s understand how a Bayesian network model can help us reason under uncertainty.

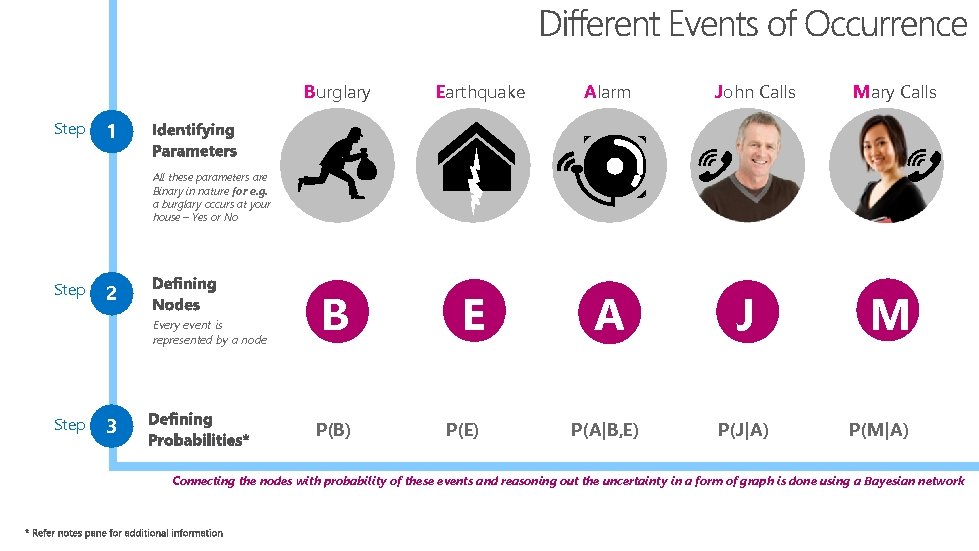Burglary Step Earthquake Alarm John Calls Mary Calls 1 All these parameters are Binary in nature for e. g. a burglary occurs at your house – Yes or No Step 2 Step 3 B E P(B) Every event is represented by a node P(E) A J P(A|B, E) P(J|A) M P(M|A) Connecting the nodes with probability of these events and reasoning out the uncertainty in a form of graph is done using a Bayesian network

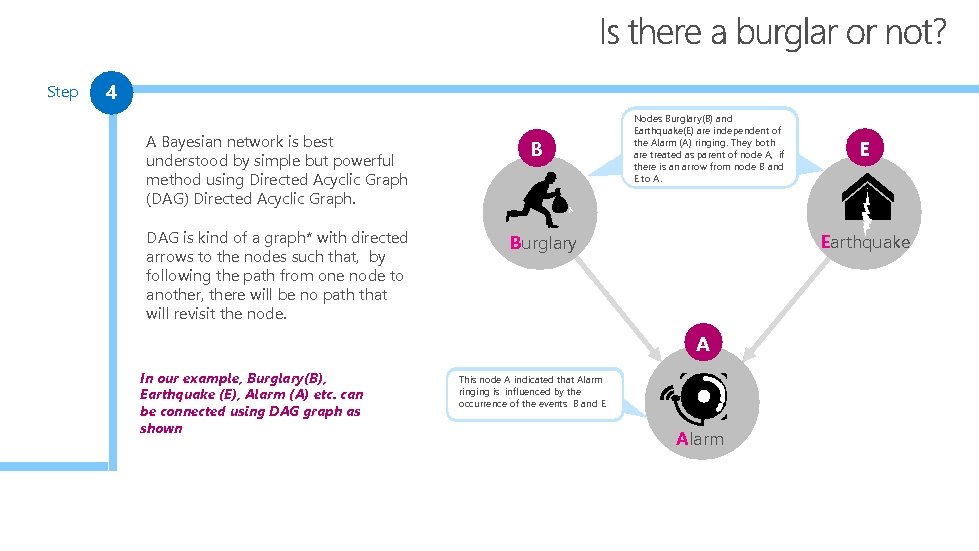Step 4 A Bayesian network is best understood by simple but powerful method using Directed Acyclic Graph (DAG) Directed Acyclic Graph. DAG is kind of a graph* with directed arrows to the nodes such that, by following the path from one node to another, there will be no path that will revisit the node. B Nodes Burglary(B) and Earthquake(E) are independent of the Alarm (A) ringing. They both are as parent of node A, are treated as parent of if node an arrow is an arrow there is. A, if therefrom node B and E to A. Earthquake Burglary A In our example, Burglary(B), Earthquake (E), Alarm (A) etc. can be connected using DAG graph as shown E This node A indicated that Alarm ringing is influenced by the occurrence of the events B and E Alarm

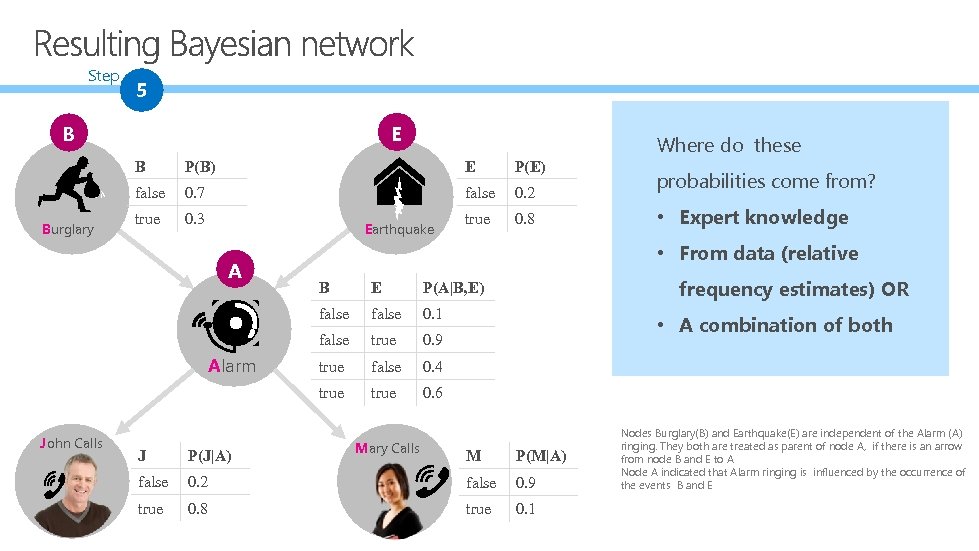Step 5 B E Where do these B E P(E) false Burglary P(B) 0. 7 false 0. 2 true 0. 3 true 0. 8 Earthquake A P(J|A) false true E false 0. 1 true 0. 9 true false 0. 4 true frequency estimates) OR P(A|B, E) true J B false John Calls • Expert knowledge • From data (relative false Alarm probabilities come from? 0. 6 Mary Calls • A combination of both M P(M|A) 0. 2 false 0. 9 0. 8 true 0. 1 Nodes Burglary(B) and Earthquake(E) are independent of the Alarm (A) ringing. They both are treated as parent of node A, if there is an arrow from node B and E to A Node A indicated that Alarm ringing is influenced by the occurrence of the events B and E

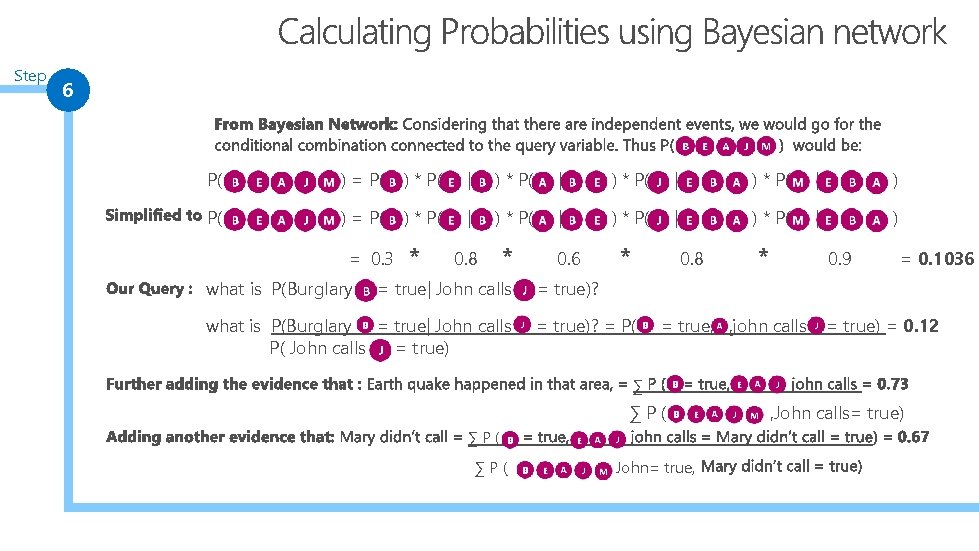Step 6 P( ) = P( ) * P( | ) * P( | ) = 0. 3 what is P(Burglary * 0. 8 * = true| John calls what is P(Burglary = true| John calls P( John calls = true) * 0. 6 0. 8 * 0. 9 = 0. 1036 = true)? = P( = true, , john calls = true) = 0. 12 ∑ ∑P( ∑P( , John= true, , John calls= true)

Step 7 The probability of burglary is 67% based on available evidence so far, however, adding more evidences the probability becomes more accurate and closer to the real scenario

The basic concept behind Bayesian networks is the computation of every node’s belief (conditional probability) given the evidence is observed Many intelligent systems (e. g. feed forward neural networks, fuzzy logic) are strictly one-way in the sense that when a model is given a set of inputs it can predict the output, but not vice versa. Bayesian networks can do ‘bi-directional modelling within a single structure’ because variables are not specified as being solely for input or for output. By applying Bayes’ theorem, the direction of the relationship can be reversed. Bayesian networks can provide Predictive Inference and Diagnostic reasoning Cause Predictive Inference For example, given the rule "If (product is sweet) then (product is preferred)" and given the fact "product is sweet“ we can obviously deduce that it is preferred. However, with a Bayesian system, we might observe (or hypothesise) that "product is preferred" and deduce that this preference must be caused by its sweetness, i. e. that "product is sweet". In other words, Many systems can perform induction, Bayesian networks can also perform abduction. Effect Cause Diagnostic Reasoning Effect

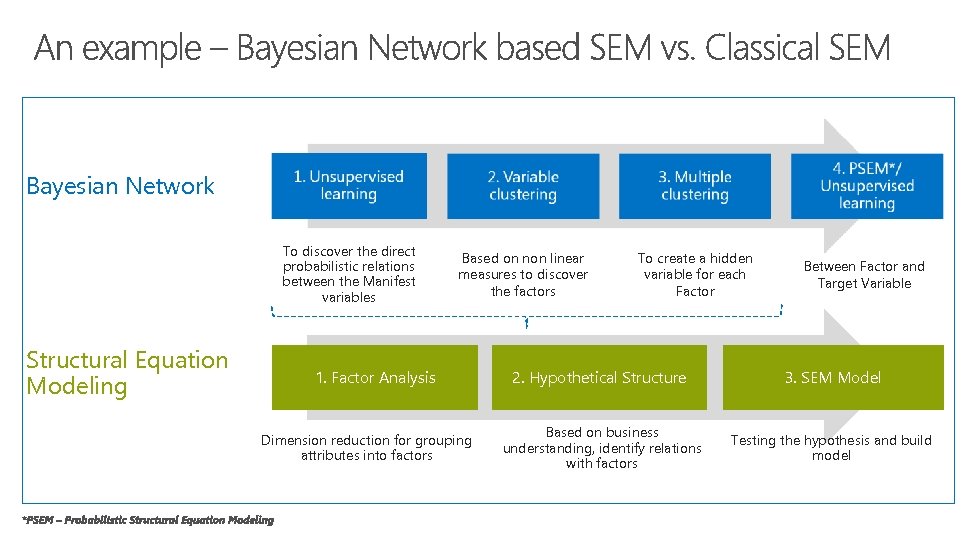Bayesian Network To discover the direct probabilistic relations between the Manifest variables Structural Equation Modeling Based on non linear measures to discover the factors 1. Factor Analysis Dimension reduction for grouping attributes into factors To create a hidden variable for each Factor Between Factor and Target Variable 2. Hypothetical Structure 3. SEM Model Based on business understanding, identify relations with factors Testing the hypothesis and build model

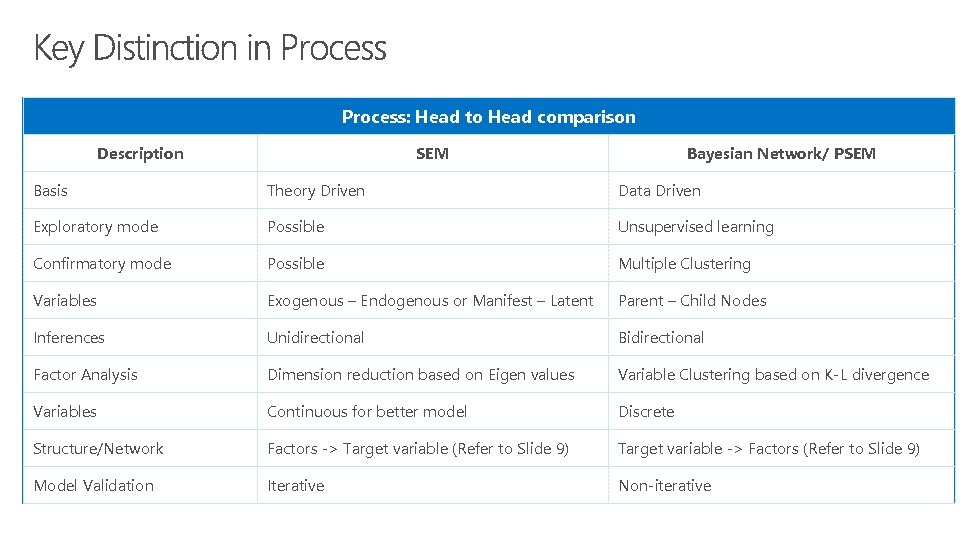Process: Head to Head comparison Description SEM Bayesian Network/ PSEM Basis Theory Driven Data Driven Exploratory mode Possible Unsupervised learning Confirmatory mode Possible Multiple Clustering Variables Exogenous – Endogenous or Manifest – Latent Parent – Child Nodes Inferences Unidirectional Bidirectional Factor Analysis Dimension reduction based on Eigen values Variable Clustering based on K-L divergence Variables Continuous for better model Discrete Structure/Network Factors -> Target variable (Refer to Slide 9) Target variable -> Factors (Refer to Slide 9) Model Validation Iterative Non-iterative

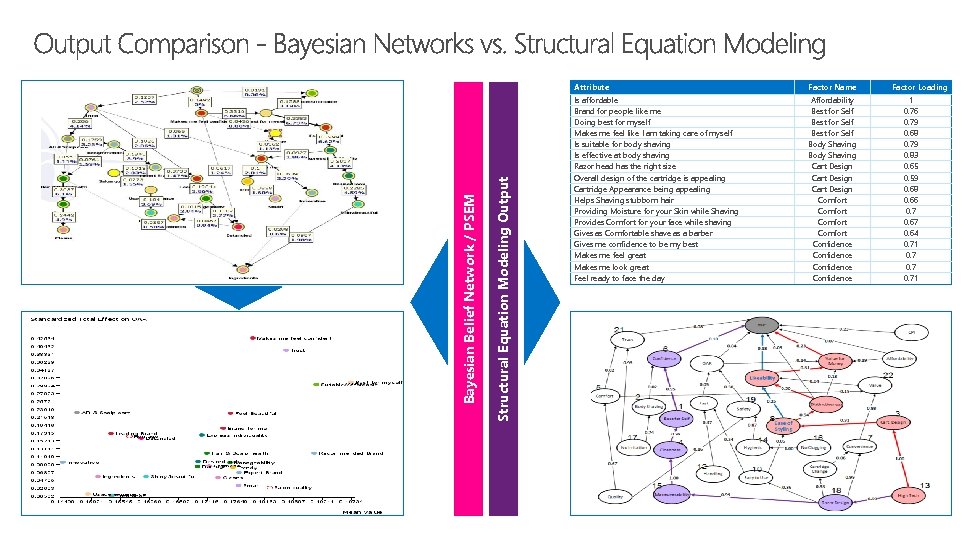Structural Equation Modeling Output Bayesian Belief Network / PSEM Attribute Factor Name Is affordable Brand for people like me Doing best for myself Makes me feel like I am taking care of myself Is suitable for body shaving Is effective at body shaving Razor head has the right size Overall design of the cartridge is appealing Cartridge Appearance being appealing Helps Shaving stubborn hair Providing Moisture for your Skin while Shaving Provides Comfort for your face while shaving Gives as Comfortable shave as a barber Gives me confidence to be my best Makes me feel great Makes me look great Feel ready to face the day Affordability Best for Self Body Shaving Cart Design Comfort Confidence Factor Loading 1 0. 76 0. 79 0. 68 0. 79 0. 83 0. 65 0. 59 0. 68 0. 66 0. 7 0. 64 0. 71 0. 71

Within market research, we can use it to model data related to: § Customer behavior chain, § Satisfaction questionnaire analysis, § Customer and product segmentation § Purchase Intent to the product § Customer Satisfaction Sector specific use cases: § CPG & Retail: • Marketing Mix Modeling • Price Optimization § Technology: • ROI & Sales Drivers § Telecom & Banking: • Churn Analysis & Propensity modeling

Security and Fraud Detection: Bayesian methods provide a method of detecting credit card fraud. The way in which a stolen credit card is used will be different to its normal use, but spending patterns can also change for legitimate reasons. Bayes‘ Theorem is crucial in assessing the likelihood of fraud given the spending patterns. AT&T developed a similar system to detect telephone fraud. Again, patterns of behaviour are sought, in this case calls to a previously Objective: To assess probability the credit card used by fraud given that the person spending pattern Here, Query variable is fraud detection and Evidence variable is abnormal use or spending pattern. Telecommunications provider is losing out too many customers to its competitors (churn): Here, Bayesian model can be build used on an existing month’s churn data to predict which customers may be likely to churn in the future. Further adding the following month’s data the model can be refined and retrained using Network learning method. Why Bayesian Network: It is the process of updating probabilities of outcomes based upon the relationships in the model and the evidence known about the situation at hand. It is an assimilation of Bayesian Network, Machine Learning & Information Theory – a complete contrast to standard statistical modeling Medicine Speech recognition Stock market Text Classification Bio-informatics Computer troubleshooting

Microsoft’s OFFICE ASSISTANT is an application of Bayesian inference techniques. The OFFICE ASSISTANT was based on prototypes developed within the LUMIÈRE Project (Horvitz et al. 1998; Lumiere 1998). The approach taken is to develop Bayesian user models that capture the uncertain relationships among the goals and needs of a user and observations about program state, sequences of actions over time, and words in a user’s query. The US Navy have developed real-time software for determining the performance of various ship self-defence weapon systems against varying types and ranges of incoming attack weapons. NASA’s Mission Control Centre in Houston use Bayesian Networks to interpret live telemetry and provide advice on the likelihood of failures of the space shuttle's propulsion systems. Intel uses Bayesian Networks for diagnosis of faults in processor chips. Given end-of-line tests on semiconductor chips, a statistical process can be used to infer possible processing problems. Nokia Networks uses the Hugin Decision Engine, a commercial tool making use of Bayesian Networks, in a prototype tool for efficient diagnosis of problems with mobile networks. By having an automated tool that reads network performance data and from that estimates and monitors network problems ranked by probability, the network operator gets an efficient troubleshooting procedure saving both expensive expert resources and downtime of the network.

Contact: aaa@bbb. com ppp@qqq. com xxx@yyy. com